机器学习第7天:逻辑回归
文章目录
介绍
概率计算
逻辑回归的损失函数
单个实例的成本函数
整个训练集的成本函数
鸢尾花数据集上的逻辑回归
Softmax回归
Softmax回归数学公式
Softmax回归损失函数
调用代码
参数说明
结语
介绍
作用:使用回归算法进行分类任务
思想:将回归值转为概率值,然后找到一个适当的数值,当概率大于这个值时,归为一类,当小于这个值时,归为另一类
概率计算
函数的输入值为特征的加权和
是sigmoid函数,公式为
函数图像为

可见它输出一个0-1的值,我们可以将这个值当作概率
则我们可以通过这个概率来分类,设定一个值,在这个值的两端进行分类
逻辑回归的损失函数
单个实例的成本函数
当p>=0.5时
当p<0.5时
整个训练集的成本函数
这个损失函数也是一个凸函数,可以使用梯度下降法使损失最小化
鸢尾花数据集上的逻辑回归
鸢尾花数据集是机器学习中一个经典的数据集,它有花瓣和花萼的长和宽,任务是用它们来判断鸢尾花的种类
看代码和效果
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
import numpy as npiris = datasets.load_iris()x = iris["data"][:, 3:]
y = (iris["target"] == 2)model = LogisticRegression()
model.fit(x, y)x_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = model.predict_proba(x_new)
plt.plot(x_new, y_proba[:, 1], "g-", label="Iris virginica")
plt.plot(x_new, y_proba[:, 0], "b--", label="Not Iris virginica")plt.xlabel("Petal width")
plt.ylabel("probability")plt.legend()
plt.show()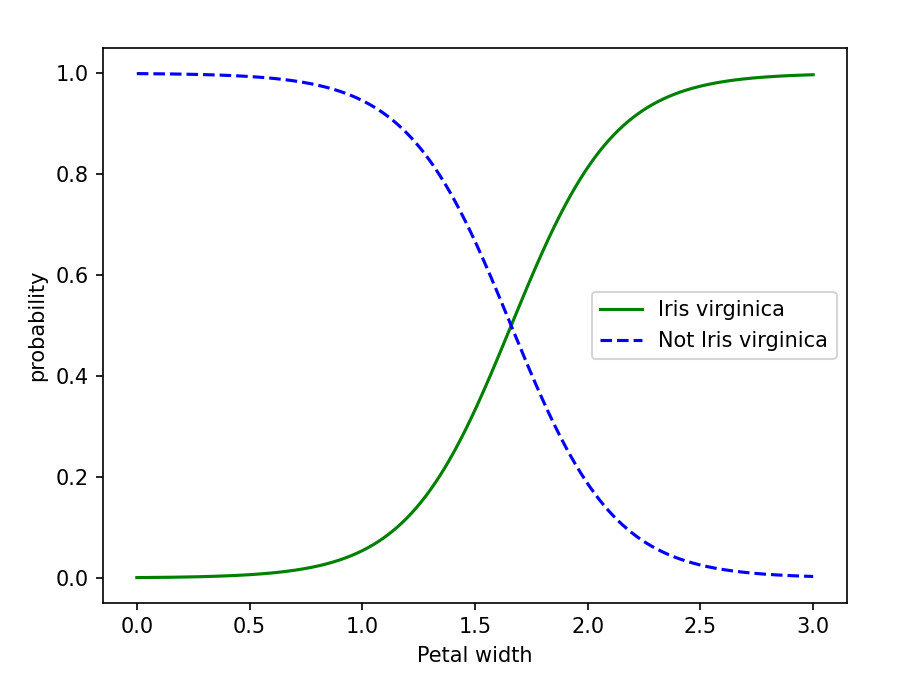
可以看见,当花瓣长度变化的时候,两种花种类的概率随之变化
简单介绍一下新的代码,predict.proba方法返回样本为可能的两种花的概率。
Softmax回归
上述方法主要用于二分类任务,我们再来看一种多分类方法,Softmax回归
Softmax回归数学公式
Softmax函数也叫指数归一化函数,它对x进行指数处理再进行归一化得出一个概率
这个函数的自变量为一个分数s,这个s由我们的数据的转置矩阵与一个参数相乘得来
对于不同的类,参数都不相同,模型训练的任务就是拟合这个参数
Softmax回归损失函数
当k=2时(二分类),此成本函数等于sigmoid逻辑回归的成本函数
调用代码
model = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10)
model.fit(x, y)参数说明
multi_class="multinomial": 表示采用多类别分类,即多类别的逻辑回归问题,与二元逻辑回归不同。
solver="lbfgs": 表示使用LBFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)优化算法进行求解。
C=10: 表示正则化参数,控制模型的正则化强度,C值越小,正则化强度越高。
结语
逻辑回归是一种简单的分类方法,二分类任务就用第一种方法,多分类任务就用第二种方法
相关文章:
机器学习第7天:逻辑回归
文章目录 介绍 概率计算 逻辑回归的损失函数 单个实例的成本函数 整个训练集的成本函数 鸢尾花数据集上的逻辑回归 Softmax回归 Softmax回归数学公式 Softmax回归损失函数 调用代码 参数说明 结语 介绍 作用:使用回归算法进行分类任务 思想:…...

努力奋斗,遇上对的人
...

基于单片机音乐弹奏播放DS1302万年历显示及源程序
一、系统方案 1、本设计采用51单片机作为主控器。 2、DS1302计时显示年月日时分秒。 3、按键可以弹奏以及播放音乐,内置16首音乐。 二、硬件设计 原理图如下: 三、单片机软件设计 1、首先是系统初始化 /时钟显示**/ void init_1602_ds1302() { write…...

ceph学习笔记
ceph ceph osd lspoolsrbd ls -p testpool#查看 ceph 集群中有多少个 pool,并且每个 pool 容量及利 用情况 rados dfceph -sceph osd tree ceph dfceph versionsceph osd pool lsceph osd crush rule dumpceph auth print-key client.adminceph orch host lsceph crash lsceph…...
SQLSERVER 遍历循环的两种方式很详细有源码(2)
2.游标循环 Create table WS_Student ( [Id] int primary key not null, [My_Cocode] [int], [My_SCocode] [int], [userId] [bigint], [SetCName] [varchar](50) NULL, [SetEName] [varchar](50) NULL, [SetPcode] [varchar](50) NULL, [Se…...

flutter背景图片设置
本地图片设置 1、在配置文件pubspec.yaml中,设置以下代码 assets:- assets/- assets/test/2、如果目录中没有assets文件夹,则创建一个文件夹,并且取名为assets,在此文件夹中存放图片资源即可,如果想分文件夹管理&…...
【运维 监控】Grafana + Prometheus,监控Linux
安装和配置Grafana与Prometheus需要一些步骤,下面是一个简单的指南: 安装 Prometheus: 使用包管理器安装 Prometheus。在 Debian/Ubuntu 上,可以使用以下命令: sudo apt-get update sudo apt-get install prometheus在…...
Sentinel底层原理(下)
1、概述 Sentinel的核心原理,也就是前面提到暗流涌动的SphU.entry(…)这行代码背后的逻辑。 Sentinel会为每个资源创建一个处理链条,就是一个责任链,第一次访问这个资源的时候创建,之后就一直复用,所以这个处理链条每…...
竞赛选题 疫情数据分析与3D可视化 - python 大数据
文章目录 0 前言1 课题背景2 实现效果3 设计原理4 部分代码5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 大数据全国疫情数据分析与3D可视化 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐࿰…...

macos 配置ndk环境
选择Android Studio下默认的ndk环境 mac电脑的ndk默认路径一般是 /Users/user_name/Library/Android/sdk/ndk/version_code 其中user_name为自己电脑的用户名,version_code为自己ndk安装的版本号,比如我这里电脑的ndk路径就是 /Users/zhangsan/Libra…...
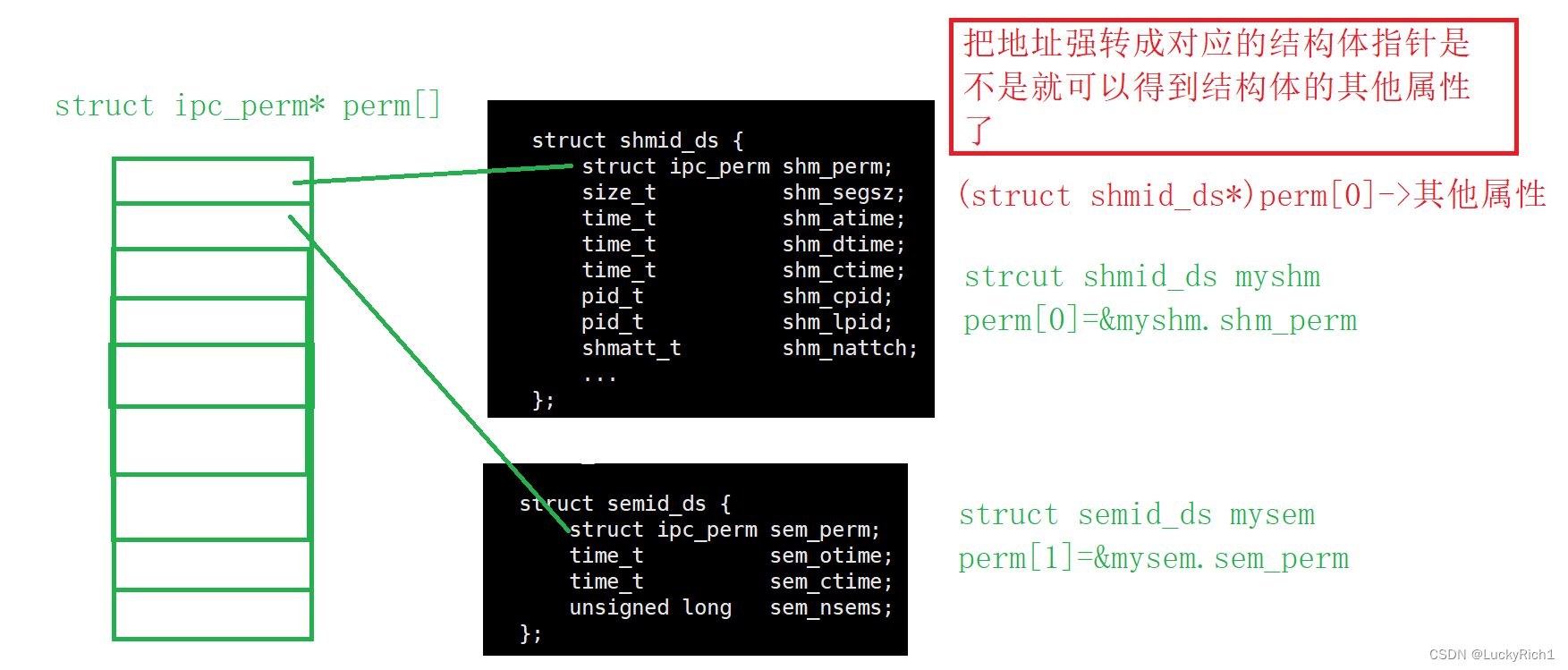
【linux】进行间通信——共享内存+消息队列+信号量
共享内存消息队列信号量 1.共享内存1.1共享内存的原理1.2共享内存的概念1.3接口的认识1.4实操comm.hppservice.cc (写)clint.cc (读) 1.5共享内存的总结1.6共享内存的内核结构 2.消息队列2.1原理2.2接口 3.信号量3.1信号量是什么3…...
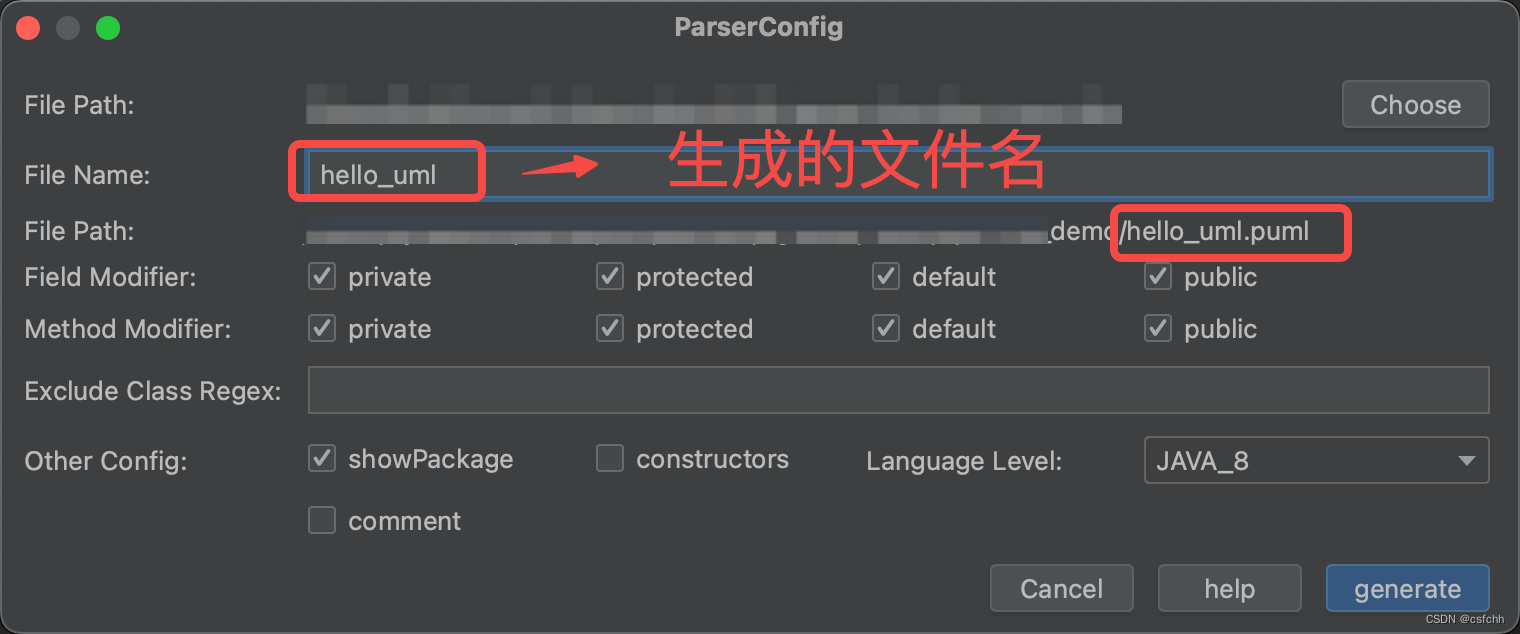
PlantUML基础使用教程
环境搭建 IDEA插件下载 打开IEDA系列IDE,从FIle–>Settings–>Plugins–>Marketplace 进入到插件下载界面,搜索PlantUML,安装PlantUML Integration和PlantUML Parser两个插件,并重启IDE 安装和配置Graphviz 进入官网…...

Redis:新的3种数据类型Bitmaps、HyperLoglog、Geographic
目录 Bitmaps简介常用命令bitmaps与set比较 HyperLoglog简介命令 Geographic简介命令 Bitmaps 简介 位操作字符串。 现代计算机使用二进制(位)作为信息的基本单位,1个字节等于8位,例如“abc”字符串是有3个字节组成,…...

promise时效架构升级方案的实施及落地 | 京东物流技术团队
一、项目背景 为什么需要架构升级 promise时效包含两个子系统:内核时效计算系统(系统核心是时效计算)和组件化时效系统(系统核心是复杂业务处理以及多种时效业务聚合,承接结算下单黄金流程流量)ÿ…...

es的使用方法以及概念
Elasticsearch(简称为ES)是一个开源的搜索引擎,它构建在Lucene搜索引擎之上。它提供了一个分布式、多租户的全文搜索引擎,具有强大的实时分析能力。以下是关于Elasticsearch的一些基本概念和使用方法: 基本概念&#…...
WPF xaml Command用法介绍
WPF (Windows Presentation Foundation) 中的命令设计模式是一种用于分离用户界面逻辑和业务逻辑的方法。在WPF中,这种模式通过命令接口(如 ICommand)实现,使得用户界面组件(如按钮、菜单项等)可以触发不直…...

微信小程序动态生成表单来啦!你再也不需要手写表单了!
dc-vant-form 由于我们在小程序上涉及到数据采集业务,需要经常使用表单,微信小程序的表单使用起来非常麻烦,数据和表单是分离的,每个输入框都需要做数据处理才能实现响应式数据,所以我开发了dc-vant-form,…...

顺序表(数据结构与算法)
✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅ ✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨ 🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿…...

【大连民族大学C语言CG题库练习题】——判断一个矩阵是另一个矩阵的子矩阵
【问题描述】 从标准输入中输入一个N(N<9)阶矩阵和一个M(M<N)阶矩阵,判断矩阵M是否是N的子矩阵,若是则输出M在N中的起始位置,若不是则输出-1。若矩阵M能与N中某一区域完全相等࿰…...

C#WPF控制模板实例
一、控制模板 ControlTemplate(控件模板)不仅是用于来定义控件的外观、样式, 还可通过控件模板的触发器(ControlTemplate.Triggers)修改控件的行为、响应动画等。 控件模板定义控件的视觉外观,所有的 UI 元素都具有某种外观和行为,例如,Button 具有外观和行为。单击事件或…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
