LeetCode算法题解(动态规划)|LeetCode509. 斐波那契数、LeetCode70. 爬楼梯、LeetCode746. 使用最小花费爬楼梯
一、LeetCode509. 斐波那契数
题目链接:509. 斐波那契数
题目描述:
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
算法分析:
根据动规五部曲来就可以了。
这道题题目已经给了我们地推的公式F[n]=F[n-1]+F[n-2],以及其初始值F[0]=1,F[1]=1,所以我们只需要明白F[n]及其下标的含义就可以了。
显然F[n]表示数列中第n项数的值。
然后我们来遍历整个数组,按照递推公式依次确定每个项的值。
最后返回第n项F[n]即可。
如果算出来的结果有问题,可以把数组打印出来,检查递推是否有问题。
代码如下:
class Solution {public int fib(int n) {if(n <= 1) return n;int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for(int i = 2; i <= n; i++)dp[i] = dp[i - 1] + dp[i - 2];return dp[n];}
}时间复杂度o(n)空间复杂度o(n).
二、LeetCode70. 爬楼梯
题目链接:70. 爬楼梯
题目描述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
提示:
1 <= n <= 45
算法分析:
确定dp数组及下标含义:
用dp[i]表示爬到第i阶楼梯可以有多少种方法。
递推公式:
第i阶楼梯可以由i-1阶楼梯跳一步上来,也可以由i-2阶楼梯跳两步上来。
所以到达第i阶楼梯可以有dp[i-1]+dp[i-2]种方法,即dp[i] = dp[i-1]+dp[i-2]。
初始化:
爬上第一阶楼梯有一种方法,即从第0阶向上爬一步,所以dp[1]=1;
爬上第二阶楼梯有两种方法,从第0阶向上一次性爬两步到第二阶,或者向上爬两次,一次爬一步到第二阶,所以dp[2]=2。
遍历顺序:
从前往后依次遍历并确定到达每阶楼梯所需要的方法。
如果结果有问题,打印dp数组,查看是否跟自己推导的一致。
代码如下:
class Solution {public int climbStairs(int n) {if(n <= 2) return n;int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;for(int i = 3; i <= n; i++) dp[i] = dp[i - 1] + dp[i - 2];return dp[n];}
}时间复杂度o(n),空间复杂度o(n).
三、LeetCode746. 使用最小花费爬楼梯
题目链接:746. 使用最小花费爬楼梯
题目描述:
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20] 输出:15 解释:你将从下标为 1 的台阶开始。 - 支付 15 ,向上爬两个台阶,到达楼梯顶部。 总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1] 输出:6 解释:你将从下标为 0 的台阶开始。 - 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。 - 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。 - 支付 1 ,向上爬一个台阶,到达楼梯顶部。 总花费为 6 。
提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
算法分析:
确定dp数组及下标含义:
dp[i]表示到达第i阶楼梯所需花费的最小费用。
递推公式:
到第i阶可以从i-1阶跳一步上来,所需花费为dp[i-1]+cost[i-1],也可以从i-2阶跳两步上来,所需花费为dp[i-2]+cost[i-2],所以到达第i阶所需要的最小花费为dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])。
初始化:
题目给出的条件,我们可以从第0阶或第1阶楼梯开始爬楼梯。
所以爬上第0阶楼梯所需的最小花费dp[0]=0,爬上第1阶所需的最小花费dp[1]=0;
遍历顺序:
从前往后依次遍历并确定到达每阶楼梯所需的最小花费。
如果有问题打印dp数组验证。
代码如下:
class Solution {public int minCostClimbingStairs(int[] cost) {int len = cost.length;int[] dp = new int[len + 1];dp[0] = 0;dp[1] = 0;for(int i = 2; i <= len; i++)dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);return dp[len];}
}时间复杂度o(n),空间复杂度o(n).
总结
解决了这三道题,动态规划算是入门了,这三道题只要按照动规五部曲来还是比较简单的。
动规五部曲:
1,确定dp数组及下标的含义。
2,确定递归公式。
3,初始化。
4,确定遍历顺序。
5,打印dp数组验证结果。
相关文章:
|LeetCode509. 斐波那契数、LeetCode70. 爬楼梯、LeetCode746. 使用最小花费爬楼梯)
LeetCode算法题解(动态规划)|LeetCode509. 斐波那契数、LeetCode70. 爬楼梯、LeetCode746. 使用最小花费爬楼梯
一、LeetCode509. 斐波那契数 题目链接:509. 斐波那契数 题目描述: 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:…...
)
【图像处理】:Otsu算法最大类间方差法(大津算法:附源码)
这里写自定义目录标题 数学原理算法评价参考链接 数学原理 以灰度图像为例,对于图像MN大小的矩阵,即图像中的像素,每一个值即为像素值,其中灰度图像像素值在(0~255)之间。 主要实现前景(即目标)和背景的分割: 主要公式…...

【uni-app】设置背景颜色相关
1. 全局页面背景色设置: 在App.vue的style样式表中设置 <style> page {background-color: #F0AD4E; } </style> 2. 顶部导航栏背景色设置: 在pages.json页面路由中,globalStyle设置 "globalStyle": {"navi…...

工厂模式-C++实现
工厂模式是一个创建型设计模式,即“对象创建模式”,通过这种模式可以绕开new,来避免对象创建过程中,也就是new的方法造成的紧耦合,从而支持对象创建的稳定。 工厂模式中引入了一个工厂类,该工厂负责根据客…...
安装应用与免安装应用差异对比
差异 安装的程序和免安装的应用程序之间有以下几个方面的差别: 安装过程:安装的程序需要通过一个安装程序或安装脚本进行安装。这个过程通常会将应用程序的文件和依赖项复制到指定的目录,并进行一些配置和注册操作。免安装的应用程序则不需要…...

FiscoBcos使用Go调用合约
环境: fisco2.8.0 go 1.17 go-sdk 1.0.0 solidity 0.4.25 前言 请提前启动好四个fisco节点。 请准备好一个属于此fisco节点的账户私钥【待会调用合约和部署合约会用到】 此文章将讲解 官方文档使用gosdk部署helloworld合约并调用其方法 合约开发样例 官网提示 G…...
自然语言处理(NLP)-spacy简介以及安装指南(语言库zh_core_web_sm)
spacy 简介 spacy 是 Python 自然语言处理软件包,可以对自然语言文本做词性分析、命名实体识别、依赖关系刻画,以及词嵌入向量的计算和可视化等。 1.安装 spacy 使用 “pip install spacy" 报错, 或者安装完 spacy,无法正…...

CTF-PWN-tips
文章目录 overflowscanfgetreadstrcpystrcat Find string in gdbgdbgdb peda Binary ServiceFind specific function offset in libc手工自动 Find /bin/sh or sh in library手动自动 Leak stack addressFork problem in gdbSecret of a mysterious section - .tlsPredictable …...

《Effective C++》条款21
必须返回对象时,别妄想返回其reference 如果你的运算符重载函数写成了返回reference的形式: class A { public:A(int a,int b):x(a),y(b){}friend const A& operator*(const A& a, const A& b); private:int x;int y; }; const A& opera…...

决策树,sql考题,30个经典sql题目
大数据: 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle,尤其sql要学&#x…...
)
【ES6.0】- 扩展运算符(...)
【ES6.0】- 扩展运算符... 文章目录 【ES6.0】- 扩展运算符...一、概述二、拷贝数组对象三、合并操作四、参数传递五、数组去重六、字符串转字符数组七、NodeList转数组八、解构变量九、打印日志十、总结 一、概述 **扩展运算符(...)**允许一个表达式在期望多个参数࿰…...

关于Java中的深拷贝与浅拷贝
Java中的深拷贝和浅拷贝是针对对象和数组等引用数据类型的复制操作。 浅拷贝(Shallow Copy): 对于基本数据类型,浅拷贝直接复制其值。对于引用数据类型,浅拷贝只复制对原对象的引用,而不是复制对象本身。因…...

13.真刀实枪做项目---博客系统(页面设计)
文章目录 1.预期效果1.1博客列表页效果1.2博客详情页效果1.3博客登陆页效果1.4博客编辑页效果 2.实现博客列表页2.1实现导航栏2.2实现版心2.3实现个人信息2.4实现博客列表2.5博客列表页完整代码 3.实现博客正文页3.1引入导航栏3.2引入版心3.3引入个人信息3.4实现博客正文3.5博客…...

VScode 配置用户片段
文件->首选项->配置用户片段->新建全局用户片段 后续就可以通过vv3来直接生成下面的代码 {// Place your 全局 snippets here. Each snippet is defined under a snippet name and has a scope, prefix, body and // description. Add comma separated ids of the l…...
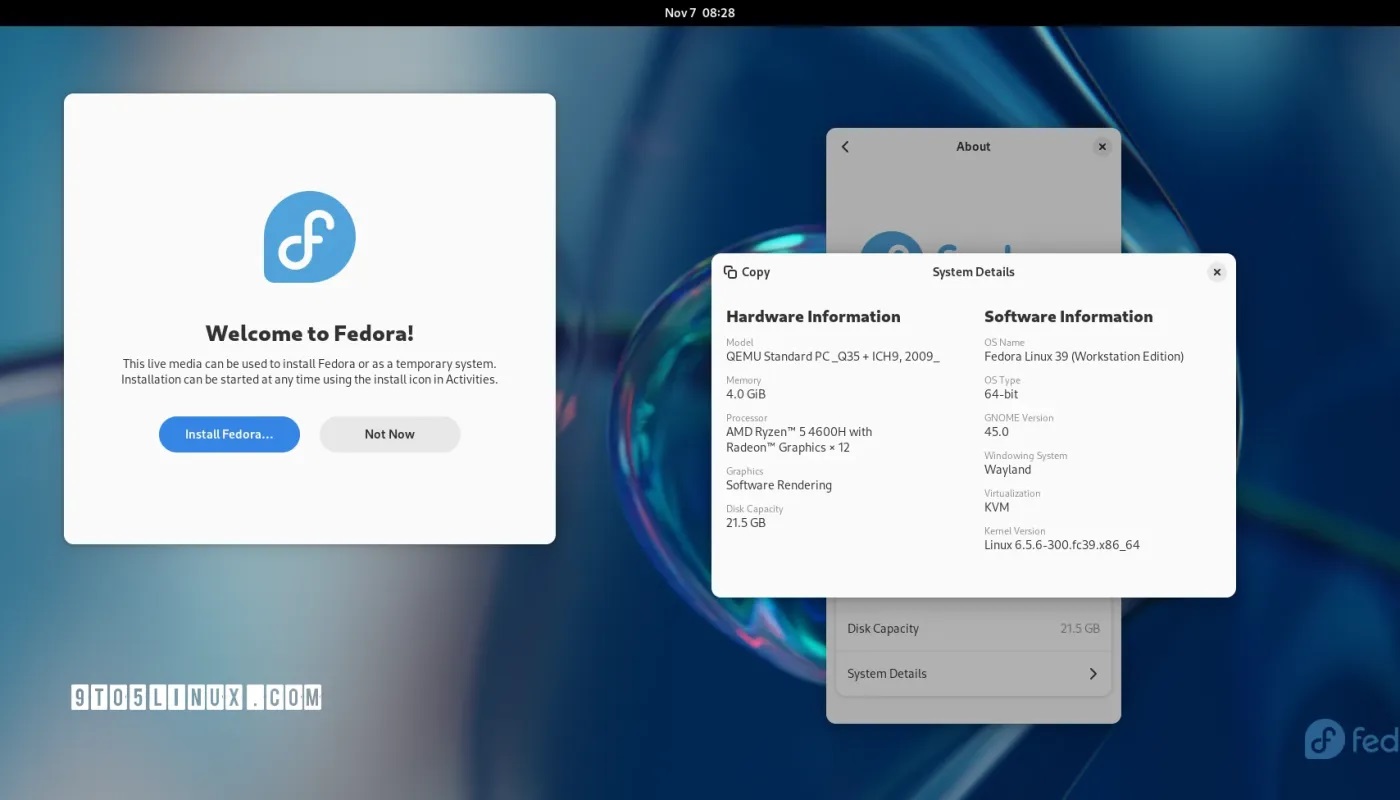
Fedora 项目近日发布了 Fedora Linux 39
导读几经推迟之后,Fedora 项目近日发布了 Fedora Linux 39,这是红帽公司赞助的面向大众的 GNU/Linux 发行版的最新稳定版本,采用了最新的技术和开源应用程序。 Fedora Linux 39 由 Linux 内核 6.5 支持,并提供了一些最新的桌面环境…...

Uniapp连接iBeacon设备——实现无线定位与互动体验(理论篇)
目录 前言: 一、什么是iBeacon技术 二、Uniapp连接iBeacon设备的准备工作 硬件设备: 三、Uniapp连接iBeacon设备的实现步骤 创建Uniapp项目: 四、Uniapp连接iBeacon设备的应用场景 室内导航: 五、Uniapp连接iBeacon设备的未来…...

GCD:异步同步?串行并发?一文轻松拿捏!
GCD 文章目录 GCD进程线程进程与线程的关系进程与线程的区别 任务(执行的代码)队列线程与队列的关系 队列任务**同步执行任务(sync)**辅助方法**异步执行任务(async)**总结栅栏任务迭代任务 队列详细属性QoSAttributes…...

学习c#的第十七天
目录 C# 异常处理 异常的原因 System.Exception 类 如何处理异常 常见的异常类 throw 语句 throw 表达式 try 语句 try-catch 语句 try-finally 语句 try-catch-finally 语句 when 异常筛选器 异步和迭代器方法中的异常 C# 异常处理 C # 中的异常提供了结构化、统…...

龙芯 操作系统选择和安装
龙芯3a5000及之后的cpu底层架构已经从mips64el改为了loongarch64 所以这里分了2种来说明,分别对应3a4000之前的和3a5000之后的 龙芯的系统安装难点在于操作系统的选取和引导 一、烧录工具 制作安装盘使用常规的烧录工具是不行滴,会提示没有\boot\initrd…...
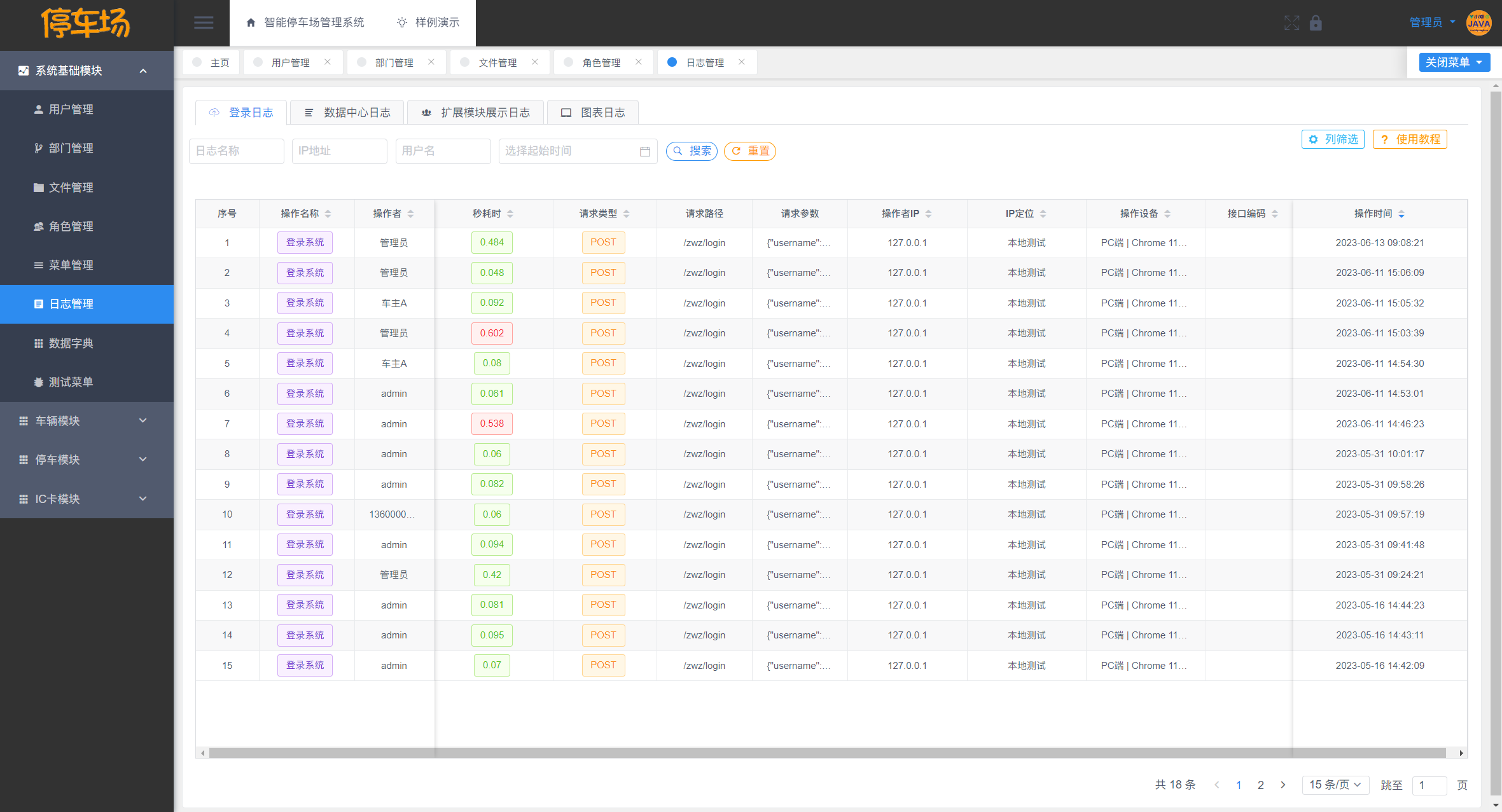
【开源】基于JAVA的智能停车场管理系统
项目编号: S 005 ,文末获取源码。 \color{red}{项目编号:S005,文末获取源码。} 项目编号:S005,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容A. 车主端功能B. 停车工作人员功能C. 系…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
