leetcode 427. Construct Quad Tree(构建四叉树)

刚看到题的时候是懵的,这也太长了。到底是要表达什么呢。
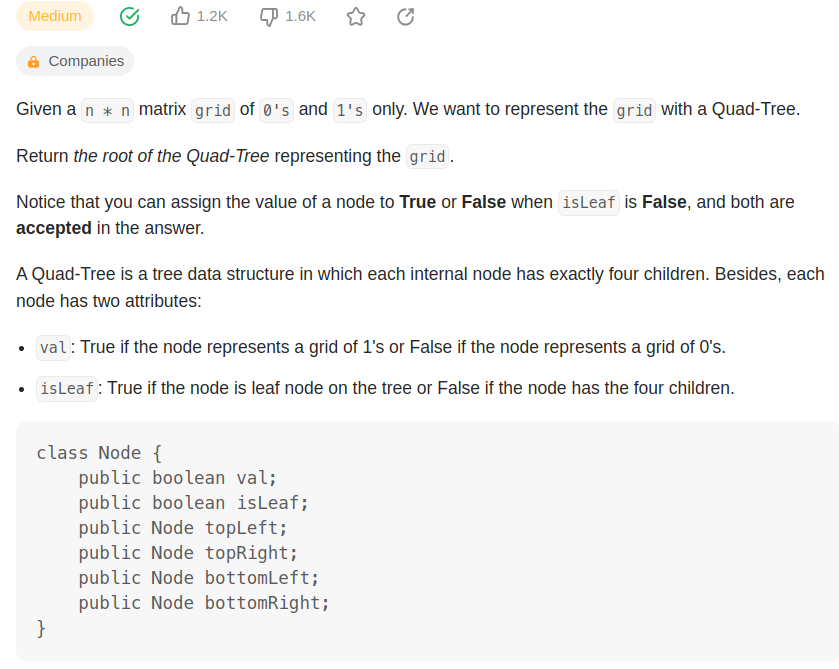
不妨把这个矩阵看成一个正方形的图片,想象你在处理图片,从整体逐步到局部。
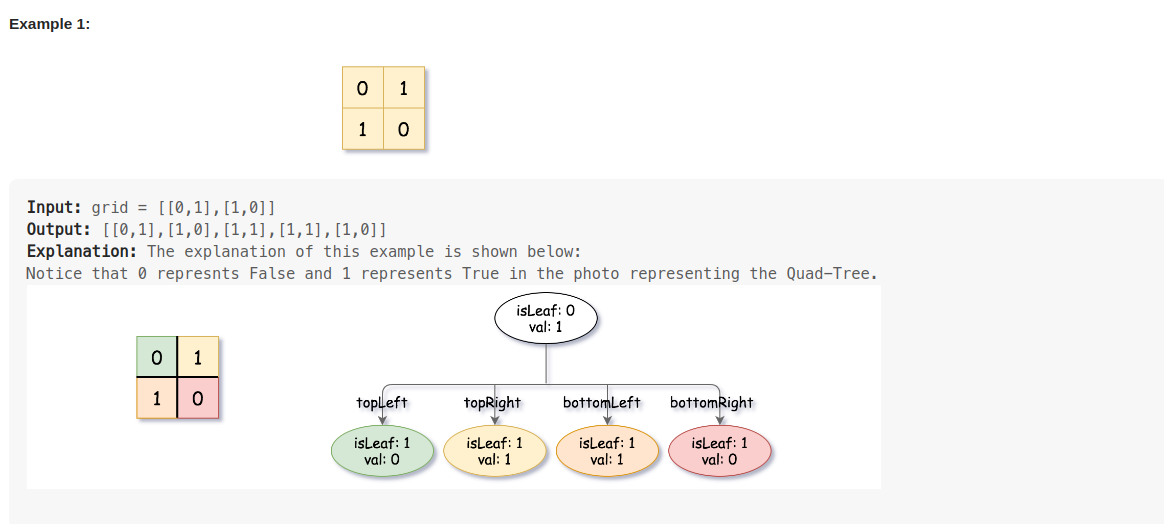
刚开始看一整张图片,如果是全0或全1,这个就是叶子节点,怎么表达叶子节点呢,就是isLeaf=true, val=0 or 1(全0 or 全1),
这个isLeaf和val会组成一个Node.
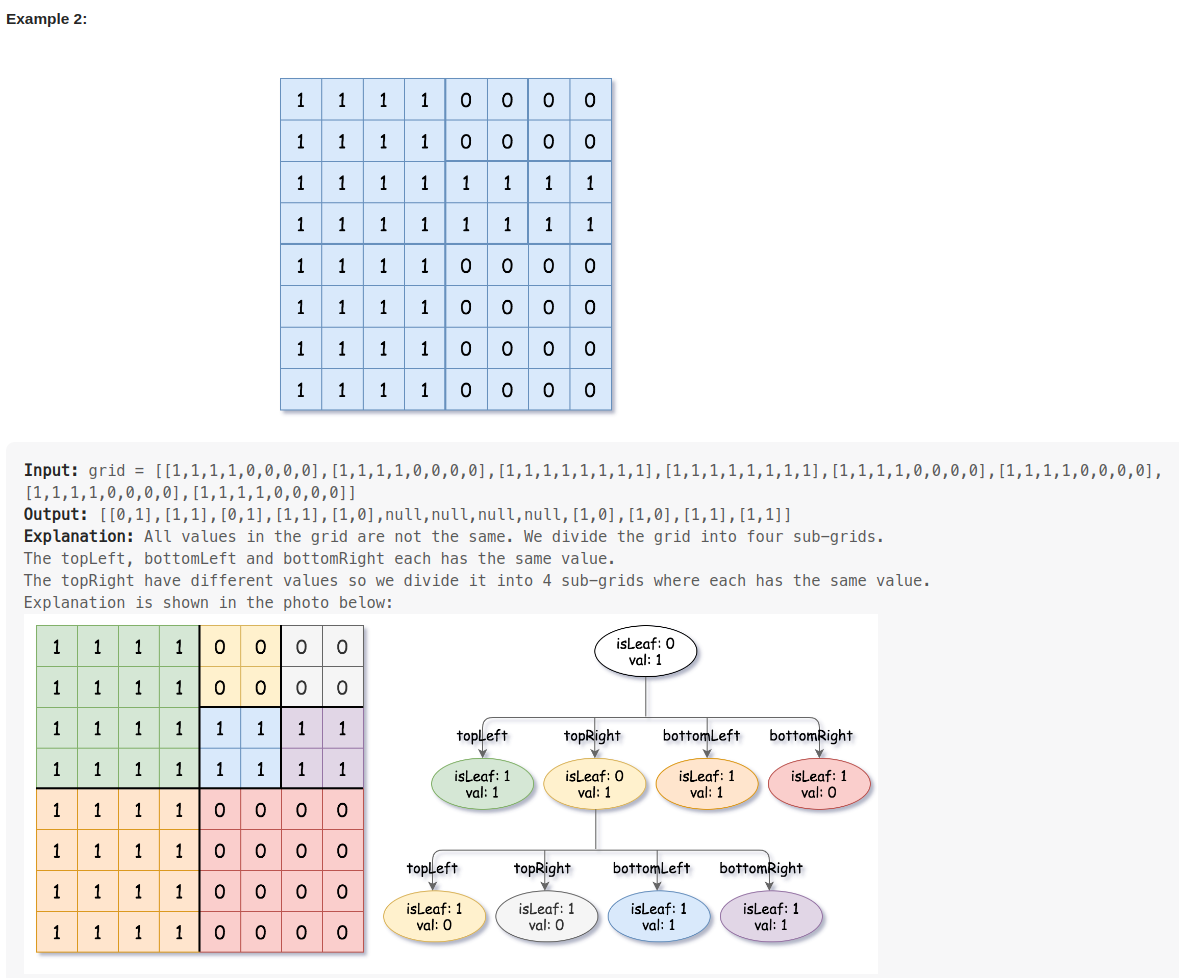
如果不是全0或全1,那就不是叶子节点,就要把图片等分成4块,左上的一块叫topLeft, 右上的一块叫topRight,
同理bottomLeft, bottomRight,
这4块按同样的方法再进入下一轮:
全0或全1就是叶子节点,否则再细分成4小块,再处理。
不是叶子节点时,isLeaf=false, val=0 or 1都行,这里统一为1.
最后返回四叉树的根。
思路:
分而治之。
简单看下流程吧:
首先一整个矩阵,判断是否全0或全1,
是:叶子节点(isLeaf = true, val=0 or 1), 返回这个节点。
否:建立当前节点作为root(isLeaf = false, val = 1),
然后把矩阵等分成4小块,分别把左上,右上,左下,右下四小块返回的结果给root.topLeft, root.topRight …
每个小块的处理过程重复上面的步骤。
至于怎么分成小块,已知每个小块的左上角坐标(r,c)和边长,又知grid, 就可取出对应的小块。
树的节点建立有点类似于树的前序遍历。
class Solution {public Node construct(int[][] grid) {int n = grid.length;return buildNode(grid, 0, 0, n);}Node buildNode(int[][] grid, int r, int c, int len) {if(allSame(grid, r, c, len))return new Node(grid[r][c] == 1 ? true : false, true);Node root = new Node(true, false);root.topLeft = buildNode(grid, r, c, len/2); //矩阵起点的(r,c)和边长root.topRight = buildNode(grid, r, c+len/2, len/2);root.bottomLeft = buildNode(grid, r+len/2, c, len/2);root.bottomRight = buildNode(grid, r+len/2, c+len/2, len/2);return root;}boolean allSame(int[][] grid, int r, int c, int len) {int cur = grid[r][c];for(int i = r; i < r + len; i++) {int[] cols = grid[i]; //一维数组比二维数组高效for(int j = c; j < c + len; j++) {if(cols[j] != cur) return false;}}return true;}
}
相关文章:

leetcode 427. Construct Quad Tree(构建四叉树)
刚看到题的时候是懵的,这也太长了。到底是要表达什么呢。 不妨把这个矩阵看成一个正方形的图片,想象你在处理图片,从整体逐步到局部。 刚开始看一整张图片,如果是全0或全1,这个就是叶子节点,怎么表达叶子节…...
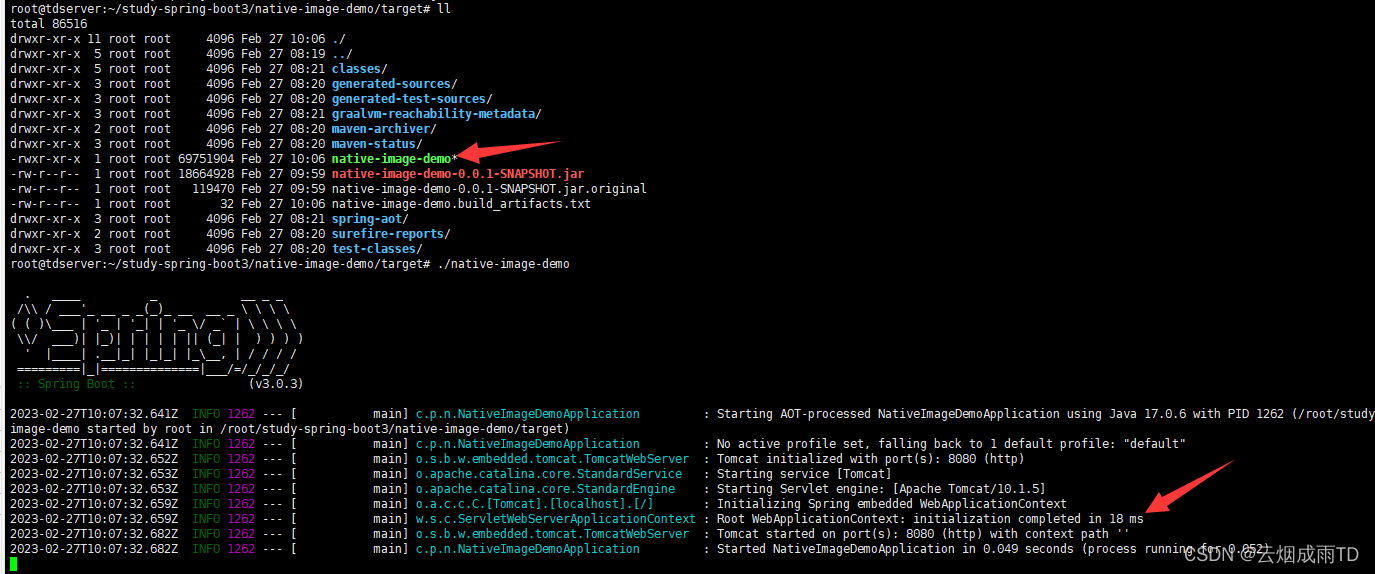
Spring Boot 3.0系列【2】部署篇之使用GraalVM构建原生镜像
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot版本2.7.0 文章目录概述JIT & AOTJIT (动态编译)AOT(静态编译)GraalVM简介运行模式Native Image(原生镜像)…...
复习知识点十之方法的重载
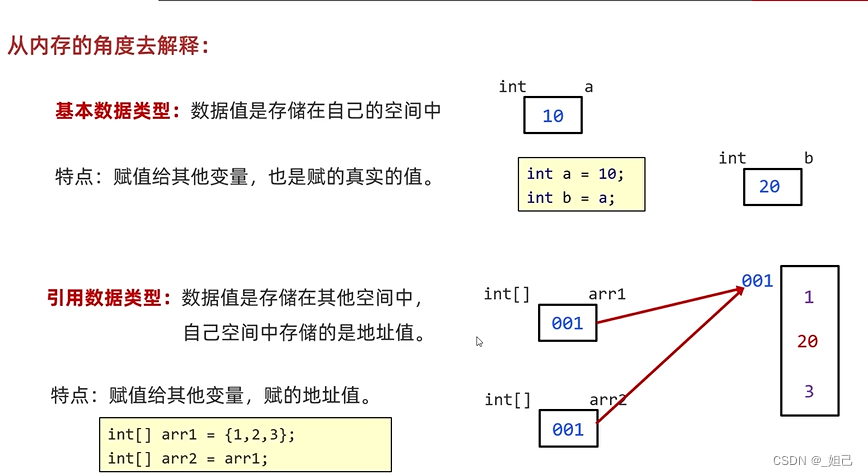
目录 方法的重载 练习1: 练习1: 数组遍历 练习2: 数组的最大值 练习3: 练习4: 复制数组 基本数据类型和引用数据类型 方法的重载 Java虚拟机会通过参数的不同来区分同名的方法 练习1: public class Test4 {public static void main(String[] args) {//调用方法 // …...

火爆全网的ChatGPT 和AI 可以为项目经理做什么?
作为一款人工智能聊天机器人,ChatGPT因其逼真和人性化的特性而风靡全球,无疑是当今技术的新流行。人工智能 (AI) 有可能彻底改变许多行业,包括项目管理,及时了解最新技术以及它如何影响你的工作至关重要。于是,我们与C…...

前端面试题 —— HTML
目录 一、src 和 href 的区别 二、对 HTML 语义化的理解 三、DOCTYPE(⽂档类型) 的作⽤ 四、script 标签中 defer 和 async 的区别 五、常⽤的 meta 标签有哪些? 六、HTML5 有哪些更新 八、行内元素有哪些?块级元素有哪些? 空(void)元素…...

同为(TOWE)电源线让家用电器随心放置
如今,随着科技水平的不断发展,人们工作、生活中越来越离不开各类电子设备和电器产品。当用电器数量多了以后,由于电器设备原有电线长度的限制,常常需要通过连接接线板来延长电器设备的电能传输线路。电源线虽然看着是一件不起眼的…...
)
2023上半年数学建模竞赛汇总(报名时间、比赛时间、难易程度、含金量、竞赛官网)
1、美国大学生数学建模竞赛等级:国家级是否可跨校:否竞赛开始时间:2月17日~2月21日综合难度:⭐⭐⭐⭐ 竞赛含金量:⭐⭐⭐⭐⭐竞赛官网:https://www.comap.com/2、MathorCup高校数学建模挑战赛---大数据竞赛…...

RK3568平台开发系列讲解(驱动基础篇)SMP(Symmetrical Multi-Processing)
🚀返回专栏总目录 文章目录 一、linux SMP 和 AMP二、linux SMP的启动流程三、CPU的描述:cpumask四、CPU之间的关系沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇将介绍 SMP(Symmetrical Multi-Processing)。 一、linux SMP 和 AMP 目前支持多核处理器的实时操…...

HIVE --- zeppelin安装
目录 把zeppelin压缩包拷贝到虚拟机里面 解压 改名 修改配置文件 编辑zeppelin-site.xml—将配置文件的ip地址和端口号进行修改 编辑 zeppelin-env.sh—添加JDK和Hadoop环境 配置环境变量 刷新环境变量 拷贝Hive文件 拷贝外部文件 启动zeppelin 启动Hadoop&Hi…...

数据分析中的变量解释
1.数值变量Numerical Variables 数值型变量(metric variable)是说明事物数字特征的一个名称,其取值是数值型数据。如“产品产量”、“商品销售额”、“零件尺寸”、“年龄”、“时间”等都是数值型变量,这些变量可以取不同的数值…...

django-博客(一)
一、 1、环境:pycharm,python3.6,django3,mysql8.0 2、创建项目 3、把html和css样式那些导入到文件夹中,然后配置这些文件夹的路径,再添加首页视图。 改成反向解析 python manage.py runserv…...
Shell高级——Linux中的文件描述符
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 前言 Linux中一切接文件,比如 C 源文件、视频文件、Shell脚本、可执行文件等,就连键盘、显示器、鼠标等硬件设备也都是文件。 一个 Linux 进程可以打开成百上…...

洗地机哪个品牌最好用?家用洗地机十大名牌
这几年清洁类的小家电非常热门,无线吸尘器、扫地机器人、扫拖一体机、洗地机和擦窗机器人层出不穷,各个品牌百花齐放。这些清洁电器,确实为家庭卫生清洁带来了很大的便捷。但要把这些产品一次性买齐是一笔不小的开销,而且需要收纳…...
线程休眠)
java多线程(十)线程休眠
一、sleep()介绍 sleep() 定义在Thread.java中。 sleep() 的作用是让当前线程休眠,即当前线程会从“运行状态”进入到“休眠(阻塞)状态”。sleep()会指定休眠时间,线程休眠的时间会大于/等于该休眠时间;在线程重新被唤醒时,它会由…...

Leetcode20. 有效的括号
一、题目描述: 给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确…...
Android 项目必备(四十三)-->Android 开发者的 new 电脑
前言 作为 Android 开发者,当你新入职一家公司,拿到新发的电脑,你会对电脑干点啥? 安装开发环境?装软件?你是否还会铺天盖地到处找之前电脑备份的东西?又或者还想不起来有什么上一台电脑好用的…...

如何水平和垂直居中元素
跳到主内容 我试图将我的选项卡内容垂直居中,但是当我添加 CSS 样式时display:inline-flex,水平文本对齐消失了。 如何为每个选项卡同时对齐文本 x 和 y? * { box-sizing: border-box; } #leftFrame {background-color: green;position: a…...

Rust泛型Generics
泛型 泛型(Generics)是一种程序设计风格,它允许程序员在强类型语言(例如rust,c#,c)中编写代码时使用通用类型。以rust为例,如果你想实现一个通用的add函数,让其在u8, i3…...
六、并发集合
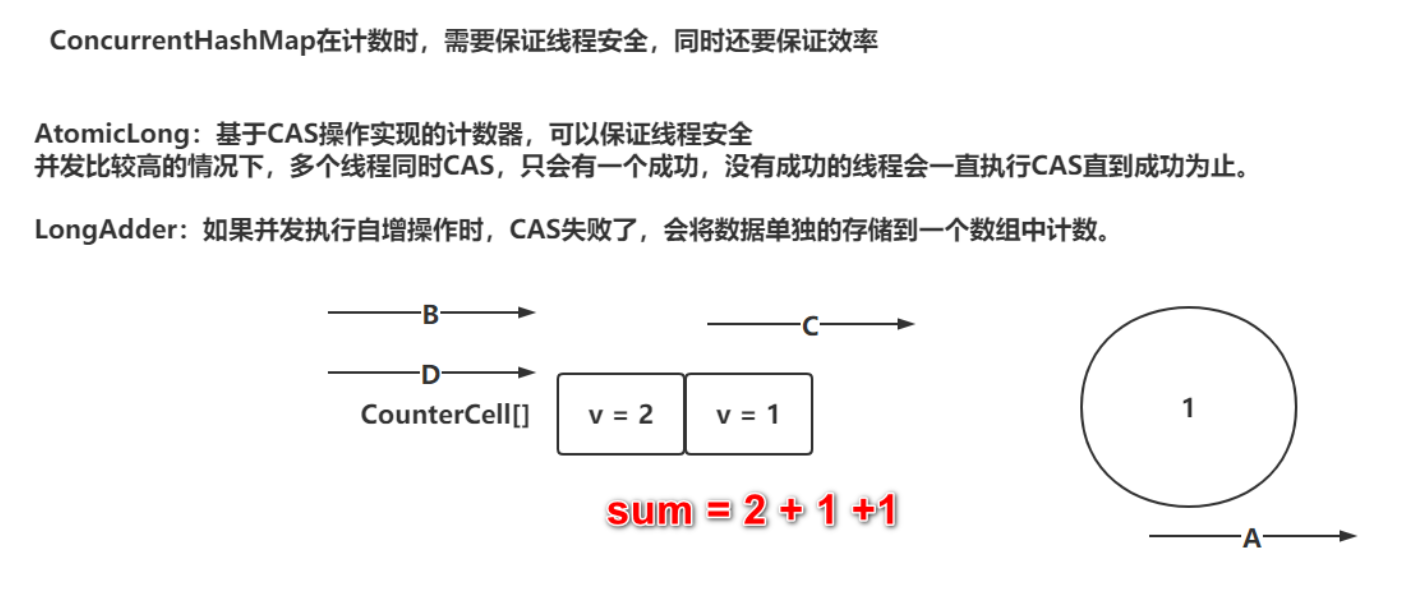
文章目录并发集合ConcurrentHashMap存储结构存储操作put方法putVal方法-散列算法putVal方法-添加数据到数组&初始化数组putVal方法-添加数据到链表扩容操作treeifyBin方法触发扩容tryPreSize方法-针对putAll的初始化操作tryPreSize方法-计算扩容戳并且查看BUGtryPreSize方法…...

PHY调试经验
1. PHY调试过程 1.设备树中配置正确的PHY ADDR、PHY ID、clause 45或者22协议,PHY ADDR配置不正确会导致MDC/MDIO通信不正常或失败,PHY ID用于匹配PHY驱动程序。 2.通过MDC/MDIO读写PHY ID并对比datasheet中的PHY ID,确认MDC/MDIO通信是否正常…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
