C语言第入门——第十六课
目录
一、分治策略与递归
二、递归
1.求解n的阶乘
2.输入整数、倒序输出
3.输入整数、正序输出
4.计算第n位Fibonacci数列
编辑5.无序整数数组打印
6.找到对应数组下标
一、分治策略与递归
在我们遇到大问题的时候,我们的正确做法是将它分解成小问题,然后一个小问题一个小问题解决,这样的策略就是分治策略。
递归是分治策略的一种方式,可以不断地通过自己调用自己来将问题规模逐渐缩小,从而解决问题。
分治策略的特征:
①大规模问题化成小规模问题容易被解决掉
②大规模问题能够被划分为多个相同的小规模问题
③这些小规模问题的解组合起来是大问题的解
④小规模问题是相互独立的
举个例子:
皇帝让你数10个谷仓的米粒,问题规模太大,你可以找100个工人,每人分上相同重量的米进行数,每个人的数量相加就是最终米粒的数量。
这就是一个典型的分治策略问题,将大规模转化为小规模问题,而且是满足上面分治策略的四条特征的。
分治策略不光在我们算法中需要使用,我希望转化成我们的思维模式,帮助我们更好的解决生活中的问题。
二、递归
递归包含两个过程:递推和回归,递推逐层调用,直到递推终止条件满足,再逐层回归。
递归和普通函数调用类似,需要开辟栈帧空间,它只有满足中止条件逐层回归的时候,上一层的函数的栈帧空间才会被释放。注意,不存在无限递归的函数,因为栈帧空间是有限的,所以不能无限调用函数,开辟空间。
递归分为直接递归和间接递归。
直接递归:在函数执行的时候调用函数自身。
间接递归:在函数执行过程中调用其他函数,再调用函数自身。
一般不推荐使用间接递归,因为很容易递推错误。
1.求解n的阶乘
代码如下:
int fabi(int n)
{if (n == 1) return 1;int sum = fabi(n-1)*n;return sum;
}int main()
{int n = 0;scanf("%d", &n);int sum =fabi(n);printf("%d", sum);
}
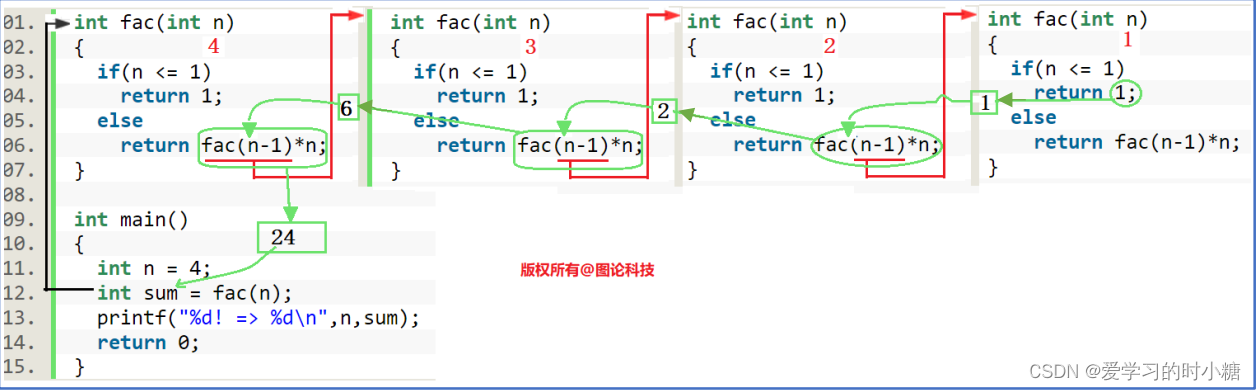
分析:我们将代码复制多份便于观看,但其实只有一个代码哦。
我们这里取n=4,第一次进入到fabi()函数中,n!=1,执行下一条语句fabi(n-1)*n,也就是fabi(3)*4。
然后我们再次调用函数fabi(),此时n=3,我们进入到函数体中n!=1,执行下一条语句fabi(2)*3。
此时我们再次调用fabi()函数,此时n=2,n!=1,执行fabi(1)*2。
这里再次调用fabi()函数,此时n==1,所以我们return 1。
返回到上一层,我们继续执行,此时这条语句为sum = 1*2,我们返回1*2,然后我们继续回归上一层函数,sum = 3*2*1,然后我们再回归,最后得到sum =4*3*2*1,回归结束。
下面第一张是我画的示意图,如果看不清楚再看下面第二张老师画的图,老师画的比较清晰。

红色的线代表递推过程,绿色的线代表回归过程。
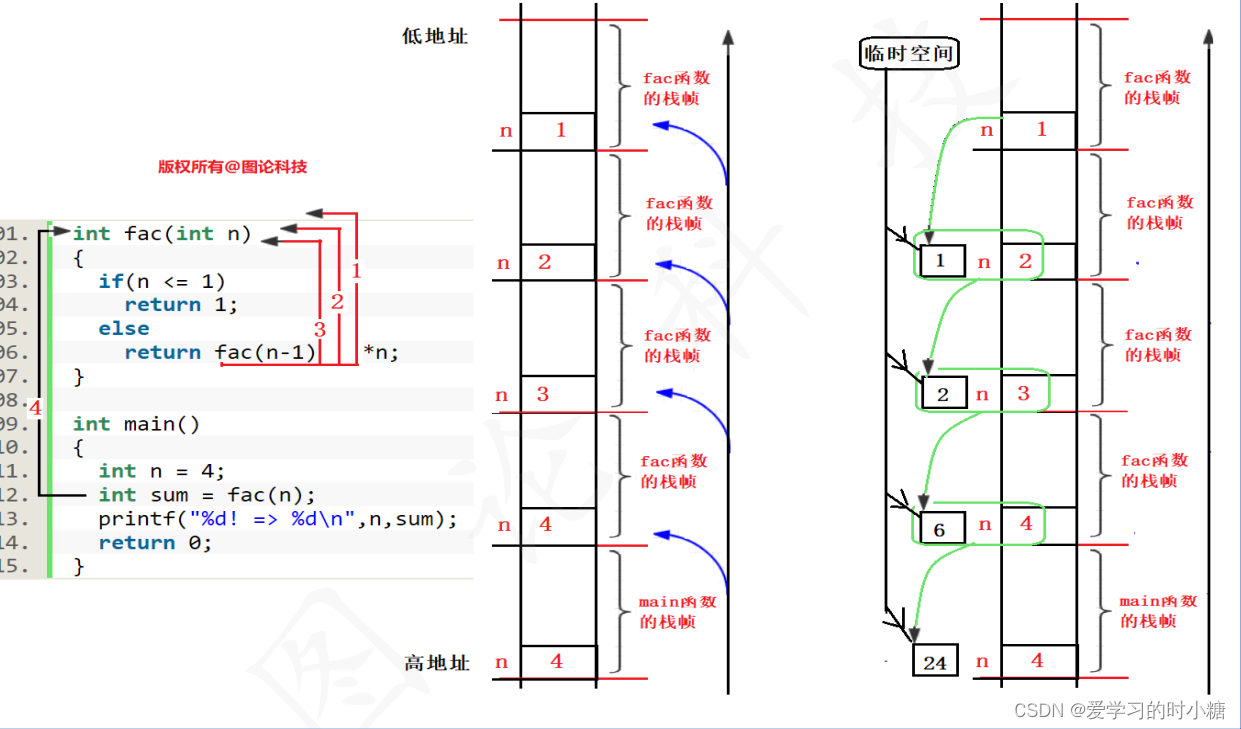
下面解释一下栈帧的动态变化情况。
在每次递推调用函数的时候,程序开辟栈帧空间,在回归的时候再一层层释放掉。
2.输入整数、倒序输出
输入一个整数(无符号整型),使用递归算法将整数倒序输出。
void Show(unsigned int n)
{if (n == 0) return ;else{printf("%d", n % 10);Show(n / 10);}
}
int main()
{unsigned int n = 0;scanf("%d", &n);Show(n);
}
逻辑图如下,变量和函数定义不太一样,但是逻辑一致。
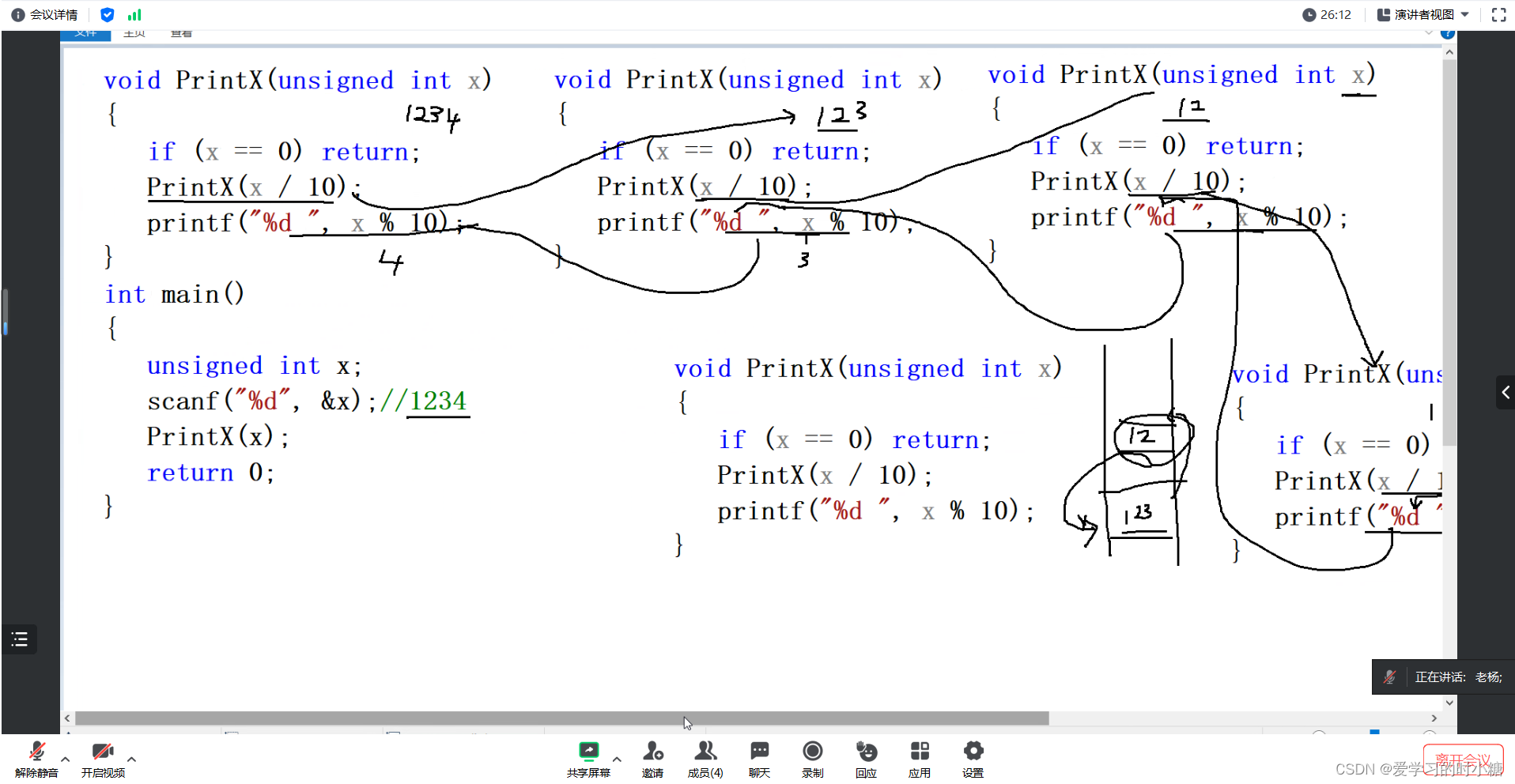
3.输入整数、正序输出
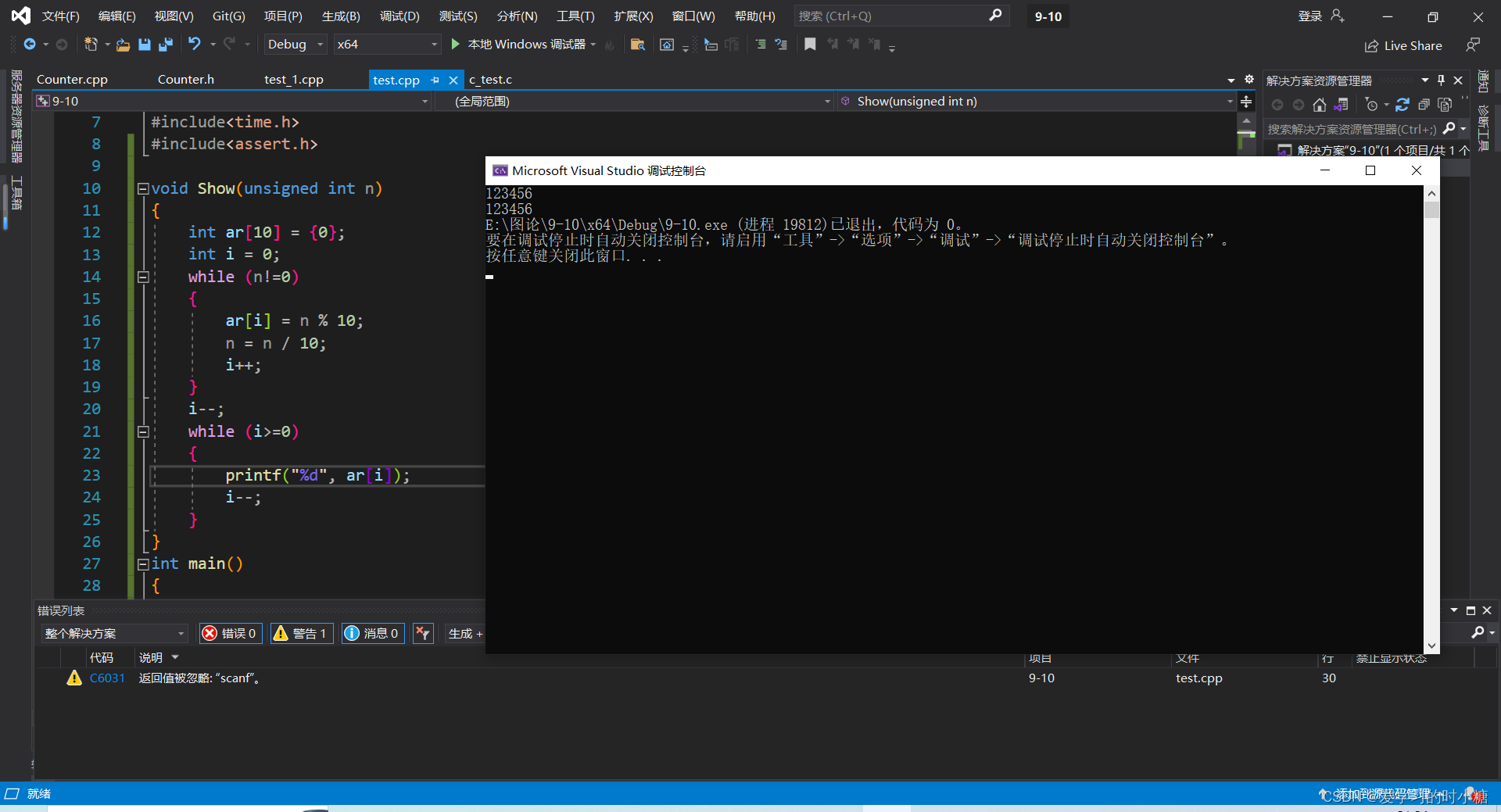
法一:数组法
void Show(unsigned int n)
{ int ar[10] = {0};int i = 0;while (n!=0){ar[i] = n % 10;n = n / 10;i++;}i--;while (i>=0){printf("%d ", ar[i]);i--;}
}
int main()
{unsigned int n = 0;scanf("%d", &n);Show(n);
}
法二:递归法
void Show(unsigned int n)
{if (n == 0) return;else{Show(n / 10);printf("%d", n % 10);}
}
int main()
{unsigned int n = 0;scanf("%d", &n);Show(n);
}
4.计算第n位Fibonacci数列
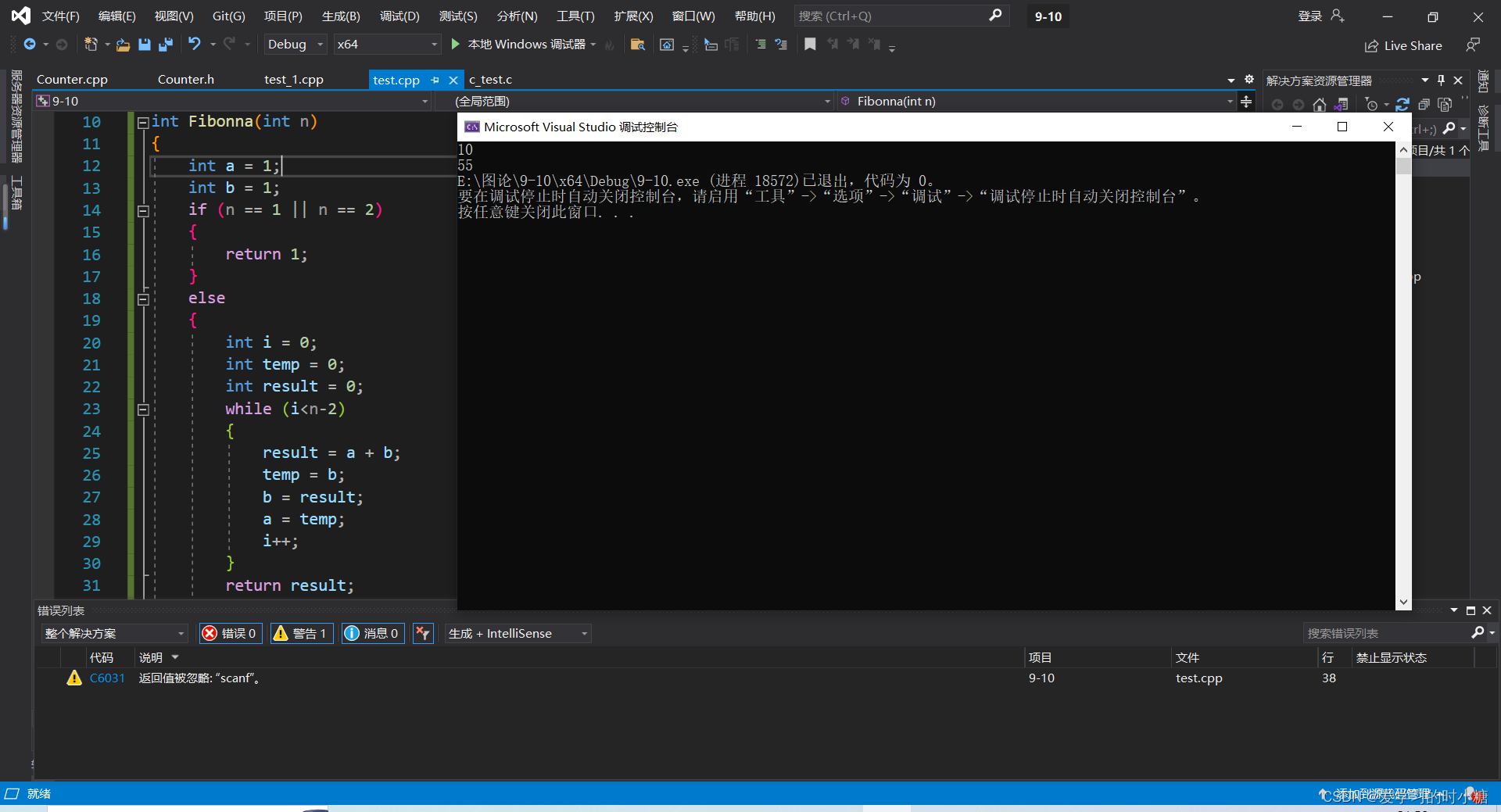
法一:循环输出
int Fibonna(int n)
{int a = 1;int b = 1;if (n==0) return 0;if (n == 1 || n == 2){return 1;}else{int i = 0;int temp = 0;int result = 0;while (i<n-2){result = a + b;temp = b;b = result;a = temp;i++;}return result;}}
int main()
{int n = 0;scanf("%d", &n);int result = Fibonna(n);printf("%d", result);
}
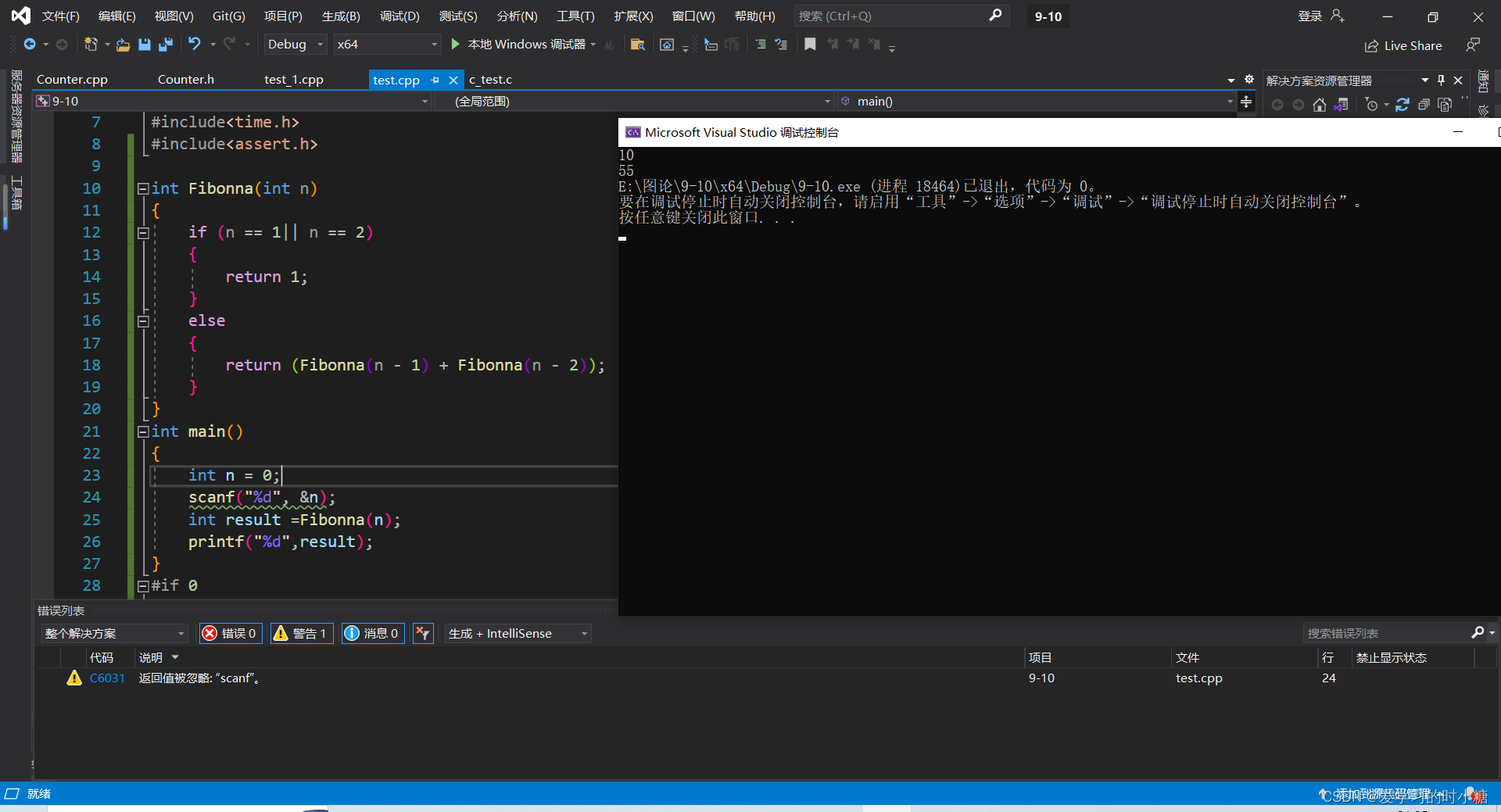
法二:递归输出
int Fibonna(int n)
{if (n == 0) return 0;if (n == 1|| n == 2){return 1;}else{return (Fibonna(n - 1) + Fibonna(n - 2));}
}
int main()
{int n = 0;scanf("%d", &n);int result =Fibonna(n);printf("%d",result);
}
Q: 使用递归进行输出的时候空间复杂度是2^n,很大,怎么样降低时间复杂度?
A: 想要降低复杂度,主要就是要减少一个递归函数,将递归过程中的值存储下来就能减少相应的复杂程度。
写法一:一定要注意a,b,temp不能每次被调用的时候都初始化,要不然输出的值不正确。
int fac(int n)
{static int a = 1;static int b = 1;static int temp = 1;if (n <= 2) return temp;temp = a + b;b = a;a = temp;fac(n - 1);
}
int main()
{int n = 0;scanf("%d", &n);int result = fac(n);printf("%d", result);
}
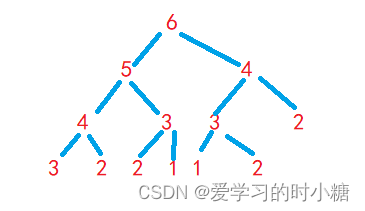
写法二:思路一致,只不过老师写的更清楚明了。
int fanc(int n, int a, int b)
{if (n <= 2) return a;else return fanc(n - 1, a + b, a);
}
int fac(int n)
{int a = 1;int b = 1;return fanc(n, a, b);
}
int main()
{int n = 0;scanf("%d", &n);int result = fac(n);printf("%d", result);
} 5.无序整数数组打印
5.无序整数数组打印
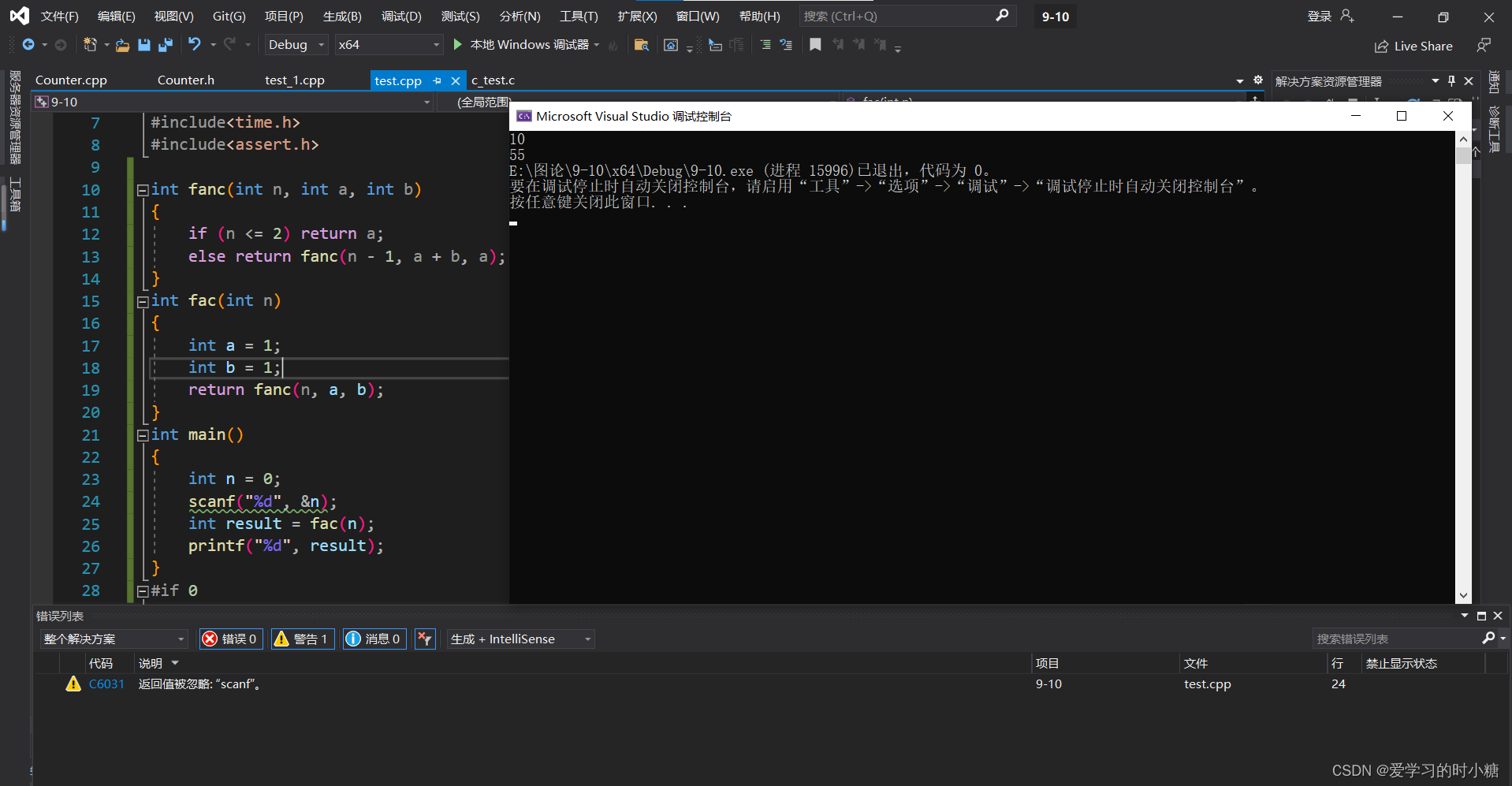
有一个整型数组,数值无序,使用循环和递归打印和查询。
法一:循环打印
void Show_Arr(const int* ar, const int n)
{if (n < 1 || ar == NULL) return;for (int i = 0; i < n; i++){printf("%d ", ar[i]);}
}
int main()
{const int n = 3;int ar[n] = { 12,23,34 };Show_Arr(ar,n);
} 法二:使用递归打印数组
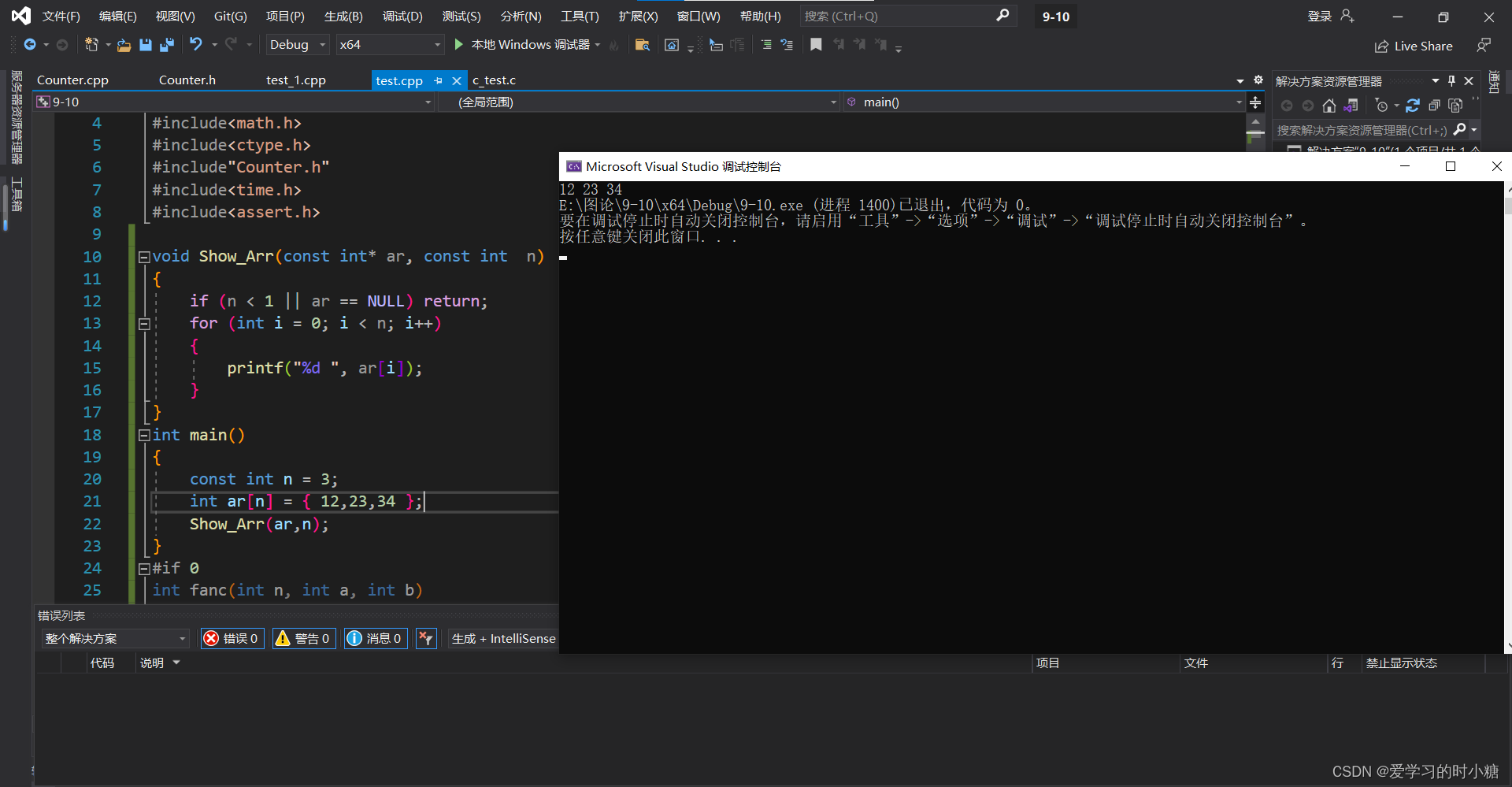
法二:使用递归打印数组
void Show_Arr(const int* ar, const int n)
{if (n < 1 || ar == NULL) return;Show_Arr(ar, n - 1);printf("%d ", ar[n - 1]);}
int main()
{const int n = 3;int ar[n] = { 12,23,34 };Show_Arr(ar, n);
}
Q:上述递归代码我可可以将n-1修改成n--吗?请详细说明。
A:不可以修改,后置--是先取值后--,在下面示例中,n=3,n>0,调用函数,调用的新的函数还是n=3的函数,进入到一个循环,直到栈帧空间被填满。

Q:上述递归代码我可可以将n-1修改成--n吗?请详细说明。
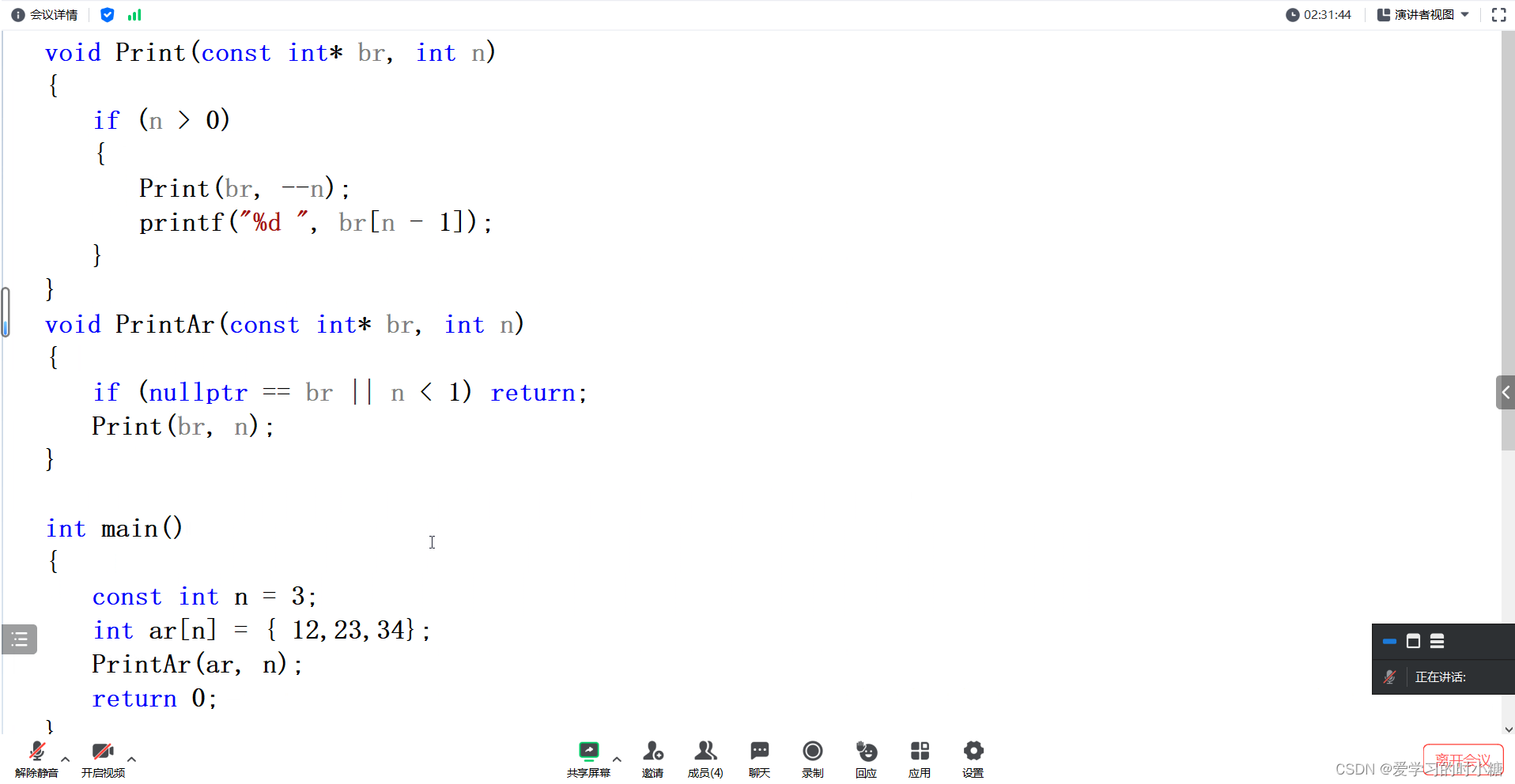
A:也不可以修改,前置--是先--再取值,的确可以满足递归调用的逻辑,但是当他进行回归的时候会n的值被更改了,输出的是更改后的n-1,造成数据溢出问题。

6.找到对应数组下标
法一:循环找数组下标
int FindValue(const int* arr, int n, int value)
{if (n < 1 || arr == NULL) return 0;int pos = -1;for (int i = 0; i < n; i++){if (arr[i] == value){pos = i;break;}}return pos;
}
int main()
{const int n = 5;int arr[n] = { 10,11,12,13,14 };int val = 0;scanf("%d", &val);int m = FindValue(arr, n, val);printf("%d", m);
}
法二:递归找数组下标
这面这个代码输出的数组下标有问题,一直是-1
int FindValue(const int* br, int n, int val)
{int pos = -1;if (NULL == br || n < 1) return pos;if (br[n-1] == val){pos = n - 1;}else{FindValue(br, n - 1, val);}return pos;
}
int main()
{const int n = 5;int arr[n] = { 10,11,12,13,14 };int val = 0;scanf("%d", &val);int m=FindValue(arr,n,val);printf("%d", m);
}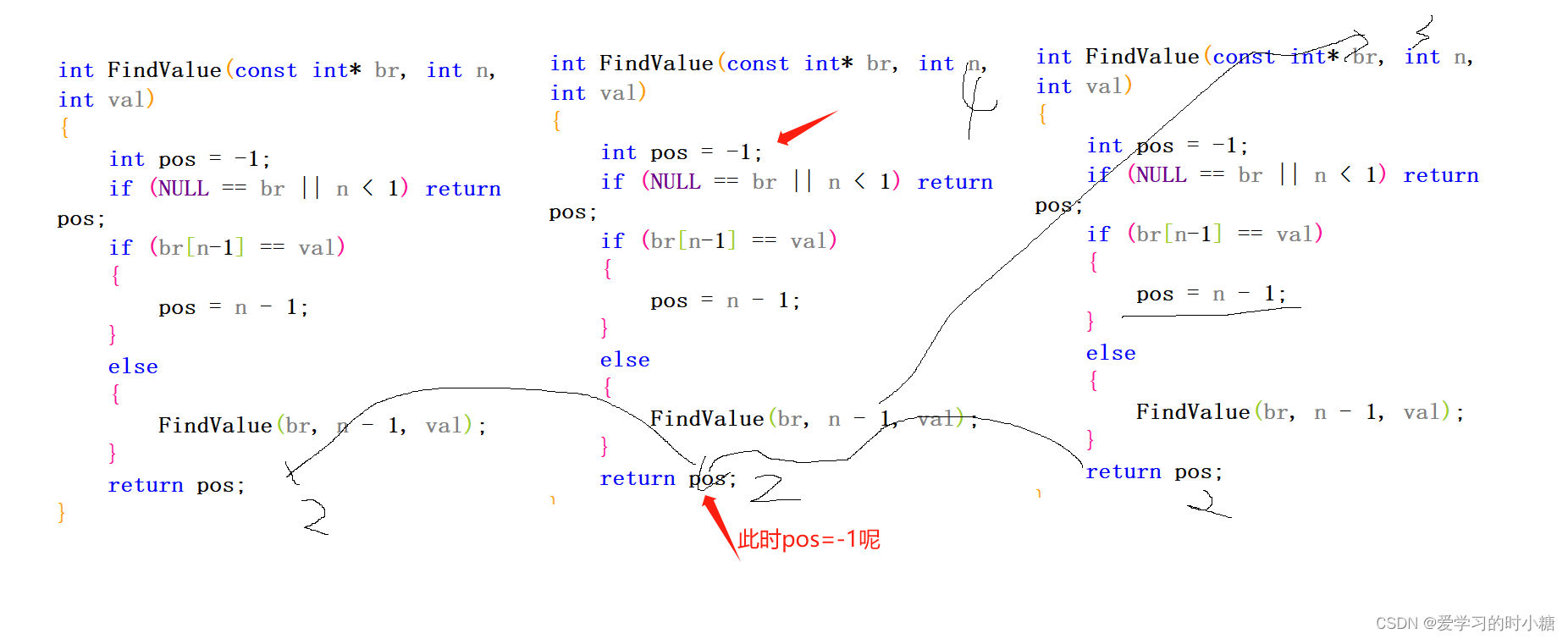
正确代码
int FindValue(const int* br, int n, int val)
{int pos = -1;if (NULL == br || n < 1) return pos;if (br[n-1] == val){pos = n - 1;}else{pos =FindValue(br, n - 1, val);}return pos;
}
int main()
{const int n = 5;int arr[n] = { 10,11,12,13,14 };int val = 0;scanf("%d", &val);int m=FindValue(arr,n,val);printf("%d", m);
}
相关文章:

C语言第入门——第十六课
目录 一、分治策略与递归 二、递归 1.求解n的阶乘 2.输入整数、倒序输出 3.输入整数、正序输出 4.计算第n位Fibonacci数列 编辑5.无序整数数组打印 6.找到对应数组下标 一、分治策略与递归 在我们遇到大问题的时候,我们的正确做法是将它分解成小问题&a…...

IntelliJ IDEA 快捷键 Windows 版本
前言:常用快捷键 IntelliJ IDEA编辑器大受欢迎的原因之一是它的智能提示和丰富的快捷键,在日常开发中熟练的使用快捷键会大大提升开发的效率,本篇文章就笔者日常开发中的总结,把常用的、好用的快捷键做一个列表,方便…...

重生之我必去大厂java开发
JavaDreamer 重生之我必去大厂java开发。主线任务进入大厂java开发。 author :developer_zxh GitHub | Gitee 本项目记录了本人从中国科学院大学硕士研究生开始,如何进入大工 java 开发岗位的学习记录(目前在校未求职,加入后此状…...
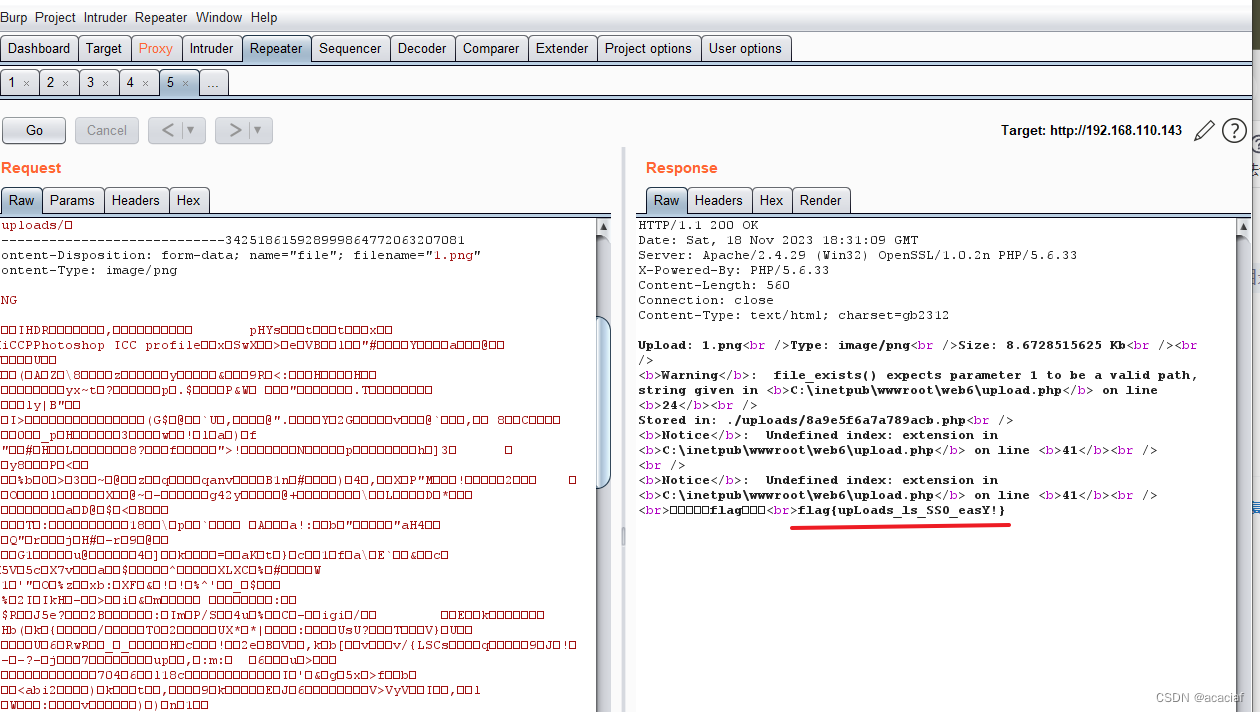
2023年中职“网络安全“—Web 渗透测试②
2023年中职“网络安全“—Web 渗透测试② Web 渗透测试任务环境说明:1.访问http://靶机IP/web1/,获取flag值,Flag格式为flag{xxx};2.访问http://靶机IP/web2/,获取flag值,Flag格式为flag{xxx};3.访问http://靶机IP/web…...
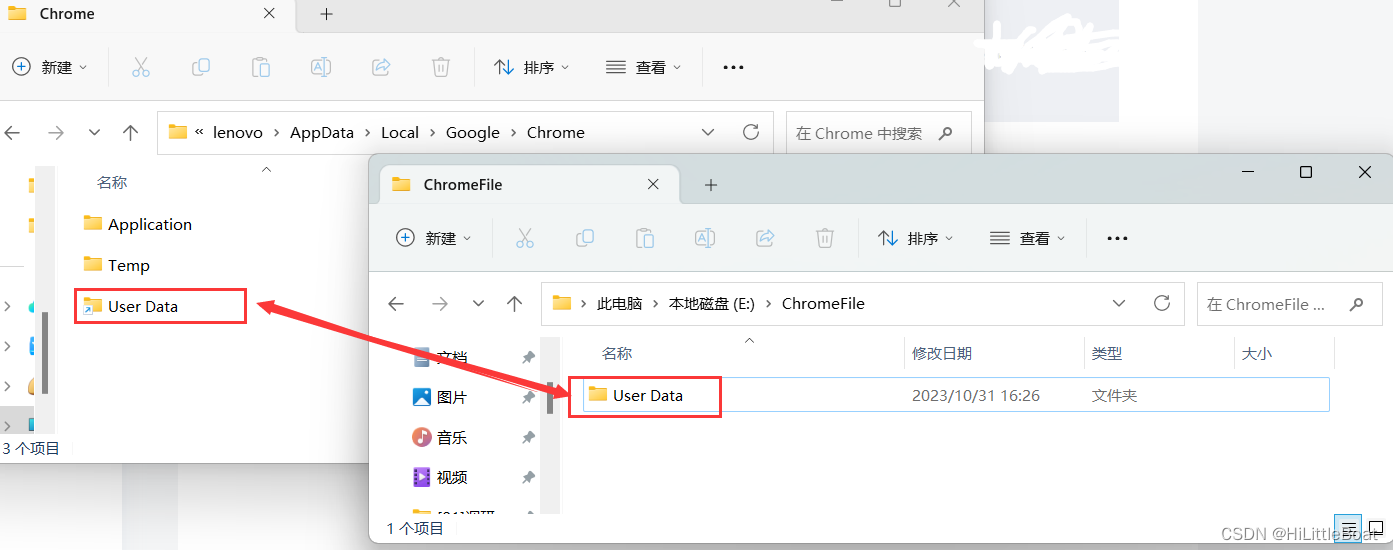
【整顿C盘】pycharm、chrome等软件,缓存移动
C盘爆了,特来找一下巨大的软件缓存,特此记录,跟随的各大教程,和自己的体会 一、爆炸家族JetBrains 这个适用于pycharm、idea、webstorm等等,只要是JetBrains家的,2020版本以上,都是一样的方法 p…...

C# using语句使用介绍
在C#中,using语句有两种主要用途:一是引入命名空间,二是提供一种简便的方式来处理资源的清理(主要用于实现了 IDisposable 接口的对象)。 引入命名空间:using 语句用于引入命名空间,从而可以在代…...
 201. 数字范围按位与 (位运算))
leetcode (力扣) 201. 数字范围按位与 (位运算)
文章目录 题目描述思路分析完整代码 题目描述 给你两个整数 left 和 right ,表示区间 [left, right] ,返回此区间内所有数字 按位与 的结果(包含 left 、right 端点)。 示例 1: 输入:left 5, right 7 输出…...
Flutter笔记: 在Flutter应用中使用SQLite数据库
Flutter笔记 在Flutter应用中使用SQLite数据库(基于sqflite) 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/q…...
OpenAI GPT5计划泄露
OpenAI的首席执行官萨姆奥特曼在最近接受《金融时报》的专访时,分享了OpenAI未来发展的一些新动向。此外,他还透露了关于即将到来的GPT-5模型以及公司对AGI的长期目标的一些细节。 奥特曼指出: 1.OpenAI正在开发GPT-5,一种更先进的…...

【面试经典150 | 数学】Pow(x, n)
文章目录 写在前面Tag题目来源题目解读解题思路方法一:快速幂-递归方法二:快速幂-迭代 其他语言python3 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主…...

封装比较好的登录页面
封装比较好的登录页面 只在setup()函数中写流程,将逻辑代码抽离出来 <template><div class"wrapper"><img class"wrapper__img" srchttp://www.dell-lee.com/imgs/vue3/user.png /><div class"wrapper__input"&…...

如何使用Flask request对象处理请求
在 Flask 中,request 对象是处理 HTTP 请求的重要工具之一。它提供了许多属性和方法,可以帮助我们获取请求的相关信息和数据。本文将向你介绍 request 对象的常用方法以及如何在 Flask 应用程序中使用它。 1. 获取请求方法 首先,让我们看一…...
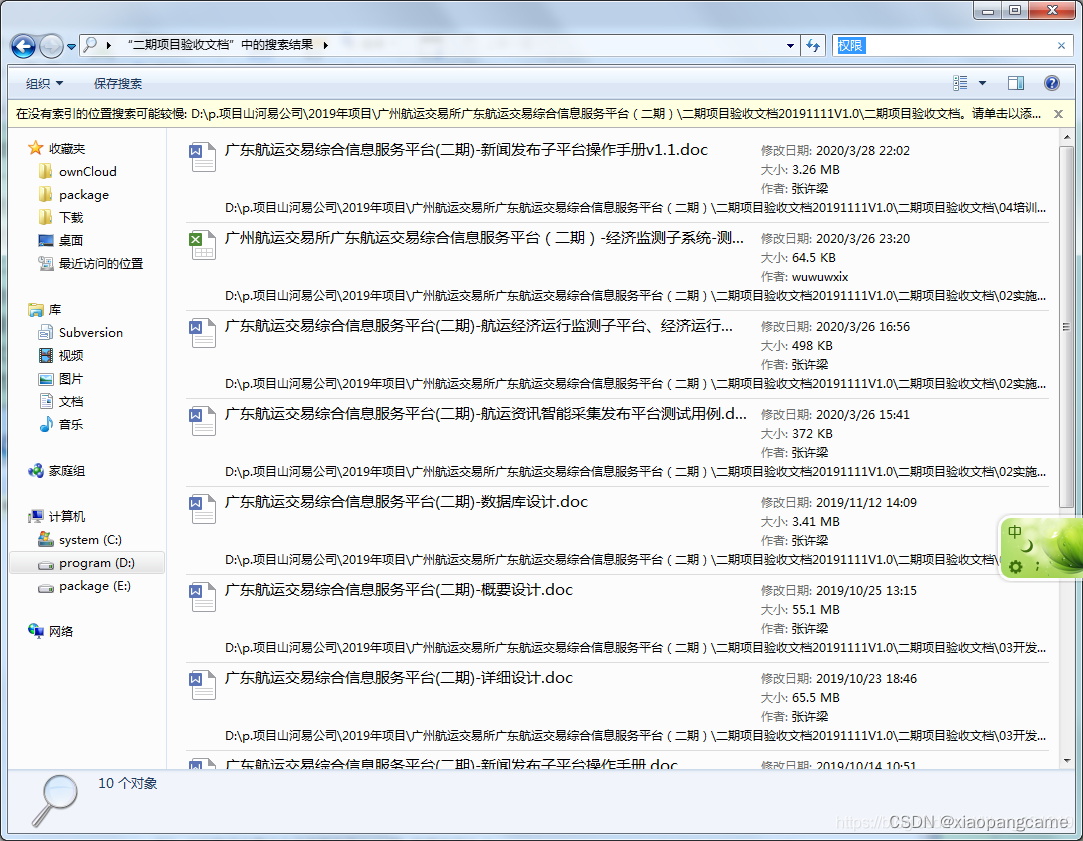
快速搜索多个word、excel等文件中内容
如何快速搜索多个word、excel等文件中内容 操作方法 以win11系统为介绍对象。 首先我们打开“我的电脑”-->“文件夹选项”-->“搜索”标签页,在“搜索内容”下方选择:"始终搜索文件名和内容(此过程可能需要几分钟)"。然后…...
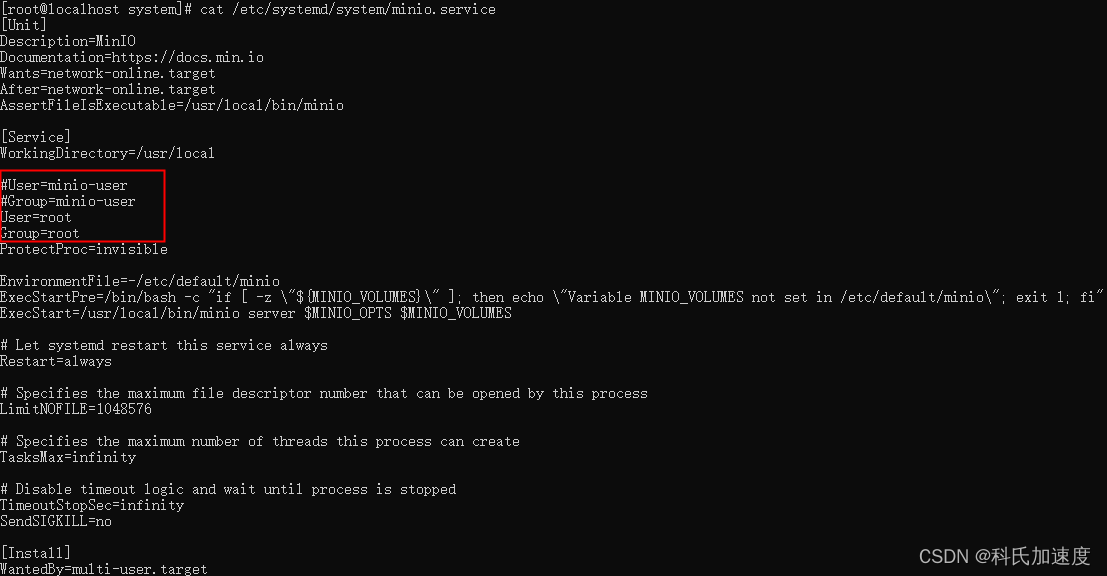
Minio安装
环境 centos8,关闭防火墙 minio-20231101183725版本 参考官网:部署 MinIO:单节点单硬盘 — 适用于 Linux 的 MinIO 对象存储 单例 下载rpm,用中国镜像 wget https://dl.minio.org.cn/server/minio/release/linux-amd64/arch…...
Spring初识
未来的几周时间,大概率我会更新一下Spring家族的一些简单知识。而什么是Spring家族,好多同学还不是很清楚,我先来简单介绍一下吧: 所谓Spring家族,它其实就是一个框架,是基于Servlet再次进行封装的内容。为…...

2023全新付费进群系统源码 带定位完整版 附教程
这源码是我付费花钱买的分享给大家,功能完整。 搭建教程 Nginx1.2 PHP5.6-7.2均可 最好是7.2 第一步上传文件程序到网站根目录解压 第二步导入数据库(58soho.cn.sql) 第三步修改/config/database.php里面的数据库地址 第四步修改/conf…...

C# LINQ使用介绍
LINQ(Language-Integrated Query)是C#语言的一个强大特性,它允许开发者用声明性的方式查询和操作数据。LINQ提供了一致的查询体验,无论是操作内存中的对象(如数组或集合),还是操作外部数据源&am…...

【c++】——类和对象(中)——实现完整的日期类(优化)万字详细解疑答惑
作者:chlorine 专栏:c专栏 赋值运算符重载()()():实现完整的日期类(上) 我走的很慢,但我从不后退。 【学习目标】 日期(- - --)天数重载运算符 日期-日期 返回天数 对日期类函数进行优化(不符合常理的日期,负数,const成员)c中重载输入cin和输…...

开源与闭源:大模型时代的技术交融与商业平衡
一、开源和闭源的优劣势比较 1.1 开源 优势: 1.技术共享与吸引人才: 开源促进了技术共享,吸引了全球范围内的人才参与大模型的发展,形成了庞大的开发者社区。 2.推动创新: 开源模式鼓励开发者共同参与,推动…...

C#开发的OpenRA游戏之属性BodyOrientation(6)
C#开发的OpenRA游戏之属性BodyOrientation(6) 在顶层定义里会发现这个属性: ^SpriteActor: BodyOrientation: QuantizeFacingsFromSequence: RenderSprites: SpriteActor是用来定义角色的基本属性,它的第一个属性就是BodyOrientation,这个属性主要用来描述角色的身体的…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...
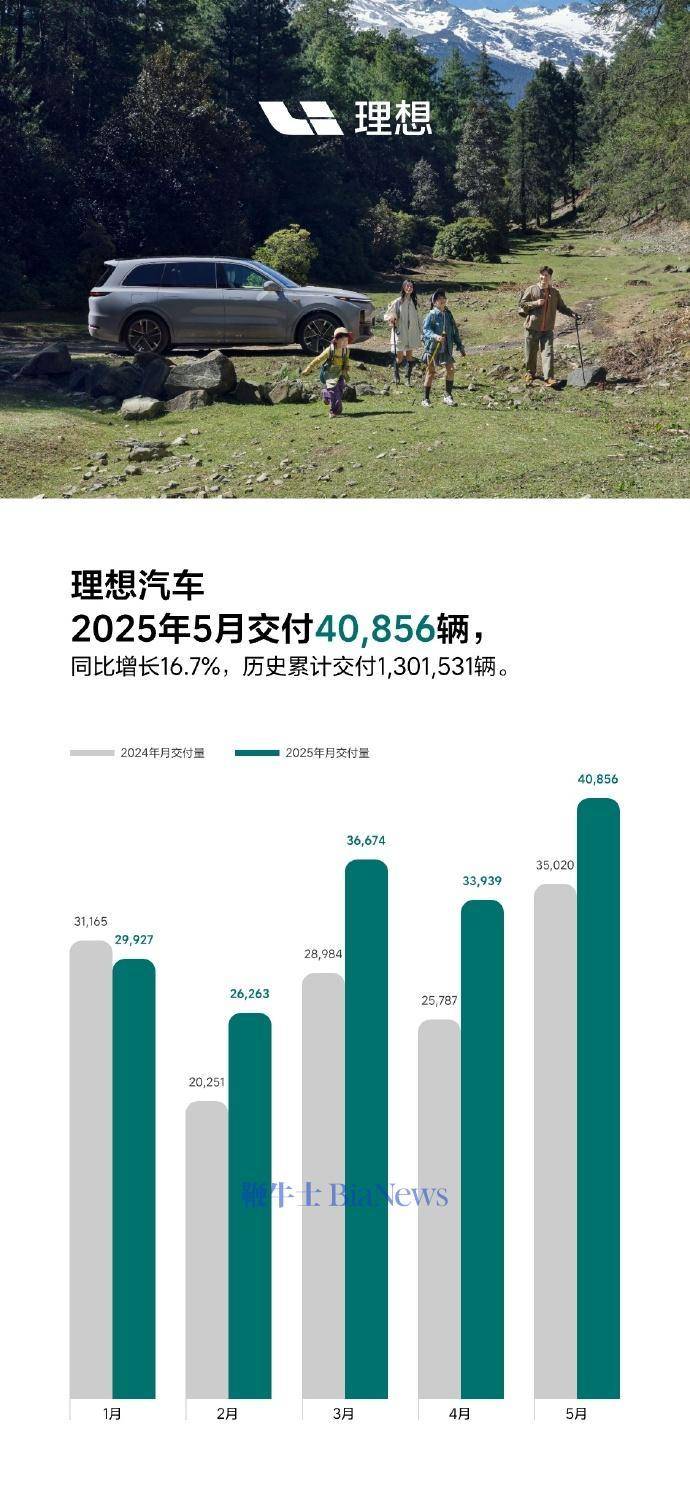
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
