【面试经典150 | 数学】Pow(x, n)
文章目录
- 写在前面
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:快速幂-递归
- 方法二:快速幂-迭代
- 其他语言
- python3
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【快速幂】
题目来源
50. Pow(x, n)

题目解读
计算一个数的整数次幂。
解题思路
计算一个数的整数次幂有朴素的方法和二分的方法,朴素的方法就是一个一个的乘起来,时间复杂度为 O ( n ) O(n) O(n), n n n 指的是幂指数。接下来要介绍的是二分法,即快速幂,有递归和迭代两种解法。建议读者掌握快速幂的方法,该方法是一些题目计算的一个重要工具。
方法一:快速幂-递归
写递归代码的一个重要思想,坚信自己写的递归就是对的,可以直接调用。用快速幂求解一个数的整数次幂是一种二分的递归,比如我们要计算 x n x^n xn 时:
- 我们可以先递归的计算 y = x ⌊ n / 2 ⌋ y = x^{\lfloor{n / 2} \rfloor} y=x⌊n/2⌋;
- 如果
n是偶数,那么 x n = y 2 x^n=y^2 xn=y2;如果 n n n 是奇数,那么 x n = y 2 × x x^n=y^2 \times x xn=y2×x; - 递归的边界(递归出口)为
n = 0,因为任意数的0次方均为1。
实现代码
class Solution {
public:double quickMul(double x, long long N) {if (N == 0) return 1.0;double y = quickMul(x, N/2);return N & 1 ? y * y * x : y * y;}double myPow(double x, int n) {long long N = n;return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);}
};
复杂度分析
时间复杂度: O ( l o g n ) O(logn) O(logn), n n n 为幂指数。因为每次递归都会使指数减少一半,因此递归的层数为 O ( l o g n ) O(logn) O(logn),时间复杂度也为 O ( l o g n ) O(logn) O(logn)。
空间复杂度: O ( l o g n ) O(logn) O(logn)。
方法二:快速幂-迭代
在完全理解了递归的思想后,会发现递归真简单,但是完全理解递归之前还是觉得迭代简单容易理解。现在就来看看迭代解法。
我们依旧是使用二分来计算幂:
- 如果指数为奇数,则累乘答案,即
res *= x; - 然后更新
x *= x; - 最后返回
res即可。
实现代码
class Solution {
public:double quickMul(double x, long long n) {double res = 1.0;for (; n; n /= 2) {if (n & 1) {res *= x;}x *= x;}return res;}double myPow(double x, int n) {long long N = n;return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);}
};
复杂度分析
时间复杂度: O ( l o g n ) O(logn) O(logn), n n n 为幂指数。
空间复杂度: O ( 1 ) O(1) O(1)。
其他语言
python3
在 Python 中,可以使用内置的 pow 函数来进行快速幂的计算。pow 函数的签名如下:
pow(x, y, z=None, /)
其中,x 为底数,y 为指数,z 为模数(如果指定了模数,则返回 x**y % z)。这个函数的时间复杂度较低,因为它采用了快速幂的算法。
以下是一个示例:
# 计算 2 的 10 次方
result = pow(2, 10)# 输出结果
print(result)
上述代码会输出 1024,即 2 的 10 次方的结果。在这个例子中,pow 函数的参数分别为底数、指数,没有指定模数。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 数学】Pow(x, n)
文章目录 写在前面Tag题目来源题目解读解题思路方法一:快速幂-递归方法二:快速幂-迭代 其他语言python3 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主…...

封装比较好的登录页面
封装比较好的登录页面 只在setup()函数中写流程,将逻辑代码抽离出来 <template><div class"wrapper"><img class"wrapper__img" srchttp://www.dell-lee.com/imgs/vue3/user.png /><div class"wrapper__input"&…...

如何使用Flask request对象处理请求
在 Flask 中,request 对象是处理 HTTP 请求的重要工具之一。它提供了许多属性和方法,可以帮助我们获取请求的相关信息和数据。本文将向你介绍 request 对象的常用方法以及如何在 Flask 应用程序中使用它。 1. 获取请求方法 首先,让我们看一…...
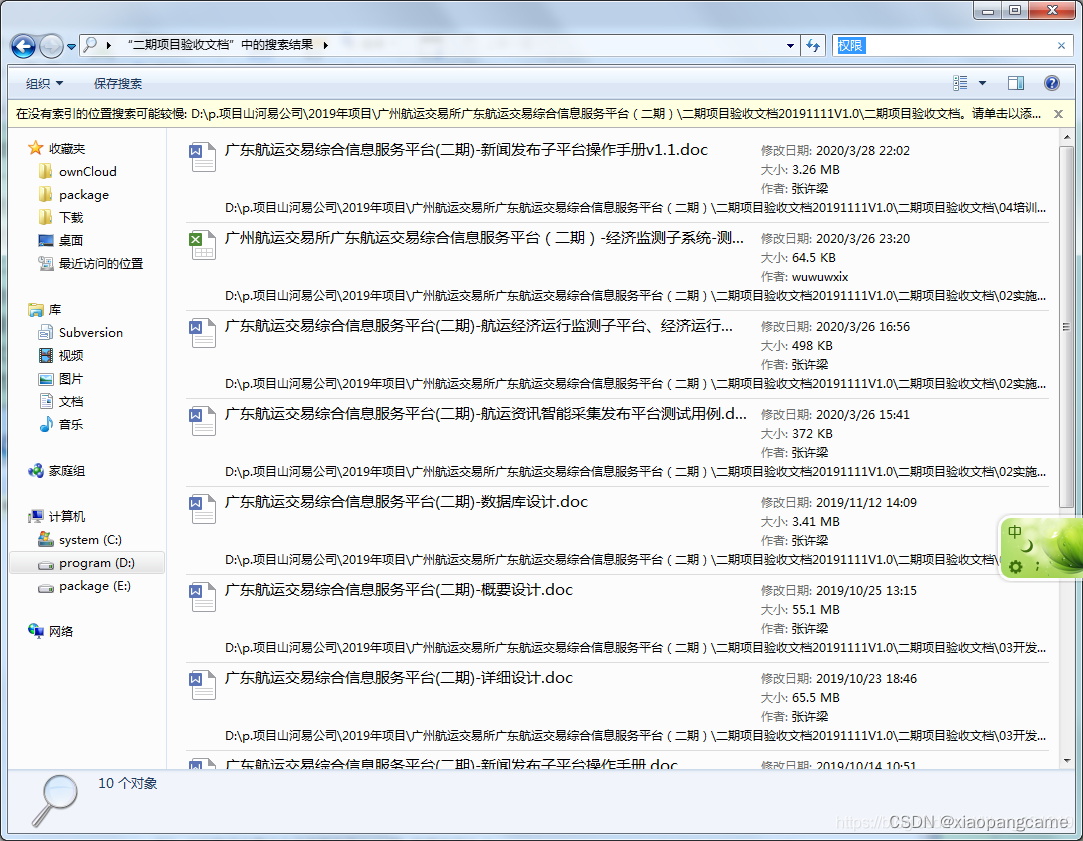
快速搜索多个word、excel等文件中内容
如何快速搜索多个word、excel等文件中内容 操作方法 以win11系统为介绍对象。 首先我们打开“我的电脑”-->“文件夹选项”-->“搜索”标签页,在“搜索内容”下方选择:"始终搜索文件名和内容(此过程可能需要几分钟)"。然后…...
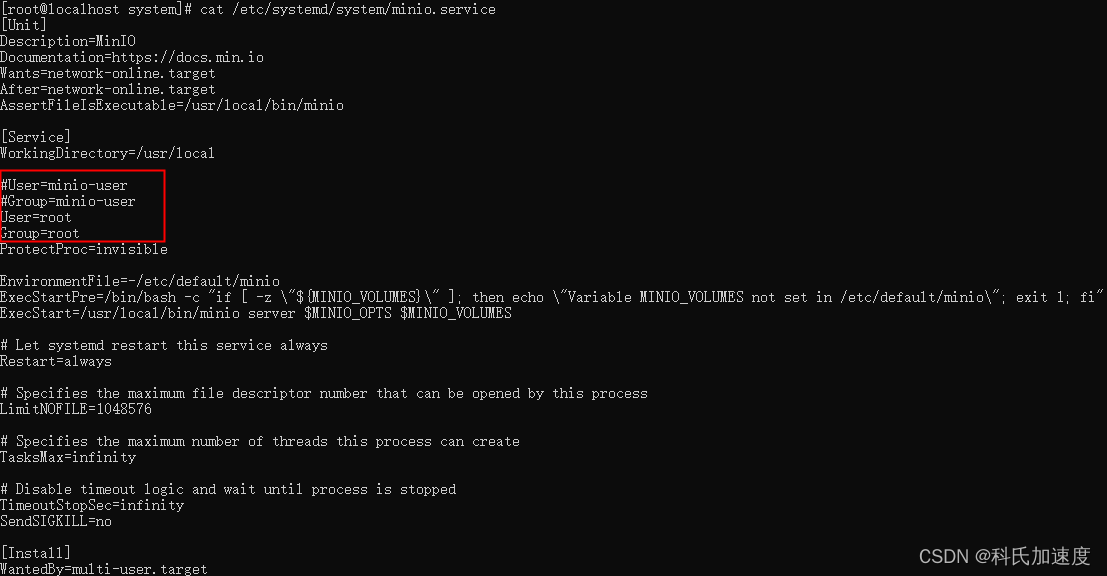
Minio安装
环境 centos8,关闭防火墙 minio-20231101183725版本 参考官网:部署 MinIO:单节点单硬盘 — 适用于 Linux 的 MinIO 对象存储 单例 下载rpm,用中国镜像 wget https://dl.minio.org.cn/server/minio/release/linux-amd64/arch…...
Spring初识
未来的几周时间,大概率我会更新一下Spring家族的一些简单知识。而什么是Spring家族,好多同学还不是很清楚,我先来简单介绍一下吧: 所谓Spring家族,它其实就是一个框架,是基于Servlet再次进行封装的内容。为…...

2023全新付费进群系统源码 带定位完整版 附教程
这源码是我付费花钱买的分享给大家,功能完整。 搭建教程 Nginx1.2 PHP5.6-7.2均可 最好是7.2 第一步上传文件程序到网站根目录解压 第二步导入数据库(58soho.cn.sql) 第三步修改/config/database.php里面的数据库地址 第四步修改/conf…...

C# LINQ使用介绍
LINQ(Language-Integrated Query)是C#语言的一个强大特性,它允许开发者用声明性的方式查询和操作数据。LINQ提供了一致的查询体验,无论是操作内存中的对象(如数组或集合),还是操作外部数据源&am…...

【c++】——类和对象(中)——实现完整的日期类(优化)万字详细解疑答惑
作者:chlorine 专栏:c专栏 赋值运算符重载()()():实现完整的日期类(上) 我走的很慢,但我从不后退。 【学习目标】 日期(- - --)天数重载运算符 日期-日期 返回天数 对日期类函数进行优化(不符合常理的日期,负数,const成员)c中重载输入cin和输…...

开源与闭源:大模型时代的技术交融与商业平衡
一、开源和闭源的优劣势比较 1.1 开源 优势: 1.技术共享与吸引人才: 开源促进了技术共享,吸引了全球范围内的人才参与大模型的发展,形成了庞大的开发者社区。 2.推动创新: 开源模式鼓励开发者共同参与,推动…...

C#开发的OpenRA游戏之属性BodyOrientation(6)
C#开发的OpenRA游戏之属性BodyOrientation(6) 在顶层定义里会发现这个属性: ^SpriteActor: BodyOrientation: QuantizeFacingsFromSequence: RenderSprites: SpriteActor是用来定义角色的基本属性,它的第一个属性就是BodyOrientation,这个属性主要用来描述角色的身体的…...

Linux shell编程学习笔记27:tputs
除了stty命令,我们还可以使用tput命令来更改终端的参数和功能。 1 tput 命令的功能 tput 命令的主要功能有:移动更改光标、更改文本显示属性(如颜色、下划线、粗体),清除屏幕特定区域等。 2 tput 命令格式 tput [选…...
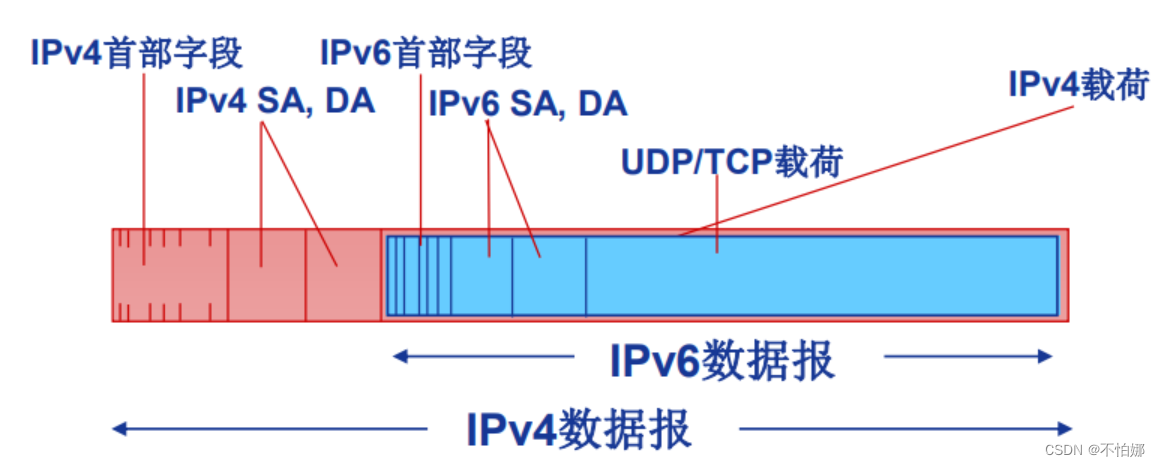
【计算机网络笔记】IPv6简介
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...

c语言-数据结构-堆
目录 一、二叉树 1、二叉树的概念 2、完全二叉树和满二叉树 3、完全二叉树的顺序存储 二、堆 2、堆的概念与结构 3、堆的创建及初始化 4、堆的插入(小堆) 5、堆的删除 6、显示堆顶元素 7、显示堆里的元素个数 8、测试堆的各个功能 9、 实现堆…...

ROS基础—关于参数服务器的操作
1、rosparam list 获取参数服务器的所有参数。 2、rosparam get /run_id 获取参数的值...
Sql Server 2017主从配置之:事务日志传送
使用事务日志传送模式搭建Sql Server 2017主从同步,该模式有一定的延迟,是通过3个不同的定时任务,将主库的日志同步到从库进行恢复来实现数据库同步操作。 环境准备 两台服务器,配置都是8g2核,50g硬盘,操…...

每日OJ题_算法_双指针_力扣283. 移动零+力扣1089. 复写零
力扣283. 移动零 283. 移动零 - 力扣(LeetCode) 难度 简单 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 请注意 ,必须在不复制数组的情况下原地对数组进行操作。 示例…...
WebGl-Blender:建模 / 想象成形 / Blender概念词汇表 / 快捷键
一、理解Blender 欢迎来到Blender!Blender是一款免费开源的3D创作套件。 使用Blender,您可以创建3D可视化效果,例如建模、静态图像,3D动画,VFX(视觉特效)快照和视频编辑。它非常适合那些受益于…...

【C++】【Opencv】cv::warpAffine()仿射变换函数详解,实现平移、缩放和旋转等功能
仿射变换是一种二维变换,它可以将一个二维图形映射到另一个二维图形上,保持了图形的“形状”和“大小”不变,但可能会改变图形的方向和位置。仿射变换可以用一个线性变换矩阵来表示,该矩阵包含了六个参数,可以进行平移…...

WPF实现右键菜单
在WPF中,创建上下文菜单(通常称为“右键菜单”)是通过使用ContextMenu控件来实现的。你可以在XAML中声明上下文菜单,并将其关联到任何FrameworkElement。以下是如何在WPF中实现上下文菜单的基本步骤: 1. 在XAML中定义…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

【AI News | 20250609】每日AI进展
AI Repos 1、OpenHands-Versa OpenHands-Versa 是一个通用型 AI 智能体,通过结合代码编辑与执行、网络搜索、多模态网络浏览和文件访问等通用工具,在软件工程、网络导航和工作流自动化等多个领域展现出卓越性能。它在 SWE-Bench Multimodal、GAIA 和 Th…...
