c语言-数据结构-堆

       

目录

一、二叉树

1、二叉树的概念

 2、完全二叉树和满二叉树

3、完全二叉树的顺序存储

二、堆

2、堆的概念与结构

3、堆的创建及初始化

4、堆的插入（小堆）

 5、堆的删除

6、显示堆顶元素

7、显示堆里的元素个数

8、测试堆的各个功能

9、 实现堆排序

三、TOP-K的实现

结语：

---

前言：

        堆是数据结构中是很重要的一个知识点，通常用于实现堆排序， 比如在生活中我们要算出考试成绩的前十名，或者游戏排名的前一百名，这种场景下就用到堆排序了。堆其实是相同类型元素的集合，通常用数组的形式表示一个堆，数组内的所有元素都按照完全二叉树的形式进行存储，这时候又引出了二叉树的概念，只要明白了完全二叉树的概念就明白了什么是堆，因此下面先介绍二叉树的基本概念。

一、二叉树

1、二叉树的概念

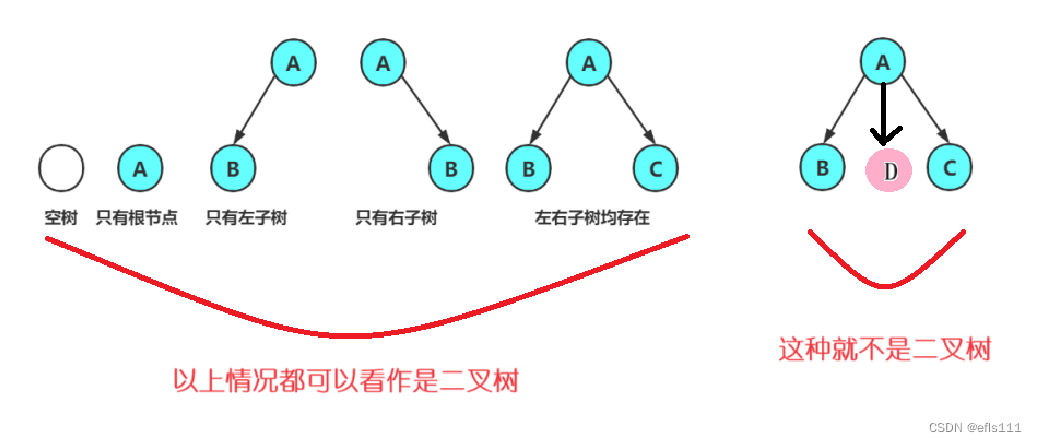
        二叉树的根节点由一个左子树和一个右子树构成，也就是每一个结点可以少于两个孩子结点但是不能多于两个孩子结点，示意图如下：

        如上图，D可以是A的孩子结点，同时D也可以是H的父母节点，D同时也是E的兄弟节点，一个结点可以拥有多重身份。如果一棵树中的任意一个结点有超过2个孩子结点那么该树就不是一个二叉树，二叉树的其他情况如下：

 2、完全二叉树和满二叉树

        一颗二叉树的每一层的结点都是满的，将该二叉树称为满二叉树，完全二叉树则是在满二叉树的概念上引申而来的，即满二叉树的最后一层的结点可以不是满的，但是二叉树中的所有结点从左到右必须是按照顺序排序的，示意图如下：

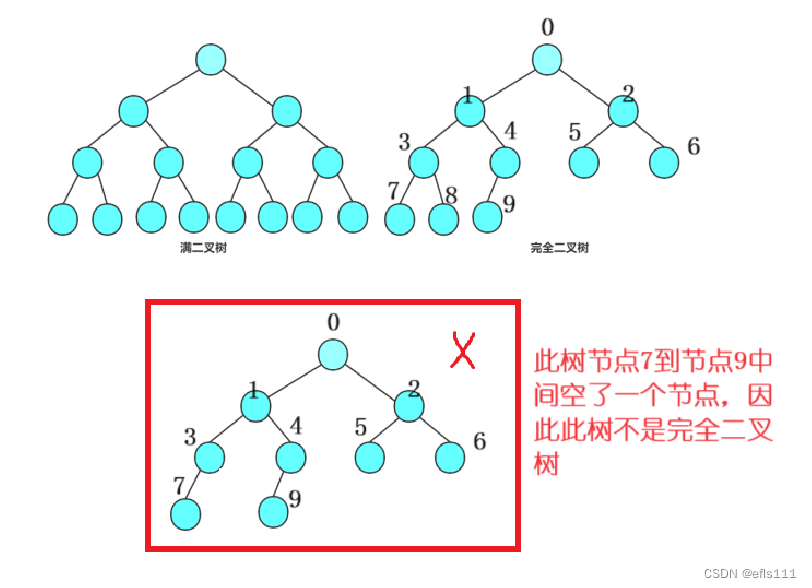
         因此可以看出完全二叉树的一个特点：即每个节点必须是按照顺序进行存储的，即完全二叉树具有顺序性。

3、完全二叉树的顺序存储

        我们知道数组是一块连续的空间，而且数组里的元素都是“紧挨着”的，即不存在第一个元素和第三个元素中间空了位置不存储任何数据，这么做不符合逻辑也很浪费空间。由此看来，数组和完全二叉树的特点非常相似。

        因此一个完全二叉树可以用数组的形式表示出来，只要是一个数组就是一个完全二叉树。并且有了父母结点的下标就可以找到他的孩子结点，有了孩子的结点就能找到其父母结点的下标。 

        比如有了结点B的下标，可以找到他的左右两个孩子结点的下标：左孩子D的下标=B的下标*2+1，右孩子E的下标=B的下标*2+2。

        B的父母结点A坐标=（B坐标-1）/2。

二、堆

2、堆的概念与结构

       堆是一个完全二叉树，但是他在完全二叉树的基本要求上增加了以下条件：树里任意一个父母结点都大于等于（或小于等于）他们的孩子结点，因此堆分为两种情况：大堆和小堆。

        大堆：从根节点开始，从上至下每个父亲结点必须大于他的两个孩子结点。

        小堆：从根节点开始，从上至下每个父亲结点必须小于他的两个孩子结点。

        示意图如下：

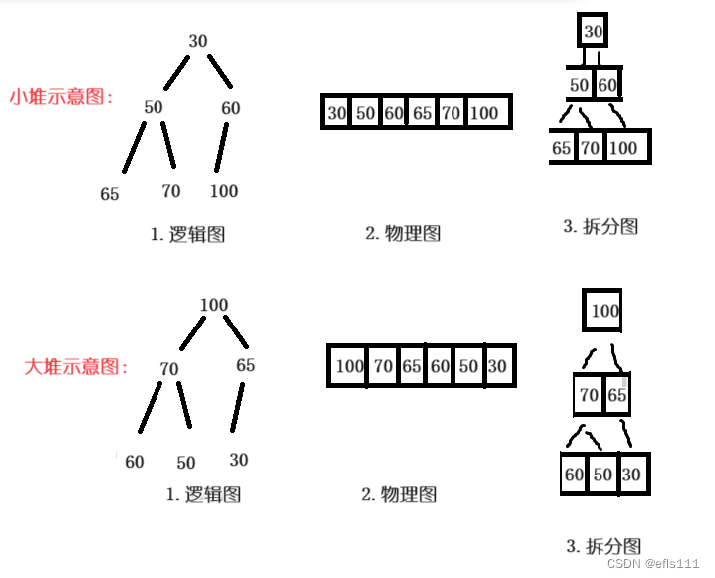
        因此从以上的分析来看，可以得出以下结论：数组其实就可以看成是一个完全二叉树，但是不一定是堆，但是是堆就一定是完全二叉树。而且即使是小堆也不一定是升序，大堆也不一定是降序（这里只是偶然）。当然，有序的数组一定是堆。 

        接下来用代码建立一个小堆。

3、堆的创建及初始化

        从以上得知，堆的本质是数组，因此堆的创建代码如下：

typedef int HeapDataType;//int类型重定义
typedef struct Heap
{HeapDataType* arr;//指针arr，即数组名表示数组的首地址int size;//数组的元素个数int capacity;//数组的容量
}Heap;

         堆初始化代码如下：

void HeapInit(Heap* php)//初始化
{assert(php);php->arr = NULL;//置为空php->size = 0;//刚开始没有元素因此为0php->capacity = 0;
}

4、堆的插入（小堆）

        原理就是把数据插入到数组中，所以在数组的末尾处添加数据即可，但是单单的插入数据并不能满足大堆和小堆的条件，因此每插入一个数据都要对数组进行调整，以便然数组满足小堆的条件。

        然而从数组的末尾处插入元素，从完全二叉树的角度来看，就是从树的最后一个结点插入元素，因此对数组进行调整其实就是调整插入元素与其父母结点的一个大小关系。插入最后一个结点的时候进行对树的调整的，该调整法称为向上调整法。向上调整示意图如下：

        建小堆和向上调整法代码如下：

void Swap(HeapDataType* p1, HeapDataType* p2)//交换函数
{int temp = *p1;*p1 = *p2;*p2 = temp;
}void AdjustUp(HeapDataType* arr, int child)//向上调整函数
{assert(arr);int parent = (child - 1) / 2;//求出父母结点下标while (child > 0)//等于0才结束循环说明是最坏情况与根交换{if (arr[child] < arr[parent])//如果孩子小则与父母交换{Swap(&arr[child], &arr[parent]);//让孩子结点和父母结点交换child = parent;//让原先的父母结点变成孩子结点继续调整parent = (child - 1) / 2;//找到原先父母结点的父母结点}else//表示没有达到最坏情况{break;}}
}void HeapPush(Heap* php, HeapDataType x)//入堆
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;//三目法更新容量HeapDataType* temp = (HeapDataType*)realloc(php->arr, sizeof(HeapDataType) * newcapacity);//开辟以及扩容空间if (temp == NULL){perror("HeadFush");return;}php->arr = temp;//让arr指向新的空间php->capacity = newcapacity;//更新容量}php->arr[php->size] = x;//入堆php->size++;//更新sizeAdjustUp(php->arr, php->size - 1);//向上调整堆
}

 5、堆的删除

        堆的删除一般是将堆顶的元素删除，堆顶的元素即是下标为0的元素，也就是数组的第一个元素，如果将堆顶的元素直接删除，堆肯定会发生变化，会导致该数组不再是堆了，因此进行堆的删除的同时要调整堆。因为是堆顶的元素发生了改变，所以从堆顶的位置往下调整，进行向下调整。向下调整堆的具体逻辑如下图：

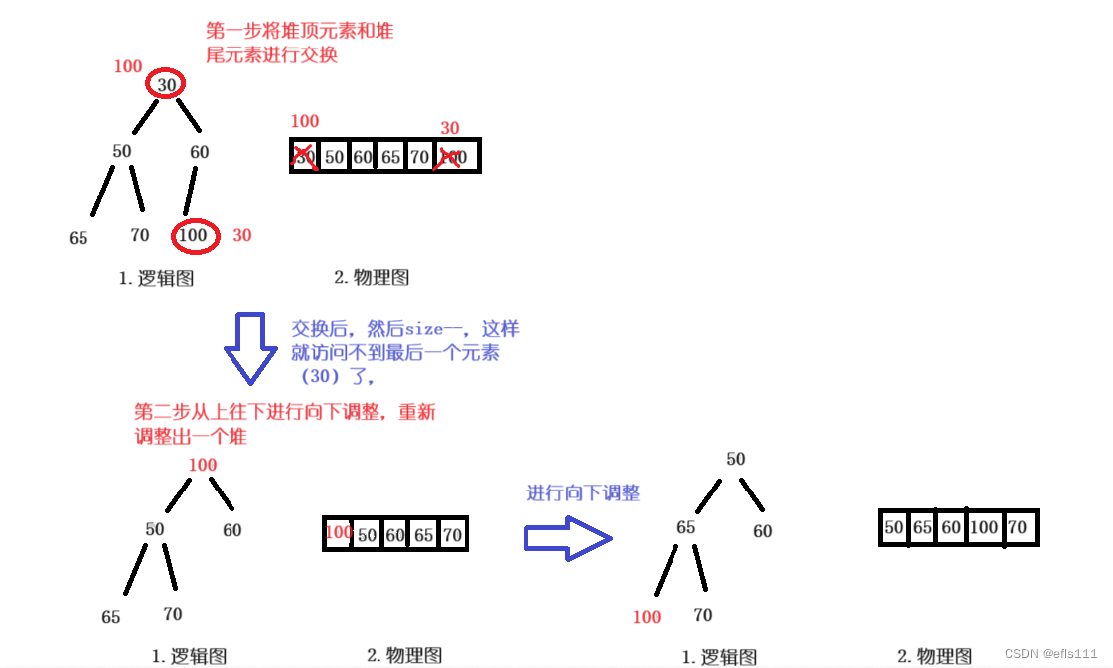
        向下调整法思路：把堆顶元素和堆尾元素进行交换，然后从堆顶处开始向下调整，一直调整到元素30的前一个元素。让堆顶元素跟他的两个孩子中最小的孩子进行比较，如果他的孩子比他小则他们俩进行交换，如此循环往下比较，直到树的最后一层。注意：此时的元素30是不参与调整的。

        堆的删除及向下调整法代码如下： 

bool Empty(Heap* php)//判空函数
{assert(php);return php->size == 0;//为空即返回真
}void AdjustDown(HeapDataType* arr, int size, int parent)//向下调整堆
{assert(arr);int child = parent * 2 + 1;//找出其左孩子while (child < size)//若孩子的下标已经超出了数组元素个数，说明数组已经是堆{if ((child + 1 < size) && arr[child + 1] < arr[child])//此判断可以找出最小的孩子{child++;}if (arr[child] < arr[parent])//若孩子小于父母则交换{Swap(&arr[child], &arr[parent]);parent = child;//进行往下遍历child = parent * 2 + 1;}else{break;}}
}void HeapPop(Heap* php)//删除堆顶
{assert(php);assert(!Empty(php));//堆为空则Empty函数返回真，对其取非，则堆为空assert生效Swap(&php->arr[0], &php->arr[php->size - 1]);//交换函数php->size--;szie需要--因为此时的size是最后一个元素的后一个位置AdjustDown(php->arr, php->size, 0);//向下调整堆，从堆顶开始到堆尾结束
}

6、显示堆顶元素

        显示堆顶元素就很简单了，堆顶表示的是数组的首元素，首元素下标为0，显示堆顶代码如下：

HeapDataType HeapTop(Heap* php)//展示堆顶
{assert(php);return php->arr[0];
}

7、显示堆里的元素个数

        堆的大小就是size的值，因为每次赋值后size都会++，所以刚好可以用size表示元素个数，代码如下：

int HeapSize(Heap* php)//堆的元素的总数
{assert(php);return php->size;
}

8、测试堆的各个功能

       以上介绍了那么多的功能，现在对这些功能进行测试，代码如下：

void test1()
{Heap hp;//创建堆的结构体变量HeapInit(&hp);//初始化int a[] = { 7,8,3,5,1,9,4,5 };for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);//把数组a里的元素入进堆里}printf("size:%d\n", HeapSize(&hp));//打印堆里元素总数int i = 0;while (!Empty(&hp))//循环打印出堆里的所有元素{printf("%d ",HeapTop(&hp));//打印堆顶的元素HeapPop(&hp);//删除堆顶元素}HeapDestroy(&hp);//释放堆
}int main()
{test1();return 0;}

        运行结果：

        可以看到打印出来的结果是一个有序的数组，原因是每次打印堆顶的元素然后就删除该堆顶元素并且进行了向下调整，调整完之后此时堆顶元素就是第二小的元素，所有才能打印出有序的序列。 

9、 实现堆排序

        以上的测试可以发现是在数组arr中进行的，但是原数组a并没有受到改变，若想实现排序，则必须在原数组内对原数组里的顺序进行排序。

        堆排序代码如下：

void test2()//堆排序
{Heap hp;HeapInit(&hp);//初始化int arr[] = { 7,8,3,5,1,9,4,5 };//创建一个数组int k = sizeof(arr) / sizeof(int);//对原数组进行建堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, k, i);//}//建完堆之后不一定是有序的数组，因此还需要对其进行调整int end = sizeof(arr) / sizeof(int) - 1;while (end > 0){Swap(&arr[0], &arr[end]);//堆顶元素与堆尾元素进行交换AdjustDown(arr, end, 0);//向下调整到堆尾的前一个元素end--;//堆尾下标--，准备下一次的交换}//打印for (int i = 0; i < k; i++){printf("%d ", arr[i]);}
}int main()
{test1();return 0;}

        首先在原数组a中进行建堆，建完堆之后不代表数组a就是有序的，因此还需要对其进行调整，我们可以保证的是数组在建完堆之后堆顶的元素是最小的，因此把堆顶元素跟堆里的最后一个元素进行交换（用end表示堆尾的下标），然后从堆顶开始向下调整到end的前一个位置结束调整，思路与堆的删除相似。

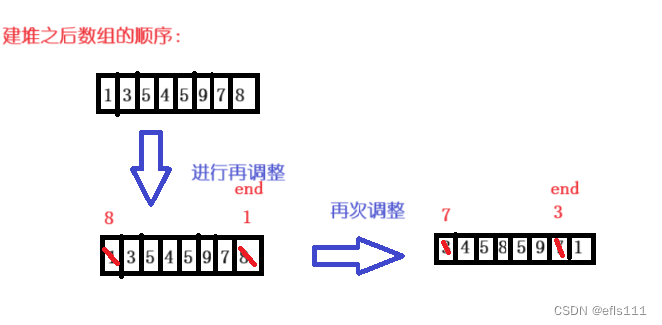
        从上图分析来看，最后会得到一组降序的数组，因此得出结论建立小堆得到的是降序，而建立大堆得到的是升序。

三、TOP-K的实现

        一般我们要查询某个专业的前十名，或者前世界500强的公司有哪些的时候都会用到TOP-K来解决，当要搜索的范围很大的时候，用正常的排序是难以解决的，比如从10亿个数中求出前五个最大的数，这时候如果把10亿个数排好序则要耗费大量的内存，很明显排序的办法不行。

        这时候就需要堆来解决了，可以先建立一个5个数字的小堆，然后从这10个数中不断的取出数据跟堆顶元素进行比较，如果比堆顶元素大则替换堆顶元素然后再进行向下调整堆，最后堆里的5个元素就10亿中最大的5个元素。用堆解决的优势在于这10亿个数不需要全部拿到内存中，而是存在磁盘里的文件中就可以进行对比了，需要文件操作函数来实现。

        这里我就用1000个数作为测试用例，TOP-K代码如下：

void CreatData()//创造数据
{int n = 1000;//这里我们只创建1000个数用来测试srand(time(0));//生成随机数FILE* fin = fopen("data.txt", "w");//以写的方式打开文件if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; i++){int x = rand() % 10000;//生成10000以内的随机值fprintf(fin, "%d\n", x);//把这些值写进文件中}fclose(fin);//关闭文件fin = NULL;
}void TOP_K(int k)//选出5个最大的数
{FILE* fin = fopen("data.txt", "r");//以读的方式打开文件if (fin == NULL){perror("fopen error");return;}//创建数组int* arr = (int*)malloc(sizeof(int)*k);if (arr == NULL){perror("malloc error");return;}//倒数据for (int i = 0; i < k; i++){fscanf(fin, "%d", arr + i);//把文件里的前五个数给到数组arr，准备建堆}//建小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, k, i);//向下调整建立小堆}//TOP-Kint val = 0;//创建val变量while (!feof(fin))//遍历文件内容{fscanf(fin, "%d", &val);//把文件里的值以%d的形式给到val变量if (val > arr[0])//如果val的值大于堆顶元素{arr[0] = val;//将val的值赋给堆顶AdjustDown(arr, k, 0);//并且重新向下调整堆，保证数组是一个堆}}//打印数组for (int i = 0; i < k; i++){printf("%d ", arr[i]);}fclose(fin);//关闭文件fin = NULL;
}int main()
{CreatData();//创建数据TOP_K(5);//TOP-K实现return 0;}

        创建文件数据的结果：

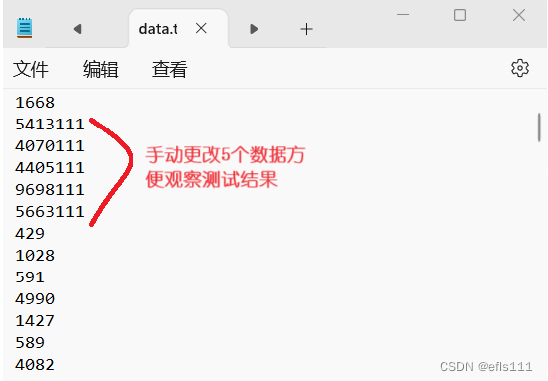
        运行结果：

         从结果可以看到TOP-K确实帮助我们从1000个数中找出了最大的五个数。

结语：

        以上就是关于堆的一系列的解析与延申，堆的重点在于对向上调整和向下调整的理解，这两个调整法才是创建堆的核心。希望本文可以带给你更多的收获，如果本文对你起到了帮助，希望可以动动小指头帮忙点赞👍+关注😎+收藏👌！如果有遗漏或者有误的地方欢迎大家在评论区补充~！！谢谢大家！！(❁´◡`❁)