【算法挨揍日记】day29——139. 单词拆分、467. 环绕字符串中唯一的子字符串
139. 单词拆分
139. 单词拆分
题目描述:
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。

解题思路:
解题代码:
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> hash;for(auto& s : wordDict) hash.insert(s);int n=s.size();vector<bool>dp(n+1);dp[0]=true;s=' '+s;for(int i=1;i<=n;i++){for(int j=i;j>=1;j--){if(dp[j-1]==true&&hash.count(s.substr(j,i-j+1))){dp[i]=true;break;}}}return dp[n];}
};
467. 环绕字符串中唯一的子字符串
467. 环绕字符串中唯一的子字符串
题目描述:
定义字符串 base 为一个 "abcdefghijklmnopqrstuvwxyz" 无限环绕的字符串,所以 base 看起来是这样的:
"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd....".
给你一个字符串 s ,请你统计并返回 s 中有多少 不同非空子串 也在 base 中出现。

解题思路:
解题代码:
class Solution {
public:int findSubstringInWraproundString(string s) {int n=s.size();vector<int>dp(n,1);for(int i=1;i<n;i++){if(s[i]-1==s[i-1]||(s[i-1]=='z'&&s[i]=='a'))dp[i]=dp[i-1]+1;}// 2. 计算每⼀个字符结尾的最⻓连续⼦数组的⻓度int hash[26] = { 0 };for(int i = 0 ; i < n; i++)hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);// 3. 将结果累加起来int sum = 0;for(auto x : hash) sum += x;return sum;}
};相关文章:

【算法挨揍日记】day29——139. 单词拆分、467. 环绕字符串中唯一的子字符串
139. 单词拆分 139. 单词拆分 题目描述: 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。 注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。 解题思路&am…...

YOLOv8-Seg改进:轻量级Backbone改进 | VanillaNet极简神经网络模型 | 华为诺亚2023
🚀🚀🚀本文改进:一种极简的神经网络模型 VanillaNet,支持vanillanet_5, vanillanet_6, vanillanet_7, vanillanet_8, vanillanet_9, vanillanet_10, vanillanet_11等版本,相比较yolov8-seg各个版本如下: layersparametersgradientsGFLOPsvanillanet_521230017523...

解决Requests中使用httpbin服务器问题:自定义URL的实现与验证
问题背景 在使用Python的Requests模块进行单元测试时,可能会遇到无法使用本地运行的httpbin服务器进行测试的问题。这是因为测试脚本允许通过环境变量HTTPBIN_URL指定用于测试的本地httpbin实例,但在某些测试用例中,URL是硬编码为httpbin.or…...
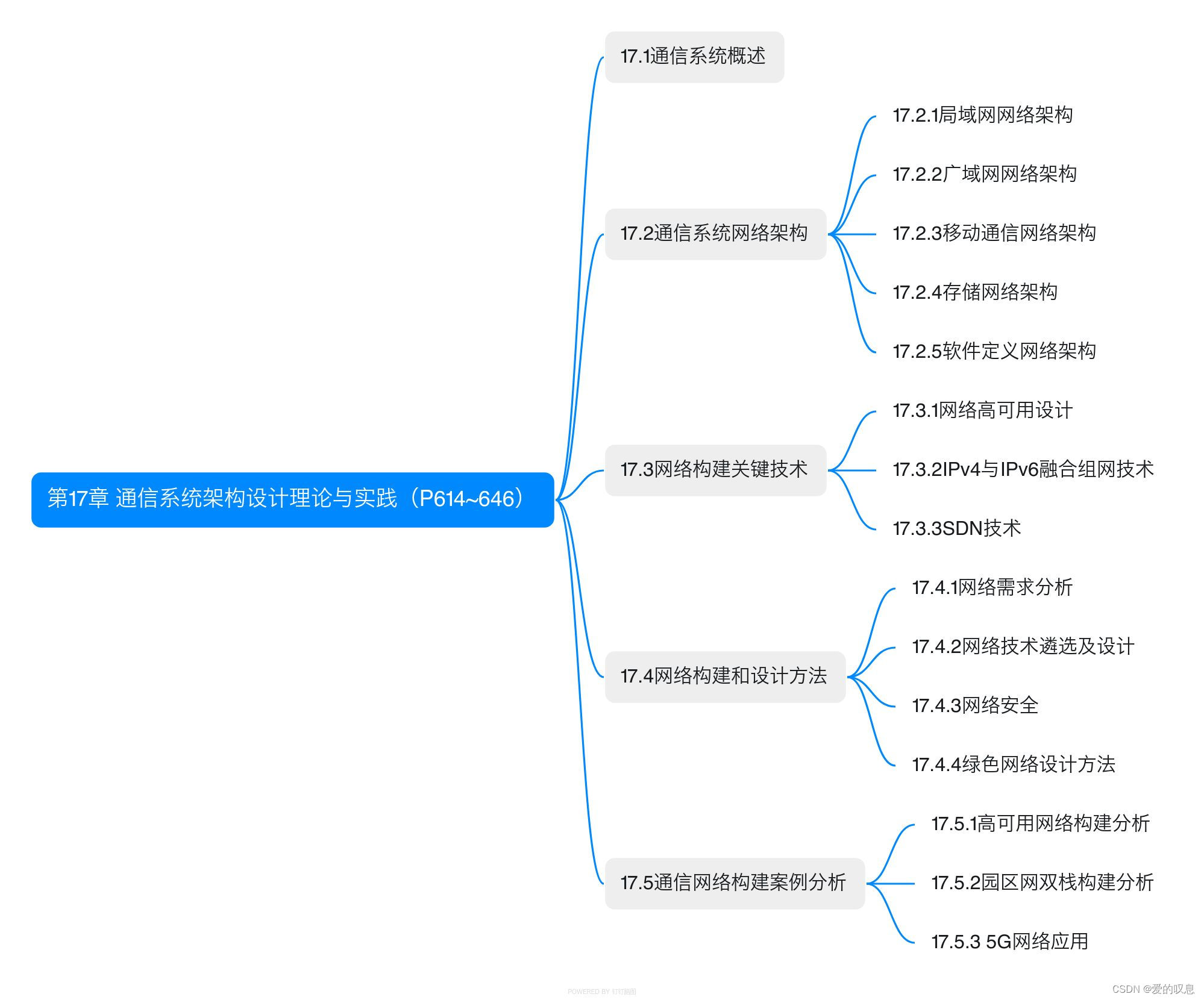
软考-高级-系统架构设计师教程(清华第2版)【第17章 通信系统架构设计理论与实践(P614~646)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第17章 通信系统架构设计理论与实践(P614~646)-思维导图】 课本里章节里所有蓝色字体的思维导图...
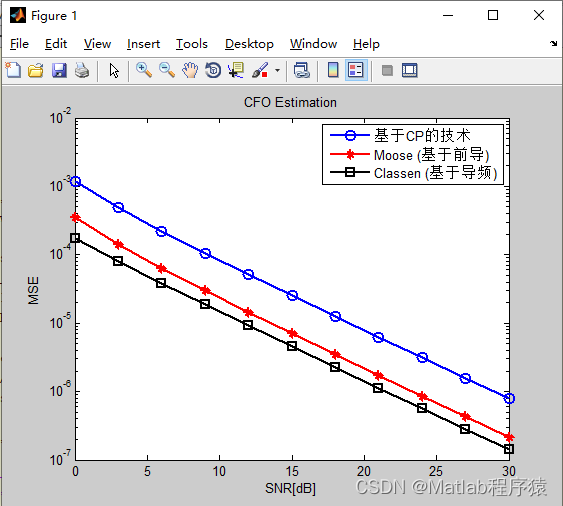
【MATLAB源码-第82期】基于matlab的OFDM系统载波频移偏差(CFO)估计,对比三种不同的方法。
操作环境: MATLAB 2013b 1、算法描述 正交频分复用(OFDM)系统中的载波频率偏移(CFO)估计是一项关键技术,用于确保数据传输的准确性和效率。CFO通常由于振荡器频率不匹配和多普勒频移引起。不同的CFO估计…...
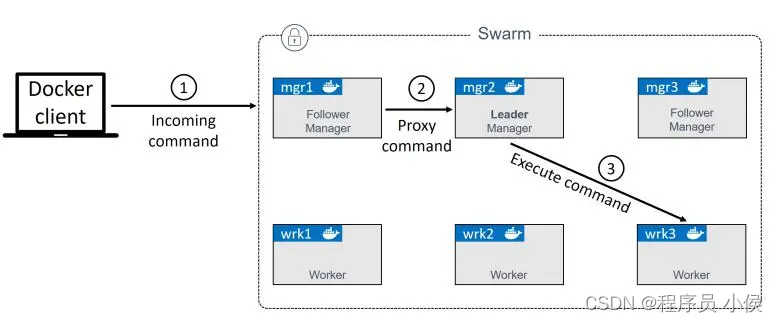
Docker Swarm: 容器编排的力量和优势深度解析
文章目录 Docker Swarm的核心概念1. 节点(Node)2. 服务(Service)3. 栈(Stack) 使用Docker Swarm1. 初始化Swarm2. 加入节点3. 创建服务4. 扩展和缩减服务5. 管理栈6. 管理服务更新 Docker Swarm的优势深度解…...
调整Windows键盘上只能看到拼音而无法看到实际的文本以及关闭输入法悬浮窗方法
一、输入法设置 如果您在键盘上只能看到拼音而无法看到实际的文本,这可能是因为您的输入法设置为中文拼音输入法或其他仅显示拼音的输入法。 要解决这个问题,您可以尝试以下方法: 1. 切换输入法:按下 Shift Alt 组合键或 Wind…...

【微软技术栈】C#.NET 中的管道操作
C#.NET 管道为进程间通信提供了平台。 管道分为两种类型: 匿名管道。 匿名管道在本地计算机上提供进程间通信。 与命名管道相比,虽然匿名管道需要的开销更少,但提供的服务有限。 匿名管道是单向的,不能通过网络使用。 仅支持一个服…...

Python学习笔记--进程
进程 Python 中的多线程其实并不是真正的多线程,如果想要充分地使用多核 CPU 的资源,在 Python 中大部分情况需要使用多进程。 Python 提供了非常好用的多进程包 multiprocessing,只需要定义一个函数,Python 会完成其他所有事情。 借助这个包,可以轻松完成从单进程到并…...
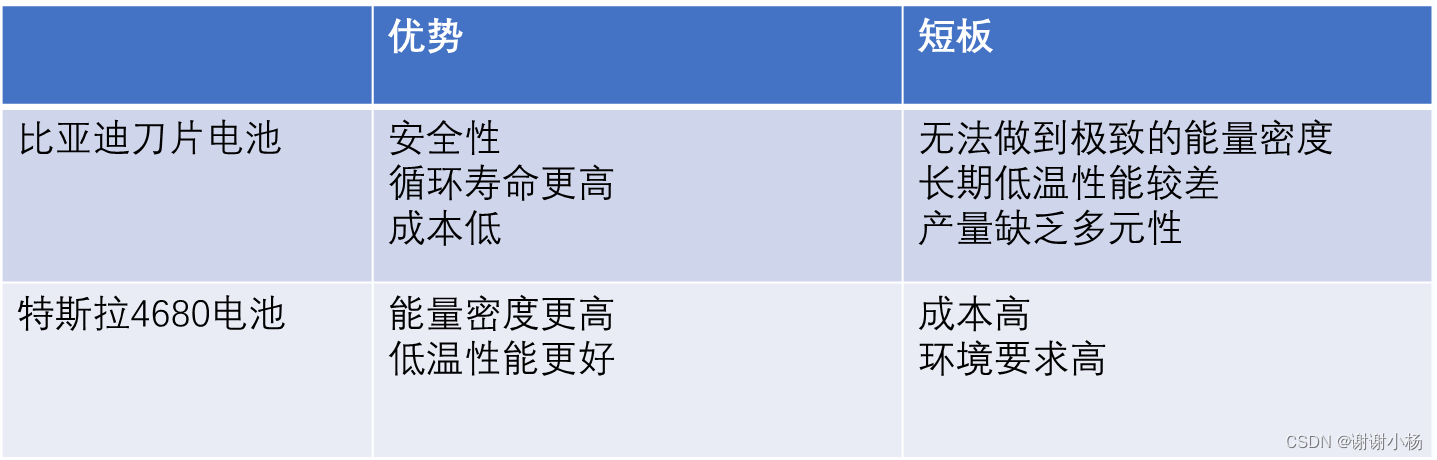
比亚迪刀片电池与特斯拉4680电池比较
1 电池材料 比亚迪刀片电池采用的磷酸铁锂LFP(LiFePO4),特斯拉的4680电池采用的三元锂。 磷酸铁锂:循环寿命长,安全性能好,价格低廉,但是能量密度低,导电性能差,低温表现…...

在写windows C++代码的时候,从代码安全角度考虑,我们应该注意什么?
在写windows C代码的时候,从代码安全角度考虑,我们应该注意什么?分别是:输入验证、内存管理、错误处理、并发和线程安全、使用安全的API、避免使用不安全的函数、最小权限原则。 一、输入验证 1. 用户输入验证 #include <io…...
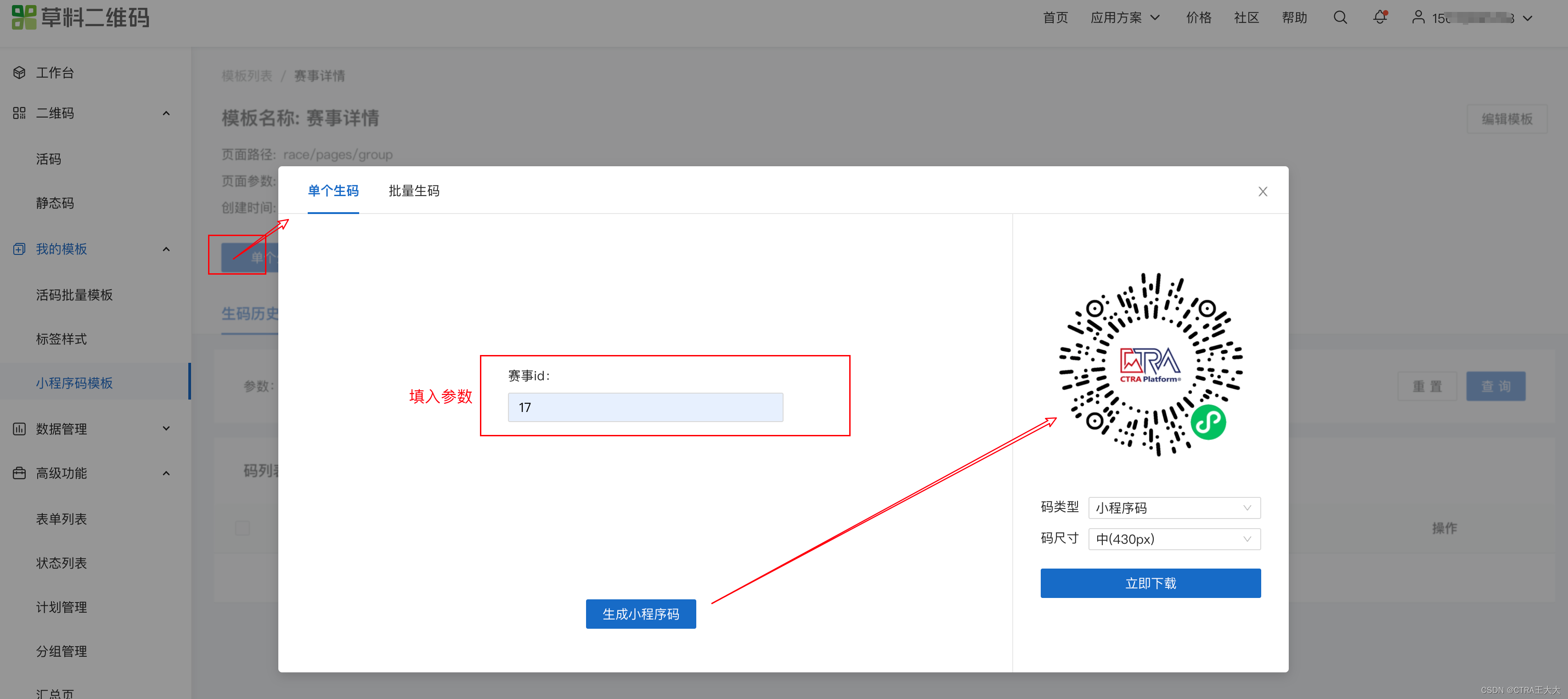
【草料】uni-app ts vue 小程序 如何如何通过草料生成对应的模块化二维码
一、查看uni-app项目 1、找到路径 可以看到项目从 src-race-pages-group 这个使我们目标的查询页面 下面我们将这个路径copy到草料内 2、找到进入页面入参 一般我们都会选择 onload() 函数下的入参 这里我们参数的是 id 二、草料 建议看完这里的教程文档 十分清晰!…...

CMS与FullGC
JVM中的CMS(Concurrent Mark Sweep)GC和Full GC(Full Garbage Collection)是两种不同的垃圾回收算法。 CMS GC:CMS GC是一种并发的垃圾回收算法,它在运行期间与应用程序线程并发工作,尽可能减少…...

一款.NET开源的小巧、智能、免费的Windows内存清理工具 - WinMemoryCleaner
前言 我们在使用Windows系统的时候经常会遇到一些程序不会释放已分配的内存,从而导致电脑变得缓慢。今天给大家推荐一款.NET开源的小巧、智能、免费的Windows内存清理工具:WinMemoryCleaner。 使用Windows内存清理工具来优化内存,这样不必浪…...
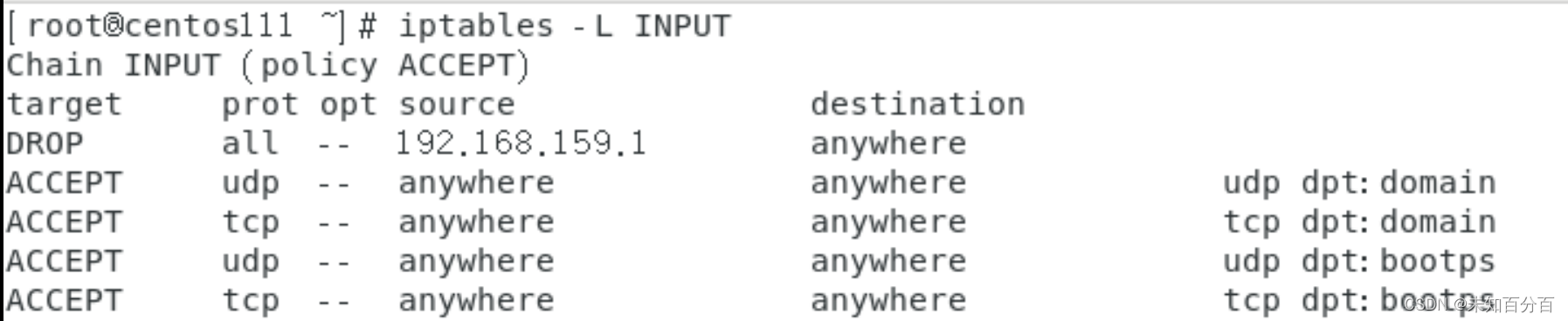
iptables详解:链、表、表链关系、规则的基本使用
目录 防火墙基本概念 什么是防火墙? Netfilter与iptables的关系 链的概念 表的概念 表链关系 规则的概念 查询规则 添加规则 删除iptables中的记录 修改规则 更详细的命令(5链4表) 防火墙基本概念 什么是防火墙? 在…...
)
安全管理中心(设备和技术注解)
网络安全等级保护相关标准参考《GB/T 22239-2019 网络安全等级保护基本要求》和《GB/T 28448-2019 网络安全等级保护测评要求》 密码应用安全性相关标准参考《GB/T 39786-2021 信息系统密码应用基本要求》和《GM/T 0115-2021 信息系统密码应用测评要求》 1系统管理 1.1对系统管…...
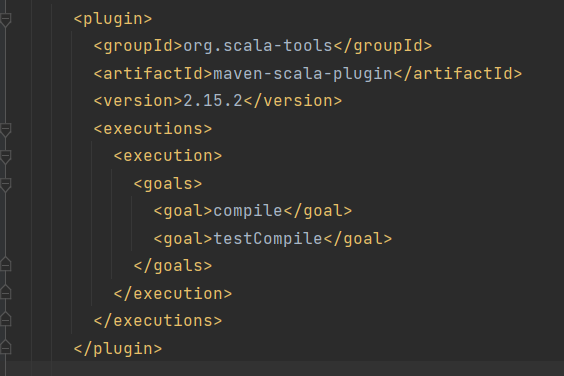
Failed to execute org.scala-tools:maven-scala-plugin:2.15.2解决
原因也不是很清楚,查看一个博主文章(net.alchim31.maven:scala-maven-plugin:maven依赖无法下载或无法编译)得到的解决方案: 在idea的terminal执行以下语句即可实现maven对scala代码的编译: mvn clean scala:compile compile pac…...

C#中委托和事件的使用总结
委托(delegate)特别用于实现事件和回调方法。所有的委托(Delegate)都派生自 System.Delegate 类。事件是一种特殊的多播委托,仅可以从声明事件的类或结构中对其进行调用。类或对象可以通过事件向其他类或对象通知发生的…...

基于STM32的外部中断(EXTI)在嵌入式系统中的应用
外部中断(External Interrupt,EXTI)是STM32嵌入式系统中常见且重要的功能之一。它允许外部事件(例如按键按下、传感器触发等)通过适当的引脚触发中断,从而应用于各种嵌入式系统中。在STM32微控制器中&#…...
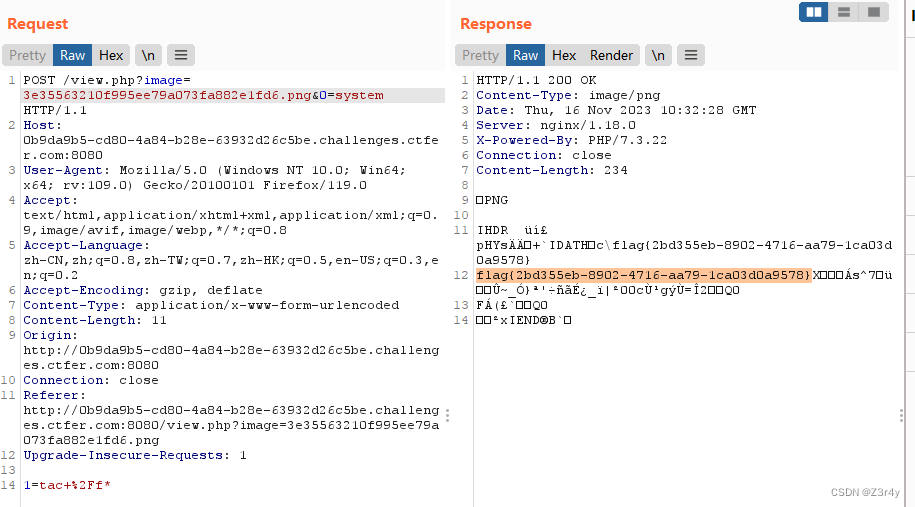
【心得】PHP的文件上传个人笔记
目录 1 php的文件上传绕过 黑名单绕过 2 php文件上传的00截断 3 iconv字符转换异常后造成了字符截断 4 文件后缀是白名单的时候的绕过 web服务器的解析漏洞绕过 5.高级文件上传绕过 1 .htaccess nginx.htaccess 2 服务端内容检测 3 配合伪协议来绕过 4.配合日志包含绕…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
