二项分布和泊松分布
一、二项分布
1.1 n重伯努利试验
若是二项分布,则必是n重伯努利试验概型。即:每次试验只有两种结果
与
,且在每次试验中A发生的概率相等,即P(A)=p,将这种试验独立重复n次,则称这种试验为n重伯努利试验,也叫n重伯努利概率模型,所以二项分布也叫伯努利分布。
1.2 什么是二项
二项是指:把一个随机试验的结果只划分成两种。例如:要么A事件发生,要么A事件没发生,记为:
和
;所以二项的涵义可理解为:随机变量X的取值只有两个,第一个取值的代表某事件发生了,第二个则代表某事件未发生。再例如:将考试成绩的结果分为两类,第一类是成绩≥60分,则第二类是成绩<60分。
1.2 二项分布X~B
用随机变量X来表示在n重伯努利试验中A事件发生的次数,其概率函数为:
,
,
则称:X服从参数为(n,p)的二项分布,记作X~B。期望:E(X)=np;方差:D(X)=n·p(1-p)。
1.4 二项分布的性质
一般地,对于固定的n及p,当k增加时,概率P(X=k)先是随之增加直至到达最大值,随后单调减少:① 当(n+1)p为整数时,概率P(X=k)在k=
=p(n+1)和(n+1)p-1时达到最大值;② 不为整数时,概率P(X=k)在k=
在p(n+1)时达到最大值。称
为二项分布的最可能值。说人话就是:当发生k次为几时,二项分布的概率值最大,最大即意味着最有可能发生。
1.5 二项分布示例
抛一枚硬币,设朝上的结果为随机变量X。问:假设一共抛5次,正面和反面发生的概率均为1/2,求3次正面朝上的概率:
,答:5次中发生3次正面朝上的概率为31.25%
随机变量X(正面朝上次数)的期望:E(X)=np=(
),指:抛5次,正面朝上次数的平均结果是2.5次。
随机变量X(正面朝上次数)的方差:D(X)=n·p(1-p)=(
,指:抛5次,正面朝上出现次数的方差为1.2。
二、泊松分布
2.1 与二项分布的区别
泊松分布可以理解为:二项分布的试验次数趋向于无穷大时,事件A发生的次数及概率的分布。在理论上,泊松分布是二项分布的极限分布。当趋于无限次数时,可理解为一个时段或时空内,将每次试验是在分割成每秒/每分等事件单位下的事件A是否发生。如下图所示。
重点:一般地,当n较大,p较小,np大小适当时,以(n,p)为参数的二项分布可近似看成参数为
的泊松分布,这样可利用泊松分布对二项分布作近似计算,实际计算时,
时近似的效果极好。
2.2 泊松分布的涵义
泊松分布是用来描述:在一个比较长的时间段(时空)里面,一个很小概率事件发生的次数。例如:一段时间内电话总台收到的来电呼叫次数;一段时间内,账户登录系统发生故障的次数;在一天内,来到商场的顾客人数;游泳池里一平方米内,从水底冒出来泡的次数等。
2.3 泊松分布X~P
用随机变量X来表示在在一段时间或时空内A事件发生的次数,其概率函数为:
,
其中
,称X服从参数为
的泊松分布(poisson distribution),记作X~P(
)。
其中期望E(X)和方差D(X)都为:
。
2.4 泊松分布查表得概率
例如:k=5次,
=7,依下表查的P(X=5)=0.369≈37%;
例如:k≤3次,
=4,依下表查的P(X≤3)=0.0183+0.0916+0.2381+0.4335=0.7815≈78%。
相关文章:

二项分布和泊松分布
一、二项分布 1.1 n重伯努利试验 若是二项分布,则必是n重伯努利试验概型。即:每次试验只有两种结果 与 ,且在每次试验中A发生的概率相等,即P(A)p,将这种试验独立重复n次,则称这种试验为n重伯努利试验&#…...

【飞控调试】DJIF450机架+Pixhawk6c mini+v1.13.3固件+好盈Platinium 40A电调无人机调试
1 背景 由于使用了一种新的航电设备组合,在调试无人机起飞的时候遇到了之前没有遇到的问题。之前用的飞控(Pixhawk 6c)和电调(Hobbywing X-Rotor 40A),在QGC里按默认参数配置来基本就能平稳飞行࿰…...
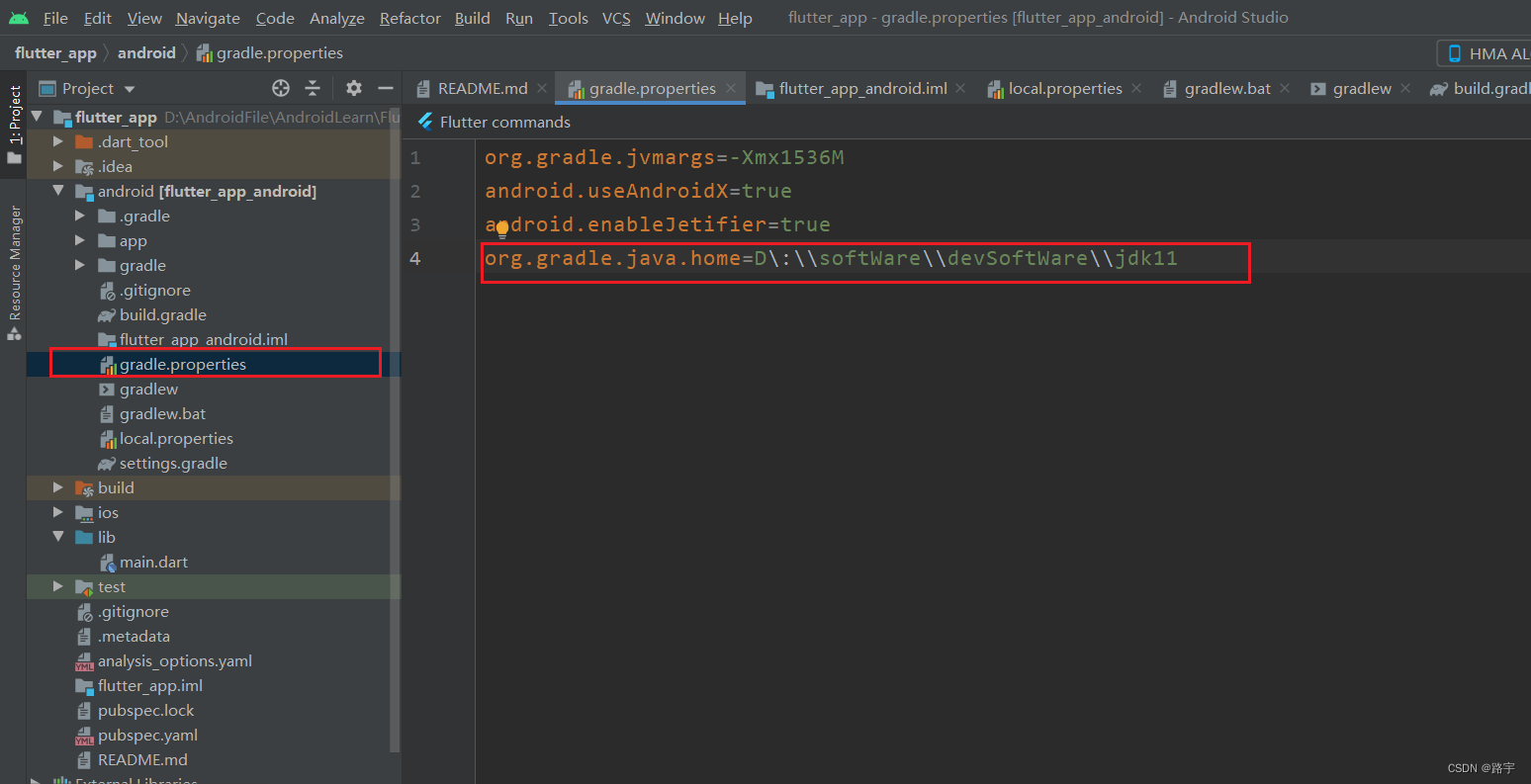
Android studio配置Flutter开发环境报错问题解决
博主前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住也分享一下给大家 👉点击跳转到教程 报错问题截图 报错原因已经给出: You need Java 11 or higher to build your app with this version of G…...

2023.11.18 -自用hadoop高可用环境搭建命令
启动hadoop高可用环境 # 1.先恢复快照到高可用环境 # 2.三台服务器启动zookeeper服务 [rootnode1 ~]# zkServer.sh start [rootnode2 ~]# zkServer.sh start [rootnode3 ~]# zkServer.sh start 查看服务状态: [rootnode]# zkServer.sh status 关闭zk服务的命令是: [rootnode]# …...

【Linux】常用系统工作命令
一、Linux文档目录结构 在Linux系统中,目录、字符设备、套接字、硬盘、光驱、打印机等都被抽象成文件形式,“Linux系统中一切都是文件”。Linux系统中的一切文件都是从"根"目录(/)开始的,并按照文件系统层次…...

深入理解网络协议:通信世界的基石
💂 个人网站:【 海拥】【神级代码资源网站】【办公神器】🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交流的小伙伴,请点击【全栈技术交流群】 在当今数字化时代,网络协议是连接世…...
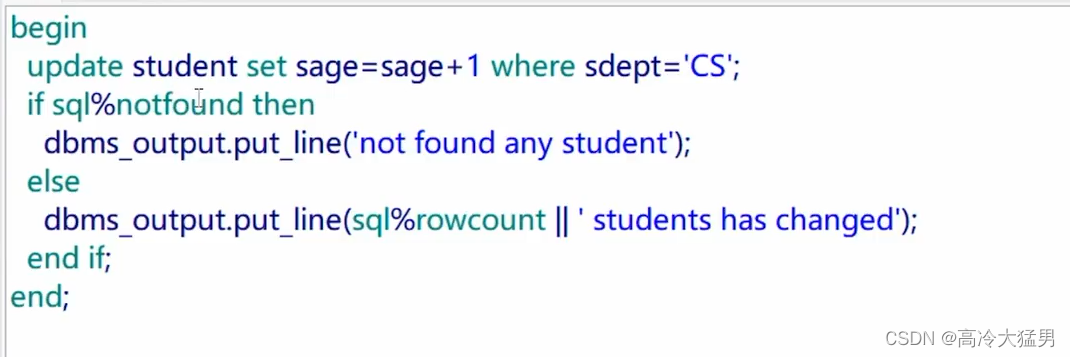
PL/SQL编程
一、Oracle常用函数 concat:用于连接两个字符串。 CONCAT(Oraok, .com) -- Result: Oraok.com ceil:小数点向上取整。 secect ceil(7.3) from dual --Result: 8 dual表是oracle系统为计算设计的一张临时表 select sysdate as 系统日期 from dual…...

Prompt提示词——什么是CRISPE框架?QCIPSPE框架?
框架介绍 【CRISPE】框架 是由 Matt Nigh 提出并发布的提示词书写框架,共由五部分组成。 这个框架(CRISPE)主要包括五个部分,用于指导用户向ChatGPT提问。首先,通过设定ChatGPT的角色(Capacity and Role&…...

Nginx的核心配置文件
Nginx的核心配置文件 学习Nginx首先需要对它的核心配置文件有一定的认识,这个文件位于Nginx的安装目录/usr/local/nginx/conf目录下,名字为nginx.conf 详细配置,可以参考resources目录下的<<nginx配置中文详解.conf>> Nginx的核…...
)
Java,集合框架,关于Collection接口(子接口List和Set)
目录 数组储存多个数据方面的特点: Java集合框架体系:(Java.util包下) Collection接口中的方法测试: 迭代器(Iterator)的作用:用来遍历集合元素。 增强for循环(即for…...

已安装的nginx追加ssl模块
Nginx开启SSL模块1 切换到源码包: cd /usr/local/src/nginx-1.11.3 2 查看nginx原有的模块 /usr/local/nginx/sbin/nginx -V 在configure arguments:后面显示的原有的configure参数如下: –prefix/usr/local/nginx --with-http_stub_status_module …...

大语言模型|人工智能领域中备受关注的技术
个人主页:【😊个人主页】 系列专栏:【❤️其他领域】 文章目录 前言关于大语言模型大语言模型是什么?大语言模型有什么用?文案写作知识库回答文本分类代码生成 AWS 如何通过 LLM 提供帮助?Amazon BedrockAmazon SageM…...
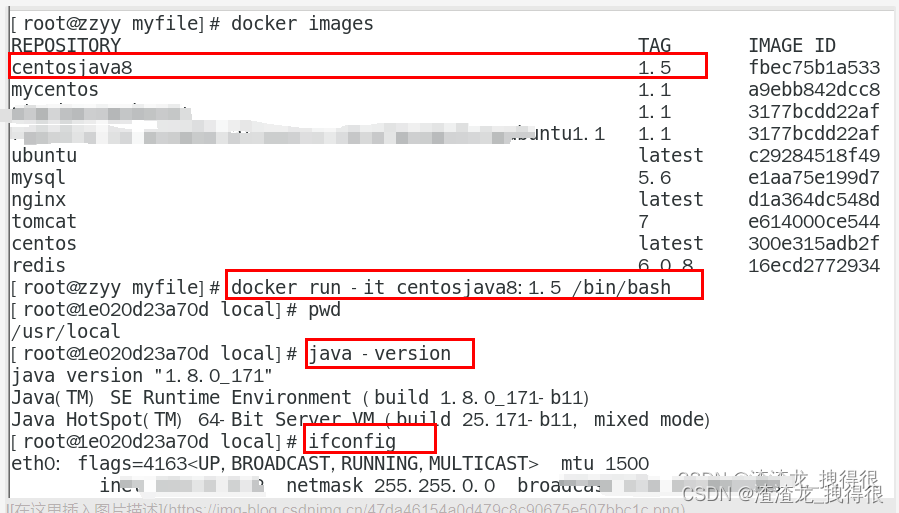
Docker之DockerFile解析
DockerFile解析 是什么 Dockerfile是用来构建Docker镜像的文本文件,是由一条条构建镜像所需的指令和参数构成的脚本。 概述 官网 https://docs.docker.com/engine/reference/builder/ 构建三步骤 编写Dockerfile文件 docker build命令构建镜像 docker run依镜像运…...
NSSCTF第13页(2)
[HNCTF 2022 Week1]Challenge__rce 提示?hint 访问看到了源码 <?php error_reporting(0); if (isset($_GET[hint])) { highlight_file(__FILE__); } if (isset($_POST[rce])) { $rce $_POST[rce]; if (strlen($rce) < 120) { if (is_string($rce…...

基于吉萨金字塔建造算法优化概率神经网络PNN的分类预测 - 附代码
基于吉萨金字塔建造算法优化概率神经网络PNN的分类预测 - 附代码 文章目录 基于吉萨金字塔建造算法优化概率神经网络PNN的分类预测 - 附代码1.PNN网络概述2.变压器故障诊街系统相关背景2.1 模型建立 3.基于吉萨金字塔建造优化的PNN网络5.测试结果6.参考文献7.Matlab代码 摘要&a…...
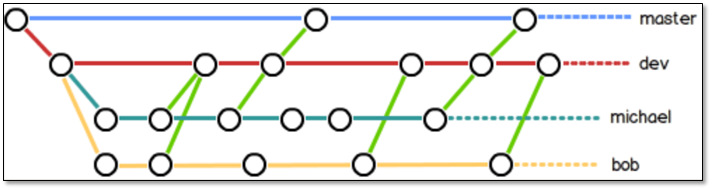
Git详解及 github使用
1.1 关于版本控制 开始之前先看一个没有版本控制的例子 1.1.1 本地版本控制 本地版本控制系统 许多人习惯用复制整个项目目录的方式来保存不同的版本,或许还会改名加上备份时间以示区别。这么做唯一的 好处就是简单,但是特别容易犯错。有时候会混淆所在…...
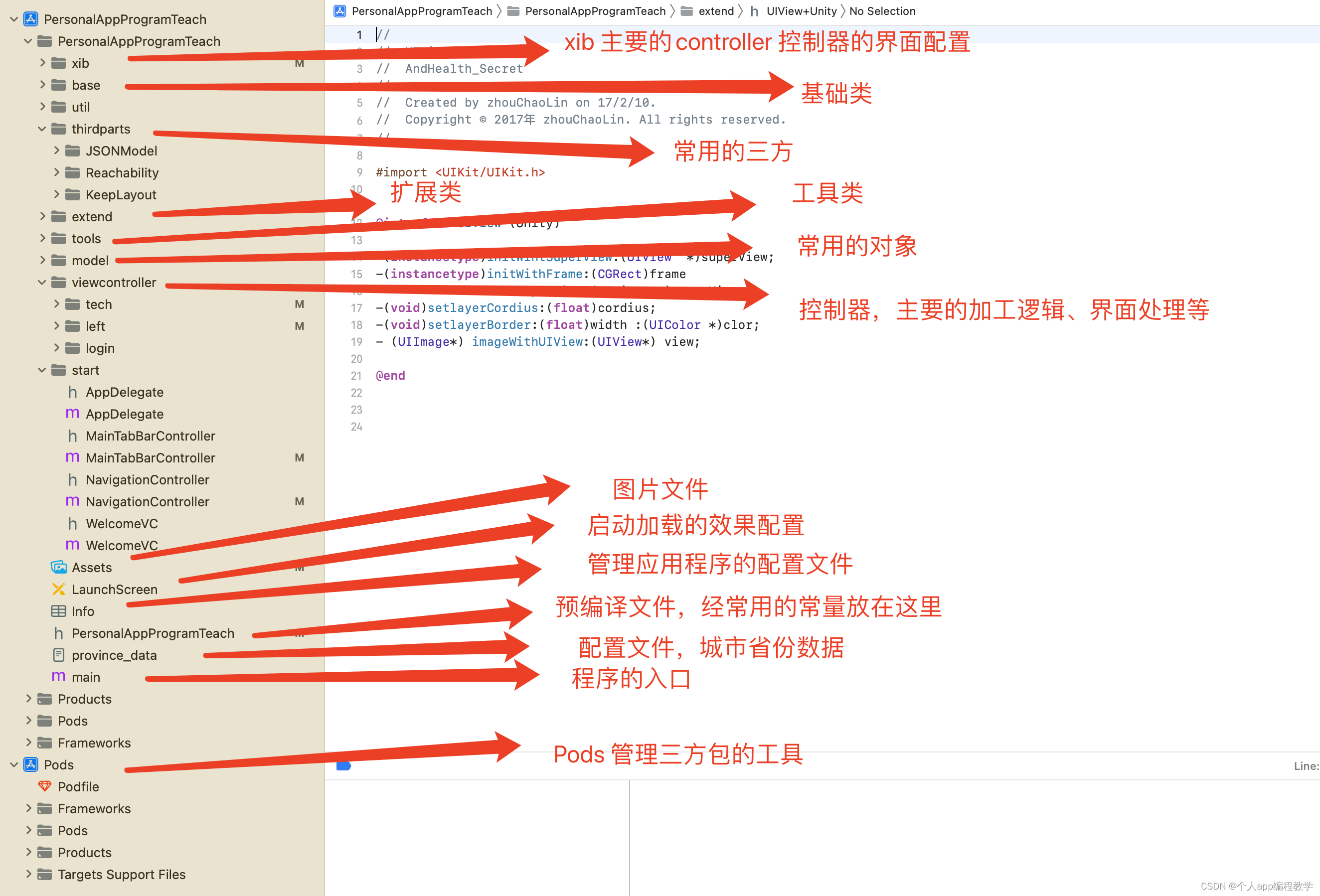
iOS源码-工程目录讲解
1、 工程目录 1.1、xib 主要的界面渲染控制,ios开发常用的界面,可以在这里快速开发出来 1.2、base 基本的类,子类继承base类,就具备父类的方法,无需在重写 1.3、util 基础的类一些,处理时间等 1.4、…...
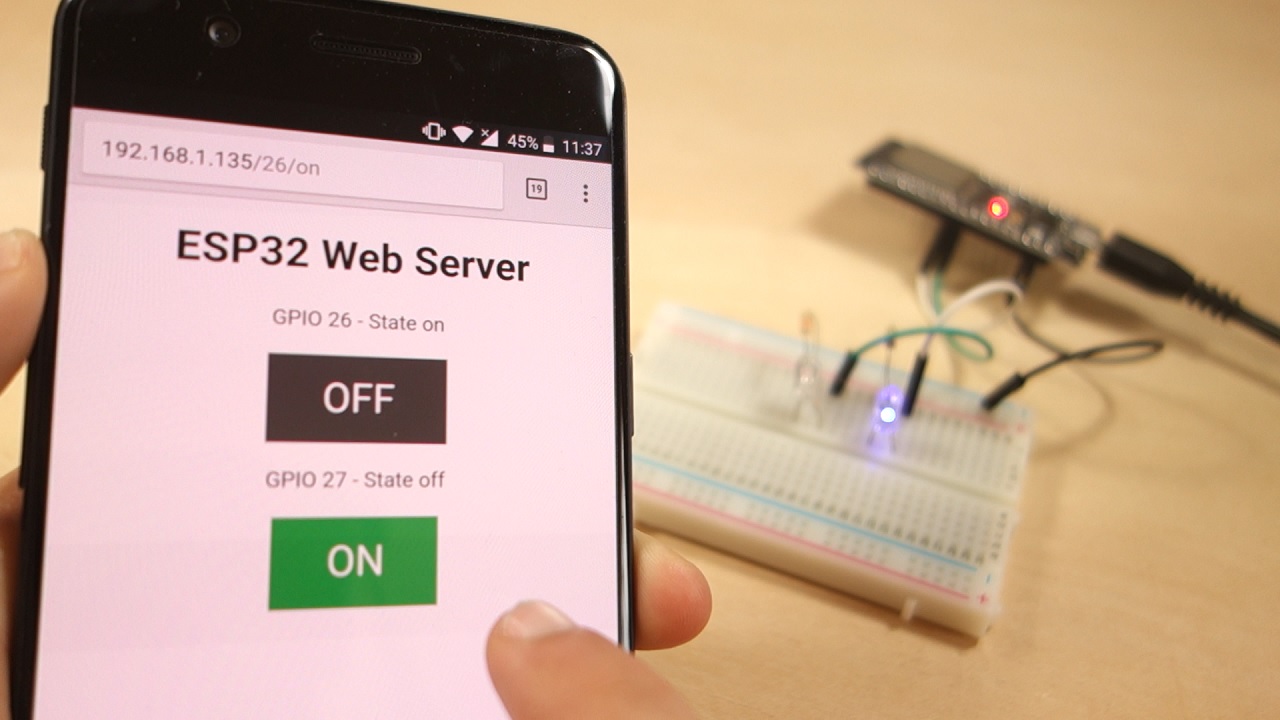
ESP32 Arduino实战协议篇-搭建独立的 Web 服务器
在此项目中,您将创建一个带有 ESP32 的独立 Web 服务器,该服务器使用 Arduino IDE 编程环境控制输出(两个 LED)。Web 服务器是移动响应的,可以使用本地网络上的任何浏览器设备进行访问。我们将向您展示如何创建 Web 服务器以及代码如何逐步工作。 项目概况 在直接进入项目…...

多维时序 | MATLAB实现PSO-BiLSTM-Attention粒子群优化双向长短期记忆神经网络融合注意力机制的多变量时间序列预测
多维时序 | MATLAB实现PSO-BiLSTM-Attention粒子群优化双向长短期记忆神经网络融合注意力机制的多变量时间序列预测 目录 多维时序 | MATLAB实现PSO-BiLSTM-Attention粒子群优化双向长短期记忆神经网络融合注意力机制的多变量时间序列预测预测效果基本介绍模型描述程序设计参考…...
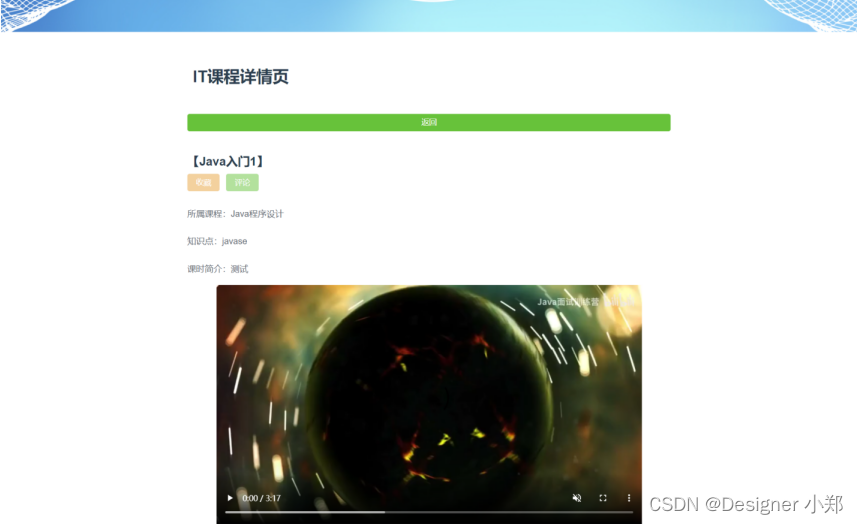
【开源】基于Vue.js的在线课程教学系统的设计和实现
项目编号: S 014 ,文末获取源码。 \color{red}{项目编号:S014,文末获取源码。} 项目编号:S014,文末获取源码。 目录 一、摘要1.1 系统介绍1.2 项目录屏 二、研究内容2.1 课程类型管理模块2.2 课程管理模块2…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
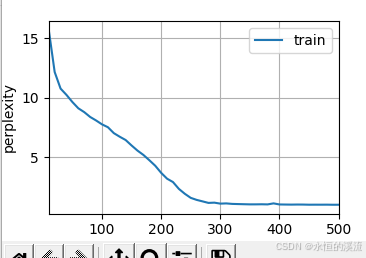
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...
