iOS源码-工程目录讲解
1、 工程目录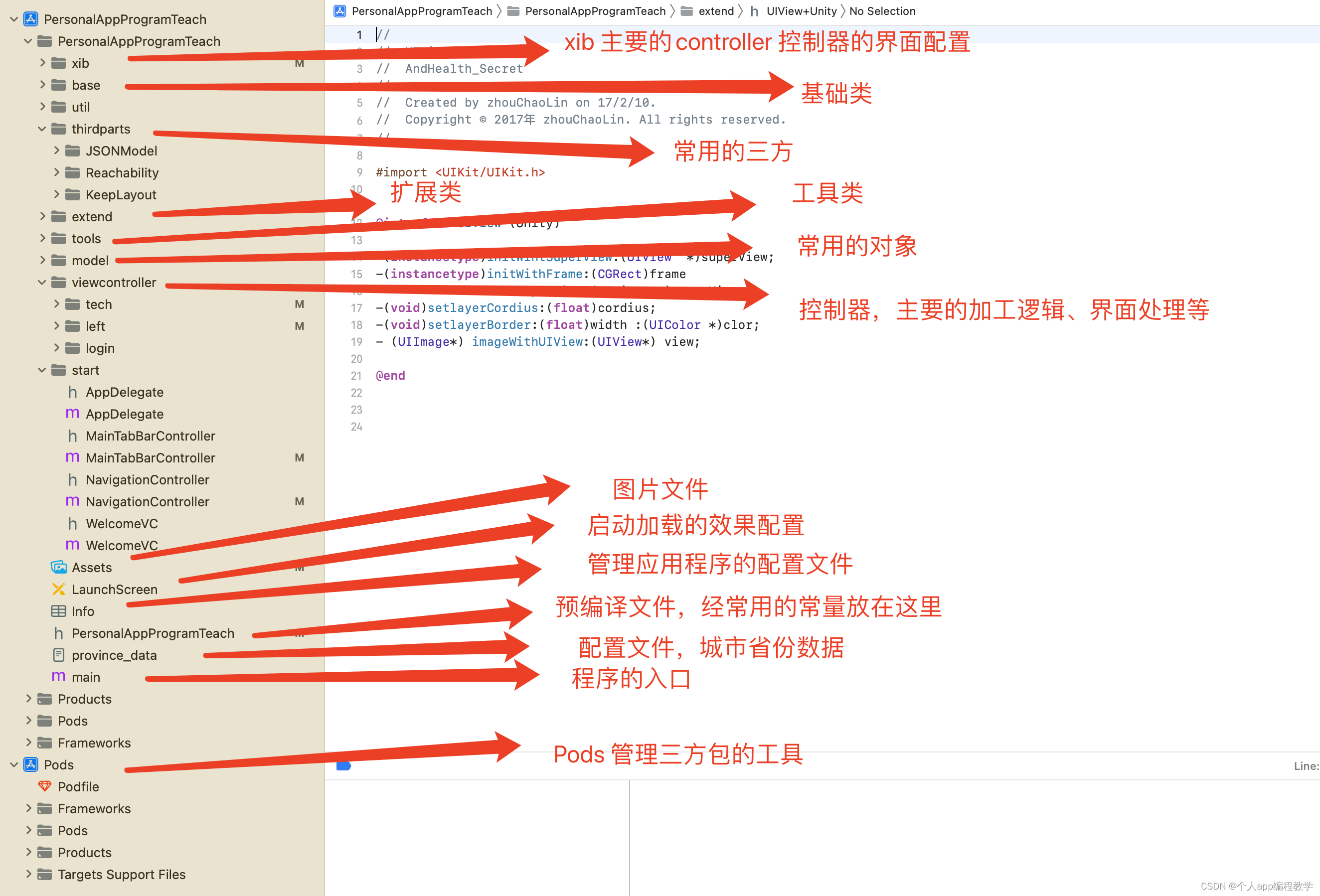
1.1、xib
主要的界面渲染控制,ios开发常用的界面,可以在这里快速开发出来
1.2、base
基本的类,子类继承base类,就具备父类的方法,无需在重写
1.3、util
基础的类一些,处理时间等
1.4、thirdParts 常用的三方
如 jsonModel 反序列化解析的三方类,将String 处理成对象
1.5、扩展类
类扩展,可以定义一个类的多个扩展,当前类就具备扩展的所有方法
1.6、工具类
一些常用的类,用于处理逻辑用
1.7、对象
数据的承载对象
1.8、ViewController
控制器,用来处理界面的逻辑
1.9、Assets
图片文件管理,加载界面的图片
1.10、Assets
图片文件管理,加载界面的图片
1.11、LaunchScreen.storyboard
工程启动的界面配置
1.12、LaunchScreen.storyboard
1.13、Info.plist
配置文件,常用的权限管理等
1.14、PersonalAppProgramTeach.pch
预编译文件
相关文章:

iOS源码-工程目录讲解
1、 工程目录 1.1、xib 主要的界面渲染控制,ios开发常用的界面,可以在这里快速开发出来 1.2、base 基本的类,子类继承base类,就具备父类的方法,无需在重写 1.3、util 基础的类一些,处理时间等 1.4、…...
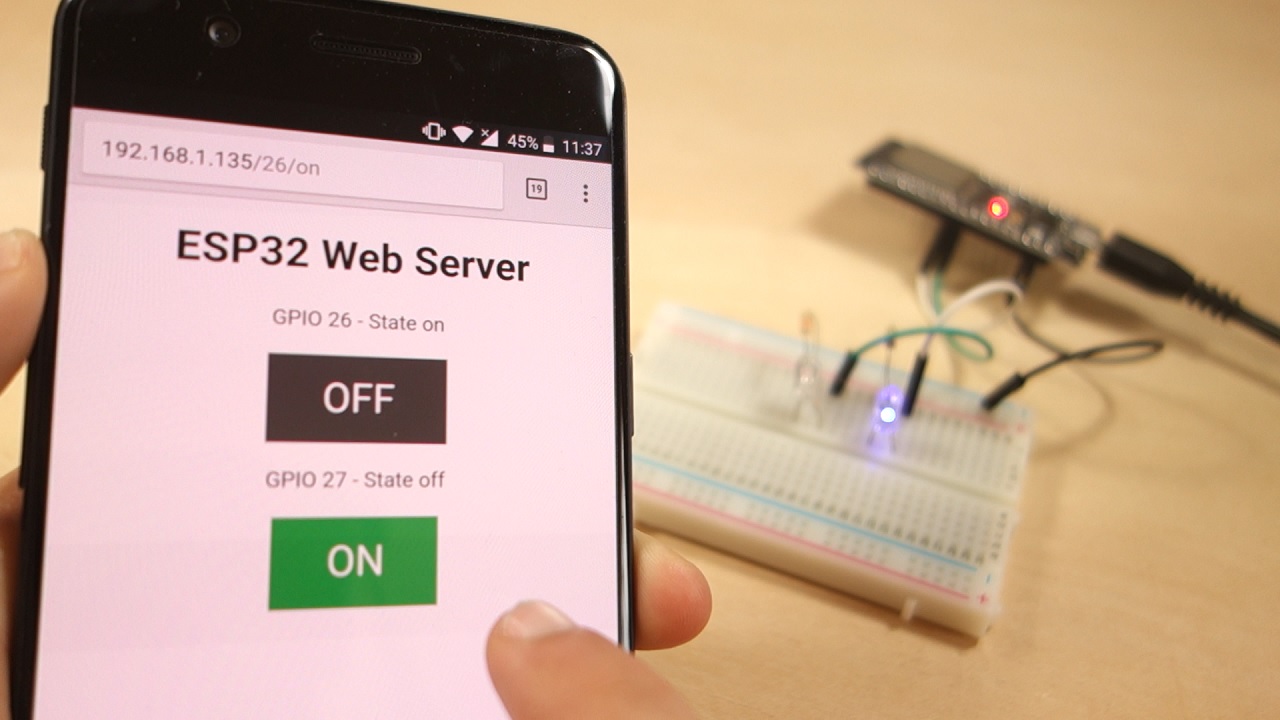
ESP32 Arduino实战协议篇-搭建独立的 Web 服务器
在此项目中,您将创建一个带有 ESP32 的独立 Web 服务器,该服务器使用 Arduino IDE 编程环境控制输出(两个 LED)。Web 服务器是移动响应的,可以使用本地网络上的任何浏览器设备进行访问。我们将向您展示如何创建 Web 服务器以及代码如何逐步工作。 项目概况 在直接进入项目…...

多维时序 | MATLAB实现PSO-BiLSTM-Attention粒子群优化双向长短期记忆神经网络融合注意力机制的多变量时间序列预测
多维时序 | MATLAB实现PSO-BiLSTM-Attention粒子群优化双向长短期记忆神经网络融合注意力机制的多变量时间序列预测 目录 多维时序 | MATLAB实现PSO-BiLSTM-Attention粒子群优化双向长短期记忆神经网络融合注意力机制的多变量时间序列预测预测效果基本介绍模型描述程序设计参考…...
【开源】基于Vue.js的在线课程教学系统的设计和实现
项目编号: S 014 ,文末获取源码。 \color{red}{项目编号:S014,文末获取源码。} 项目编号:S014,文末获取源码。 目录 一、摘要1.1 系统介绍1.2 项目录屏 二、研究内容2.1 课程类型管理模块2.2 课程管理模块2…...

CentOS 安装etcd集群 —— 筑梦之路
环境说明 192.168.1.11 192.168.1.12 192.168.1.13 yum在线安装 yum install etcd -y #etcd01 cat > /etc/etcd/etcd.conf <<EOF ETCD_NAMEetcd01 ETCD_LISTEN_PEER_URLS"http://0.0.0.0:2380" ETCD_LISTEN_CLIENT_URLS"http://0.0.0.0:2379&quo…...
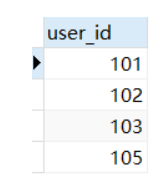
mysql 实现去重
个人网站 首发于公众号小肖学数据分析 1、试题描述 数据表user_test如下,请你查询所有投递用户user_id并且进行去重展示,查询结果和返回顺序如下 查询结果和返回顺序如下所示 解题思路: (1) 对user_id列直接去重: ÿ…...

类模板成员函数类外实现
#include<iostream> #include<string> using namespace std;//类模板成员函数类外实现 template<class T1,class T2> class Person { public:Person(T1 name,T2 age); // { // this->m_namename; // this->m_ageage; // }void showPerson(); // { /…...
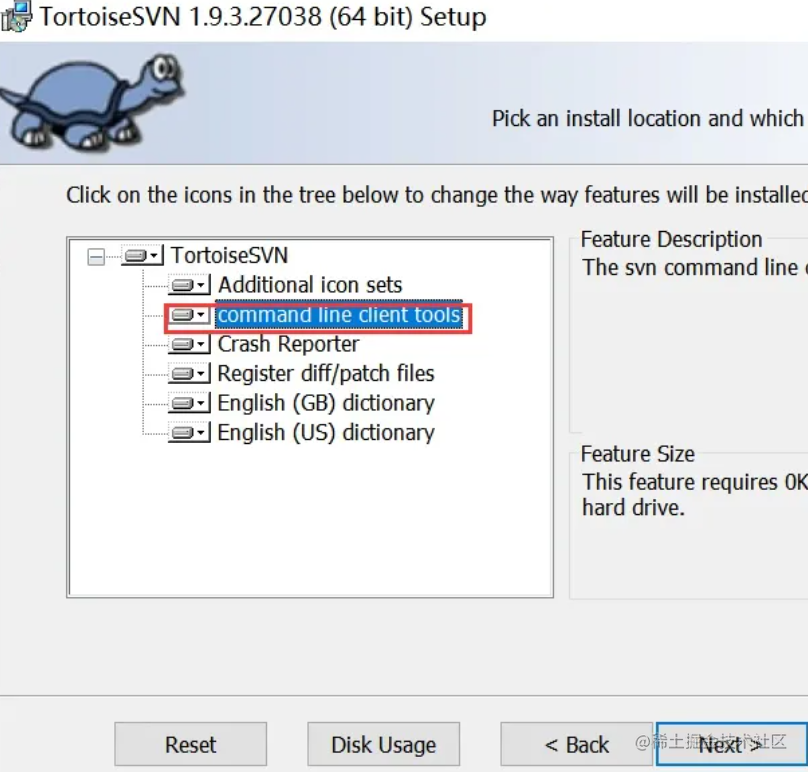
多svn仓库一键更新脚本分享
之前分享过多git仓库一键更新脚本,本期就分享下svn仓库的一键更新脚本 1、首先需要设置svn为可执行命令行 打开SVN安装程序,选择modify,然后点击 command client tools,安装命令行工具 2、update脚本 echo 开始更新SVN目录&…...
)
C语言程序设计(入门)
考虑到期末临近,大一的学生该考c语言程序设计了吧,整一小篇给爱摆烂的小萌新复习一下降低挂科的风险 1. 1.1 main 函数 int main() {// 程序的入口,执行从这里开始return 0; // 表示程序正常结束 }1.2 语句和分号 C语言中的语句以分号结束…...
短视频账号矩阵系统源码
短视频账号矩阵系统源码搭建步骤包括以下几个方面: 1. 确定账号类型和目标受众:确定要运营的短视频账号类型,如搞笑、美食、美妆等,并明确目标受众和定位。 2. 准备账号资料:准备相关资质和资料,如营业执照…...
基于SSM的在线投稿系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...
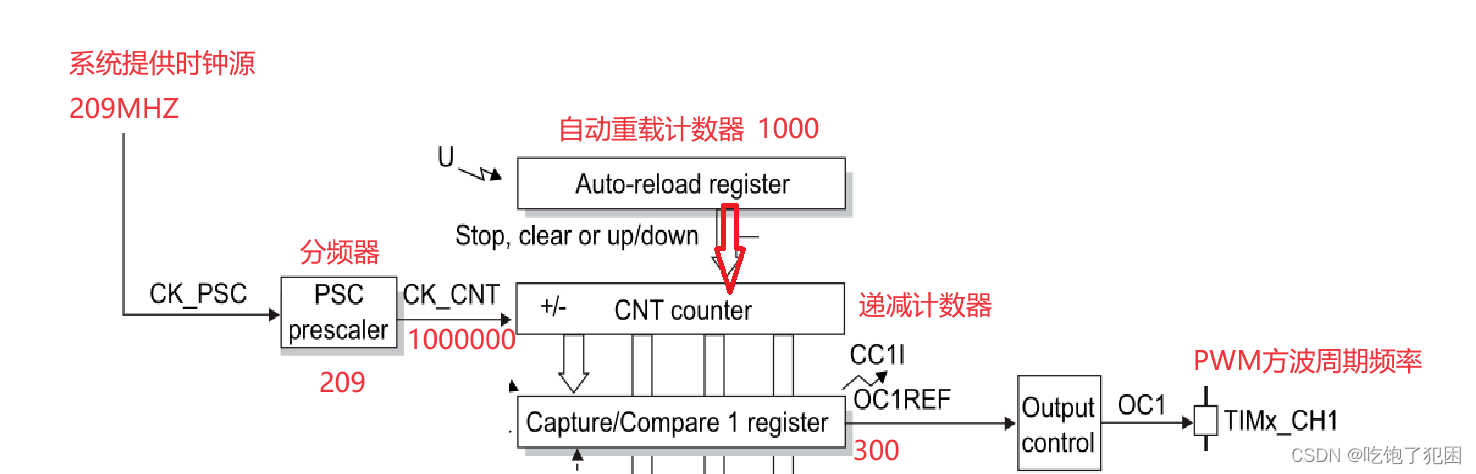
PWM实验
PWM相关概念 PWM:脉冲宽度调制定时器 脉冲:方波信号,高低电平变化产生方波 周期:高低电平变化所需要时间 频率:1s钟可以产生方波个数 占空比:在一个方波内,高电平占用的百分比 宽度调制:占…...
Python武器库开发-flask篇之session与cookie(二十六)
flask篇之session与cookie(二十六) 在 Flask 中,可以使用 session 来在不同请求之间存储和传递数据。Session 在客户端和服务器端之间交换,但是数据存储在服务器端。 Session 与 Cookie 的区别 session 和 cookie 都可以用来在不同请求之间存储和传递…...

深度学习YOLO安检管制物品识别与检测 - python opencv 计算机竞赛
文章目录 0 前言1 课题背景2 实现效果3 卷积神经网络4 Yolov55 模型训练6 实现效果7 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习YOLO安检管制误判识别与检测 ** 该项目较为新颖,适合作为竞赛课题方向&…...

vite+react+typescript 遇到的问题
1.找不到模块“vite”。你的意思是要将 “moduleResolution” 选项设置为 “node”,还是要将别名添加到 “paths” 选项中 tsconfig.json 中 compilerOptions:{“moduleResolution”: node} 2.未知的编译器选项“allowImportingTsExtensions” 该选项用于控制是否…...
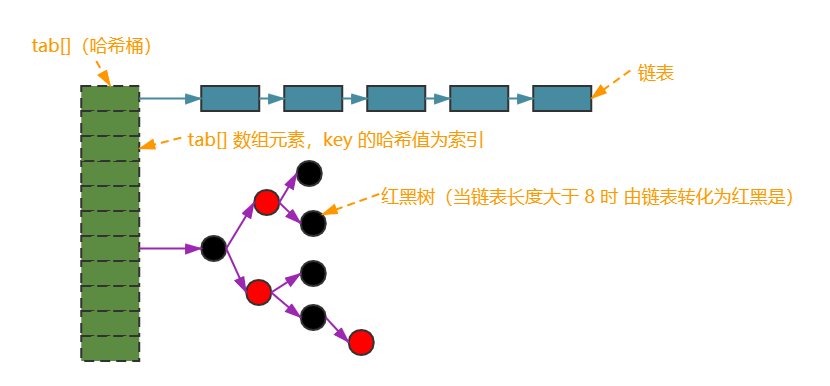
数据结构及八种常用数据结构简介
data-structure 数据结构是一种存在某种关系的元素的集合。“数据” 是指元素;“结构” 是指元素之间存在的关系,分为 “逻辑结构” 和 “物理结构(又称存储结构)”。 常用的数据结构有 数组(array)、栈&…...
)
阿里云配置ssl(Apache)
阿里云申请证书,有个专门的免费的申请方式与普通证书是平级的功能; 访问服务器,判断apache是不是开启ssl功能,如果没有安装就安装它 [rootcentos ~]# rpm -qa | grep mod_ssl //什么没显示说明没装 yum install mod_ssl openssl …...

阿里云linux升级新版本npm、nodejs
在阿里云服务器上编译部署NextJS工程发现 alibaba linux默认yum install npm安装的版本太低, 使用以下方式升级node、npm新版本。 1、卸载现有版本 yum remove nodejs npm -y2、安装新版本 sudo yum install https://rpm.nodesource.com/pub_21.x/nodistro/repo/nodesource-…...

如何在el-tree懒加载并且包含下级的情况下进行数据回显-02
上一篇文章如何在el-tree懒加载并且包含下级的情况下进行数据回显-01对于el-tree懒加载,包含下级的情况下,对于回显提出两种方案,第一种方案有一些难题无法解决,我们重点来说说第二种方案。 第二种方案是使用这个变量对其是否全选…...

Pytorch 网络冻结的三种方法区别:detach、requires_grad、with_no_grad
1、requires_grad requires_gradTrue # 要求计算梯度; requires_gradFalse # 不要求计算梯度;在pytorch中,tensor有一个 requires_grad参数,如果设置为True,那么它会追踪对于该张量的所有操作。在完成计算时可以通过调…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
