漫谈广告机制设计 | 万剑归宗:聊聊广告机制设计与收入提升的秘密(3)
书接上文漫谈广告机制设计 | 万剑归宗:聊聊广告机制设计与收入提升的秘密(2),我们聊到囚徒困境是完全信息静态博弈,参与人存在占优策略,最终达到占优均衡,并且是对称占优均衡。接下来我们继续举例子说明一些博弈论的概念,并向读者们灌输一个思想:做机制设计要分析各方利益得失,要指哪打哪,而不是毫无目的地探索尝试。
(一)
下面这个例子叫智猪博弈。
假设猪圈里有一头大猪、一头小猪,都是聪明的猪。猪圈的一头有猪食槽,另一头安装着控制猪食供应的按钮,按一下按钮会有10个单位的猪食进槽,但是谁按按钮就会首先付出2个单位的成本。按钮和猪食槽在相反位置,按按钮的猪要付出2个单位的成本,并且丧失了先到槽边进食的机会。若小猪先到槽边进食,因为缺乏竞争,进食的速度一般,最终大小猪吃到食物的比率是6∶4;若大猪先到槽边进食,大猪会霸占剩余所有猪食,最终大小猪收益比9∶1;若同时到槽边进食,大猪进食速度加快,最终大小猪收益比是7∶3。
用博弈论中的报酬矩阵可以更清晰地刻画出大猪和小猪的选择情况。如当大猪和小猪都选择行动时,各自都会付出2个单位的成本,获得的收益是7:3,最终的效用是5:1。下面我们分析一下大猪和小猪是否有最优的策略。

对于大猪而言,如果小猪行动,那么大猪行动的效用是5,等待的效用是9,那么大猪的最优策略是等待;如果小猪等待,那么大猪行动的效用是4,等待的效用是0,那么大猪的最优策略是行动。也就是说大猪的最优策略依赖小猪的策略。
对于小猪而言,如果大猪行动,那么小猪行动的效用是1,等待的效用是4,那么小猪的最优策略是等待;如果大猪等待,那么小猪行动的效用是-1,等待的效用是0,那么小猪的最优策略还是等待。也就是说无论大猪做什么策略,小猪的最优策略都是等待,在这种情况下,大猪不得不选择行动,最后大猪的效用是4,小猪的效用也是4,小猪"搭了便车"。
这样的例子可以用来解释现实生活中为什么能者必须多劳的问题,比如为什么市场的先行者获得效用可能还不如后来者,职场中有能力的人不一定获得比平庸者更高的效用,花钱投放广告的人最终可能是替竞对做了宣传。
这个博弈最终也会达到均衡状态,即大猪行动,小猪等待,这个均衡称之为重复剔除的占优策略均衡。这个均衡相比占优均衡变弱了一些。
(二)
接下来说明一下纳什均衡(约翰·纳什于获得1994年诺贝尔经济学奖)。

一个博弈有两个参与人,他们的策略和收益情况用以下收益矩阵表示。
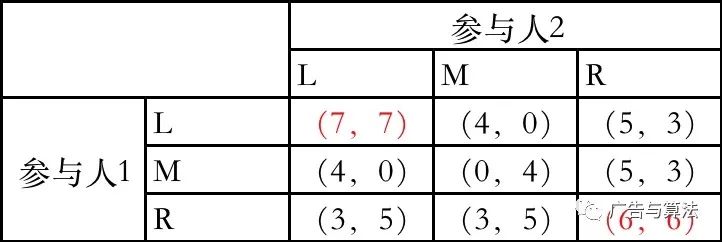
图中参与人1执行L策略,参与人2执行L策略,或者参与人1执行R策略,参与人2执行R策略均称之为纳什均衡,即当所有参与人持对应策略后,任一参与人均无诱因偏离这一均衡。可以看出纳什均衡不唯一。可见纳什均衡相比占优均衡要更弱一些。
然后我们举个猜拳的例子,石头剪刀布,其收益矩阵如下:
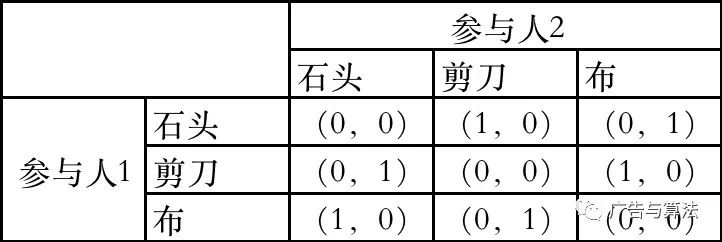
分析收益矩阵会发现,这个博弈连上面说的纳什均衡都没有。我们把策略从纯策略扩展到混合策略,纯策略是指以100%的概率执行某个策略,混合策略是以不同的概率执行不同的策略,整体概率为100%。那在猜拳游戏中,参与人的最优混合策略可以计算出来,就是随机出石头、剪刀、布,三个策略的概率分别是1/3,1/3,1/3,这也是符合基础认知的。这个平衡状态称之为混合策略纳什均衡。

好了,关于博弈论的例子我们就举到这里。读者们需要理解几个概念:不完全信息静态博弈、占优均衡<重复剔除占优均衡<纯策略纳什均衡<混合策略纳什均衡(<的含义是包含于的意思)。在每个有限策略式博弈(参与人和战略数据均有限)都存在纳什均衡,但有可能是混合战略纳什均衡。
拍卖属于博弈论的范畴,因此分析拍卖者在这场博弈中的利益情况,并基于利益情况设置想要的机制是十分重要的。特别地,当机制的参数或者机制本身变动时,或者广告模型或者排序策略更新都需要考虑一下广告主的反应的,而这种反应可能是长期的,AB试验看不出来的,甚至无法自证的,这也造成了目前的广告机制设计要么返祖到运筹优化,要么进化到深度学习模型,前几年微软亚研院的刘铁岩老师提出的算法博弈论的概念也逐渐势微,各种模型引入历史出价和分配结果的情况大行其道。
机制设计者追求的机制是参与各方能够真实报出内心的价值,这样机制设计者才能把有限的资源分配给最能创造价值的人手里,达到社会效率最大化。当然,这个理想十分美好。
(三)
言归正传,我们介绍拍卖的知识。
印象中的拍卖是一个拍卖师,对台下的买主喊着『十万一次,十万两次,十万三次』,然后以『成交』作为拍卖的结束,商品以十万卖出,可以发现拍卖是一种价格发现机制,这种机制在一系列明确的规则下,由投标人的报价确定某种资源的配置并形成最终的交易价格。也就是说通过竞价,将潜在的买主意愿支付的信息引导出来,拍卖品的分配和需要支付的价格均基于买主的报价。拍卖包含两个必要的要素:确定配置资源与支付价格的规则和买者的报价。拍卖应该与人们的商品交易活动同时出现,是一种十分古老的交易形式,那时候可能也有叫价举牌。拍卖也有着不光彩的历史,有文字记载的拍卖是古巴比伦时期的拍卖『新娘』,但就拍卖本身与而言,与现在的拍卖没有多大区别。中国最早有文字记载的拍卖活动在唐朝。后来拍卖不断延伸到商品交易的各个领域,拍卖和固定价格(非买主报价)相结合构成了经济生活的方方面面。
从不完全信息博弈的角度看拍卖,拍卖是出售者与竞买者的博弈,这种博弈的形式是丰富多彩的,可以从下图看出各式各样的拍卖。引用戎文晋 老师的《关键词拍卖与理论实践》。

从前面的图中看出,拍卖的应用形式是千变万化,丰富多彩的,但是人们总想从复杂的形式中抽象出基本形式,万变不离其宗,抓住本质就好分析问题了。不同拍卖形式之间的本质差别是在于资源的分配规则、支付规则和报价方式。1980年Engelbrecht-Wiggans 提出了这样分类方法,将拍卖分为以下四种:
1)公开增价拍卖(英式拍卖):这就是最常见的拍卖了,竞买者公开报价加价,直到没有人加价为止,最后一个加价的人获得拍卖品,并支付其报价。分配原则:价高者得,支付规则:自己的报价,报价方式:公开报价加价。注意:在这个过程中竞买人知道了其他竞买人的价格。古董和艺术品拍卖常用这种形式。
2)公开减价拍卖(荷兰式拍卖):出售者从一个很高的价格不断减价,直到有竞买者购买,并支付当前价格。因荷兰的郁金香拍卖得名,许多农产品常采用这种形式,拍卖速度比较快。注意虽然公开拍卖,但在这个过程中竞买人仅知道最终的成交价格,并不知道其他竞买人的心理价格。
3)第一价格密封拍卖(FP):竞买者秘密地向出售者提供一个报价,不让其他竞买者知道,价高者得,支付其报价。
4)第二价格密封拍卖(SP):竞买者秘密地向出售者提供一个报价,不让其他竞买者知道,价高者得,支付不是价高者的报价,而是第二高的报价。
这四种形式并非涵盖所有的拍卖形式,但是大部分拍卖是其延伸或者扩展。拍卖的形式有很多种,对于买卖双方来说,都想需求一个最好的形式。这就需要有指标来衡量不同拍卖形式的好坏,指标主要有两个:一个是拍卖效率(也有叫社会效率,社会福利等),这里是指拍卖品被愿意出最高价的竞买者拍到,另一个是卖者的收益,卖者期望的是拍卖收益最大。需要特别指出的,拍卖效率和平台收益有时候不可兼得。
(四)
虽然说拍卖的历史非常悠久,但选择哪种拍卖形式,拍卖效率最大,卖者收益最大呢?直到1961年,威廉·维克里(William Vickrey)针对这几种拍卖形式进行了数学建模,提出了一个独立私人价值模型(IIPV),才得到了一些很重要的结论,也因此获得1996年的诺贝尔经济学奖。

既然是数学建模,那么必定有前提假设条件了。
首先是单物品建模:这个物品不可分割售卖,这是最简单的拍卖形式。(这里特别说明一下:在真实的广告位或者关键词拍卖中,有时候是以多物品拍卖的形式进行的,单物品拍卖下得到的结论不一定适用于多物品拍卖)。
其次是私有估值,并且是独立、对称估值:在这个单物品拍卖中,存在多个竞买者,他们对拍卖物品的估值仅仅依赖于自身的私人信息,不受他人信息影响。(如果受到他人影响,这个估值不再是私人估值,而是关联估值)。独立对称估值是指竞价者估值是相互独立的随机变量,并遵循同一个连续随机变量的概率分布。竞买人除了知道自己的估价外,对于价值分布也完全清楚,只是不知道其他人具体的值。另外竞拍的人数也是共同的知识。
然后是个体理性:估值为0的竞买人其预期支付也为0(拍卖胜出的支付不会超过其出价)
最后是风险中性:竞买人在拍卖中的目标是最大化自己的预期收益,即:预期收益 = 胜出的概率 * (估值 - 胜出计费)- (1- 胜出的概率) * 失败的付费。注意该预期收益是加性可分离的,也就是说不受预算限制、ROI限制等等影响。
(五)
基于IIPV模型,我们来分析一下四种基础拍卖形式下竞买人的竞价策略,均衡状态及其在均衡时的社会效率和卖者收益的情况。因为从竞价策略上分析,荷兰式拍卖与第一价格密封拍卖存在等价策略。在私人价值假设(仅需这一个假设)上,英式拍卖与第二价格密封拍卖存在等价策略。因此来说仅仅分析第一价格密封拍卖和第二价格密封拍卖即可。
这里的策略就是报价。因为竞买人是对称的,所以只用考虑一个典型的竞买人策略,即对于每一个估价v_i选择一个报价b_i,报价策略函数为b_i= B(v_i)。对于一个竞买人来说,他的目的是寻找一个最优报价策略函数B,使得自己的收益最大化。
如果采用第二价格密封拍卖(SP),那么竞买人的最优报价策略函数是什么呢?这里直接给出结论了,竞买人的占优策略就是说出真实报出内心的估价,即b_i = v_i(感兴趣的话可以去看克里斯纳写的《拍卖理论》书中的证明)。最终SP下的均衡是对称占优均衡,社会效率是最大的,因为竞买人真实报出了内心估价,物品又是分配给报价最高的人,对应卖者的收益是次高位的报价。SP的伟大之处在于每个人都在追求私人价值最大化的同时,整体的效率最大化。
如果采用第一价格密封拍卖(FP), FP的报价策略和均衡分析要比SP复杂得多。具体推导过程不再描述(感兴趣可以看《拍卖理论》),这里直接给结果。在FP中,竞买人没有纯占优策略,存在混合策略,即竞买人的均衡报价策略是在假定自己获胜的情况下,对第二高估值的期望值。因此,在均衡的时候,每一个竞买人都会隐藏一部分自己的私人信息,随着参与竞拍人数增加,竞买人的均衡报价将越来越接近其真实估价。所以在FP下的均衡是对称混合纳什均衡,存在社会效率损失的可能。
那么对于售卖者来说,十分迫切地想知道选择哪种拍卖形式可以收益最大化呢?很不幸,Vickrey给出了令人吃惊的答案,这四种拍卖形式对售卖者来说收益是相同的,这就是收益等价原理。
乍一看,第一价格密封拍卖与第二价格密封拍卖的收益应该不一样呀,两者的分配规则是一致的,区别仅在于支付规则,因此采用二价机制很容易遭受损失,但是忘了一个基本问题,因为支付规则不同,两者的分报价策略也是不一样的。前者,竞买者的预期支付依赖于自己的报价,自然会对自己的估价有所隐藏;后者的预期支付与自己的报价无关,会更加积极的报价。
不过,需要注意,虽然存在等价原理,但是并不代表售卖者不需要做决策了。首先,收益等价原理是有前提假设的,即私人价值模型;其次,即使在私人价值模型的前提下,售卖者还有其他的拍卖形式(如全支付拍卖,两阶段拍卖,带有入场费和保留价的拍卖)等可供选择和参数设置,而这部分工作其实也是机制工作的重要部分。
比如,第二价格拍卖下的收益,要比第一价格拍卖下的更加多变,前者的价格区间为整个策略集合,也就是说前者的拍卖风险更大,对于风险厌恶的售卖者来说都会相对偏爱后者,这也就解释了现实生活着的艺术品等大部分采用了第一价格拍卖。
(六)
对于研究者,最重要的能力是建模的能力,就是思考怎么用数学语言,计算机语言描述世界的能力,这也正是学习和教育真正需要培养的能力,而很多情况下,我们已经以考试为导向的教育毁得体无完肤,学习的目的不是认知这个世界,而是变成了考试的分数,找到一份体面的工作,这是一件多么悲哀的事情啊!如今已经毕业多年,在工作中,良师益友难寻,也最需要这样一份能力,还需要一遍遍看书去领悟。我们下篇文章继续介绍,GFP, GSP,以及万剑归宗的第一层口诀心法:排序变换与收益最大化。敬请关注。
参考资料:
[1] 戎文晋 【关键词拍卖与理论实践】
[2] 克里斯纳,罗德明翻译【拍卖理论】
相关文章:

漫谈广告机制设计 | 万剑归宗:聊聊广告机制设计与收入提升的秘密(3)
书接上文漫谈广告机制设计 | 万剑归宗:聊聊广告机制设计与收入提升的秘密(2),我们聊到囚徒困境是完全信息静态博弈,参与人存在占优策略,最终达到占优均衡,并且是对称占优均衡。接下来我们继续…...

安装系统时无raid驱动处理办法
场景描述 安装系统时可以进入安装界面,但是无法识别到硬盘,查看服务器硬件均无异常且从bios或者raid配置界面中能正常看到raid信息及硬盘信息,运行lspci 命令查看到服务器有raid卡,但是未加载驱动。 获取驱动程序模块 查看raid…...
ForkLift:macOS文件管理器/FTP客户端
ForkLift 是一款macOS下双窗口的文件管理器,可以代替本地的访达。ForkLift同时具备连接Ftp、SFtp、WebDav以及云服务器。 ForkLift还具备访达不具备的小功能,比如从文件夹位置打开终端,显示隐藏文件,制作替换等功能。ForkLift 是一…...

信息系统项目管理师 第四版 第20章 高级项目管理
1.项目集管理 1.1.项目集管理标准 1.2.项目集管理角色和职责 1.3.项目集管理绩效域 2.项目组合管理 2.1.项目组合管理标准 2.2.项目组合管理角色和职责 2.3.项目组合管理绩效域 3.组织级项目管理 3.1.组织级项目管理标准 3.2.业务价值与业务评估 3.3.OPM框架要素 3…...
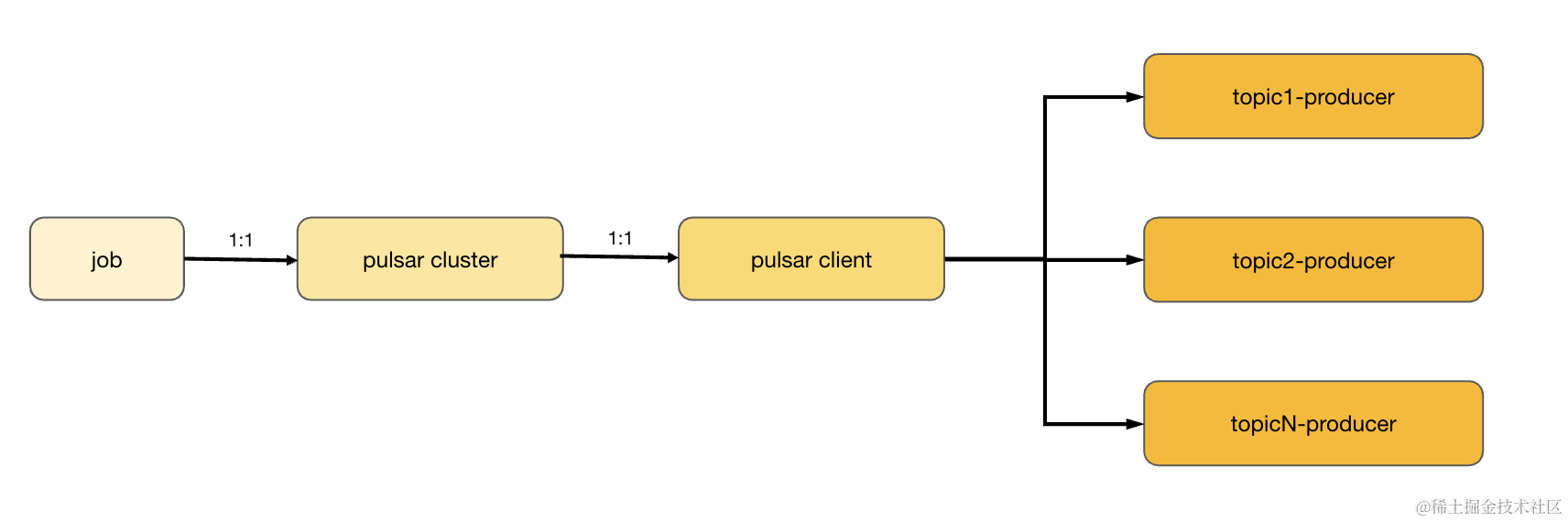
Apache Pulsar 技术系列 - 基于 Pulsar 的海量 DB 数据采集和分拣
导语 Apache Pulsar 是一个多租户、高性能的服务间消息传输解决方案,支持多租户、低延时、读写分离、跨地域复制、快速扩容、灵活容错等特性。本文是 Pulsar 技术系列中的一篇,主要介绍 Pulsar 在海量DB Binlog 增量数据采集、分拣场景下的应用。 前言…...

HDFS、MapReduce原理--学习笔记
1.Hadoop框架 1.1框架与Hadoop架构简介 (1)广义解释 从广义上来说,随着大数据开发技术的快速发展与逐步成熟,在行业里,Hadoop可以泛指为:Hadoop生态圈。 也就是说,Hadoop指的是大数据生态圈整…...

PC端使子组件的弹框关闭
子组件 <template><el-dialog title"新增部门" :visible"showDialog" close"close"> </el-dialog> </template> <script> export default {props: {showDialog: {type: Boolean,default: false,},},data() {retu…...
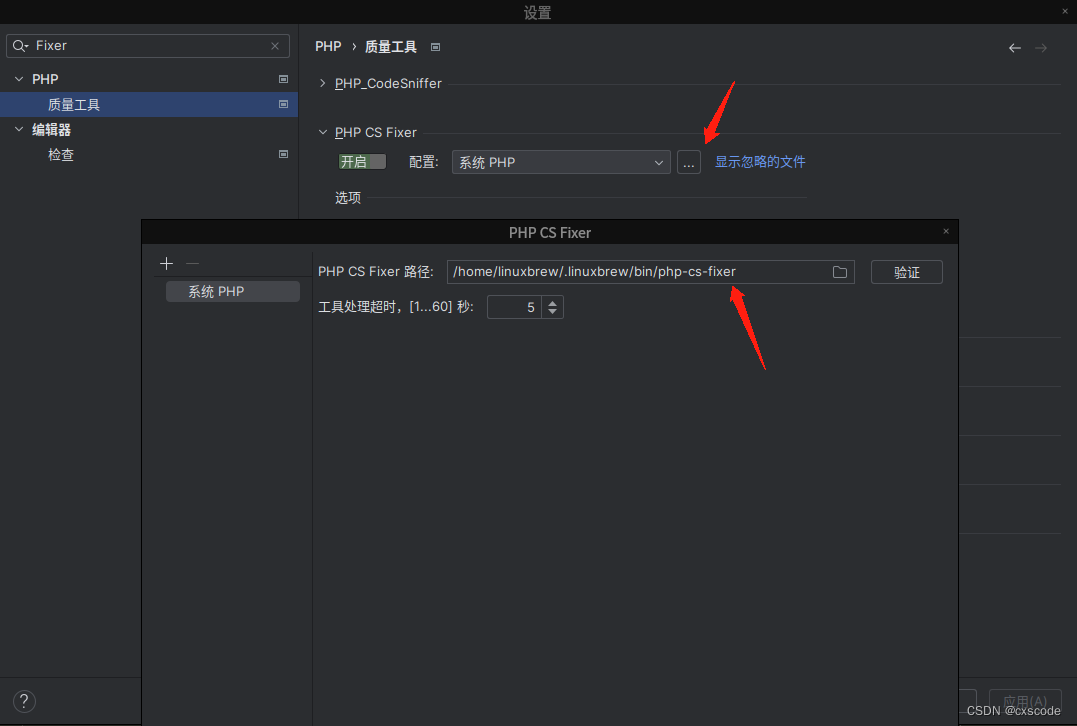
PHPStorm PHP-CS-Fixer
我用的是brew安装: brew install php-cs-fixer phpstorm配置: setting搜索fixer 指定安装php-cs-fixer的目录: https://github.com/PHP-CS-Fixer/PHP-CS-Fixer/blob/master/doc/installation.rst 图文详解PHPStorm实现自动执行代码格式化-…...

SpringBoot中日志的使用log4j
SpringBoot中日志的使用log4j 项目中日志系统是必不可少的,目前比较流行的日志框架有 log4j、logback 等,这两个框架的作者是同一个 人,Logback 旨在作为流行的 log4j 项目的后续版本,从而恢复 log4j 离开的位置。 另外 slf4j(…...

迭代器与生成器
章节目录: 一、迭代器1.1 相关概述1.2 基本使用1.3 自定义迭代器 二、生成器2.1 相关概述2.2 基本使用2.3 三种应用场景 三、yield 和 class 定义的迭代器对比四、结束语 一、迭代器 1.1 相关概述 迭代是 Python 最强大的功能之一,是访问集合元素的一种…...
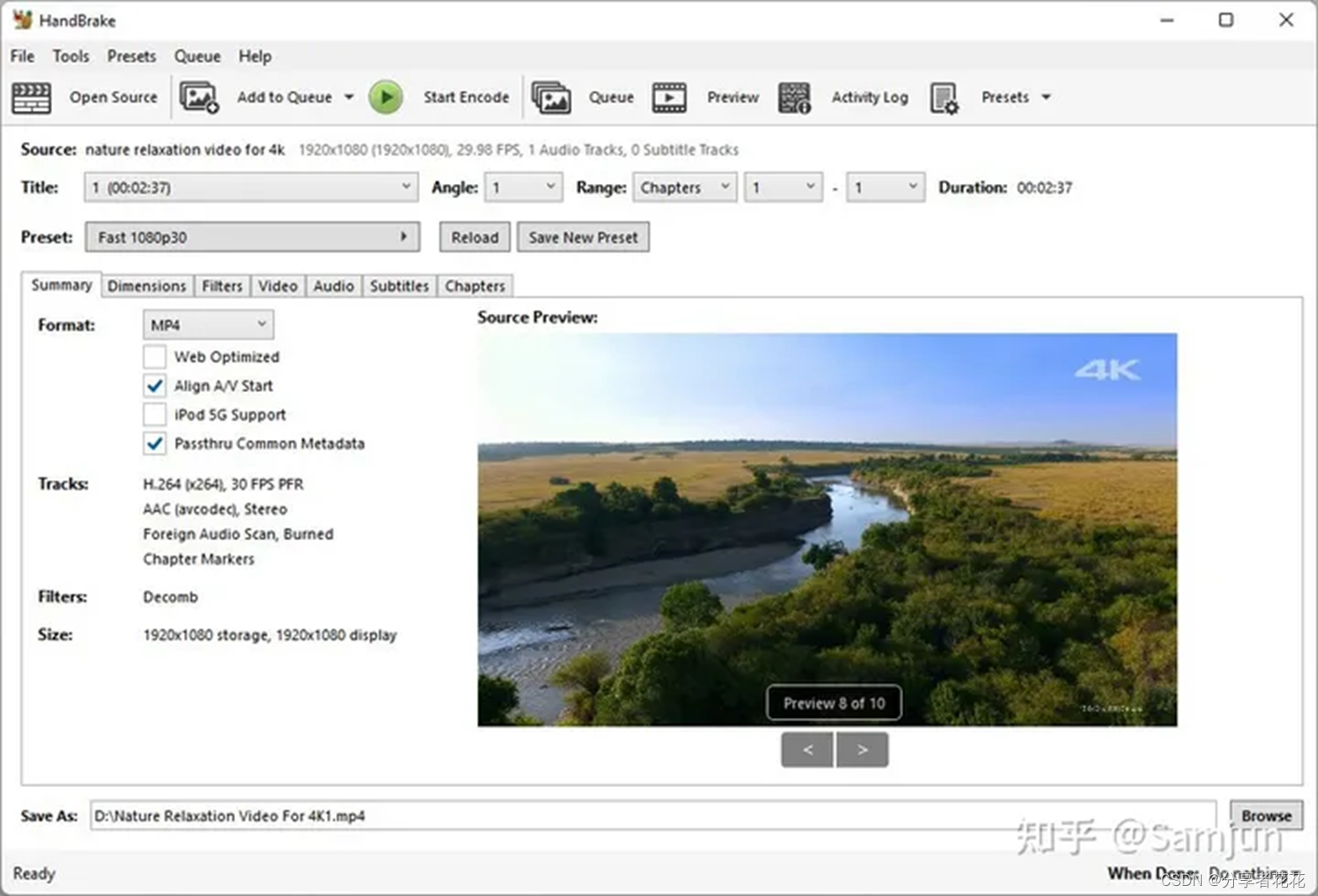
适用于 Windows 的 10 个最佳视频转换器:快速转换高清视频
您是否遇到过由于格式不兼容而无法在您的设备上播放视频或电影的情况?您想随意播放从您的相机、GoPro 导入的视频,还是以最合适的格式将它们上传到媒体网站?您的房间里是否有一堆 DVD 光盘,想将它们转换为数字格式以便于播放&…...

分布式锁的概念、应用场景、实现方式和优缺点对比
一:什么是分布式锁 分布式锁是一种用于协调分布式系统中多个节点对共享资源的访问的机制。在分布式系统中,由于多个节点的并发执行,可能会导致对共享资源的竞争,而分布式锁的目的就是确保在任何时刻,只有一个节点能够持…...

Linux:常见指令
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》 文章目录 前言一、常见指令ls指令pwd指令cd指令touch指令mkdir指令rmdir指令rm指令man指令cp指令mv指令cat指令tac指令echo指令more指令less指令head指令tail指令date显示Cal指令find指令gr…...

大数据基础设施搭建 - ZooKeeper
文章目录 一、上传压缩包二、解压压缩包三、本机安装3.1 修改配置文件3.1.1 创建ZooKeeper数据存储目录3.1.2 修改配置文件名3.1.2 修改配置文件内容 3.3 启动/停止服务端3.4 测试(1)启动客户端(2)测试客户端操作 四、集群安装4.1…...

网站优化工具Google Optimize
Google Optimize 是一款由Google提供的网站优化工具。Google Optimize旨在帮助网站管理员通过对网页内容、设计和布局进行测试和优化,来提升用户体验和网站的转化率。 Google Optimize 提供了 A/B 测试和多变量测试功能,使网站管理员能够比较和评估不同…...

PostgreSQL创建分区表,并插入大量数据
创建分区表,按日期范围分区 CREATE TABLE sales (id serial,sale_date DATE, amount NUMERIC, PRIMARY KEY(id, sale_date) ) PARTITION BY RANGE (sale_date); 创建分区 CREATE TABLE sales_2019 PARTITION OF sales FOR VALUES FROM (2019-0…...

NewStarCTF2023 Reverse Week3 EzDLL WP
分析 这里调用了z3h.dll中的encrypt函数。 用ida64载入z3h.dll 直接搜索encrypt 找到了一个XTEA加密。接着回去找key和密文。 发现key 这里用了个调试状态来判断是否正确,v71,要v7=1才会输出Right,即程序要处于飞调试状态。 可…...
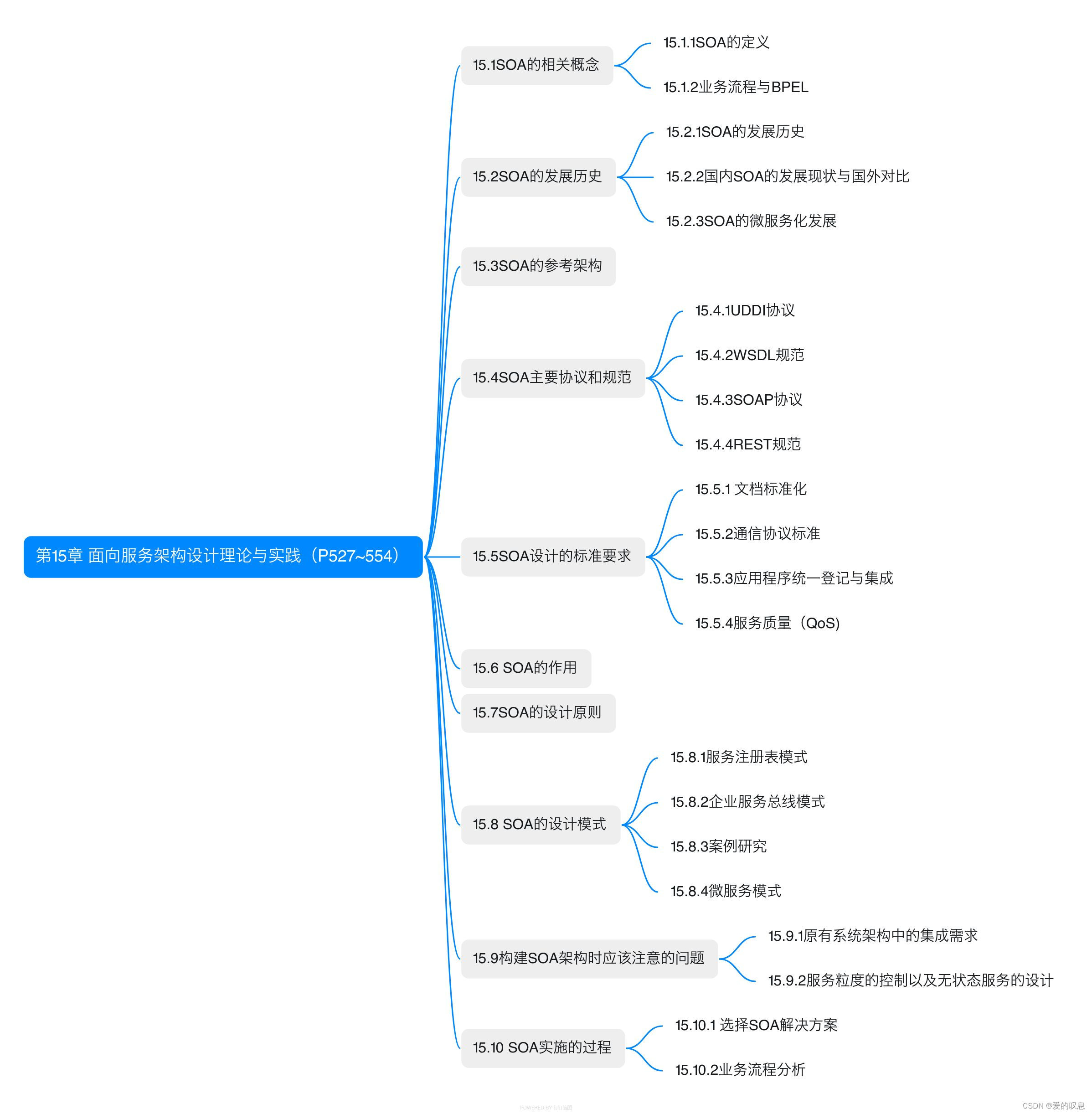
软考-高级-系统架构设计师教程(清华第2版)【第15章 面向服务架构设计理论与实践(P527~554)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第15章 面向服务架构设计理论与实践(P527~554)-思维导图】 课本里章节里所有蓝色字体的思维导图...
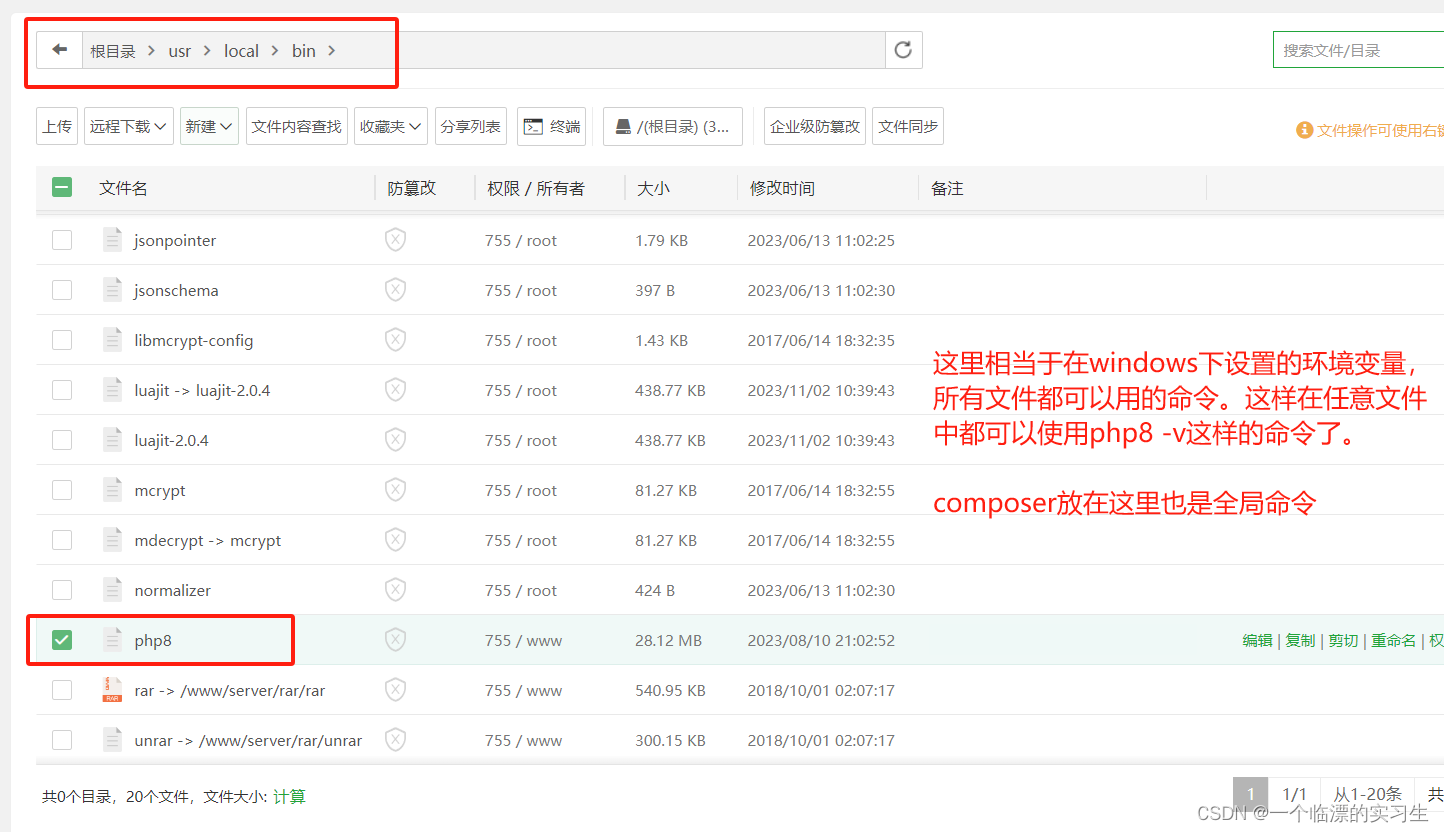
php-cli
//运行index.php ./php index.php//启动php内置服务器 ./php -S 0.0.0.0:8080//启动内置服务在后台运行,日志输出到本目录下的server.log nohup ./php -S 0.0.0.0:8080 -t . > server.log 2>&1 &# 查找 PHP 进程 ps aux | grep "php -S 0.0.0.0:…...
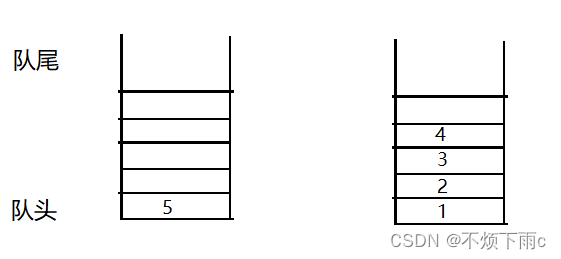
[C/C++] 数据结构 LeetCode:用队列实现栈
题目描述: 请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。 实现 MyStack 类: void push(int x) 将元素 x 压入栈顶。int pop() 移除并返回栈顶元…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
