buu [BJDCTF2020]easyrsa 1
题目描述 :
from Crypto.Util.number import getPrime,bytes_to_long
from sympy import Derivative
from fractions import Fraction
from secret import flagp=getPrime(1024)
q=getPrime(1024)
e=65537
n=p*q
z=Fraction(1,Derivative(arctan(p),p))-Fraction(1,Derivative(arth(q),q))
m=bytes_to_long(flag)
c=pow(m,e,n)
print(c,z,n)
'''
output:
c = 7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
z = 32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
n = 15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441
'''
题目分析:
- 首先这里遇到了两个没见过的函数 ----> Fraction() 和 Derivative()
Fraction(a,b) 相当于 a / b (a 除 b)
Derivative(a,b),前一个参数表示求导的内容,后一个参数表示求导的主体
Derivative(arctan § ,p)的意思是以p为主体对 arctan§ 求导,得到1/(1 + p^2),同理Derivative(arth(q),q) 得到 1/(1 - q^2)
最后
Fraction(1,Derivative(arctan§,p)) = 1 + p^2,Fraction(1,Derivative(arth(q),q) = 1 - q^2
- 得到关系式: z = p^2 +q^2,又 n = p * q,进一步得到关系式 :
(p + q) ^ 2 = z + 2n
(p - q) ^ 2 = z - 2n
用代码解出p,q
import gmpy2
from Crypto.Util.number import *e = 65537
n = 15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441
c = 7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
z = 32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482p = (gmpy2.iroot(z-2*n,2)[0] + gmpy2.iroot(z+2*n,2)[0]) // 2
q = n // p
phi_n = (p-1)*(q-1)
d = gmpy2.invert(e,phi_n)
m = gmpy2.powmod(c,d,n)
print(long_to_bytes(m))
- 得到flag{Advanced_mathematics_is_too_hard!!!}
此题还可以直接用在线网站分解n ,得到p,q,特别简单且快速,比较暴力。但,我喜欢!
收获与体会:
- 又了解了两个新函数:
Fraction(a,b) 相当于 a / b (a 除 b)
Derivative(a,b),前一个参数表示求导的内容,后一个参数表示求导的主体
- 对于有n的,多尝试能否暴力分解得p,q
相关文章:

buu [BJDCTF2020]easyrsa 1
题目描述 : from Crypto.Util.number import getPrime,bytes_to_long from sympy import Derivative from fractions import Fraction from secret import flagpgetPrime(1024) qgetPrime(1024) e65537 np*q zFraction(1,Derivative(arctan(p),p))-Fraction(1,Deri…...

taobao.user.openuid.getbyorder( 根据订单获取买家openuid )
¥免费不需用户授权 根据订单获取买家openuid,最大查询30个 公共参数 请求地址: HTTP地址 http://gw.api.taobao.com/router/rest 公共请求参数: 请求示例 TaobaoClient client new DefaultTaobaoClient(url, appkey, secret); UserOpenuidGetbyorderR…...
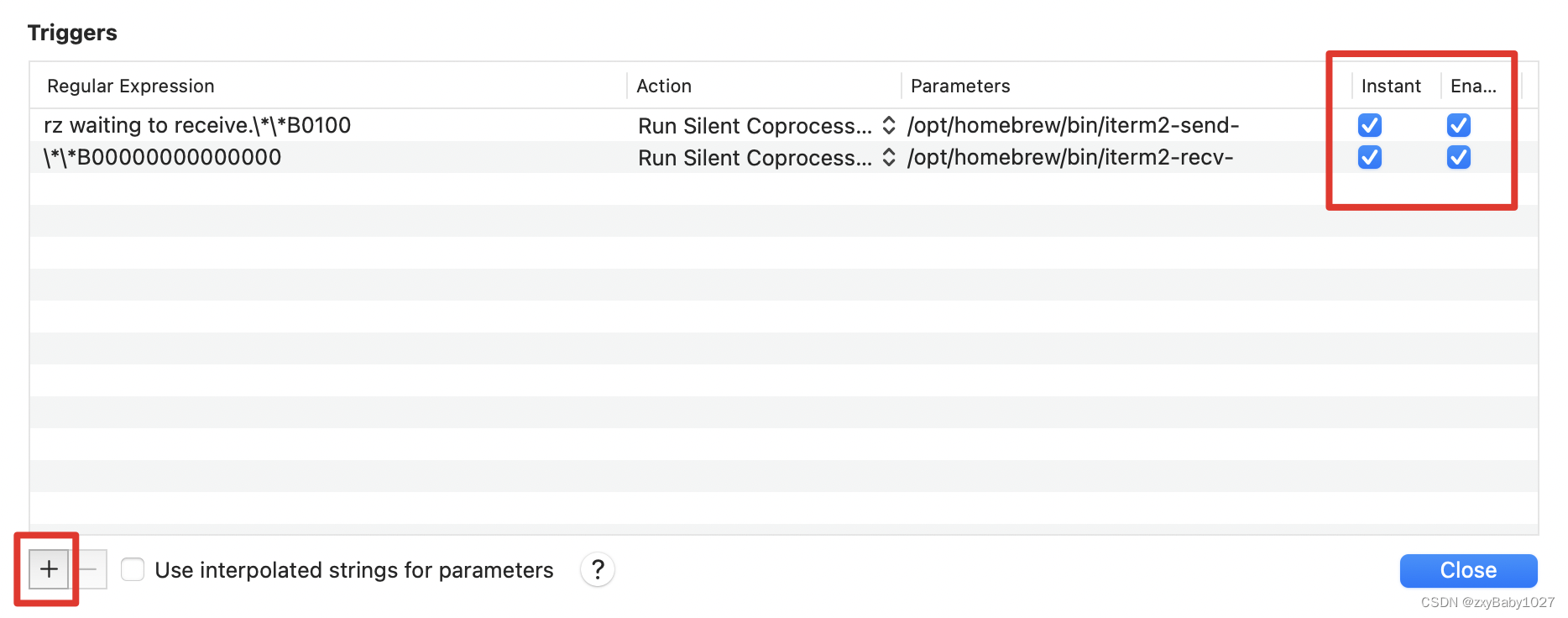
Mac iTerm2 rz sz
1、安装brew(找了很多🔗,就这个博主的好用) Mac如何安装brew?_行走的码农00的博客-CSDN博客_mac brew 2、安装lrzsz brew install lrzsz 检查是否安装成功 brew list 定位lrzsz的安装目录 brew list lrzsz 执…...
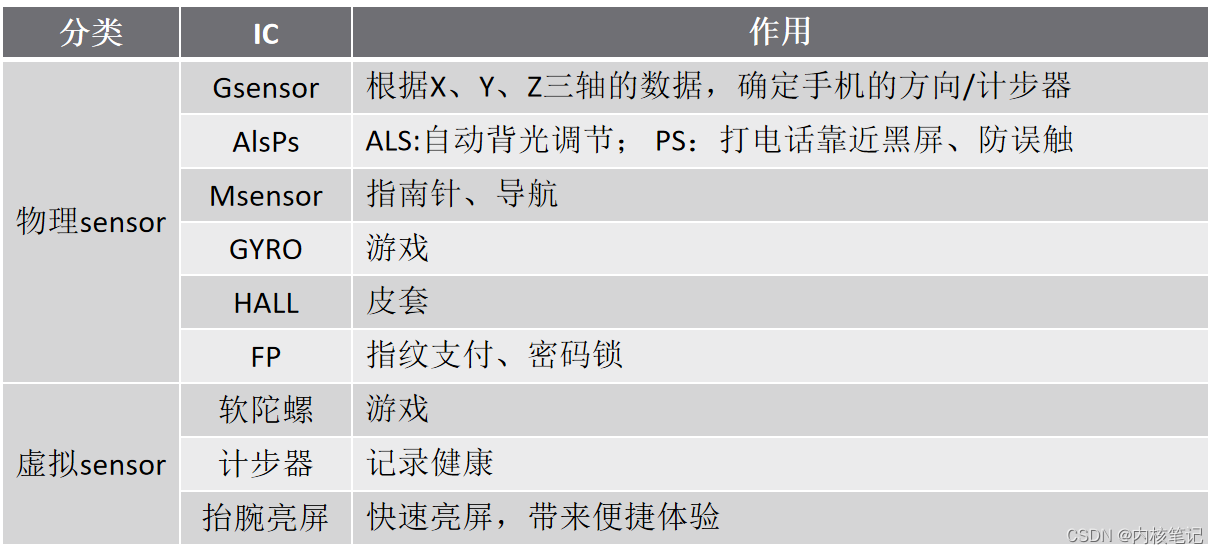
高通平台开发系列讲解(Sensor篇)Gsensor基础知识
文章目录 一、什么是SENSOR?二、Sensor的分类及作用三、Gsensor的工作原理及介绍3.1、常见Gsensor3.2、Gsensor的特性沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍 Sensor 基础 一、什么是SENSOR? 传感器(英文名称:sensor )是一种检测装置,能感…...

图像处理实战--Opencv实现人像迁移
前言: Hello大家好,我是Dream。 今天来学习一下如何使用Opencv实现人像迁移,欢迎大家一起参与探讨交流~ 本文目录:一、实验要求二、实验环境三、实验原理及操作1.照片准备2.图像增强3.实现美颜功能4.背景虚化5.图像二值化处理6.人…...
OnlyOffice验证(二)在Centos7上部署OnlyOffice编译结果
在Centos7上部署OnlyOffice编译结果 此处将尝试将OnlyOffice验证(一)DocumentServer编译验证的结果部署到Centos7上。并且使用其它服务器现有的RabbitMq和Mysql。 安装Nginx 先安装Nginx需要的依赖环境: yum install openssl* -y yum insta…...

6.补充和总结【Java面试第三季】
6.补充和总结【Java面试第三季】前言推荐6.补充和总结69_总结闲聊回顾和总结继续学习最后前言 2023-2-4 19:08:01 以下内容源自 【尚硅谷Java大厂面试题第3季,跳槽必刷题目必扫技术盲点(周阳主讲)-哔哩哔哩】 仅供学习交流使用 推荐 Jav…...

基于ssm框架大学生社团管理系统(源码+数据库+文档)
一、项目简介 本项目是一套基于ssm框架大学生社团管理系统,主要针对计算机相关专业的正在做bishe的学生和需要项目实战练习的Java学习者。 包含:项目源码、数据库脚本等,该项目可以直接作为bishe使用。 项目都经过严格调试,确保可…...
vulnhub靶场NAPPING: 1.0.1教程
靶场搭建靶机下载地址:Napping: 1.0.1 ~ VulnHub直接解压双击ova文件即可使用软件:靶机VirtualBox,攻击机VMware攻击机:kali信息收集arp-scan -l上帝之眼直接来看看网站可以注册账号,那就先试试。注册完后登入哦。要输…...

Docker基本介绍
最近需要将项目做成一个web应用并部署到多台服务器上,于是就简单学习了一下docker,做一下小小的记录。 1、简单介绍一下docker 我们经常遇到这样一个问题,自己写的代码在自己的电脑上运行的很流畅,在其他人电脑上就各种bug&…...
可用于标记蛋白质216699-36-4,6-ROX,SE,6-羧基-X-罗丹明琥珀酰亚胺酯
一.6-ROX,SE产品描述:6-羧基-X-罗丹明琥珀酰亚胺酯(6-ROX,SE)是一种用于寡核苷酸标记和自动DNA测序的荧光染料,可用于标记蛋白质,寡核苷酸和其他含胺分子的伯胺(-NH2)。西…...

高数:极限的定义
目录 极限的定义: 数列极限的几何意义: 由极限的定义得出的极限的两个结论: 编辑 极限的第三个结论: 例题 方法1: 编辑 方法2: 编辑 方法3: 编辑 极限的定义: 如何理…...
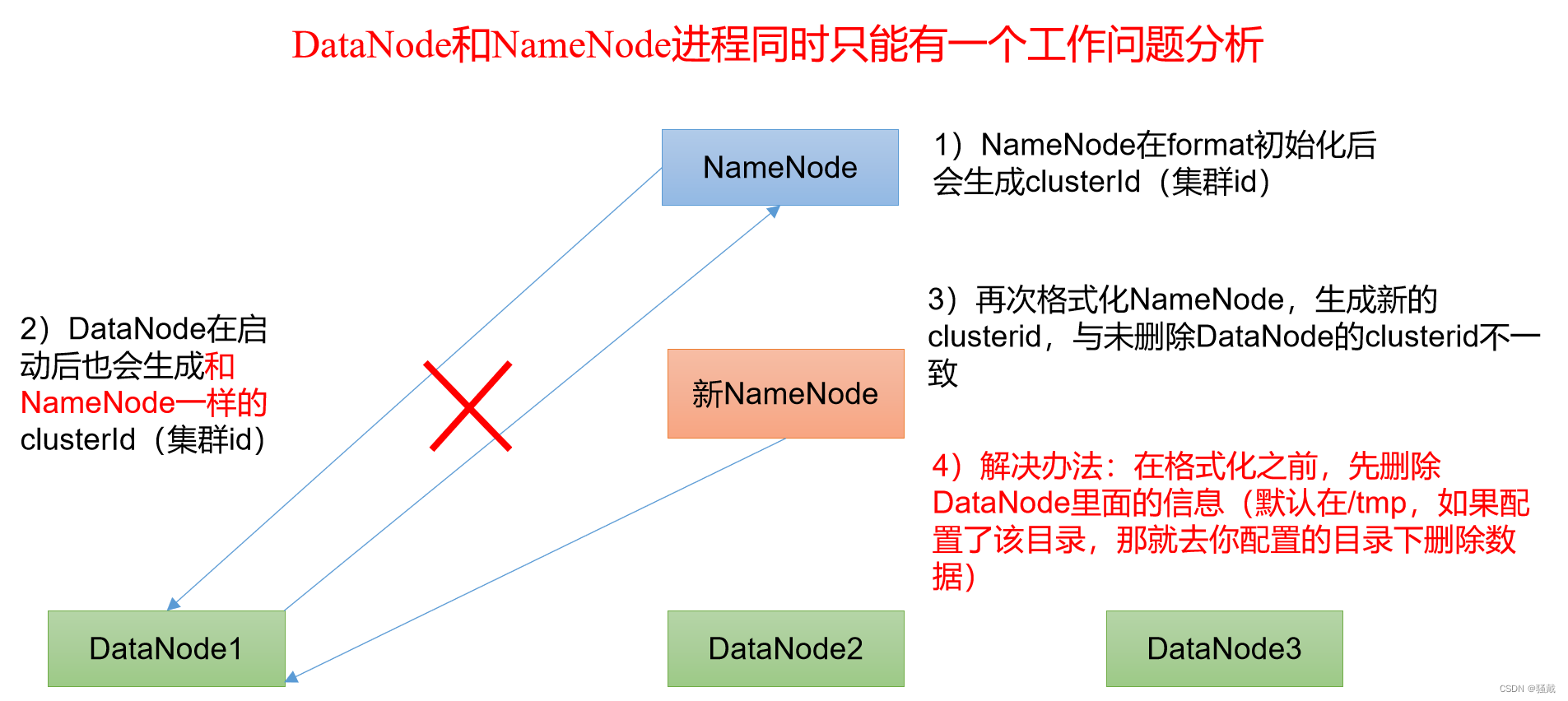
大数据技术之Hadoop
第1章 Hadoop概述1.1 Hadoop是什么1.2 Hadoop发展历史(了解)1.3 Hadoop三大发行版本(了解)Hadoop三大发行版本:Apache、Cloudera、Hortonworks。Apache版本最原始(最基础)的版本,对于…...

一文带你搞懂Go语言函数选项模式,Go函数一等公民。
前言 通过这篇文章《为什么说Go的函数是”一等公民“》,我们了解到了什么是“一等公民”,以及都具备哪些特性,同时对函数的基本使用也更加深入。 本文重点介绍下Go设计模式之函数选项模式,它得益于Go的函数是“一等公民”&#…...
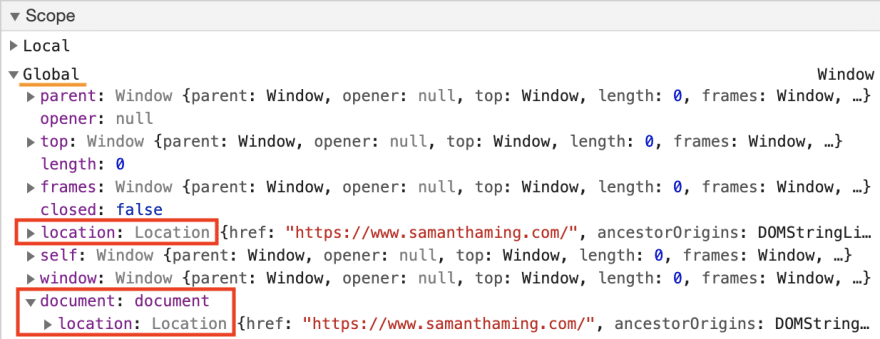
Window.location 详细介绍
如果你需要获取网站的 URL 信息,那么 window.location 对象就是为你准备的。使用它提供的属性来获取当前页面地址的信息,或使用其方法进行某些页面的重定向或刷新。 https://www.samanthaming.com/tidbits/?filterJS#2 window.location.origin → htt…...

js侧滑显示删除按钮
效果图: <!DOCTYPE html> <html><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0, maximum-scale1.0, user-scalableno"><title>js侧滑显示删…...

Python - DIY - 使用dump取json某些键值对合成新的json文件
Python - Json处理前言:应用场景:基本工具:文件操作:打开文件:写文件:读文件:关闭文件并刷新缓冲区:Json字符串和字典转换:json.loads():json.dumps():Json文…...

深度剖析指针(中)——“C”
各位CSDN的uu们你们好呀,今天小雅兰的内容仍旧是深度剖析指针噢,在上一篇博客中,我已经写过了字符指针、数组指针、指针数组、数组传参和指针传参的知识点,那么这篇博客小雅兰会讲解一下函数指针、函数指针数组 、指向函数指针数组…...
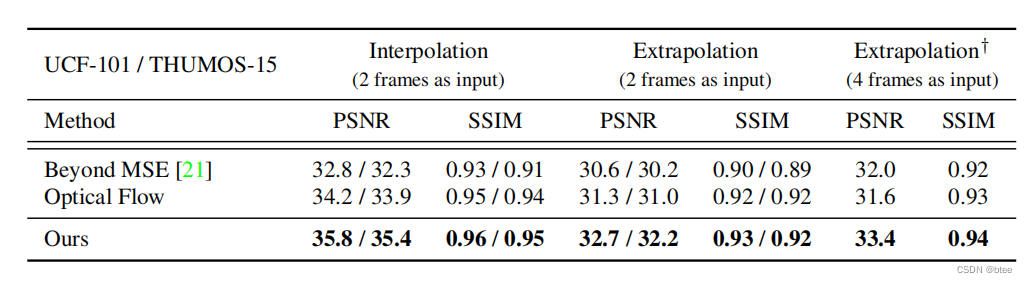
论文阅读 | Video Frame Synthesis using Deep Voxel Flow
前言: 视频帧生成方法(视频插帧/视频预测)ICCV2017 oral Video Frame Synthesis using Deep Voxel Flow 引言 当下进行视频帧合成的方法分为两种,第一种是光流法,光流准确的话效果好,光流不准确的话则生…...

我所理解的生活
诞生 人真正意义上的诞生应该是社会学意义上的,是一种意识到自我、自我与社会关系的存在,只有这种诞生,才是完整人生的基点,大千世界中,唯有人类以生活作为自己的存在方式,除人类以外,从无机界…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
