坐标系下的运动旋量转换
坐标系下的运动旋量转换
文章目录
- 坐标系下的运动旋量转换
- 前言
- 一、运动旋量
- 物体运动旋量
- 空间运动旋量
- 二、伴随变换矩阵
- 三、坐标系下运动旋量的转换
- 四、力旋量
- 五、总结
- 参考资料
前言
对于刚体而言,其角速度可以写为 ω ^ θ ˙ \hat {\omega} \dot \theta ω^θ˙,其中, ω ^ \hat\omega ω^为单位转轴, θ ˙ \dot \theta θ˙为绕着转轴转动的角速度大小。运动旋量则用来描述物体角速度与线速度的组合。由于在机器人学中,运动旋量可能需要描述在不同坐标系之下,本文参考凯文·M.林奇的《现代机器人学》,对运动旋量概念与坐标系下的运动旋量转换进行梳理与总结,便于自己后续回忆。
一、运动旋量
首先,定义有单位螺旋轴 S = ( ω , v x , v y , v z ) ( ω = 1 ) S=(\omega,v_x,v_y,v_z)(\omega=1) S=(ω,vx,vy,vz)(ω=1),利用旋转速度 θ ˙ \dot\theta θ˙与之相乘,由此可得运动旋量 V = S θ ˙ V=S\dot\theta V=Sθ˙。这里注意:通过绕螺旋轴 S S S转动 θ \theta θ角的位移与以速度 θ ˙ = θ \dot\theta=\theta θ˙=θ绕螺旋轴 S S S转动单位时间完全相等,因此, V = S θ ˙ V=S\dot\theta V=Sθ˙可同样看作为指数坐标(刚体转动的指数坐标,可以等效为单位转轴 ω ^ ( ω ^ ∈ R 3 , ∣ ∣ ω ^ ∣ ∣ = 1 ) \hat\omega(\hat\omega\in R^3,||\hat\omega||=1) ω^(ω^∈R3,∣∣ω^∣∣=1))与绕该轴线的转角 θ ∈ R \theta\in R θ∈R。

在对运动旋量有了大致了解以后,正式进入正题,即何为物体运动旋量、何为空间运动旋量。
物体运动旋量
首先,用 { s } \{s\} {s}与 { b } \{b\} {b}分别描述固定(空间)坐标系和移动(物体)坐标系。则有
T s b ( t ) = [ R ( t ) p ( t ) 0 1 ] T_{sb}(t)=\begin{bmatrix} R(t) & p(t) \\ \pmb0 & 1 \end{bmatrix} Tsb(t)=[R(t)0p(t)1]
其中, T s b T_{sb} Tsb表示从空间坐标系到物体坐标系的转换集合矩阵,后续可用 T T T代替。令 T − 1 T ˙ T^{-1}\dot T T−1T˙,则有
T − 1 T ˙ = [ R T − R T p 0 1 ] [ R ˙ p ˙ 0 0 ] = [ R T R ˙ R T p ˙ 0 1 ] T^{-1}\dot T=\begin{bmatrix} R^T & -R^Tp \\ \pmb0 & 1 \end{bmatrix}\begin{bmatrix} \dot R & \dot p \\ \pmb0 & 0 \end{bmatrix}=\begin{bmatrix} R^T\dot R & R^T\dot p \\ \pmb0 & 1 \end{bmatrix} T−1T˙=[RT0−RTp1][R˙0p˙0]=[RTR˙0RTp˙1]
其中, R T R ˙ = R − 1 R ˙ = [ ω b ] R^T\dot R=R^{-1}\dot R=[\omega_b] RTR˙=R−1R˙=[ωb],这里的 [ ω b ] [\omega_b] [ωb]即为物体坐标系 { b } \{b\} {b}下的刚体角速度的反对称矩阵, [ ∗ ] [*] [∗]符号代表 ∗ * ∗的反对称矩阵。具体证明过程可参考书籍,这里不再展开。同理, p ˙ \dot p p˙代表坐标系 { s } \{s\} {s}中描述的 { b } \{b\} {b}的原点的线速度,因此, R T p ˙ = R − 1 p ˙ = v b R^T\dot p=R^{-1}\dot p=v_b RTp˙=R−1p˙=vb则为在物体坐标系 { b } \{b\} {b}中描述 { s } \{s\} {s}的原点的线速度。可进一步阐述为: T − 1 T ˙ T^{-1}\dot T T−1T˙表示动坐标系相对于当前与其瞬时重合的静坐标系 { b } \{b\} {b}的线速度与角速度。
构造六维向量 V b = [ ω b v b ] V_b=\begin{bmatrix} \omega_b \\ v_b \end{bmatrix} Vb=[ωbvb],定义其为物体坐标系中的速度,简称为物体运动旋量。写为矩阵形式为
T − 1 T ˙ = [ V b ] = [ [ ω b ] v b 0 1 ] ∈ s e ( 3 ) T^{-1}\dot T=[V_b]=\begin{bmatrix} [\omega_b] & v_b \\ \pmb0 & 1 \end{bmatrix} \in se(3) T−1T˙=[Vb]=[[ωb]0vb1]∈se(3)
这里可以注意,六维向量 V b V_b Vb的反对称矩阵的撰写形式,即原部矢量 w b w_b wb取反对称形式,偶部矢量不改变形式。
空间运动旋量
同理,可以推导 T ˙ T − 1 \dot TT^{-1} T˙T−1有
V s = [ ω s v s ] ∈ R 6 , T ˙ T − 1 = [ V s ] = [ [ w s ] v s 0 1 ] ∈ s e ( 3 ) V_s=\begin{bmatrix} \omega_s \\ v_s \end{bmatrix} \in R^6, \dot TT^{-1}=[V_s]=\begin{bmatrix} [w_s] & v_s \\ \pmb0 & 1 \end{bmatrix} \in se(3) Vs=[ωsvs]∈R6,T˙T−1=[Vs]=[[ws]0vs1]∈se(3)
此时, V s V_s Vs描述空间固定坐标系中的速度,因此被称为空间运动旋量。
二、伴随变换矩阵
在第一节中,描绘了分别在两个坐标系下的运动旋量,即 V b V_b Vb与 V s V_s Vs,那么,如果我们已知这两个坐标系的转换矩阵 T s b = ( R s b , p s b ) ∈ S E ( 3 ) T_{sb}=(R_{sb},p_{sb})\in SE(3) Tsb=(Rsb,psb)∈SE(3),我们是否可以对这两个运动旋量建立联系呢?答案就是伴随变换矩阵。即有
V s = [ ω s v s ] = [ A d T s b ] V b = [ R s b 0 [ p s b ] R s b R s b ] [ ω b v b ] V_s=\begin{bmatrix} \omega_s \\ v_s \end{bmatrix}=[Ad_{T_{sb}}]V_b=\begin{bmatrix} R_{sb} & \pmb 0\\ [p_{sb}]R_{sb} & R_{sb} \end{bmatrix} \begin{bmatrix} \omega_b \\ v_b \end{bmatrix} Vs=[ωsvs]=[AdTsb]Vb=[Rsb[psb]Rsb0Rsb][ωbvb]
其中, [ A d T s b ] = [ R s b 0 [ p s b ] R s b R s b ] ∈ R 6 × 6 [Ad_{T_{sb}}]=\begin{bmatrix} R_{sb} & \pmb 0\\ [p_{sb}]R_{sb} & R_{sb} \end{bmatrix} \in R^{6\times6} [AdTsb]=[Rsb[psb]Rsb0Rsb]∈R6×6即为该伴随变换矩阵。
将其化为矩阵形式,则有
[ V s ] = T s b [ V b ] T − 1 [V_s]=T_{sb}[V_b]T^{-1} [Vs]=Tsb[Vb]T−1
三、坐标系下运动旋量的转换
结合第二、三节内容,即可总结空间、物体坐标系下运动旋量的转换关系: T s b ( t ) = T ( t ) = [ R ( t ) p ( t ) 0 1 ] ∈ S E ( 3 ) T_{sb}(t)=T(t)=\begin{bmatrix} R(t) & p(t)\\ \pmb0 & 1 \end{bmatrix}\in SE(3) Tsb(t)=T(t)=[R(t)0p(t)1]∈SE(3)仍表示固定坐标系 { s } \{s\} {s}到物体坐标系 { b } \{b\} {b}的位姿转换矩阵(这里的 S E ( 3 ) SE(3) SE(3)即为一种特殊李群)。则有
物体运动旋量(body twist)
T − 1 T ˙ = [ V b ] = [ [ ω b ] v b 0 1 ] ∈ s e ( 3 ) T^{-1}\dot T=[V_b]=\begin{bmatrix} [\omega_b] & v_b \\ \pmb0 & 1 \end{bmatrix} \in se(3) T−1T˙=[Vb]=[[ωb]0vb1]∈se(3)
空间运动旋量(spatial twist)
T ˙ T − 1 = [ V s ] = [ [ ω s ] v s 0 1 ] ∈ s e ( 3 ) \dot TT^{-1}=[V_s]=\begin{bmatrix} [\omega_s] & v_s \\ \pmb0 & 1 \end{bmatrix} \in se(3) T˙T−1=[Vs]=[[ωs]0vs1]∈se(3)
运动旋量 V b V_b Vb与 V s V_s Vs存在关系为
V s = [ ω s v s ] = [ R s b 0 [ p s b ] R s b R s b ] [ ω b v b ] = [ A d T s b ] V b V_s=\begin{bmatrix} \omega_s \\ v_s \end{bmatrix}=\begin{bmatrix} R_{sb} & \pmb 0\\ [p_{sb}]R_{sb} & R_{sb} \end{bmatrix} \begin{bmatrix} \omega_b \\ v_b \end{bmatrix}=[Ad_{T_{sb}}]V_b Vs=[ωsvs]=[Rsb[psb]Rsb0Rsb][ωbvb]=[AdTsb]Vb
V b = [ ω b v b ] = [ R s b T 0 − R s b T [ p s b ] R s b T ] [ ω s v s ] = [ A d T s b ] V s V_b=\begin{bmatrix} \omega_b \\ v_b \end{bmatrix}=\begin{bmatrix} R_{sb}^T & \pmb 0\\ -R_{sb}^T[p_{sb}] & R_{sb}^T \end{bmatrix} \begin{bmatrix} \omega_s \\ v_s \end{bmatrix}=[Ad_{T_{sb}}]V_s Vb=[ωbvb]=[RsbT−RsbT[psb]0RsbT][ωsvs]=[AdTsb]Vs
这里友情提示下,在《现代机器人学》第三次印刷本中,对于 V s V_s Vs到 V b V_b Vb的转换似乎存在小错误,不过问题不大,一般都能看出来,自行矫正即可。
四、力旋量
与运动旋量对应的,也存在着力旋量的定义。对作用于空间物体上的力矩 m a m_a ma与 f a f_a fa,同样可将其合成为六维的空间力的形式,其称为力旋量(wrench),在坐标系 { a } \{a\} {a}中可描述为
F a = [ m a f a ] ∈ R 6 F_a=\begin{bmatrix} m_a \\ f_a \end{bmatrix} \in R^6 Fa=[mafa]∈R6
如若作用于刚体的力旋量不唯一,即将其通过力旋量的六维形式直接相加即可。无力元素的力旋量则被称为纯力偶(pure moment)。
关于力旋量的转换关系,基于系统功率一定原则,最终可推导出:
F b = [ A d T a b T ] F a F_b=[Ad_{T_{ab}}^T]F_a Fb=[AdTabT]Fa
其中, F a F_a Fa与 F b F_b Fb分别为坐标系 { a } \{a\} {a}与坐标系 { b } \{b\} {b}中的力旋量, T a b T_{ab} Tab为坐标系 { a } \{a\} {a}到坐标系 { b } \{b\} {b}的转换矩阵。
五、总结
在学习运动旋量与李群李代数时,一开始感觉确实有些晦涩且难以理解,但是在反复学习时,又感觉其形式简洁且非常实用,因此在这里学习记录,供后续参考。
参考资料
【1】https://www.bilibili.com/video/BV1KV411Z7sC/?p=17&vd_source=029a7426f7a6cecb96f1969e1ce8aff7。
【2】现代机器人学:机构、规划与控制。
相关文章:

坐标系下的运动旋量转换
坐标系下的运动旋量转换 文章目录 坐标系下的运动旋量转换前言一、运动旋量物体运动旋量空间运动旋量 二、伴随变换矩阵三、坐标系下运动旋量的转换四、力旋量五、总结参考资料 前言 对于刚体而言,其角速度可以写为 ω ^ θ ˙ \hat {\omega} \dot \theta ω^θ˙&…...

Android Termux安装MySQL,通过内网穿透实现公网远程访问
🔥博客主页: 小羊失眠啦. 🔖系列专栏: C语言、Linux、Cpolar ❤️感谢大家点赞👍收藏⭐评论✍️ 文章目录 前言1.安装MariaDB2.安装cpolar内网穿透工具3. 创建安全隧道映射mysql4. 公网远程连接5. 固定远程连接地址 前…...

Python in Visual Studio Code 2023年11月发布
排版:Alan Wang 我们很高兴地宣布 Visual Studio Code 的 Python 和 Jupyter 扩展将于 2023 年 11 月发布! 此版本包括以下公告: 改进了使用 Shift Enter 在终端中运行当前行弃用内置 linting 和格式设置功能对 Python linting 扩展的改进重…...
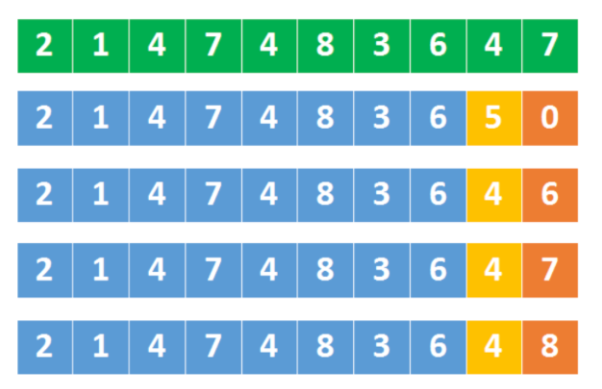
算法通关村——数字中的统计、溢出、进制转换处理模板
数字与数学基础问题 1、数字统计 1.1、符号统计 LeetCode1822. 给定一个数组,求所有元素的乘积的符号,如果最终答案是负的返回-1,如果最终答案是正的返回1,如果答案是0返回0. 这题其实只用看数组中0和负数的个数就好了&#x…...

ESP01S通过心知天气获取天气和时间信息
ESP01S通过心知天气获取天气和时间信息 设置STA模式 ATCWMODE1 连接wifi ATCWJAP"wifi名称","wifi密码"3.设置时间地域 ATCIPSNTPCFG1,8获取时间 ATCIPSNTPTIME?返回: CIPSNTPTIME:Fri Nov 17 17:09:22 2023 OK连接心知服务器 ATCIPSTAR…...

docker容器内core dumped却找不到core文件
1. 检查ulimit, 使用命令: ulimit -a rootb7c19f6da1e3:/usr# ulimit -a core file size (blocks, -c) unlimited data seg size (kbytes, -d) unlimited scheduling priority (-e) 0 file size (blocks…...
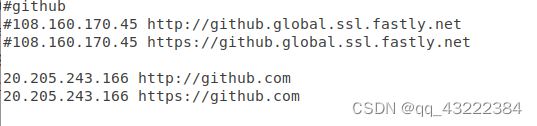
ubuntu提高 github下载速度
Github一般用于Git的远程仓库,由于服务器位于国外,国内访问速度比较慢,为了提高访问速度,决定绕过DNS域名解析。 获取Github的IP地址 按下ctrl+alt+T打开命令终端,输入: nslookup gi…...

Node.js之path路径模块
让我为大家介绍一下path路径模块吧! 什么是path路径模块? path 模块是 Node.s 官方提供的、用来处理路径的模块。它提供了一系列的方法和属性,用来满足用户对路径的处理需求。 介绍三个关于path模块的方法: path.join() 方法&…...

TCP与UDP协议
TCP与UDP协议 1、TCP协议: 1、TCP特性: TCP 提供一种面向连接的、可靠的字节流服务。在一个 TCP 连接中,仅有两方进行彼此通信。广播和多播不能用于 TCP。TCP 使用校验和,确认和重传机制来保证可靠传输。TCP 给数据分节进行排序…...
$/i ”这个正则表达式的理解)
“ /^A-Z:\\{1,2}^/:\*\?<>\|+\.(jpg|gif|png|bmp)$/i ”这个正则表达式的理解
这个正则表达式可以分解为以下几个部分: ^:这是一个开始符号,表示匹配必须从字符串的开始部分开始。/:这是一个斜杠符号,通常在正则表达式中用来表示特殊字符的转义。A-Z::这部分表示匹配一个大写字母后跟…...

批量下载Sentinel数据脚本2023
批量下载Sentinel数据脚本2023 那些最好的程序员不是为了得到更高的薪水或者得到公众的仰慕而编程,他们只是觉得这是一件有趣的事情! 批量下载Sentinel数据脚本2023 批量下载Sentinel数据脚本2023🌿前言🌿脚本地址📧Su…...
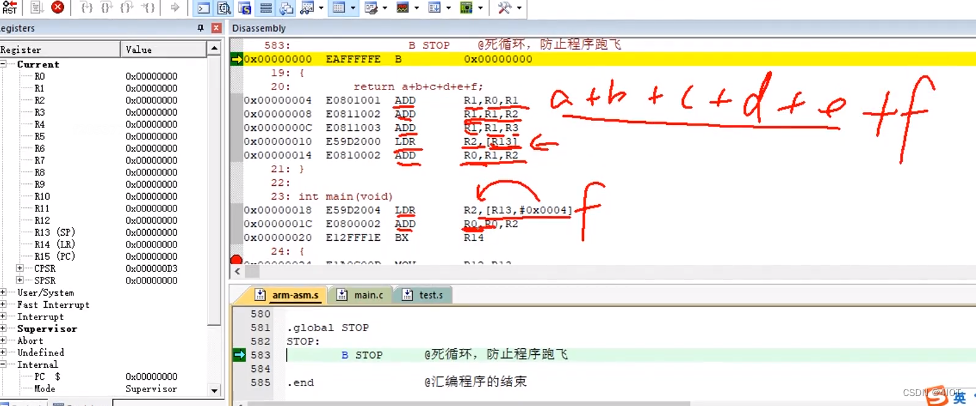
lv11 嵌入式开发 ARM指令集中(伪操作与混合编程) 7
目录 1 伪指令 2 伪操作 3 C和汇编的混合编程 4 ATPCS协议 1 伪指令 本身不是指令,编译器可以将其替换成若干条等效指令 空指令NOP 指令LDR R1, [R2] 将R2指向的内存空间中的数据读取到R1寄存器 伪指令LDR R1, 0x12345678 R1 0x12345678 LDR伪指令可以将任…...

北邮22级信通院数电:Verilog-FPGA(10)第十周实验 实现移位寄存器74LS595
北邮22信通一枚~ 跟随课程进度更新北邮信通院数字系统设计的笔记、代码和文章 持续关注作者 迎接数电实验学习~ 获取更多文章,请访问专栏: 北邮22级信通院数电实验_青山如墨雨如画的博客-CSDN博客 目录 一.代码部分 二.管脚分配 三.实现过程讲解及效…...
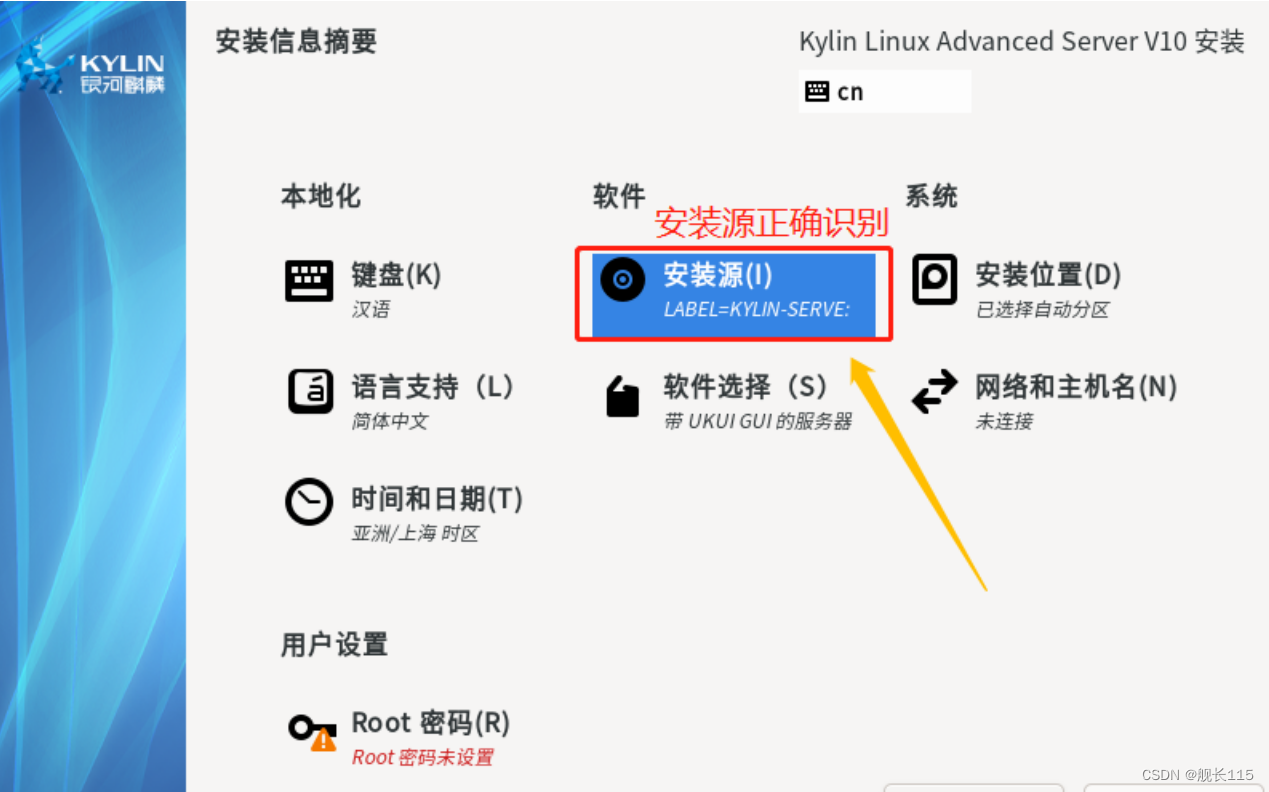
麒麟系统安装找不到安装源!!!!设置基础软件仓库时出错
记录--华为RH2288 V3服务器安装麒麟系统遇到的问题 1.遇到的问题--“设置基础软件仓库时出错”报错导致无法继续安装 没办法下一步 先说结论:系统bug 该问题在CentOS、Rocky Linux最新版中均存在 解决: (一)、如果是外网直接配…...
代码随想录算法训练营第三十九天【动态规划part02】 | 62.不同路径、63. 不同路径 II
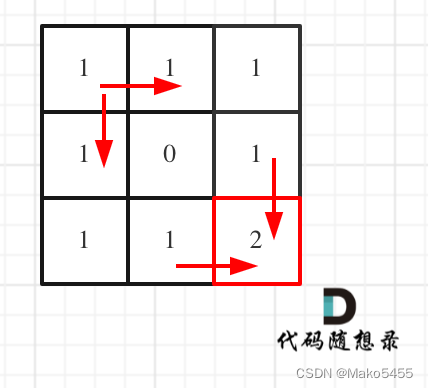
62.不同路径 题目链接: 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 求解思路: 动规五部曲 确定dp数组及其下标含义:dp[i][j] 表示从(0,0)出发,到(i,j&#x…...
鸿蒙4.0开发笔记之DevEco Studio如何使用Previewer窗口预览器(一)
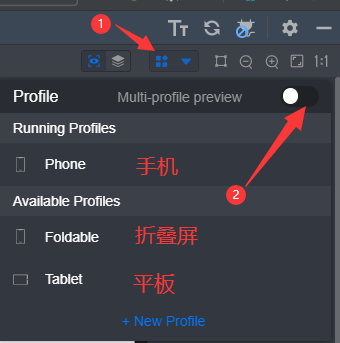
一、预览器作用 DevEco Studio预览器概况在HarmonyOS应用开发过程中,通过使用预览器,可以查看应用的UI效果,方便开发者实时查看应用的运行效果,随时调整代码。 二、打开Previewer预览器 1、正常启动 打开预览器的位置在DevEco…...
音视频转换软件Permute mac中文板特点介绍
Permute mac是一款Mac平台上的媒体格式转换软件,由Chaotic Software开发。它可以帮助用户快速地将各种音频、视频和图像文件转换成所需格式,并提供了一些常用工具以便于用户进行编辑和处理。 Permute mac软件特点 - 支持大量格式:支持几乎所…...

前端uniapp列表下拉到底部加载下一页列表【下拉加载页面/带源码/实战】
目录 一. 图片1.2. 二.list.vue三.uni-load-more.vue最后 一. 图片 1. 2. 二.list.vue <template><view><!--列表--><scroll-view scroll-y"true" class"scroll-Y" :style"height: scrollviewHigh px;" lower-threshol…...
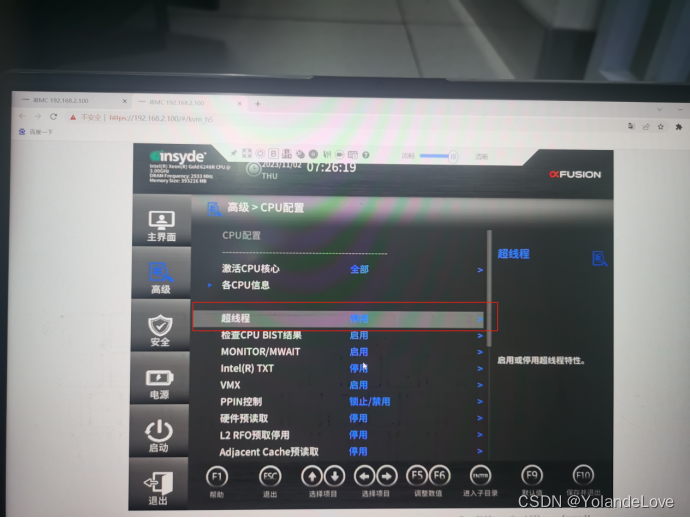
超聚变服务器关闭超线程CPU的步骤(完整版)
前言: 笨鸟先飞,好记性不如烂笔头。 我们项目都用不到超线程CPU,所以调测设备的时候都需要关掉,最近新设备换成了超聚变的服务器,这篇记录我关闭(超聚变)服务器超线程CPU的方法步骤。 关闭超线程CPU的步骤…...
智能驾驶汽车虚拟仿真视频数据理解(一)
赛题官网 datawhale 赛题介绍 跑通demo paddle 跑通demo torch 提交的障碍物取最主要的那个?不考虑多物体提交。障碍物,尽可能选择状态发生变化的物体。如果没有明显变化的,则考虑周边的物体。车的状态最后趋于减速、停止,时序…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
