数据结构 堆
手写堆,而非stl中的堆
如何手写一个堆?
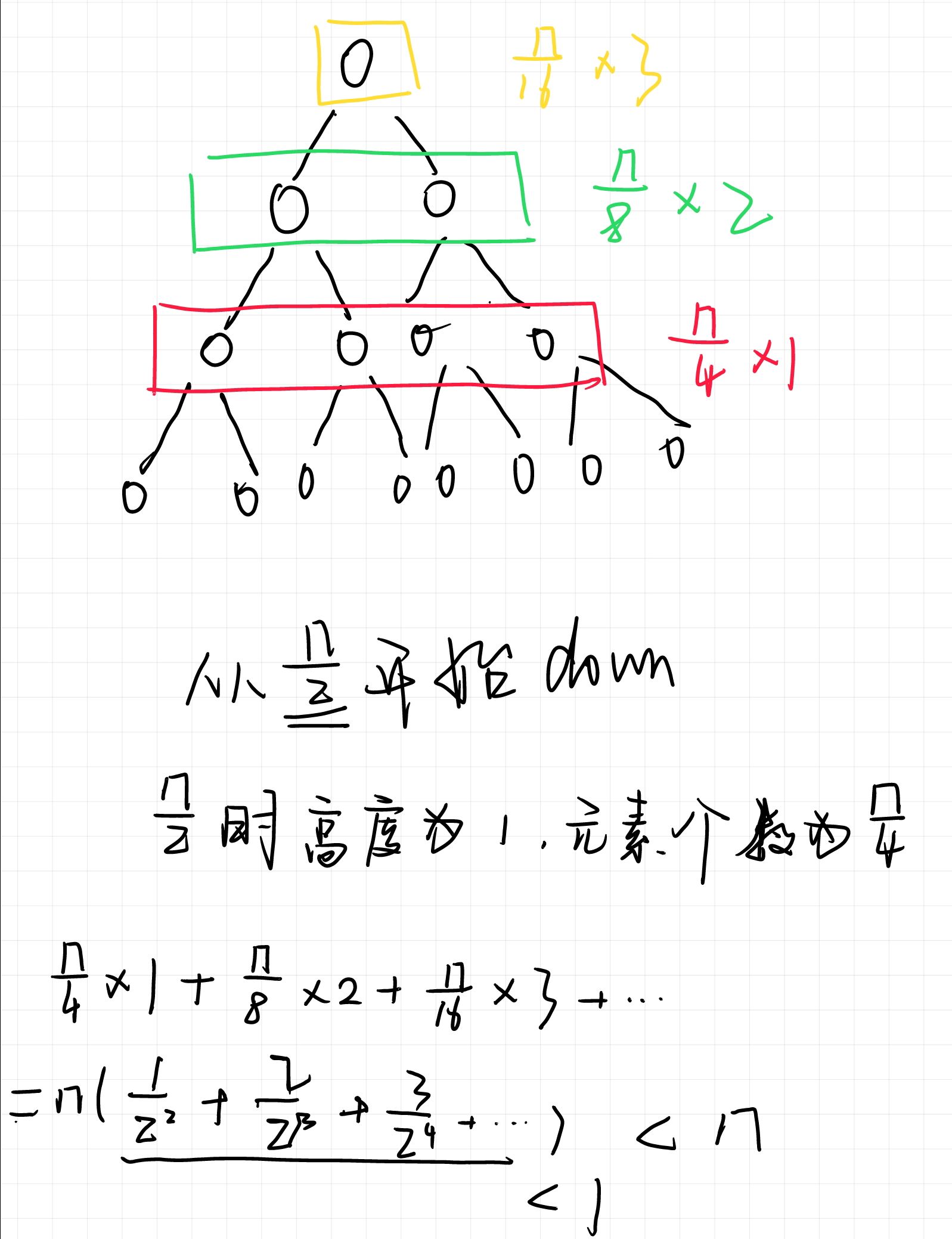
//将数组建成堆 <O(n)
for (int i = n / 2;i;i--) //从n/2开始down
down(i);
从n/2元素开始down,最下面一层元素的个数是n/2,其余上面的元素的个数是n/2,从最下面一层到最高层,每层元素的个数是n/2^m【m从下到上,从1计算,m=1时是最下面一层】,时间复杂度就是元素个数*高度【高度从下到上,从0计算】
性质
1.堆是一棵完全二叉树【除叶子结点之外,所有结点都是非空的】
2.小根堆:每个点的值都是小于等于其左右两个儿子的,根结点就是整个数据中的最小值
静态数组存储——一维数组
用一个一维数组来存,根结点放在数组开头,1号点是根结点,结点x的左儿子下标为2x,右儿子下标为2x+1
两个基本操作
对于所有的堆操作而言,每个操作都可以使用这两个操作构建。
down(x) 向下调整——从下往上down一次就变成一个堆
大数位于上面,需要向下移
每次与其两个儿子进行比较,找到较小的儿子与其进行交换,直到小于所有的儿子为止【该结点的子结点都大于该结点】
//递归实现
void down(int u) {
int t = u;//用t表示三个点中的最小值
if (u * 2 <= size1 && h[u * 2] < h[t])//先判断是否有左儿子,然后判断左儿子是否小于其本身,如果成立,交换
t = u * 2;
if (u * 2 + 1 <= size1 && h[u * 2 + 1] < h[t])//再判断是否有右儿子,然后判断右儿子是否小于其本身,如果成立,交换
t = u * 2 + 1;
//最终,t存的就是三个点中最小的结点编号
if (u != t) {//如果u!=t,说明根结点就不是最小的,需要交换
swap(h[u], h[t]);//交换
down(t);//递归,交换之前h[t]<=h[u],交换之后h[t]>h[u],h[t]中存的是大数,对其再进行down操作,即递归
}
return;
}
up(x) 向上调整
小数位于下面,需要向上移
每次只需要与其根结点比较,如果小于其根结点,就与其根结点进行交换,直到>=其根结点为止
//循环实现
void up(int u) {
while (u / 2 && h[u / 2] > h[u]) {//u的父结点为u/2,父结点存在且大于本身,交换
swap(h[u / 2], h[u]);
u = u / 2;
}
return;
}
操作
【前三最重要】
【下标从1开始】
1.向集合中插入一个数
在整个堆的最后一个位置插入,然后再向上调整
heap[++size]=x;
up(size);
2.求集合中的最小值
heap[1];
3.删除最小值
用整个堆的最后一个元素覆盖掉堆顶的元素,然后size--,然后向下调整
因为删去最后一个结点特别容易,而删除根结点却不易
heap[1]=heap[size];
size--;
down(1);
4.删除任意一个元素
用堆的最后一个结点覆盖该结点,然后size--,然后向下调整(变大)、向上调整(变小),二选一执行
heap[k]=heap[size];
size--;
down(k);//变大
up(k);//变小
5.修改任意一个操作
heap[k]=x;
down(k);//变大
up(k);//变小
例题——堆排序
题目描述
输入一个长度为n的整数数列,从小到大输出前m小的数。
输入格式
第一行包含整数n和m。
第二行包含n个整数,表示整数数列。
输出格式
共一行,包含m个整数,表示整数数列中前m小的数。
数据范围
1≤m≤n≤10^5,
1≤数列中元素≤10^9
输入样例
5 3
4 5 1 3 2
输出样例
1 2 3
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
int n, m;
int h[N], size1;//h[N]就是heap[N],size1存储当前有多少个元素
int main() {
scanf("%d%d", &n, &m);
for (int i = 1;i <= n;i++)
scanf("%d", &h[i]);
size1 = n;
//将数组建成堆 <O(n)
for (int i = n / 2;i;i--) //从n/2开始down
down(i);
while (m--) {
printf("%d ", h[1]);//每次输出堆顶元素,并将其删去
h[1] = h[size1];
size1--;
down(1);
}
return 0;
}
例题——模拟堆[包含映射]
增加两个数组
使用两个数组维护两个映射关系,ph[k] 存第k个插入的点在堆中的下标,hp[k] 存堆中下标为k的点是第几个插入的点
增加的原因
因为按第几个插入元素更改内容,需要知道第i个插入的元素在堆中的下标,所以需要ph的存在,而因为元素在进行down与up操作时,使得ph内容与实际堆的元素不对应,所以要改变ph,而改变ph应该知道,每一个下标对应的插入元素是第几个,所以需要hp的存在。每次交换位置时应该共同维护这两个数组。
交换操作
void heap_swap(int a, int b) {
swap(ph[hp[a]], ph[hp[b]]);//交换指向
swap(hp[a], hp[b]);
swap(h[a], h[b]);
return;
}
交换堆中的两个元素时,hp 和 ph 也改变。先改变 hp 和 ph 中的内容,然后改变这两个结点中的值。先根据交换的下标找到对应的 hp,并以两个 hp 元素值作为 ph 的下标,交换这2个 ph 元素值。之后根据下标交换 hp。
swap(ph[hp[a]], ph[hp[b]]);为什么这里的ph的下标是hp的元素值而不是堆中元素的编号?
因为ph的下标k的含义【即ph[k]的k的含义】是第k个插入的点,所以我们要找到第k个插入的点而不是堆中下标为k的点。
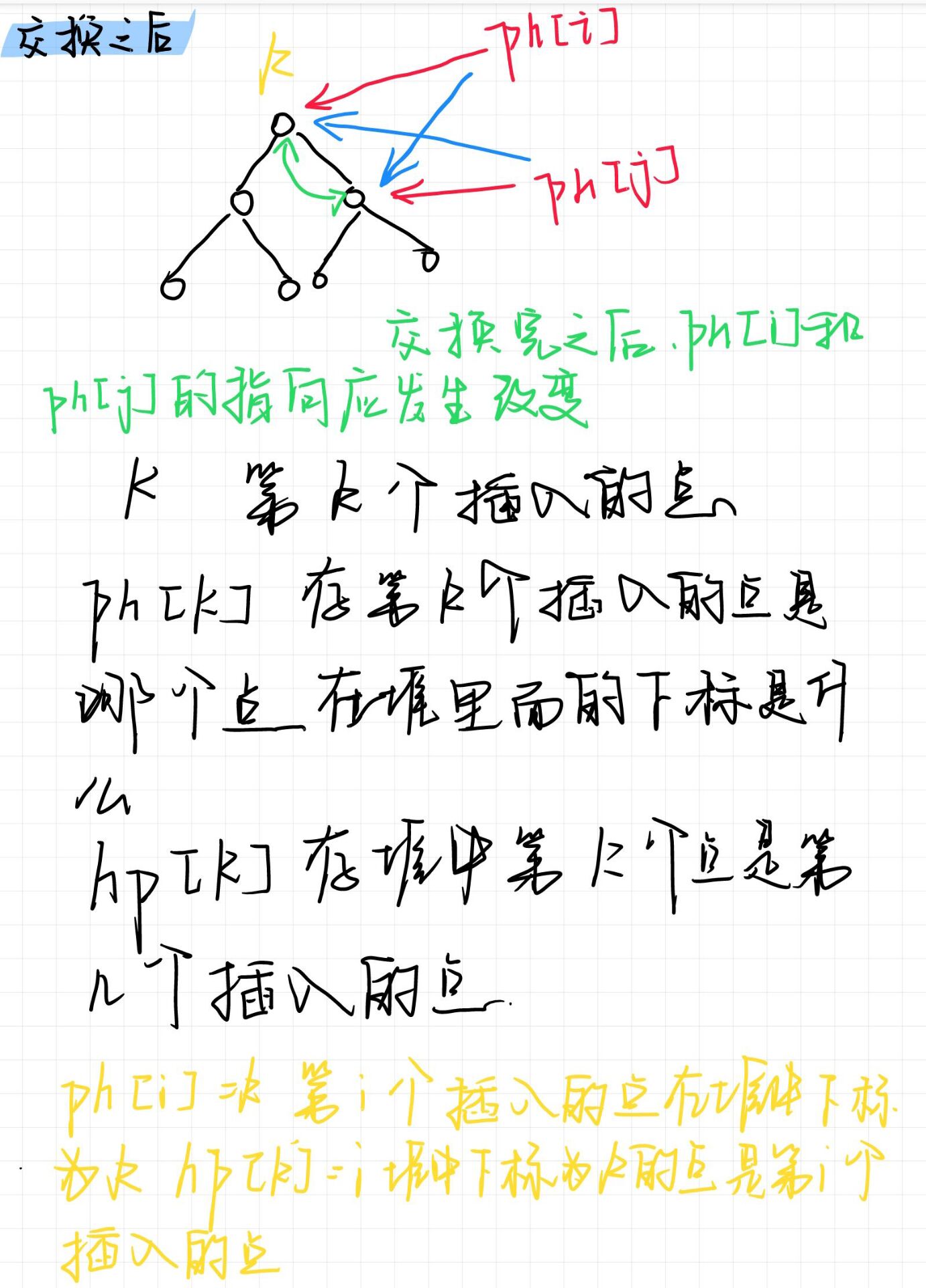
改变后的操作
up 操作
手写的heap_swap函数代替原来的swap函数
void up(int u) {
while (u / 2 && h[u / 2] > h[u]) {//u的父结点为u/2,父结点存在且大于本身,交换
heap_swap(u / 2, u);
u = u / 2;
}
return;
}
down 操作
手写的heap_swap函数代替原来的swap函数
void down(int u) {
int t = u;//用t表示三个点中的最小值
if (u * 2 <= size1 && h[u * 2] < h[t])//先判断是否有左儿子,然后判断左儿子是否小于其本身,如果成立,交换
t = u * 2;
if (u * 2 + 1 <= size1 && h[u * 2 + 1] < h[t])//再判断是否有右儿子,然后判断右儿子是否小于其本身,如果成立,交换
t = u * 2 + 1;
//最终,t存的就是三个点中最小的结点编号
if (u != t) {//如果u!=t,说明根结点就不是最小的,需要交换
heap_swap(u, t);//交换
down(t);
}
return;
}
向集合中插入一个数
添加hp和ph数组中的映射关系
scanf("%d", &x);//向堆中插入x
size1++;
m++;
ph[m] = size1;
hp[size1] = m;
h[size1] = x;
up(size1);
输出集合中的最小值
printf("%d\n", h[1])
删除最小值
手写的heap_swap函数代替原来的swap函数
heap_swap(1, size1);
size1--;
down(1);
删除第k个插入的元素
scanf("%d", &k);//输入k
k = ph[k];//找到第k个插入的元素在堆中的下标,然会对其进行删除
heap_swap(k, size1);//用堆中最后一个元素覆盖找到的元素,然会进行调整
size1--;
down(k), up(k);
修改第k个插入的元素
scanf("%d%d", &k, &x);//输入k和修改后的值x
k = ph[k];//找到第k个插入的元素在堆中的下标,然后修改其值,修改后进行调整
h[k] = x;
down(k), up(k);
题目描述
维护一个集合,初始时集合为空,支持如下几种操作:
“I x”,插入一个数x;
“PM”,输出当前集合中的最小值;
“DM”,删除当前集合中的最小值(当最小值不唯一时,删除最早插入的最小值);
“D k”,删除第k个插入的数;
“C k x”,修改第k个插入的数,将其变为x;
现在要进行N次操作,对于所有第2个操作,输出当前集合的最小值。
输入格式
第一行包含整数N。
接下来N行,每行包含一个操作指令,操作指令为”I x”,”PM”,”DM”,”D k”或”C k x”中的一种。
输出格式
对于每个输出指令“PM”,输出一个结果,表示当前集合中的最小值。
每个结果占一行。
数据范围
1≤N≤10^5
−10^9≤x≤10^9
数据保证合法。
输入样例
8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM
输出样例
-10
6
#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
const int N = 100010;
int h[N], ph[N], hp[N], size1;//h[N]就是heap[N],size1存储当前有多少个元素,ph[k]存第k个插入数组的下标
//ph[j]=k【第j次插入数组的数的下标是k】,hp[k]=j【下标为k的数是第j次插入数组中的数】
void heap_swap(int a, int b) {
swap(ph[hp[a]], ph[hp[b]]);//交换指向
swap(hp[a], hp[b]);
swap(h[a], h[b]);
return;
}
void down(int u) {
int t = u;//用t表示三个点中的最小值
if (u * 2 <= size1 && h[u * 2] < h[t])//先判断是否有左儿子,然后判断左儿子是否小于其本身,如果成立,交换
t = u * 2;
if (u * 2 + 1 <= size1 && h[u * 2 + 1] < h[t])//再判断是否有右儿子,然后判断右儿子是否小于其本身,如果成立,交换
t = u * 2 + 1;
//最终,t存的就是三个点中最小的结点编号
if (u != t) {//如果u!=t,说明根结点就不是最小的,需要交换
heap_swap(u, t);//交换
down(t);
}
return;
}
void up(int u) {
while (u / 2 && h[u / 2] > h[u]) {//u的父结点为u/2,父结点存在且大于本身,交换
heap_swap(u / 2, u);
u = u / 2;
}
return;
}
int main() {
int n, m = 0;
scanf("%d", &n);
while (n--) {
char op[10];
int k, x;
scanf("%s", op);
if (!strcmp(op, "I")) {
scanf("%d", &x);
size1++;
m++;
ph[m] = size1;
hp[size1] = m;
h[size1] = x;
up(size1);
}
else if (!strcmp(op, "PM"))
printf("%d\n", h[1]);
else if (!strcmp(op, "DM")) {
heap_swap(1, size1);
size1--;
down(1);
}
else if (!strcmp(op, "D")) {
scanf("%d", &k);
k = ph[k];
heap_swap(k, size1);
size1--;
down(k), up(k);
}
else {
scanf("%d%d", &k, &x);
k = ph[k];
h[k] = x;
down(k), up(k);
}
}
return 0;
}
相关文章:

数据结构 堆
手写堆,而非stl中的堆 如何手写一个堆? //将数组建成堆 <O(n) for (int i n / 2;i;i--) //从n/2开始down down(i); 从n/2元素开始down,最下面一层元素的个数是n/2,其余上面的元素的个数是n/2,从最下面一层到最高层…...
将 ONLYOFFICE 文档编辑器与 Node.js 应用集成
我们来了解下,如何将 ONLYOFFICE 文档编辑器与您的 Web 应用集成。 许多 Web 应用都可以从文档编辑功能中获益。但是要从头开始创建这个功能,需要花费大量时间和精力。幸运的是,您可以使用 ONLYOFFICE——这是一款开源办公套件,可…...
CentOS 7搭建Gitlab流程
目录 1、查询docker镜像gitlab-ce 2、拉取镜像 3、查询已下载的镜像 4、新建gitlab文件夹 5、在gitlab文件夹下新建相关文件夹 6、创建运行gitlab的容器 7、查看docker容器 8、根据Linux地址访问gitlab 9、进入docker容器,设置用户名的和密码 10、登录git…...
Idea安装完成配置
目录: 环境配置Java配置Maven配置Git配置 基础设置编码级设置File Header自动生成序列化编号配置 插件安装MyBtisPlusRestfulTooklkit-fix 环境配置 Java配置 Idea右上方,找到Project Settings. 有些版本直接有,有些是在设置下的二级菜单下…...

超详细~25考研规划~感恩现在努力的你!!!
25考研规划 俄语,翻译过来叫我爱你 考试时间 第一天 8.30-11.30政治——100分 2.00-5.00英语——100分 第二天 8.30-11.30数学——150分 2.00-5.00专业课——150分 1.什么是25考研 将在2024年12月参加考研,2025年本科毕业,9月读研究…...

智慧城市安全监控的新利器
在传统的城市管理中,井盖的监控一直是一个难题,而井盖异动传感器的出现为这一问题提供了有效的解决方案。它具有体积小、重量轻、安装方便等特点,可以灵活地应用于各种类型的井盖,实现对城市基础设施的全方位监控。 智能井盖监测终…...
)
【算法】石子合并(区间dp)
题目 设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子…...

C++-特殊类和单例模式
1.请设计一个类,不能被拷贝 拷贝构造函数以及赋值运算符重载,因此想要让一个类禁止拷贝,只需让该类不能调用拷贝构造函数以及赋值运算符重载即可。 //该类不能发生拷贝class NonCopy{public:NonCopy(const NonCopy& Nc) delete;NonCopy&…...

【开源】基于Vue.js的智能教学资源库系统
项目编号: S 050 ,文末获取源码。 \color{red}{项目编号:S050,文末获取源码。} 项目编号:S050,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 课程档案模块2.3 课…...

C语言之qsort()函数的模拟实现
C语言之qsort()函数的模拟实现 文章目录 C语言之qsort()函数的模拟实现1. 简介2. 冒泡排序3. 对冒泡排序进行改造4. 改造部分4.1 保留部分的冒泡排序4.2 比较部分4.3 交换部分 5. bubble_sort2完整代码6. 使用bubble_sort2来排序整型数组7. 使用bubble_sort2来排序结构体数组7.…...

数字化未来:实时云渲染在智慧城市中的创新应用
数字中国战略"是国家推动数字经济发展的战略框架。这个战略旨在加速数字化转型,推动信息技术在各个领域的应用,提高社会经济效益和人民生活质量。而智慧城市作为其中的重要一环,重要性不言而喻。 智慧城市是当今城市发展的热点和趋势&a…...
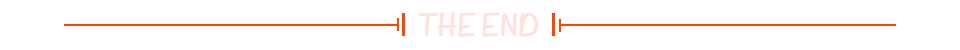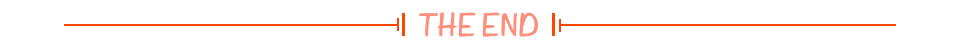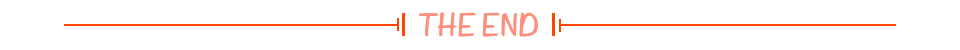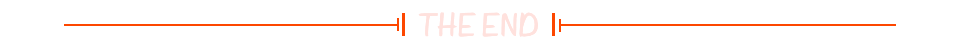
Go语言常用命令详解(二)
文章目录 前言常用命令go bug示例参数说明 go doc示例参数说明 go env示例 go fix示例 go fmt示例 go generate示例 总结写在最后 前言 接着上一篇继续介绍Go语言的常用命令 常用命令 以下是一些常用的Go命令,这些命令可以帮助您在Go开发中进行编译、测试、运行和…...

ChatGPT 从零到一打造私人智能英语学习助手
近几年,随着智能化技术的发展和人工智能的兴起,越来越多的应用程序开始涌现出来。在这些应用中,语音识别、自然语言处理以及机器翻译等技术都得到了广泛的应用。其中,聊天机器人成为了最受欢迎的人工智能应用之一,它们…...
-盛最多水的容器)
算法升级之路(七)-盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 原题链接: 盛最多水的容器 解题思路&…...

milvus数据库索引管理
一、建立向量索引 默认情况下,Milvus不会对小于1,024行的段进行索引。 1.准备索引参数 index_params {"metric_type":"L2","index_type":"IVF_FLAT","params":{"nlist":1024} } #"nlist"…...

JVM中的 -Xms参数 设置 JVM 的初始堆大小
在 Java 虚拟机(JVM)的配置中,-Xms 是一个启动参数,用于设置 JVM 的初始堆大小(Initial Heap Size)。这个参数对于优化 Java 应用程序的性能非常重要,特别是在处理需要大量内存的应用程序时。 …...
Idea 创建 Spring 项目(保姆级)
描述信息 最近卷起来,系统学习Spring;俗话说:万事开头难;创建一个Spring项目在网上找了好久没有找到好的方式;摸索了半天产出如下文档。 在 Idea 中新建项目 填写信息如下 生成项目目录结构 pom添加依赖 <depende…...
:C++11 多线程快速入门)
C++多线程学习(一):C++11 多线程快速入门
参考引用 C11 14 17 20 多线程从原理到线程池实战代码运行环境:Visual Studio 2019 1. 为什么要用多线程 任务分解 耗时的操作,任务分解,实时响应 数据分解 充分利用多核CPU处理数据 数据流分解 读写分离,解耦合设计 2. 第一个…...
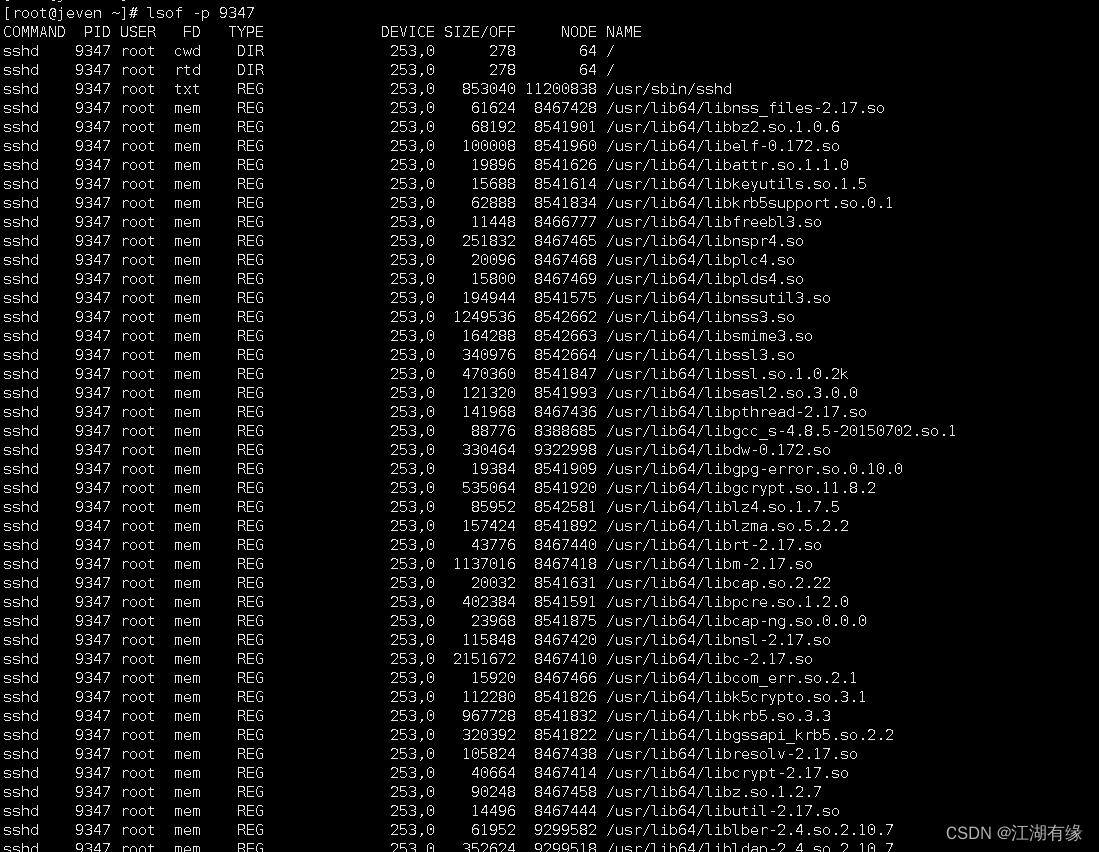
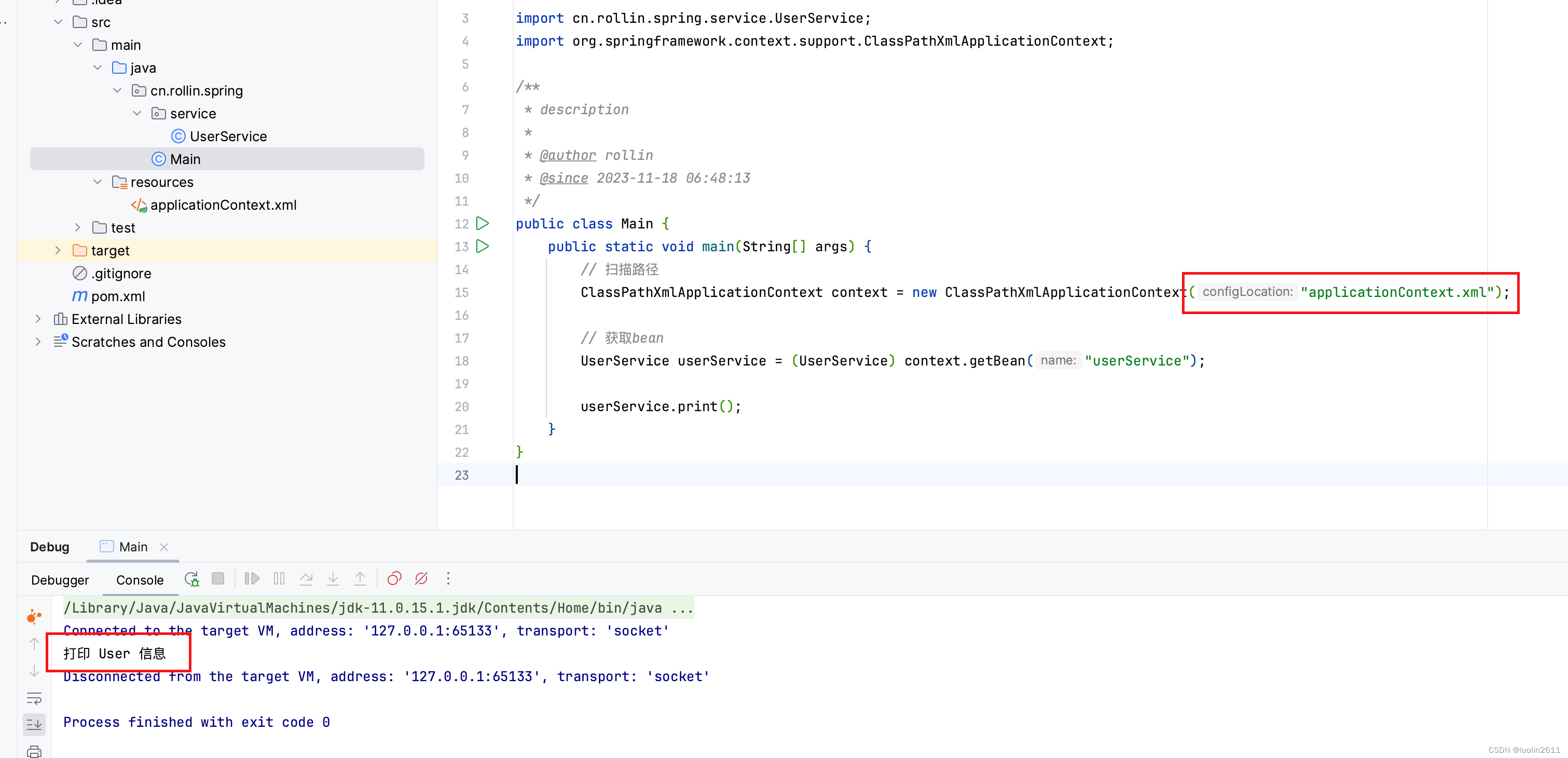
Linux系统之lsof命令的基本使用
Linux系统之lsof命令的基本使用 一、lsof命令的基本使用二、lsof命令的使用帮助2.1 lsof命令的help帮助信息2.2 lsof命令帮助解释 三、lsof的基本使用3.1 直接使用lsof命令3.2 查看某个进程打开的所有文件3.3 查看某个用户打开的所有文件3.4 查看某个文件被哪些进程打开3.5 查看…...

性能压力测试的优势与重要性
性能压力测试是软件开发过程中至关重要的一环,它通过模拟系统在极限条件下的运行,以评估系统在正常和异常负载下的表现。这种测试为确保软件系统的可靠性、稳定性和可伸缩性提供了关键信息。下面将探讨性能压力测试的优势以及为什么在软件开发中它具有不…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
