第14届蓝桥杯青少组python试题解析:23年5月省赛
选择题
T1. 执行以下代码,输出结果是()。
lst = "abc"
print(lst+lst)
- abcabc
- abc
- lst+lst
- abc+abc
T2. 执行以下代码,输出的结果是()。
age = {16,18,17}
print(type(sorted(age)))
-
<class 'set'> -
<class 'int'> -
<class 'str'> -
<class 'list'>
sorted(iterable, cmp=None, key=None, reverse=False)将返回一个新的list,不会改变原来的可迭代对象。
T3. 导入random标准库,执行print(random.randrange(2,20,2))语句,可能输出的结果是()。
- 2
- 5
- 13
- 20
random.randrange ([start,] stop [,step])
- 必须参数
stop表示随机生成的范围上限(不包括上限)start表示随机生成的范围下限(包括下限)step表示随机生成数之间的间隔,默认是1。
T4. 下列选项哪一个是转为整数的函数()?
-
str() -
int() -
float -
list()
T5. 以下关于Python中复数描述,错误的是()。
- 复数可以看作二元有序浮点数(x,y)
- 实部和虚部都是浮点数
- 虚数部分的后缀可以是"j",也可以是"J"
- 已知复数a,可以使用real获得虚数部分。
在Python中,复数类型用
complex表示。它可以通过以下方式创建:
- 直接指定实部和虚部:
complex(real, imag),real是实数部分,imag是虚数部分。- 使用字符串:
complex(string)例如:
a = complex(3, 4) # 创建一个复数3+4j a = complex('3+4j') # 创建一个复数3+4j
编程题
T1. N + N
问题描述
给定一个正整数 N N N,计算出 N + N N+N N+N的值。
例如: N = 4 N = 4 N=4, 4 + 4 4+4 4+4的值为 8 8 8。
输入描述
输入一个正整数 N N N
输出描述
输出 N + N N+N N+N的值
样例输入
4
样例输出
8
代码实现
n = int(input())
print(n + n)
T2. 字符
问题描述
给定一个只包含小写字母的字符串 S S S( S S S长度 ≥ 3 ≥3 ≥3),请输出字符串 S S S的第一个字符和最后一个字符。例如:
当S ="abc", a b c abc abc的第一个字符为 a a a,最后一个字符为 c c c,故输出 a c ac ac。
输入描述
输入一个只包含小写字母的字符串 S S S( S S S长度 ≥ 3 ≥3 ≥3)。
输出描述
输出字符串 S S S的第一个字符和最后一个字符,两个字符之间没有空格及其他字符
样例输入
abc
样例输出
ac
代码实现
s = input()
print(s[0] + s[-1])
T3. 数字币
问题描述
提示信息:合数指自然数中除了能被1和本身整除外,还能被其它正整数整除的数。例如 4 4 4, 4 4 4除了能被 1 1 1和 4 4 4整除,还可以被 2 2 2整除。
小明收藏了 N N N( 2 ≤ N ≤ 25 2≤N≤25 2≤N≤25)个数字币,每个数字币上都有一个面值(面值可以重复)。从数字币中任选 K K K( 2 ≤ K ≤ N 2≤K≤N 2≤K≤N)个,有多种选法,请将每次选择的数字币上的面值累加,然后解决以下两个问题:
- 问题1:累加的和中有多少种不同的结果
- 问题2:累加的和中有多少个不同的合数
例如: N = 5 N=5 N=5, K = 3 K=3 K=3, 5 5 5个数字币上的面值分别为 2 、 1 、 4 、 5 、 3 2、1、4、5、3 2、1、4、5、3,任选 3 3 3个数字币,有 10 10 10种选法,将每种选法上的面值累加: 2 + 1 + 4 = 7 、 2 + 1 + 5 = 8 、 2 + 1 + 3 = 6 、 2 + 4 + 5 = 11 、 2 + 4 + 3 = 9 、 2 + 5 + 3 = 10 、 1 + 4 + 5 = 10 、 1 + 4 + 3 = 8 、 1 + 5 + 3 = 9 、 4 + 5 + 3 = 12 2+1+4=7、2+1+5=8、2+1+3=6、2+4+5=11、2+4+3=9、2+5+3=10、1+4+5=10、1+4+3=8、1+5+3=9、4+5+3=12 2+1+4=7、2+1+5=8、2+1+3=6、2+4+5=11、2+4+3=9、2+5+3=10、1+4+5=10、1+4+3=8、1+5+3=9、4+5+3=12
其中累加的和中有 7 7 7种不同的结果,分别是 7 、 8 、 6 、 11 、 9 、 10 、 12 7、8、6、11、9、10、12 7、8、6、11、9、10、12;累加的和中有 5 5 5个不同的合数,分别是 8 、 6 、 9 、 10 、 12 8、6、9、10、12 8、6、9、10、12。
输入描述
第一行输入一个正整数 N N N( 2 ≤ N ≤ 25 2≤N≤25 2≤N≤25),表示数字币的个数。
第二行输入 N N N个正整数( 1 ≤ 1≤ 1≤正整数 ≤ 1000 ≤1000 ≤1000),表示数字币上的面值,正整数之间以一个英文逗号隔开。
第三行输入一个正整数 K K K( 2 ≤ K ≤ N 2≤K≤N 2≤K≤N),表示所要选取的数字币个数。
输出描述
输出两个整数,分别表示累加的和中不同结果的个数以及累加的结果中不同合数的个数,两个整数之间以一个英文逗号隔开。
样例输入
5
2,1,4,5,3
3
样例输出
7,5
代码实现
n = int(input())
a = eval(input())
k = int(input())
d = {}
ans1, ans2 = 0, 0
b = [0] * n
# 检查x是否为合数
def check(x):i = 2while i * i <= x:if x % i == 0:return Truei += 1return False
def dfs(t, last, s):if t == k:global ans1, ans2# 如果字典中不存在sif s not in d:d[s] = 1ans1 += 1# 检查是否为合数if check(s):ans2 += 1return;for i in range(last + 1, n):dfs(t + 1, i, s + a[i])
dfs(0, -1, 0)
print('%d,%d' % (ans1, ans2))
T4. 杨辉三角
问题描述
提示信息:杨辉三角就是一个用数排列起来的三角形(如下图),杨辉三角规则如下:
- 每行第一个数和最后一个数都为 1 1 1,其它每个数等于它左上方和右上方的两数之和;
- 第 n n n行有 n n n个数。
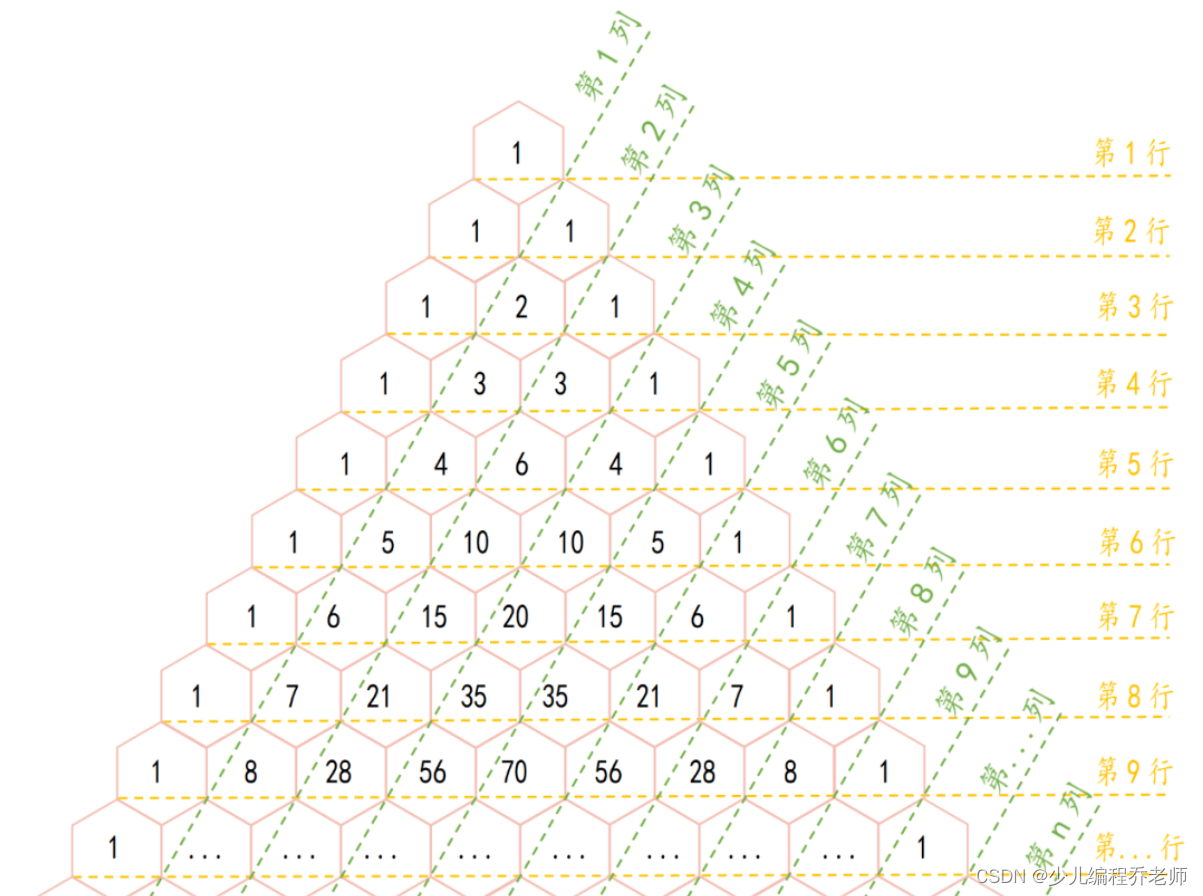
注意:“列”指的是如图所标注的斜列。
小青对杨辉三角的特点和规律研究得很明白,现要考察你对杨辉三角的熟悉程度,首先告知你这是一个 N N N行的杨辉三角,然后又告知了两个数值 X X X和 Y Y Y( X X X表示第几行, Y Y Y表示第几列),让你根据杨辉三角的特点和观察到的规律解决以下两个问题。
- 第 X X X行第 Y Y Y列对应的数是多少;
- 求出 N N N行的杨辉三角中第 Y Y Y列中所有数的和。
例如: N = 5 N=5 N=5, 5 5 5行的杨辉三角如下图。
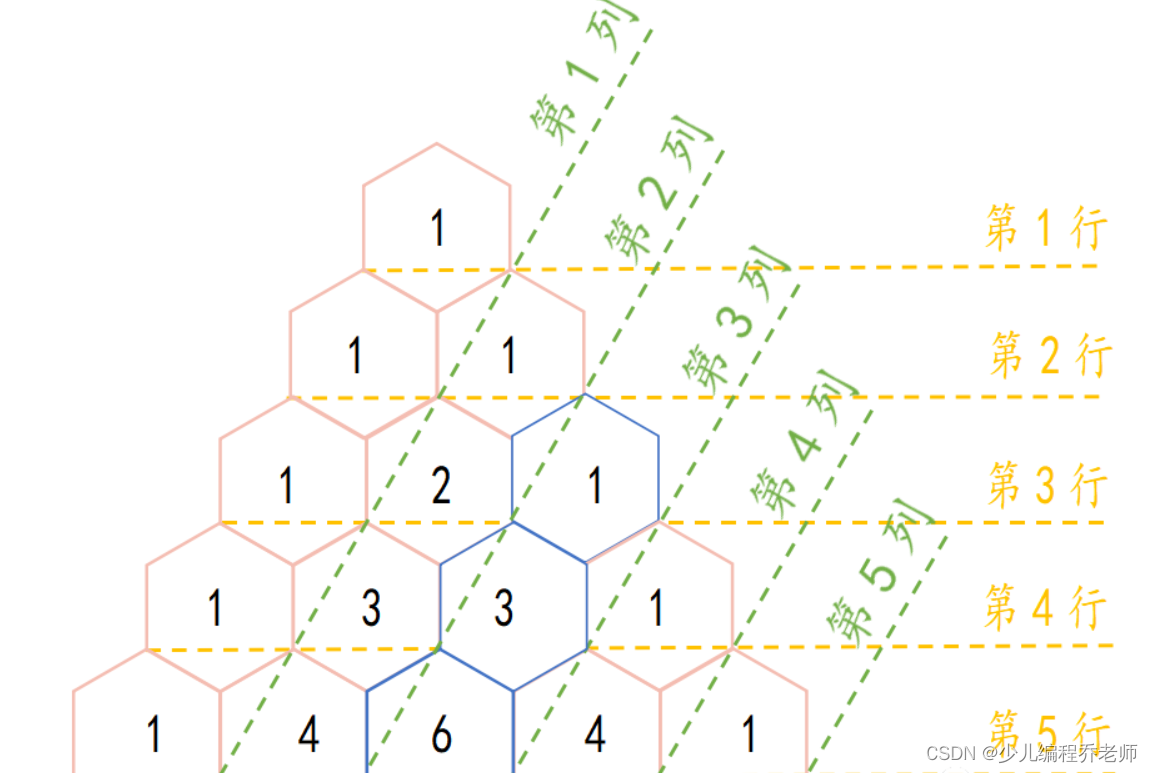
X = 5 X=5 X=5, Y = 3 Y=3 Y=3,第 5 5 5行第 3 3 3列对应的数为 6 6 6;第 3 3 3列中所有数的和为 10 10 10( 10 = 6 + 3 + 1 10 = 6 + 3 + 1 10=6+3+1)。
输入描述
第一行输入一个正整数 N N N( 2 ≤ N ≤ 30 2≤N≤30 2≤N≤30),表示杨辉三角的行数
第二行输入两个正整数 X X X和 Y Y Y( 1 ≤ Y ≤ X ≤ N 1≤Y≤X≤N 1≤Y≤X≤N),分别表示第 X X X行和第 Y Y Y列,正整数之间以一个英文逗号隔开。
输出描述
输出两个整数,分别表示 N N N行的杨辉三角中第 X X X行 Y Y Y列对应的数,及第 Y Y Y列上所有数的和,两个整数之间以一个英文逗号隔开。
样例输入
5
5,3
样例输出
6,10
代码实现
n = int(input())
x, y = eval(input())
# 初始化二维列表
f = [[0] * (n + 1) for _ in range(n + 1)]
# 计算杨辉三角,行列的下标从1开始
for i in range(1, n + 1):for j in range(1, i + 1):if i == 1 or j == i:f[i][j] = 1else:f[i][j] = f[i - 1][j] + f[i - 1][j - 1]
ans1 = f[x][y]
ans2 = 0
for i in range(1, n + 1):ans2 += f[i][y];
print('%d,%d' % (ans1, ans2))
T5. 涂鸦
问题描述
工人砌了一面奇特的砖墙,该墙由 N N N列砖组成( 1 ≤ N ≤ 1 0 6 1≤N≤10^6 1≤N≤106),且每列砖的数量为 K i K_i Ki( 1 ≤ K i ≤ 1 0 4 1≤K_i≤10^4 1≤Ki≤104,相邻两列砖之间无缝隙),每块砖的长宽高都为 1 1 1。
小蓝为了美化这面墙,需要在这面墙中找到一块面积最大的矩形用于涂鸦,那么请你帮助小蓝找出最大矩形,并输出其面积。
例如: N = 6 N = 6 N=6,表示这面墙有 6 6 6列,每列砖的数量依次为 3 、 2 、 1 、 5 、 6 、 2 3、2、1、5、6、2 3、2、1、5、6、2,如下图:
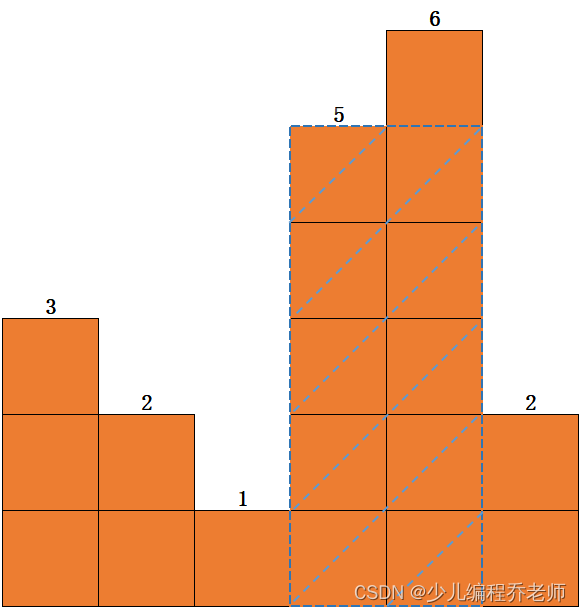
图中虚线部分是一块面积最大的矩形,其面积为 10 10 10。
输入描述
第一行输入一个正整数 N N N( 1 ≤ N ≤ 1 0 6 1≤N≤10^6 1≤N≤106),表示这面砖墙由几列砖组成
第二行输入 N N N个正整数 K i K_i Ki( 1 ≤ K i ≤ 1 0 4 1≤K_i≤10^4 1≤Ki≤104),表示每列砖的数量,正整数之间以一个空格隔开。
输出描述
输出一个正整数,表示最大矩形的面积。
样例输入
6
3 2 1 5 6 2
样例输出
10
算法思想1(60分,暴力枚举)
矩形的面积等于列数 × \times ×相邻列的高度最小值。因此可以暴力枚举所有相邻列的组合,计算其面积,然后打擂台求最大值即可。
时间复杂度
尝试所有相邻列的组合需要分别枚举开始列和结束列,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
代码实现
n = int(input())
a = list(map(int, input().split()))
ans = 0
# 枚举矩形的开始列
for i in range(n):# 枚举矩形的结束列for j in range(i, n):# 从i到j一共有j - i + 1列,这些列中高度的最小值为min(a[i : j + 1]ans = max(ans, (j - i + 1) * min(a[i : j + 1]))
print(ans)
算法思想2(100分,枚举 + 单调栈)
矩形的面积等于每列砖的数量 × \times × 与它左右相邻的且具有相同高度的列数。因此可以枚举每列砖的数量,第 i i i列来说,不妨设其砖的数量为 a i a_i ai:
- 向左找到第一个小于 a i a_i ai的位置 L i L_i Li
- 向右找到第一个小于 a i a_i ai的位置 R i R_i Ri
此时以第 i i i列砖为高度的矩形的面积 = ( R i − L i − 1 ) × a i =(R_i - L_i-1)\times a_i =(Ri−Li−1)×ai,那么只需要打擂台求最大值即可。
那么如何向左(向右)找到第一个小于 a i a_i ai的位置呢,可以使用单调栈的思想,以 O ( 1 ) O(1) O(1)的时间复杂度实现。
时间复杂度
- 枚举每列砖的时间复杂度为 O ( n ) O(n) O(n)
- 单调栈向左(向右)找到第一个小于 a i a_i ai的位置的时间复杂度为 O ( 1 ) O(1) O(1)
总的时间复杂度为 O ( n ) O(n) O(n)。
代码实现
n = int(input())
a = list(map(int, input().split()))
L = [0] * n
R = [0] * n
# 单调栈查找左侧第一个小于a[i]的位置L[i]
stk = []
for i in range(n):while len(stk) != 0 and a[stk[-1]] >= a[i]:stk.pop()if len(stk) == 0: # 左侧没有比a[i]小的数L[i] = -1else:L[i] = stk[-1] # 栈顶就是左侧第一个比a[i]小的位置stk.append(i)
# 单调栈查找右侧第一个小于a[i]的位置R[i]
stk = []
for i in range(n - 1, -1, -1):while len(stk) != 0 and a[stk[-1]] >= a[i]:stk.pop()if len(stk) == 0: #右侧没有比a[i]小的数R[i] = nelse:R[i] = stk[-1] # 栈顶就是右侧第一个比a[i]小的位置stk.append(i)
ans = 0
for i in range(n):# (L, R)之间一共有R - L - 1列ans = max(ans, a[i] * (R[i] - L[i] - 1))
print(ans)T6. 传送门(仅中、高级组)
问题描述
在一个神奇空间里有 N N N个房间,房间从 1 1 1到 N N N编号,每个房间可能有一个或多个传送门,每个传送门都有一个编号,如果相同编号的传送门同时出现在多个房间中,表示这些房间可以互通。
给定两个房间的编号 A A A和 B B B,请找出从房间 A A A到达房间 B B B最少需要经过几个传送门。
例如: N = 3 N=3 N=3, 3 3 3个房间中传送门的编号分别为:
房间 1 1 1: 1 , 4 , 6 1,4,6 1,4,6;
房间 2 2 2: 2 , 3 , 4 , 8 2,3,4,8 2,3,4,8;
房间 3 3 3: 3 , 6 , 9 3,6,9 3,6,9。
其中房间 1 1 1和房间 2 2 2互通,共用 4 4 4号传送门;房间 1 1 1和房间 3 3 3互通,共用 6 6 6号传送门;房间 2 2 2和房间 3 3 3互通,共用 3 3 3号传送门;当 A = 1 A=1 A=1, B = 2 B=2 B=2,从房间 1 1 1到达房间 2 2 2,共有两种路线:
- 路线 1 1 1:从房间 1 1 1通过 4 4 4号传送门进入房间 2 2 2,共经过 1 1 1个传送门。如下图橙色路线所示。
- 路线 2 2 2:从房间 1 1 1通过 6 6 6号传送门进入房间 3 3 3,再从房间 3 3 3通过 3 3 3号传送门进入房间 2 2 2,共经过 2 2 2个传送门;故从房间 1 1 1到达房间 2 2 2最少需要经过 1 1 1个传送门。如下图黑色路线所示。

输入描述
第一行输入一个正整数 N N N( 2 ≤ N ≤ 20 2≤N≤20 2≤N≤20),表示房间数量。
接下来输入 N N N行,每行包含多个正整数( 1 ≤ 1≤ 1≤正整数 ≤ 100 ≤100 ≤100),第 2 2 2行到第 N + 1 N+1 N+1行依次表示 1 1 1到 N N N号房间内所有传送门的编号,正整数之间以一个英文逗号隔开。
最后一行输入两个正整数 A A A和 B B B( 1 ≤ A ≤ N , 1 ≤ B ≤ N 1≤A≤N,1≤B≤N 1≤A≤N,1≤B≤N,且 A ≠ B A≠B A=B),表示两个房间的编号,正整数之间以一个英文逗号隔开。
输出描述
输出一个整数,表示从房间 A A A到达房间 B B B最少需要经过几个传送门,如果房间 A A A不能到达房间 B B B,则输出 − 1 -1 −1
样例输入
3
1,4,6
2,3,4,8
3,6,9
1,2
样例输出
1
算法思想
- 首先,输入每个房间的传送门编号,可以计算出任意两个房间是否有传送门相连
- 然后,可以通过BFS求到起点 A A A的最短路径。
代码实现
n = int(input())
a = []
for i in range(n):b = eval(input())a.append(b)
A, B = eval(input())# g数组存储两个房间是否有传送门
g = [[0] * n for _ in range(n)]for i in range(n):for j in range(i + 1, n):for x in a[i]:if x in a[j]:# 第i个房间和第j个房间有传送门g[i][j] = g[j][i] = 1break
# bfs求最短路
ans = 0
st = [0] * n
q = [] # 队列
q.append((A, 0)) # 将起点和到起点的距离入队
st[A] = 1 # 将起点标记为已访问
# 只要队列不空,bfs计算到起点的最短路径
while len(q) != 0:x, d = q.pop(0)if(x == B): # 如果到达终点ans = dbreakfor i in range(n):# 如果i点已访问,或者x到i之间没有传送门if st[i] == 1 or g[x][i] == 0:continueq.append((i, d + 1))
print(ans)相关文章:

第14届蓝桥杯青少组python试题解析:23年5月省赛
选择题 T1. 执行以下代码,输出结果是()。 lst "abc" print(lstlst)abcabc abc lstlst abcabc T2. 执行以下代码,输出的结果是()。 age {16,18,17} print(type(sorted(age)))<class set&…...
SpringCloud 微服务全栈体系(十四)
第十一章 分布式搜索引擎 elasticsearch 四、RestAPI ES 官方提供了各种不同语言的客户端,用来操作 ES。这些客户端的本质就是组装 DSL 语句,通过 http 请求发送给 ES。官方文档地址:https://www.elastic.co/guide/en/elasticsearch/client/…...

【开题报告】基于微信小程序的个人健康管理系统的设计与实现
1.选题背景与意义 在现代社会,人们对健康的关注日益增加。随着生活方式的变化和工作压力的增加,许多人意识到保持良好的身体健康对于提高生活质量和幸福感的重要性。 然而,许多人在日常生活中缺乏对自身健康状况的了解和管理。他们可能没有…...

Swagger笔记
一、导包 <!--引入swagger--> <dependency><groupId>io.springfox</groupId><artifactId>springfox-swagger2</artifactId><version>2.9.2</version> </dependency> <!--前端的UI界面--> <dependency><…...
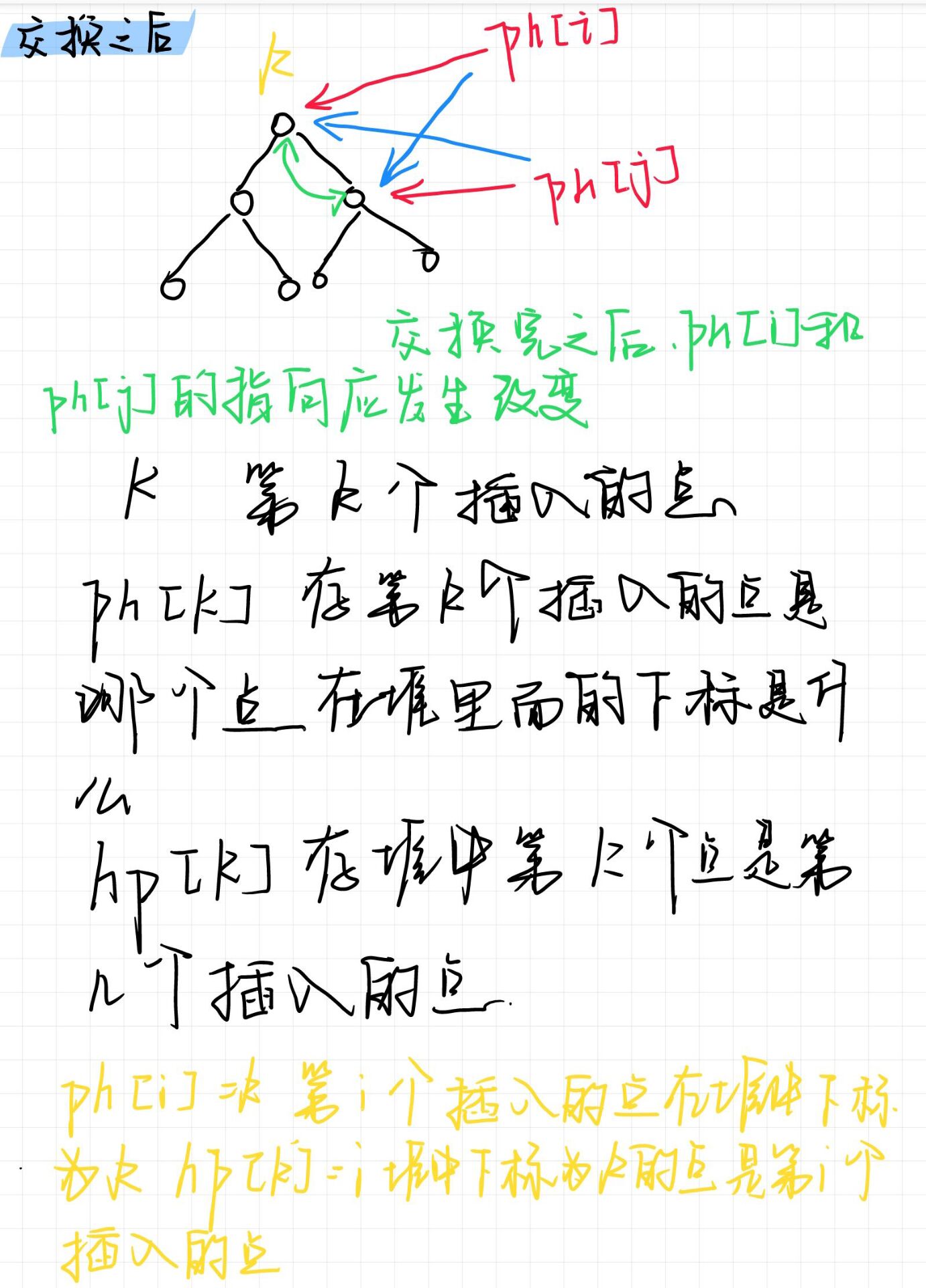
数据结构 堆
手写堆,而非stl中的堆 如何手写一个堆? //将数组建成堆 <O(n) for (int i n / 2;i;i--) //从n/2开始down down(i); 从n/2元素开始down,最下面一层元素的个数是n/2,其余上面的元素的个数是n/2,从最下面一层到最高层…...
将 ONLYOFFICE 文档编辑器与 Node.js 应用集成
我们来了解下,如何将 ONLYOFFICE 文档编辑器与您的 Web 应用集成。 许多 Web 应用都可以从文档编辑功能中获益。但是要从头开始创建这个功能,需要花费大量时间和精力。幸运的是,您可以使用 ONLYOFFICE——这是一款开源办公套件,可…...
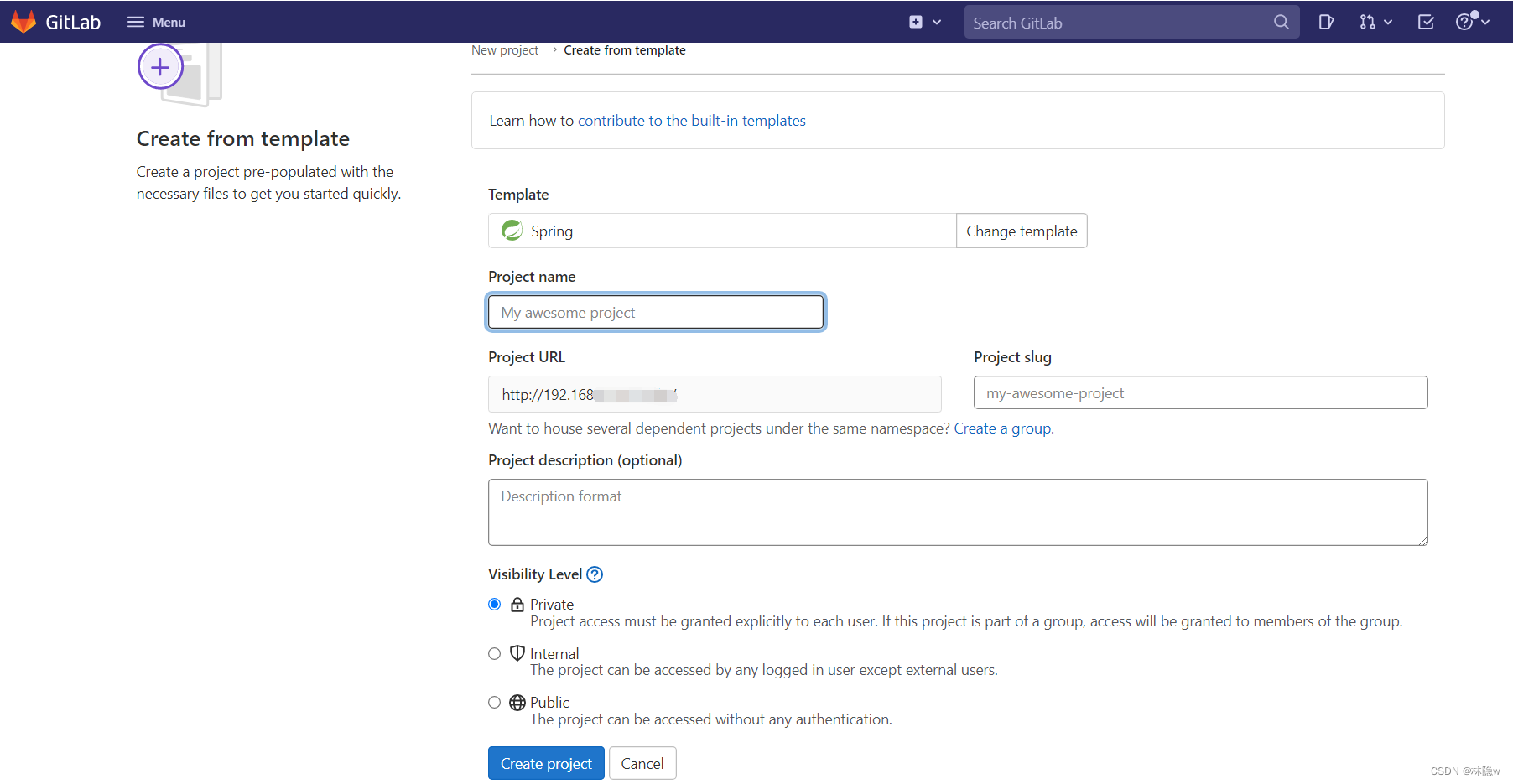
CentOS 7搭建Gitlab流程
目录 1、查询docker镜像gitlab-ce 2、拉取镜像 3、查询已下载的镜像 4、新建gitlab文件夹 5、在gitlab文件夹下新建相关文件夹 6、创建运行gitlab的容器 7、查看docker容器 8、根据Linux地址访问gitlab 9、进入docker容器,设置用户名的和密码 10、登录git…...
Idea安装完成配置
目录: 环境配置Java配置Maven配置Git配置 基础设置编码级设置File Header自动生成序列化编号配置 插件安装MyBtisPlusRestfulTooklkit-fix 环境配置 Java配置 Idea右上方,找到Project Settings. 有些版本直接有,有些是在设置下的二级菜单下…...

超详细~25考研规划~感恩现在努力的你!!!
25考研规划 俄语,翻译过来叫我爱你 考试时间 第一天 8.30-11.30政治——100分 2.00-5.00英语——100分 第二天 8.30-11.30数学——150分 2.00-5.00专业课——150分 1.什么是25考研 将在2024年12月参加考研,2025年本科毕业,9月读研究…...

智慧城市安全监控的新利器
在传统的城市管理中,井盖的监控一直是一个难题,而井盖异动传感器的出现为这一问题提供了有效的解决方案。它具有体积小、重量轻、安装方便等特点,可以灵活地应用于各种类型的井盖,实现对城市基础设施的全方位监控。 智能井盖监测终…...
)
【算法】石子合并(区间dp)
题目 设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子…...

C++-特殊类和单例模式
1.请设计一个类,不能被拷贝 拷贝构造函数以及赋值运算符重载,因此想要让一个类禁止拷贝,只需让该类不能调用拷贝构造函数以及赋值运算符重载即可。 //该类不能发生拷贝class NonCopy{public:NonCopy(const NonCopy& Nc) delete;NonCopy&…...

【开源】基于Vue.js的智能教学资源库系统
项目编号: S 050 ,文末获取源码。 \color{red}{项目编号:S050,文末获取源码。} 项目编号:S050,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 课程档案模块2.3 课…...

C语言之qsort()函数的模拟实现
C语言之qsort()函数的模拟实现 文章目录 C语言之qsort()函数的模拟实现1. 简介2. 冒泡排序3. 对冒泡排序进行改造4. 改造部分4.1 保留部分的冒泡排序4.2 比较部分4.3 交换部分 5. bubble_sort2完整代码6. 使用bubble_sort2来排序整型数组7. 使用bubble_sort2来排序结构体数组7.…...

数字化未来:实时云渲染在智慧城市中的创新应用
数字中国战略"是国家推动数字经济发展的战略框架。这个战略旨在加速数字化转型,推动信息技术在各个领域的应用,提高社会经济效益和人民生活质量。而智慧城市作为其中的重要一环,重要性不言而喻。 智慧城市是当今城市发展的热点和趋势&a…...
Go语言常用命令详解(二)
文章目录 前言常用命令go bug示例参数说明 go doc示例参数说明 go env示例 go fix示例 go fmt示例 go generate示例 总结写在最后 前言 接着上一篇继续介绍Go语言的常用命令 常用命令 以下是一些常用的Go命令,这些命令可以帮助您在Go开发中进行编译、测试、运行和…...

ChatGPT 从零到一打造私人智能英语学习助手
近几年,随着智能化技术的发展和人工智能的兴起,越来越多的应用程序开始涌现出来。在这些应用中,语音识别、自然语言处理以及机器翻译等技术都得到了广泛的应用。其中,聊天机器人成为了最受欢迎的人工智能应用之一,它们…...
-盛最多水的容器)
算法升级之路(七)-盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 原题链接: 盛最多水的容器 解题思路&…...

milvus数据库索引管理
一、建立向量索引 默认情况下,Milvus不会对小于1,024行的段进行索引。 1.准备索引参数 index_params {"metric_type":"L2","index_type":"IVF_FLAT","params":{"nlist":1024} } #"nlist"…...

JVM中的 -Xms参数 设置 JVM 的初始堆大小
在 Java 虚拟机(JVM)的配置中,-Xms 是一个启动参数,用于设置 JVM 的初始堆大小(Initial Heap Size)。这个参数对于优化 Java 应用程序的性能非常重要,特别是在处理需要大量内存的应用程序时。 …...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
