最大子段和(分治法+动态规划法)
求最大子段和
此类问题通常是求数列中连续子段和的最大值,经典的股票问题就是考察的这个思想及拓展。
例题:
AcWing:1054. 股票买卖
Leetcode:53. 最大子数组和
分治法O(nlogn)
此类问题时分适合采用分治思想,因为所有子区间 [ s t a r t , e n d ] [start, end] [start,end]只可能有以下三种可能:
- 在 [ 1 , n 2 ] [1,\frac{n}{2}] [1,2n]这个区域内。
- 在 [ n 2 + 1 , n ] [\frac{n}{2}+1, n] [2n+1,n]这个区域内。
- 左边界位于 [ 1 , n 2 ] [1,\frac{n}{2}] [1,2n],右边界位于 [ n 2 + 1 , n ] [\frac{n}{2}+1 ,n] [2n+1,n]内。

这三种情况的最大值即为所求。前两种情况符合子问题递归特性,可以通过递归求出。
在第三种情况中 n 2 , n 2 + 1 \frac{n}{2},\frac{n}{2}+1 2n,2n+1必然包含在内,因此可以利用第二种穷举的思路分别向左右扩张求出。
int maxx = -INF;
int maxInterval(vector<int> a, int l, int r) {if(l == r) {return (a[l] > maxx) ? a[l] : maxx;}int sum_l = 0, sum_r = 0;int mid = (l + r) >> 1;sum_l = maxInterval(a, l, mid);sum_r = maxInterval(a, mid + 1, r);int s1 = 0, x = 0;for(int i = mid; i >= 0; i -- ) {x += a[i];if(x > s1) s1 = x;}int s2 = 0, y = 0;for(int i = mid + 1; i <= r; i ++ ) {y += a[i];if(y > s2) s2 = y;}maxx = max(sum_l, s1 + s2);maxx = max(maxx, sum_r);return maxx;
}
动态规划思路O(n)
如果我们用常规思路来枚举所有数字,并判断当前数字是否应该加入到最大子段;那么会发现,当前数字的选择与否并不是由前面已经遍历过的数字所决定,而是由其后面的数字来决定,这也就导致了问题的有后效性。
当出现有后效性问题时,我们当前对子问题做出的选择就不一定为最优解,因为会受到后续数据的影响。
后效性问题是动态规划中一个非常重要的概念,在此引用《算法竞赛进阶指南》(李煜东著)中的一段话:
为了保证计算子问题能够按照顺序、不重复地进行,动态规划要求已经求解的子问题不受后续阶段的影响。这个条件也被叫做无后效性。换言之,动态规划对状态空间的遍历构成一张有向无环图,遍历就是该有向无环图的一个拓扑序。有向无环图中的节点对应问题中的状态,图中的边则对应状态之间的转移,转移的选取就是动态规划中的决策。
在此问题中,我们需要换一种思路来避免有后效性问题,我们可以将遍历到的数字看作必选项,然后判断是否要加上前面的和。我们考虑使用dp[i]来表示以a[i]来结尾的子数组的最大子段和,那么我们可以得到状态转移方程为:
d p [ i ] = m a x ( a [ i ] , d p [ i − 1 ] + a [ i ] ) dp[i] = max(a[i], dp[i - 1] + a[i]) dp[i]=max(a[i],dp[i−1]+a[i])
那么结果即为: r e s = m a x ( r e s , d p [ i ] ) res=max(res, dp[i]) res=max(res,dp[i]).
int MaxInterval(vector<int> a, int len) {vector<int> dp(len);int res = -INF;dp[0] = a[0];for(int i = 1; i < len; i ++ ) {dp[i] = max(a[i], dp[i - 1] + a[i]);res = max(res, dp[i]);}return res;
}
扫描法O(n)
动态规划思路的一个空间优化版本。
由于只和当前元素前面的最大值有关,因此只需要记录前面最大值即可。
前面的最大值表示前 i − 1 i-1 i−1个问题的最优解。
int maxInterval(vector<int> v, int len) {int res = v[0], mi = min(0, v[0]), sum = v[0];for(int i = 1; i < len; i ++ ) {sum += v[i];res = max(res, sum - mi);mi = min(mi, sum);}return res;
}
相关文章:

最大子段和(分治法+动态规划法)
求最大子段和 此类问题通常是求数列中连续子段和的最大值,经典的股票问题就是考察的这个思想及拓展。 例题: AcWing:1054. 股票买卖 Leetcode:53. 最大子数组和 分治法O(nlogn) 此类问题时分适合采用分治思想,因为所有子区间 [ s t a r t …...
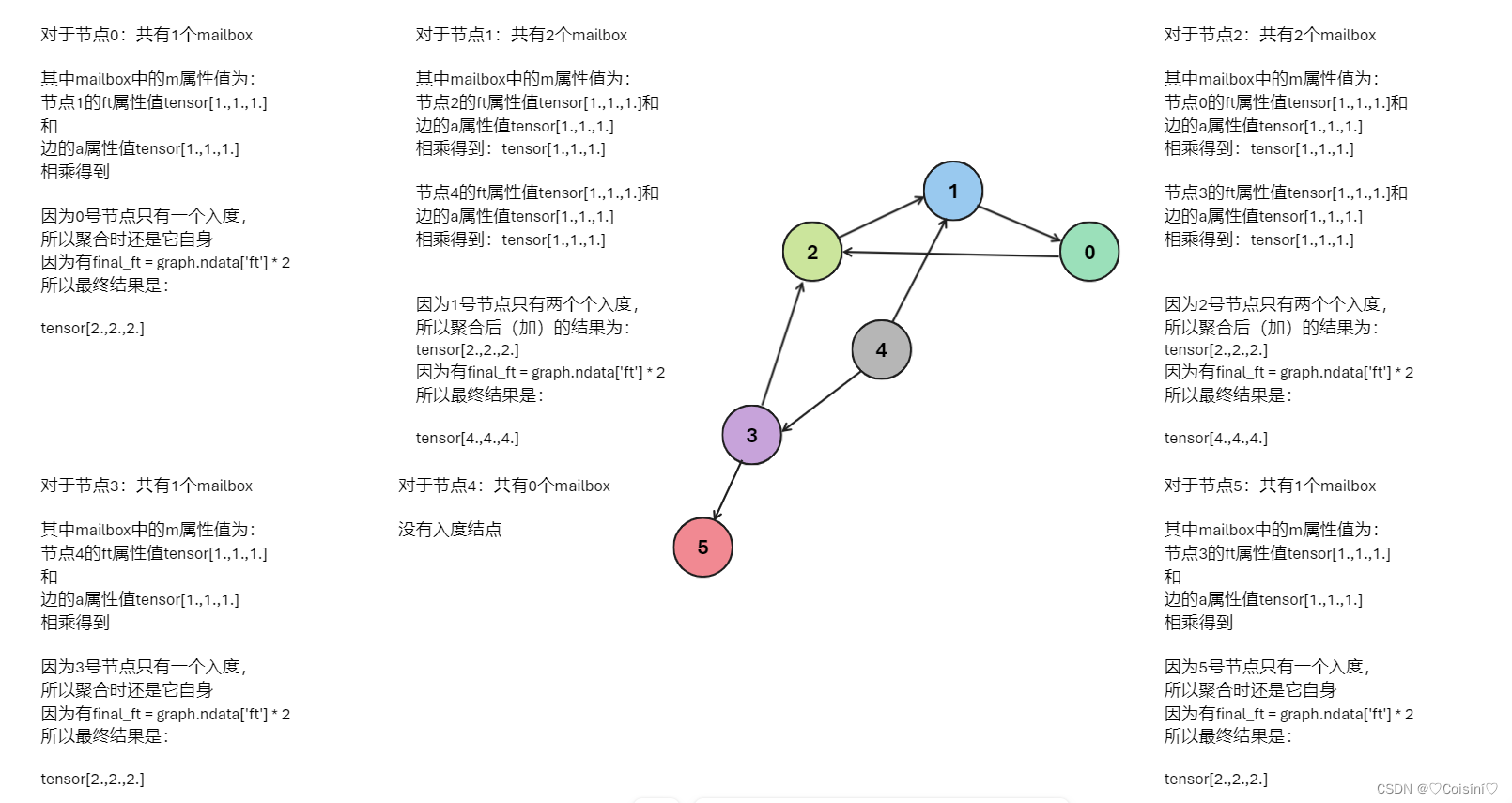
内置函数和消息传递API
消息传递范式 消息函数、聚合函数与更新函数 消息函数接受一个参数 edges,这是一个 EdgeBatch 的实例, 在消息传递时,它被DGL在内部生成以表示一批边。edges 有 src、 dst 和 data 共3个成员属性, 分别用于访问源节点、目标节点…...

不标年份的葡萄酒质量好吗?
我们在葡萄酒标上经常看到生产年份,也就是指全部葡萄采摘的年份。旧世界葡萄酒产国认为葡萄酒年份对他们的影响较大,而新世界葡萄酒,年份的意义就稍微小些。甚至有一部分葡萄酒酒标上没有年份。在酒标上没有标注年份的葡萄酒,被称…...
2023年【高处安装、维护、拆除】模拟考试题及高处安装、维护、拆除模拟考试题库
题库来源:安全生产模拟考试一点通公众号小程序 2023年【高处安装、维护、拆除】模拟考试题及高处安装、维护、拆除模拟考试题库,包含高处安装、维护、拆除模拟考试题答案和解析及高处安装、维护、拆除模拟考试题库练习。安全生产模拟考试一点通结合国家…...

简单模拟 Spring 创建的动态代理类(解释一种@Transactional事务失效的场景)
模拟 Spring 创建的动态代理类 本文主要目的是从父类和子类继承的角度去分析为什么在 Service 标注的业务类中使用 this 调用方法会造成事务失效。解释在这种情况下 this 为什么是原始类对象而不是代理类对象。 问题描述 在 Service 标注的业务类中,如果调用本类…...
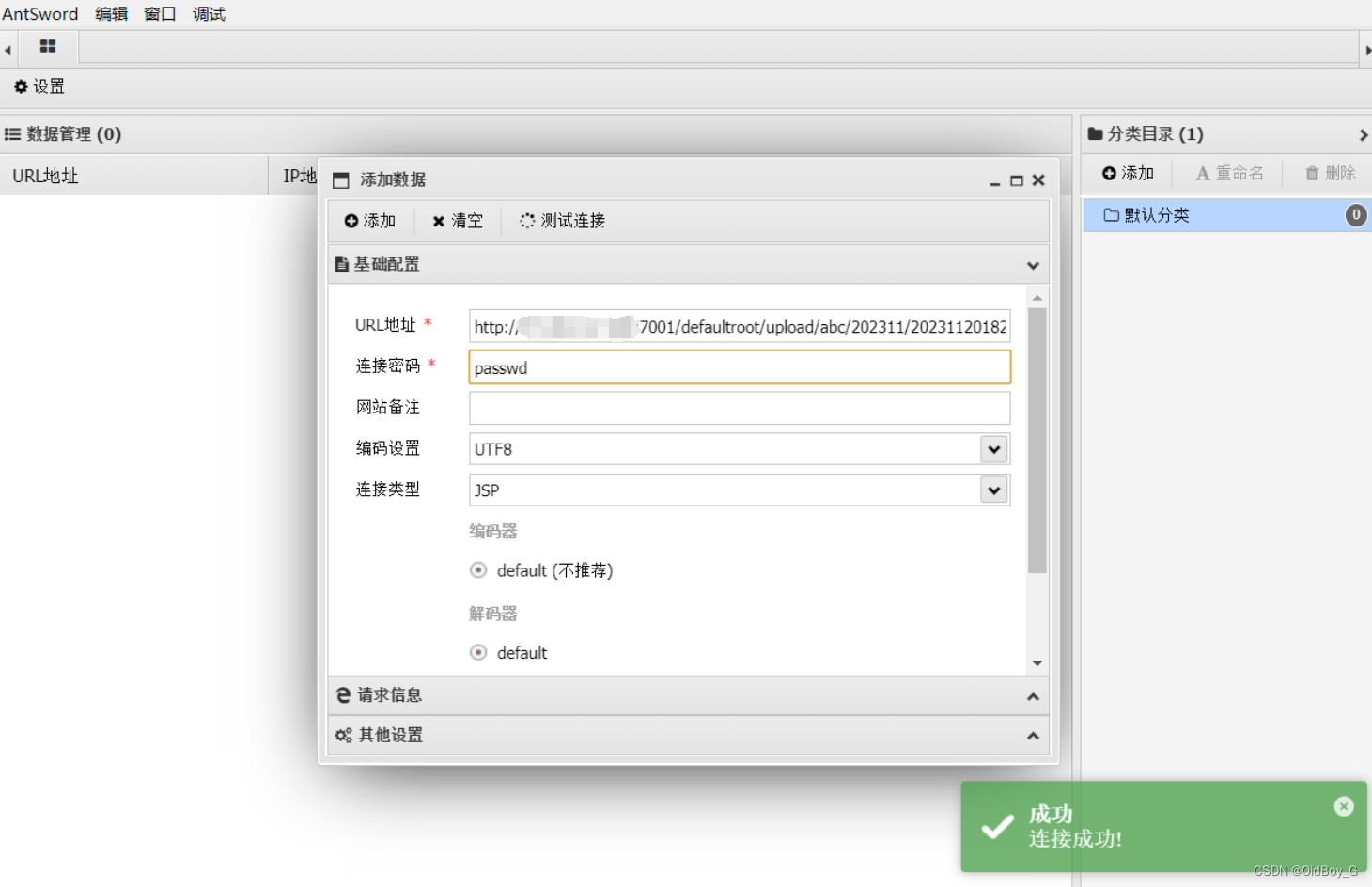
万户OA upload任意文件上传漏洞复现
0x01 产品简介 万户OA ezoffice是万户网络协同办公产品多年来一直将主要精力致力于中高端市场的一款OA协同办公软件产品,统一的基础管理平台,实现用户数据统一管理、权限统一分配、身份统一认证。统一规划门户网站群和协同办公平台,将外网信息…...

如何写好一篇软文?怎样写软文比较有吸引力?
软文,即柔性广告,是一种通过文字、图片等形式,将广告信息融入到内容中,以达到宣传、推广、营销目的的文章。企业和品牌每天都会在互联网上投放大量软文,软文起到润物细无声的作用,可以在无形中影响用户心智…...

从0开始学习JavaScript--JavaScript中的对象
JavaScript中的对象是一种重要的数据结构,它不仅是语言的基石,还提供了丰富的功能和灵活性。本文将深入研究JavaScript对象的创建、属性访问、方法定义,以及实际应用中的技巧,通过丰富的示例代码,帮助读者更全面地了解…...
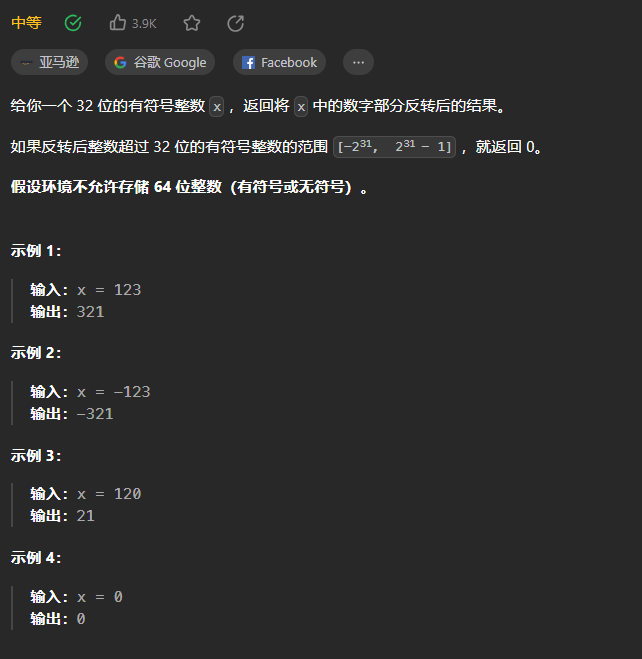
【LeetCode刷题】--7.整数反转
7.整数反转 注意:在推入数字之前,需要判断MIN_VALUE< res*10digit<MAX_VALUE,不满足就返回0 class Solution {public int reverse(int x) {int res 0;while(x!0){//需要判断MIN_VALUE< res*10digit<MAX_VALUEif(res < Integ…...
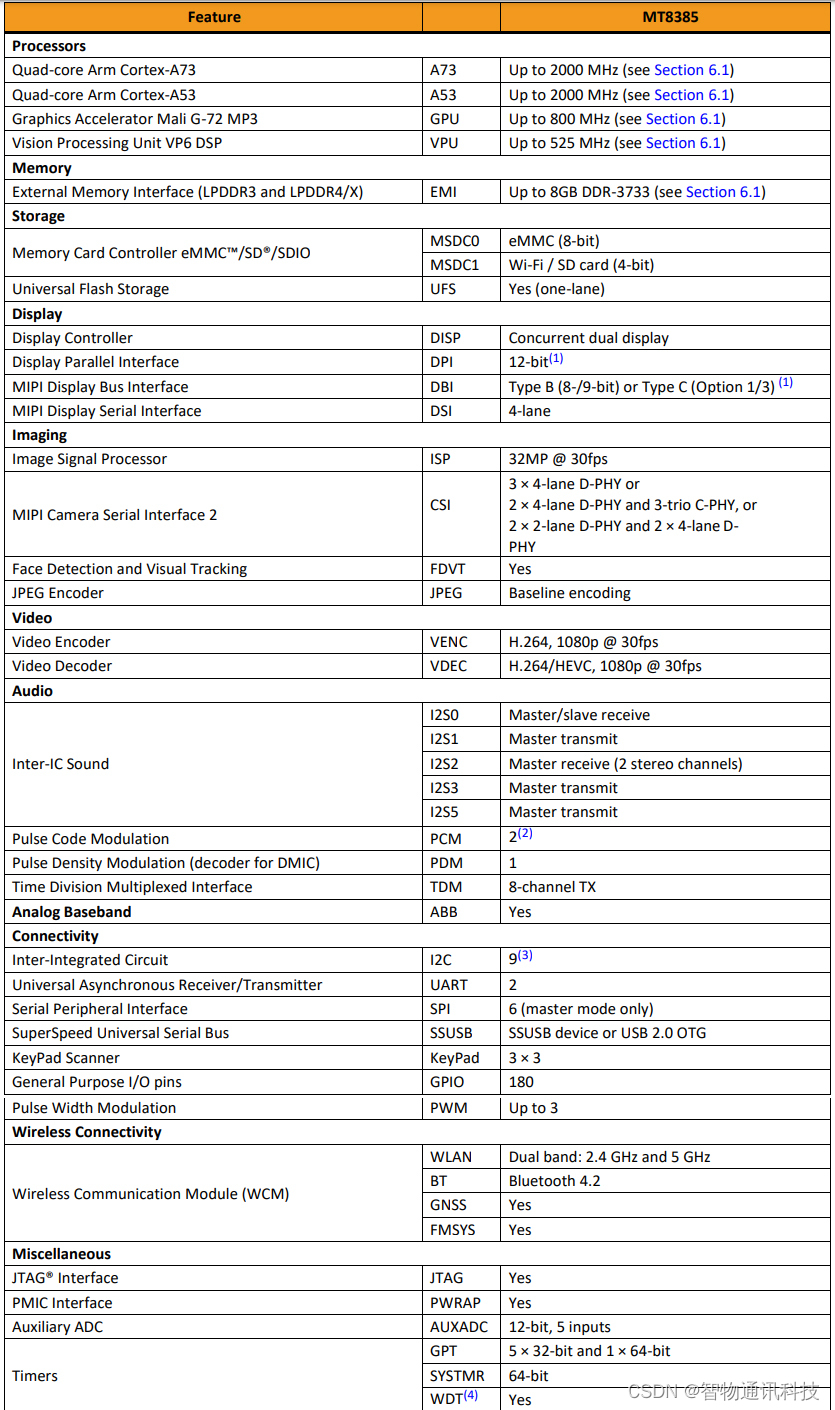
Genio 500_MT8385安卓核心板:功能强大且高效
Genio 500(MT8385)安卓核心板是一款功能强大且高效的AIoT平台,内置的AI处理器(APU)工作频率可达500MHz,支持深度学习、神经网络加速和计算机视觉应用。配合高达2500万像素的摄像头,可以为AI相机应用提供清晰、精确的图像,如人脸识…...
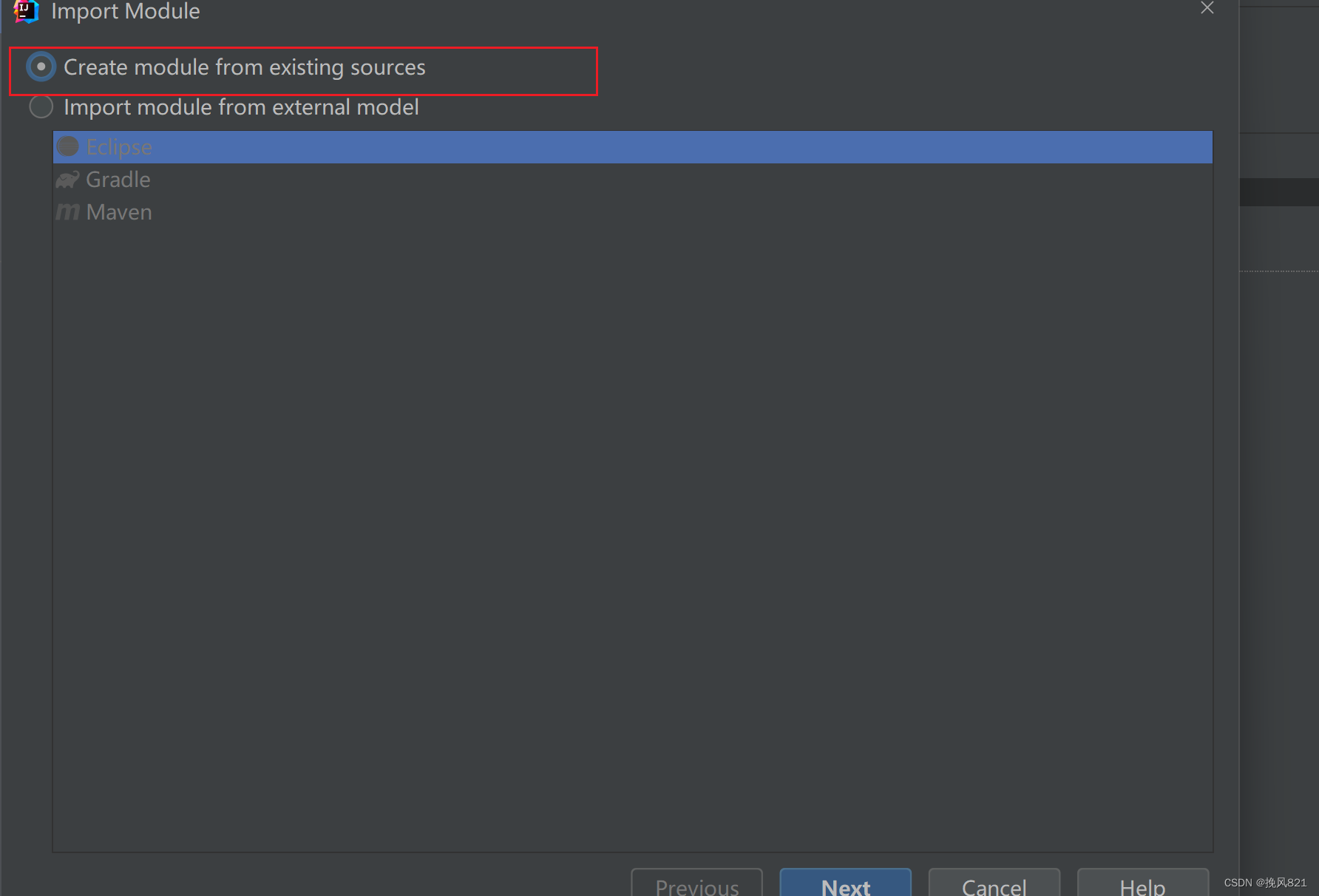
idea导入javaweb变成灰色
解决办法: 如果这时候src是蓝色,其余都是灰色文件夹,这时候要先把src文件夹变成灰色,否则之后会报错 src文件变成灰色方法,右键src,选择make direcory as 选择unmark 如果src不是蓝色,就是灰色࿰…...

SpringBoot集成Memcached
SpringBoot集成Memcached 1、Memcached 介绍 Memcached 是一个高性能的分布式内存对象缓存系统,用于动态Web应用以减轻数据库负载。它通过在内存中 缓存数据和对象来减少读取数据库的次数,从而提高动态、数据库驱动网站的速度。Memcached基于一个存储…...
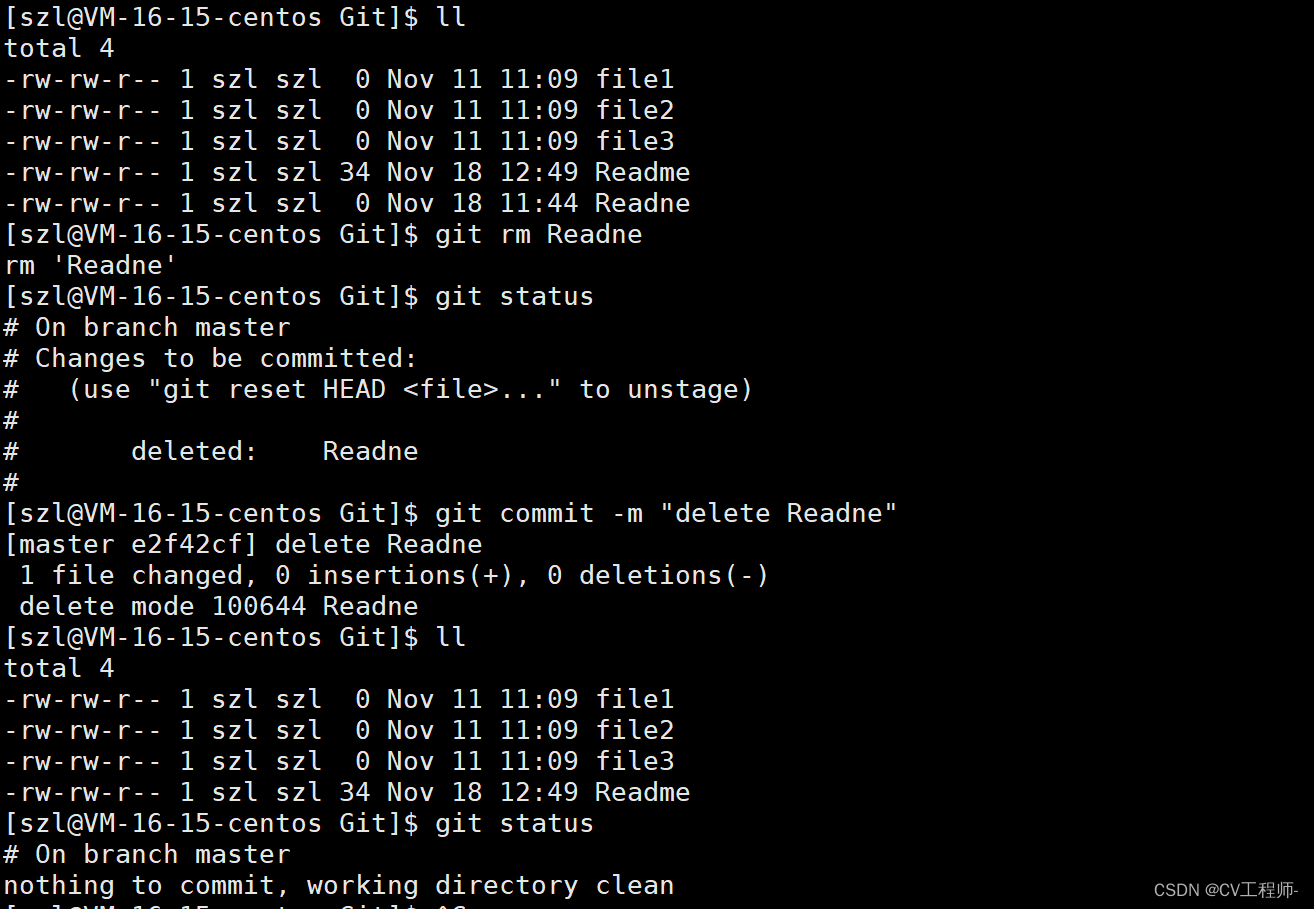
git基本操作(配图超详细讲解)
个人主页:Lei宝啊 愿所有美好如期而遇 目录 创建git本地仓库 配置仓库 认识工作区,暂存区,版本库 修改文件 版本回退 撤销修改 删除文件 创建git本地仓库 要提前说的是,仓库是进⾏版本控制的⼀个⽂件⽬录。我们要想对⽂…...

【网络通信】浅析UDP与TCP协议的奥秘
在现代互联网中,UDP(用户数据报协议)和TCP(传输控制协议)是两种最常用的传输协议,它们被广泛应用于网络数据传输。尽管这两种协议都可以用来在网络上传输数据,但它们在设计目标、特点和适用场景…...
C#核心笔记——(二)C#语言基础
一、C#程序 1.1 基础程序 using System; //引入命名空间namespace CsharpTest //将以下类定义在CsharpTest命名空间中 {internal class TestProgram //定义TestProgram类{public void Test() { }//定义Test方法} }方法是C#中的诸多种类的函数之一。另一种函数*,还…...

C++ 删除无头链上所有指定值为x的节点。
C 删除无头链上所有指定值为x的节点。 #include<stdio.h> #include<ctype.h> #include<stdlib.h> typedef struct app {int data;struct app* next; }APP; int main() {int n;int node;int x;while (scanf("%d", &n) ! EOF){APP* head NULL, …...
linux基本指令以及热键
基本指令 ♥clear ♥whoami ♥who ♥pwd ♥ls指令(重点) ls -a: ls -l ♥mkdir ♥cd指令 ♥touch指令 ♥stat指令 ♥rmdir指令 && rm 指令 ♥man指令 ♥nano指令 ♥cp指令 ♥mv指令 ♥cat指令 🗡输出/输出重定向 …...

Rocketmq消费消息时不丢失不重复
消息消费不丢失 手动ACK 在消费者端,需要确保在消息拉取并消费成功之后再给Broker返回ACK,就可以保证消息不丢失了,如果这个过程中Broker一直没收到ACK,那么就可以重试。所以,在消费者的代码中,一定要在业…...

RedisInsight——redis的桌面UI工具使用实践
下载 官网下载安装。下载地址在这里 填个邮箱地址就可以下载了。 安装使用。 安装成功后开始使用。 1. 你可以add一个地址。或者登录redis cloud 去auto-discover 2 . 新增你的redis库地址。注意index的取值 3。现在可以登录到redis了。看看结果 这是现在 在服务器上执行…...
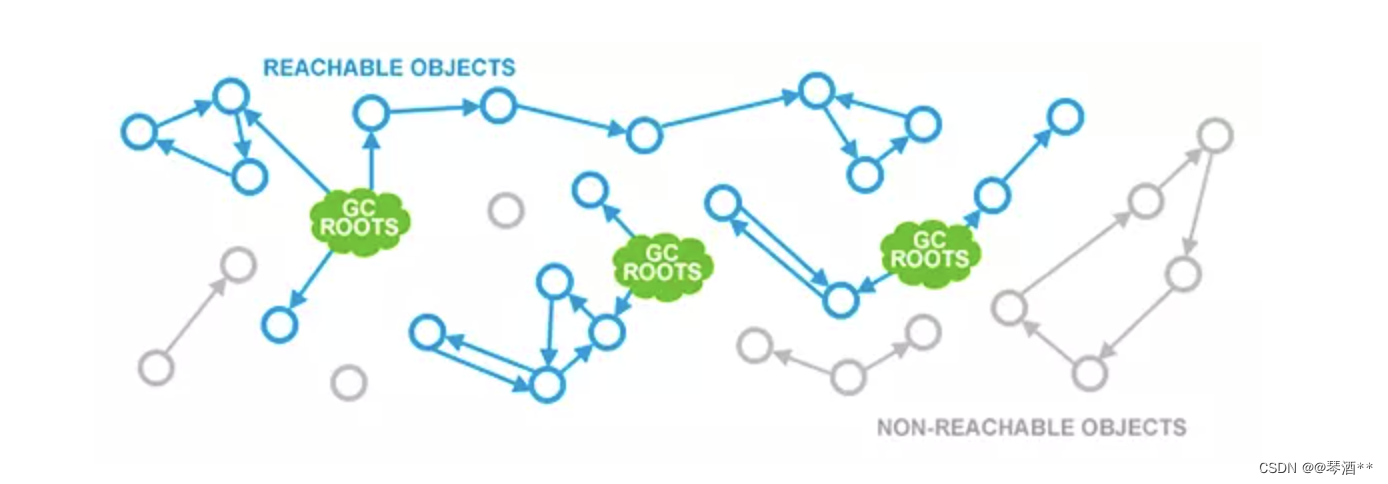
JVM对象创建与内存分配
对象的创建 对象创建的主要流程: 类加载推荐博客:JVM类加载机制详解 类加载检查 虚拟机遇到一条new指令时,首先将去检查这个指令的参数是否能在常量池中定位到一个类的符号引用,并且检查这个符号引用代表的类是否已被加载、解析…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
