002 OpenCV dft 傅里叶变换
目录
一、傅里叶变换
1.1 傅里叶变换概念
1.2 opencv中傅里叶变换
二、实验代码
一、环境
本文使用环境为:
- Windows10
- Python 3.9.17
- opencv-python 4.8.0.74
二、傅里叶变换
2.1 傅里叶变换概念
傅里叶变换(Fourier Transform)是一种在数学、物理和工程领域广泛应用的算法,用于分析信号或数据的频率成分。它是由法国数学家约瑟夫·傅里叶(Joseph Fourier)于19世纪初提出的,因此得名。傅里叶变换的基本思想是将一个时域信号转换为频域信号,或者将一个频域信号转换回时域信号。这种转换可以帮助我们更好地理解和分析信号的特性,例如幅度、频率和相位等。
傅里叶变换可以分为连续傅里叶变换(Continuous Fourier Transform,CFT)和离散傅里叶变换(Discrete Fourier Transform,DFT)。连续傅里叶变换用于处理连续时间信号,而离散傅里叶变换用于处理离散时间信号。在实际应用中,由于计算机处理的是离散数据,因此离散傅里叶变换更为常用。
离散傅里叶变换(DFT)的基本步骤如下:
-
对输入信号进行采样,得到离散时间信号。采样频率通常为原始信号频率的整数倍,以满足奈奎斯特采样定理。
-
对离散时间信号进行窗函数处理。窗函数的作用是减小信号截断引起的频谱泄漏,同时减小频谱旁瓣的影响。常用的窗函数有矩形窗、汉宁窗和海宁窗等。
-
计算离散时间信号的离散傅里叶变换。这可以通过快速傅里叶变换(Fast Fourier Transform,FFT)算法来实现,以提高计算效率。快速傅里叶变换是一种基于蝶形运算的高效算法,其计算复杂度为O(nlogn),其中n为信号长度。
-
对离散傅里叶变换的结果进行分析。通过观察频谱图,可以了解信号的频率分布、幅值和相位等信息。此外,还可以利用傅里叶变换的性质进行信号处理,例如滤波、降噪和压缩等。
傅里叶变换具有以下重要性质:
-
线性性质:傅里叶变换满足线性叠加原理,即两个信号的傅里叶变换之和等于这两个信号分别进行傅里叶变换后再相加的结果。
-
共轭对称性:对于实数信号,其傅里叶变换的共轭复数表示了信号的频谱。这意味着实数信号的频谱是以原点为中心的对称分布。
-
时移性质:对于任意实数τ,信号x(t)与其自身延时τ的信号x(t-τ)的傅里叶变换之比等于e^(j2πτ),其中j为虚数单位。这表明时移操作可以通过乘以复指数因子来实现。
-
频移性质:对于任意实数ω,信号x(t)与其频率为ω的信号cos(2πωt)的乘积的傅里叶变换等于X(f)与δ(f-ω)的卷积,其中δ(f)表示狄拉克δ函数。这表明频率调制可以通过乘以复指数因子和滤波操作来实现。
-
能量守恒:离散傅里叶变换的能量守恒性质表明,信号的总能量在时域和频域之间是平衡的。这意味着在频域中去除某些频率分量后,信号的总能量会相应地转移到其他频率分量上。
总之,傅里叶变换是一种强大的数学工具,广泛应用于通信、图像处理、音频处理、生物信息学等领域。通过傅里叶变换,我们可以更好地理解和分析信号的特性,从而实现信号的滤波、降噪、压缩等功能。
2.2 opencv中傅里叶变换
在数字图像处理中,空间域滤波和频域滤波都是常见的方法,但它们之间存在一些关键的区别。
-
空间域滤波:这种方法直接对图像进行操作,通常使用各种模板与图像进行卷积运算来实现图像的处理。由于其直接在图像空间上操作,这种方法的实现相对简单和直观。
-
频域滤波:频域滤波首先将图像从空间域转换到频域,然后对频率域中的图像数据进行处理,最后再将其转换回空间域。这种处理方法的优点在于,某些图像处理任务在频域中比在空间域中更为简单。例如,根据卷积定理,可以通过傅立叶变换将空域卷积滤波变换为频域滤波。此外,频域滤波允许设计者使用复杂的滤波器设计,这可能在空间域中难以实现。然而,需要注意的是,如果选用的频域滤波器具有陡峭的变化,可能会导致输出图像产生“振铃”现象,这是由于灰度剧烈变化处产生的。
在OpenCV库中,傅里叶变换和逆傅里叶变换的实现主要依赖于**cv2.dft()和cv2.idft()**两个函数。在进行傅里叶变换时,你需要将原始图像转换为np.float32格式。
具体来说,cv2.dft()函数的定义是:cv2.dft(原始图像,转换标识)。其中,原始图像必须是np.float32格式,转换标识用于说明是傅里叶变换还是傅里叶逆变换。此函数返回与前一个相同的结果,但是有两个通道。第一个通道是结果的实部,第二个通道是结果的虚部。
另一方面,cv2.idft()函数被用来执行逆傅里叶变换。例如,如果你有一个通过傅里叶变换得到的复数矩阵,你可以使用这个函数来恢复原始图像。
需要注意的是,OpenCV提供的这两个函数的效率较高(比OpenCV自带的函数快3倍)。这是因为它们实现了一种称为快速傅立叶变换(FFT)的快速算法。
三、实验代码
from __future__ import print_function
import sysimport cv2 as cv
import numpy as npdef print_help():print('''代码演示离散傅里叶变换,同时也显示幅度谱''')def main(argv):print_help()I = cv.imread("d:/Data/1.jpg", cv.IMREAD_GRAYSCALE)if I is None:print('Error opening image')return -1## [expand]rows, cols = I.shapem = cv.getOptimalDFTSize( rows )n = cv.getOptimalDFTSize( cols )# 把图像边界拓展下padded = cv.copyMakeBorder(I, 0, m - rows, 0, n - cols, cv.BORDER_CONSTANT, value=[0, 0, 0])## [complex_and_real]planes = [np.float32(padded), np.zeros(padded.shape, np.float32)]complexI = cv.merge(planes) # Add to the expanded another plane with zeros## [complex_and_real]## [dft]cv.dft(complexI, complexI) # this way the result may fit in the source matrix## [dft]# compute the magnitude and switch to logarithmic scale# = > log(1 + sqrt(Re(DFT(I)) ^ 2 + Im(DFT(I)) ^ 2))## [magnitude]cv.split(complexI, planes) # planes[0] = Re(DFT(I), planes[1] = Im(DFT(I))cv.magnitude(planes[0], planes[1], planes[0])# planes[0] = magnitudemagI = planes[0]## [magnitude]## [log]matOfOnes = np.ones(magI.shape, dtype=magI.dtype)cv.add(matOfOnes, magI, magI) # switch to logarithmic scale# 取log是为了拉伸值cv.log(magI, magI)## [log]## [crop_rearrange]magI_rows, magI_cols = magI.shape# crop the spectrum, if it has an odd number of rows or columnsmagI = magI[0:(magI_rows & -2), 0:(magI_cols & -2)]cx = int(magI_rows/2)cy = int(magI_cols/2)q0 = magI[0:cx, 0:cy] # Top-Left - Create a ROI per quadrantq1 = magI[cx:cx+cx, 0:cy] # Top-Rightq2 = magI[0:cx, cy:cy+cy] # Bottom-Leftq3 = magI[cx:cx+cx, cy:cy+cy] # Bottom-Righttmp = np.copy(q0) # 交换象限(左上和右下交换)magI[0:cx, 0:cy] = q3magI[cx:cx + cx, cy:cy + cy] = tmptmp = np.copy(q1) # 交换象限(右上和左下交换)magI[cx:cx + cx, 0:cy] = q2magI[0:cx, cy:cy + cy] = tmp# 归一化到 [0, 1]范围内cv.normalize(magI, magI, 0, 1, cv.NORM_MINMAX)# 原图得灰度图cv.imshow("Input Image" , I )# 幅度谱,也叫频谱cv.imshow("spectrum magnitude", magI)cv.waitKey()if __name__ == "__main__":main(sys.argv[1:])
原图:

灰度图:

幅度谱如下:中间是高频区域、边界是低频区域、幅度谱是关于图像中心对称的。

相关文章:

002 OpenCV dft 傅里叶变换
目录 一、傅里叶变换 1.1 傅里叶变换概念 1.2 opencv中傅里叶变换 二、实验代码 一、环境 本文使用环境为: Windows10Python 3.9.17opencv-python 4.8.0.74 二、傅里叶变换 2.1 傅里叶变换概念 傅里叶变换(Fourier Transform)是一种…...
)
力扣:171. Excel 表列序号(Python3)
题目: 给你一个字符串 columnTitle ,表示 Excel 表格中的列名称。返回 该列名称对应的列序号 。 例如: A -> 1 B -> 2 C -> 3 ... Z -> 26 AA -> 27 AB -> 28 ... 来源:力扣(LeetCode) …...

C++中结构体的初始化
C中结构体的初始化 结构体是一个由程序员定义的数据类型,可以容纳许多不同的数据值。在过去,面向对象编程的应用尚未普及之前,程序员通常使用这些从逻辑上连接在一起的数据组合到一个单元中。一旦结构体类型被声明并且其数据成员被标识&…...

vue3+vite+ts 发布自定义组件到npm
vue3vite 发布自定义组件到npm 初始化项目编写组件配置打包组件上传到npm测试组件库 初始化项目 // 创建项目 pnpm create vite vue-test-app --template vue-ts// 运行项目 cd vite vue-test-app pnpm install pnpm run dev编写组件 1、根目录下创建packages目录作为组件的开…...

mybatis使用xml形式配置
以这个注解形式的查询代码为例 Select("select * from emp where name like concat(%,#{name},%) and gender #{gender} and entrydate between #{begin} and #{end} order by update_time desc ")public List<Emp> list(String name, Short gender, LocalDat…...
开源简历生成器OpenResume
什么是 OpenResume ? OpenResume 是一个功能强大的开源简历生成器和简历解析器。OpenResume 的目标是为每个人提供免费的现代专业简历设计,让任何人都能充满信心地申请工作。 OpenResume 有 5 个核心特点: 特征描述1. 实时UI更新当您输入简历…...

AI变现之Gpts搞流量+赚钱
文章目录 Gpts | 搞流量 + 赚钱1.项目介绍2.项目分析3.项目实操4.变现路径Gpts | 搞流量 + 赚钱 1.项目介绍 这两天 AI 圈最火的莫过于 OpenAI 开发者大会公布的一个爆炸产品 Gpts 了,大家都知道这个肯定是一个划时代的产品,也绝对是一个风口,虽然官方还没有公布到底怎么通…...
)
音视频项目—基于FFmpeg和SDL的音视频播放器解析(十六)
介绍 在本系列,我打算花大篇幅讲解我的 gitee 项目音视频播放器,在这个项目,您可以学到音视频解封装,解码,SDL渲染相关的知识。您对源代码感兴趣的话,请查看基于FFmpeg和SDL的音视频播放器 如果您不理解本…...

Elasticsearch文档操作
一、Elasticsearch的CURD 1、CURD之Create PUT lqz/doc/1 {"name":"顾老二","age":30,"from": "gu","desc": "皮肤黑、武器长、性格直","tags": ["黑", "长", "直…...
聊一聊go的单元测试(goconvey、gomonkey、gomock)
文章目录 概要一、测试框架1.1、testing1.2、stretchr/testify1.3、smartystreets/goconvey1.4、cweill/gotests 二、打桩和mock2.1、打桩2.2、mock2.2.1、mockgen2.2.1、示例 三、基准测试和模糊测试3.1、基准测试3.2、模糊测试 四、总结4.1、小结4.2、其他4.3、参考资料 概要…...

Positive Technologies 利用 PT Cloud Application Firewall 保护中小型企业的网络资源
云产品按月订购,无需购买硬件资源 PT Cloud Application Firewall 是 Positive Technologies 推出的首个用于保护网络应用程序的商用云产品。Web 应用层防火墙 (web application firewall, WAF) 现在可以通过 技术合作伙伴——授权服务商和云提供商以订购方式提供1…...
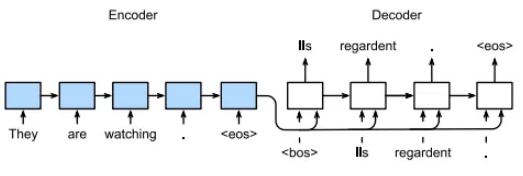
深入解析序列模型:全面阐释 RNN、LSTM 与 Seq2Seq 的秘密
探索序列建模的基础知识和应用。 简介 序列建模是许多领域的一个重要问题,包括自然语言处理 (NLP)、语音识别和语音合成、时间序列预测、音乐生成和「生物信息学」。所有这些任务的共同点是它们需要坚持。接下来的事情的预测是基于历史的。例如,在“哈桑…...

vue项目本地开发构建速度优化 hard-source-webpack-plugin
1、为啥要优化本地构建速度 有些项目因为项目需求点多、功能复杂、管理混乱、引入第三方插件/样式库过多、本身项目页面较多、文件较多等等原因,会导致项目体积变大、本地构建速度明显变慢,这时就需要对项目webpack进行一些设置来提高打包效率、加快打包…...

燕之屋通过港交所聆讯:苦战IPO十余年,黄健等人提前精准套现
撰稿|行星 来源|贝多财经 11月19日,厦门燕之屋生物工程股份有限公司(下称“燕之屋”)通过港交所聆讯,并披露了聆讯后资料集(即招股书),中金公司和广发证券为其联席保荐人。 据贝多财经了解&a…...

【51单片机系列】C51基础
本文内容是关于C51语言的基础内容的,包括C51的数据类型、变量、运算符、函数以及reg52.h文件中的内容,有些与C中相同的内容没有记录在此,比如常量、某些变量、表达式、程序结构、数组等没有涉及。 文章目录 C51的数据类型1. C51中的基本数据类…...
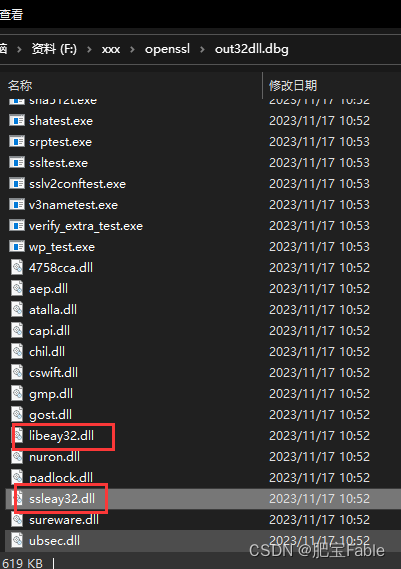
openssl1.0.2版本Windows安装问题
之前安装过1.1版本,Windows环境下C 安装OpenSSL库 源码编译及使用(VS2019)_vs2019安装openssl_肥宝Fable的博客-CSDN博客 后来发现linux编译不过,以为是版本问题,相差太大,所以降一下版本,以免…...

【Java 进阶篇】Ajax 实现——原生JS方式
大家好,欢迎来到这篇关于原生 JavaScript 中使用 Ajax 实现的博客!在前端开发中,我们经常需要与服务器进行数据交互,而 Ajax(Asynchronous JavaScript and XML)是一种用于创建异步请求的技术,它…...
Spring Cloud Stream实践
概述 不同中间件,有各自的使用方法,代码也不一样。 可以使用Spring Cloud Stream解耦,切换中间件时,不需要修改代码。实现方式为使用绑定层,绑定层对生产者和消费者提供统一的编码方式,需要连接不同的中间…...

高精度算法【Java】(待更新中~)
高进度加法 在Java中可以使用BigInteger进行高精度计算,除此也可以仿照竖式相加的计算原理进行计算。 BigInteger 提供所有 Java 的基本整数操作符的对应物,并提供 java.lang.Math 的所有相关方法。另外,BigInteger 还提供以下运算࿱…...

说一说HTTP1.0、1.1、2.0版本区别和优化
说一说HTTP1.0、1.1、2.0版本区别和优化 HTTP(Hypertext Transfer Protocol)是一种用于传输超文本的应用层协议。 在不同的版本中,HTTP经历了一系列的演进和改进,主要包括HTTP 1.0、HTTP 1.1和HTTP 2.0。 下面详细解释它们之间…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
