力扣刷题-二叉树-二叉树最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。(注意题意)
示例 1:
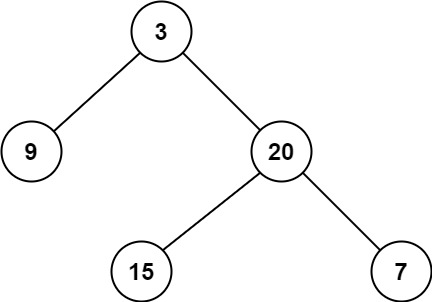
输入:root = [3,9,20,null,null,15,7]
输出:2
层序遍历法
# 层序遍历法
class Solution(object):def minDepth(self, root):""":type root: TreeNode:rtype: int"""if not root:return 0queue = deque([(root, 1)]) # 每个元素是元组 一个是树元素值 一个是最小深度 比较巧妙while queue:cur, min_depth = queue.popleft()if not cur.left and not cur.right:return min_depthif cur.left:queue.append((cur.left, min_depth+1))if cur.right:queue.append((cur.right, min_depth+1))return 0
时间复杂度:O(N) 因为每个结点会访问一次
空间复杂度:O(N)在层序遍历法中空间复杂度主要取决于队列的开销,队列中的元素个数不会超过树的节点数。
递归法
注意这块和最大深度不一样,如下是错误代码:说明:叶子节点是指没有子节点的节点。(注意题意)

这个代码就犯了此图中的误区:说明:叶子节点是指没有子节点的节点。(注意题意)
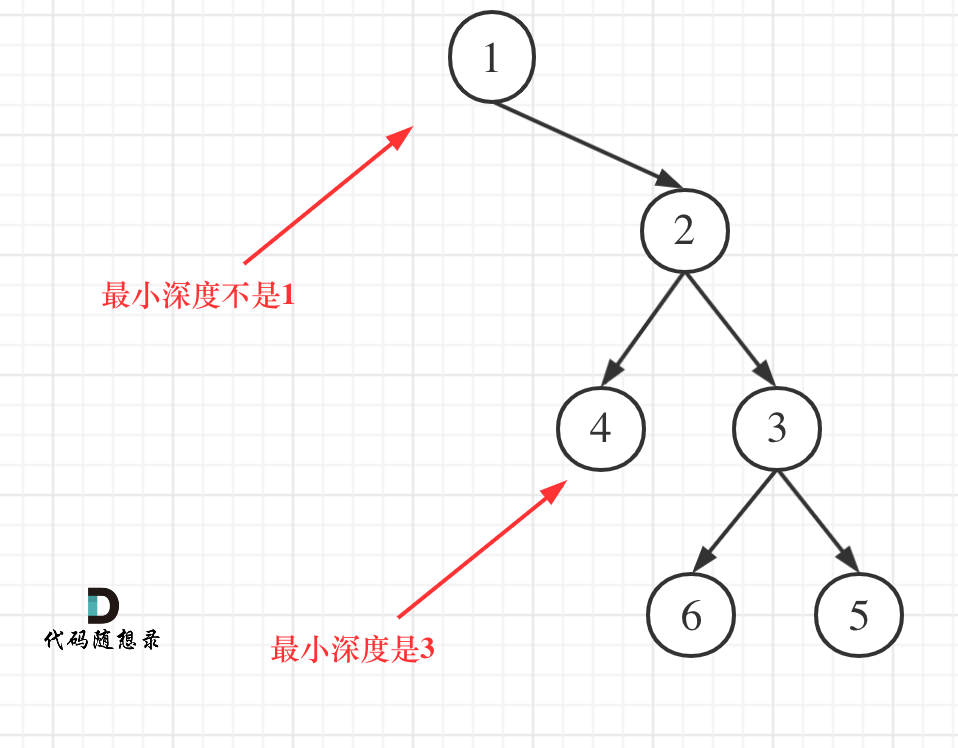
如果这么求的话,没有左孩子的分支会算为最短深度。
所以,如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空,返回左右子树深度最小值 + 1 。

# 递归法
class Solution(object):def minDepth(self, root):""":type root: TreeNode:rtype: int"""return self.getDepth(root)def getDepth(self, node):if node is None:return 0leftDepth = self.getDepth(node.left) # 左rightDepth = self.getDepth(node.right) # 右# 中# 当一个左子树为空,右不为空,这时并不是最低点if node.left is None and node.right is not None:return 1 + rightDepth# 当一个右子树为空,左不为空,这时并不是最低点if node.left is not None and node.right is None:return 1 + leftDepthresult = 1 + min(leftDepth, rightDepth)return result
时间复杂度:O(N),其中 N 是树的节点数。对每个节点访问一次。
空间复杂度:O(N)/O(H) 其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销,最坏情况下,树呈现链状,空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关,空间复杂度为 O(logN)
参考:
https://www.programmercarl.com/0111.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E6%9C%80%E5%B0%8F%E6%B7%B1%E5%BA%A6.html
相关文章:

力扣刷题-二叉树-二叉树最小深度
给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明:叶子节点是指没有子节点的节点。(注意题意) 示例 1: 输入:root [3,9,20,null,null,15,7] 输出&#x…...
注解方式优雅的实现 Redisson 分布式锁
1前言 日常开发中,难免遇到一些并发的场景,为了保证接口执行的一致性,通常采用加锁的方式,因为服务是分布式部署模式,本地锁Reentrantlock和Synchnorized这些就先放到一边了,Redis的setnx锁存在无法抱保证…...
PHP/Laravel通过经纬度计算距离获取附近商家
实际开发中,常常需要获取用户附近的商家,思路是 获取用户位置(经纬度信息)在数据库中查询在距离范围内的商家 注: 本文章内计算距离所使用地球半径统一为 6378.138 km public function mpa_list($latitude,$longitude,$distance){// $latitude 34.306465;// $longitude 10…...

grafana面板介绍
grafana 快速使用 背景 随着公司业务的不断发展,紧接来的是业务种类的增加、服务器数量的增长、网络环境的越发复杂以及发布更加频繁,从而不可避免地带来了线上事故的增多,因此需要对服务器到应用的全方位监控,提前预警…...
)
实验三 循环结构程序设计(Python)
第1关:打印图形 zm=input("") #代码开始#代码结束def print_pattern(letter):if not letter.isalpha() or not letter.isupper():print("请输入大写字母")returnstart_char = Aend_char = letterfor i in range(ord(start_char), ord(end_char) + 1):spa…...
)
Flutter笔记:目录与文件存储以及在Flutter中的使用(上)
Flutter笔记 目录与文件存储以及在Flutter中的使用(上) 文件系统基础知识与路径操作 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:h…...

注意了!申请流量卡时地址一定不要填写学校,不好下卡哦!
当我们在网上购买流量卡时,都会要求让填写准确的收货地址,但是对于收货地址你填对了吗? 很多朋友在提交流量卡申请之后,往往会被运营商拒审,对于拒审的原因除了比较常见的信息填写有有误、涉及禁发地区、重复申…...

minio使用shell上传文件
minio使用shell上传文件 前言1. 编写调用脚本2.测试脚本上传3.候选脚本 前言 业务场景需要实现,服务器文件上传至存储服务。一种方式是安装minio的linux客户端,另一种方式是通过调用minio的api接口实现文件上传。后一种方式不需要依赖minio的客户端使用…...

LeetCode538. Convert BST to Greater Tree
文章目录 一、题目二、题解 一、题目 Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST. As a remin…...

iPaaS和RPA,企业自动化应该如何选择?
全球著名的咨询调查机构Gartner在2022年初再次发布了《2022年12大技术趋势》报告。 Gartner是全球最具权威的IT研究与顾问咨询公司,成立于1979年,在界定及分析那些决定了商业进程的发展趋势与技术方面,它拥有二十年以上的丰富经验,…...
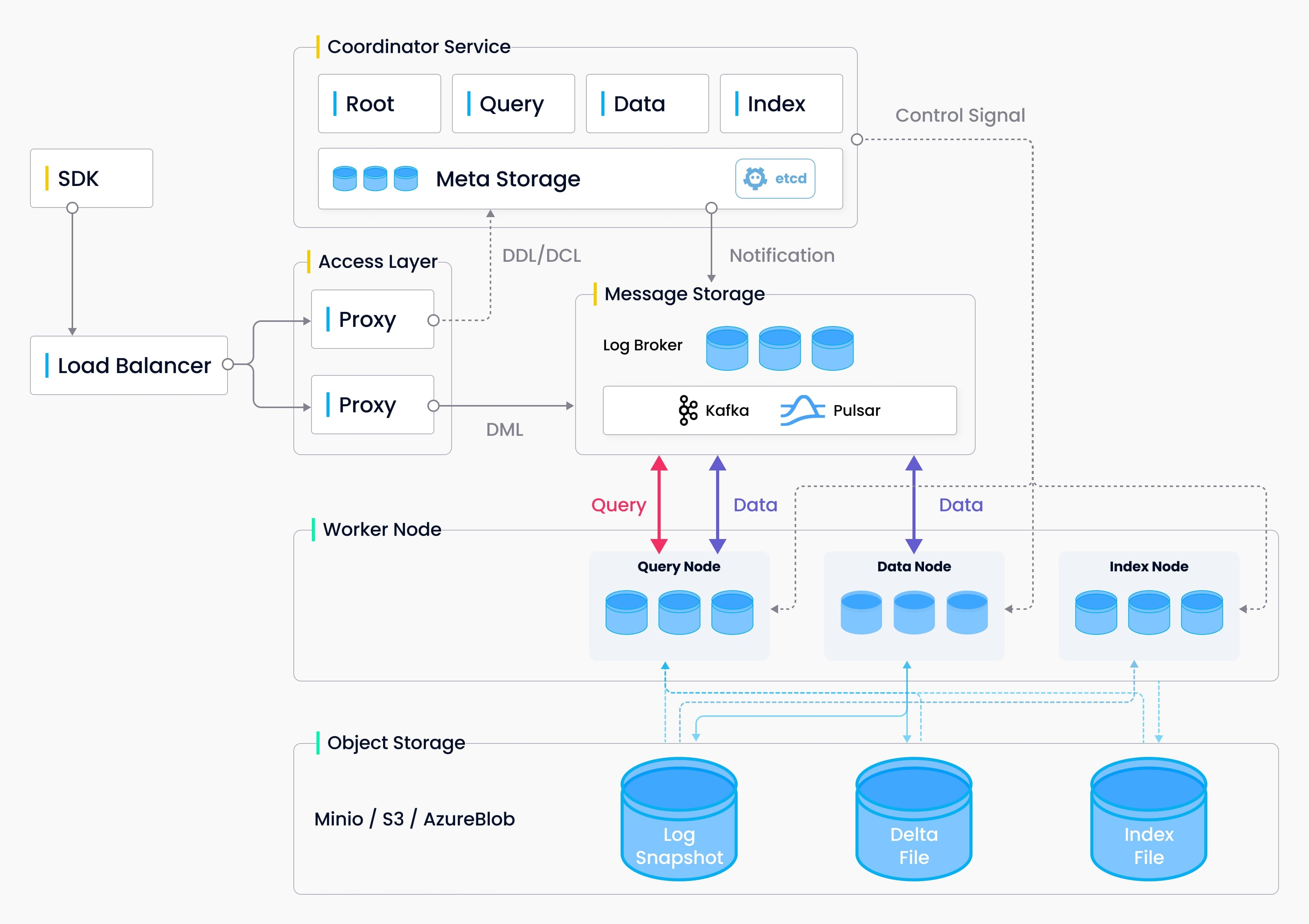
AI实践与学习1_Milvus向量数据库实践与原理分析
前言 随着NLP预训练模型(大模型)以及多模态研究领域的发展,向量数据库被使用的越来越多。 在XOP亿级题库业务背景下,对于试题召回搜索单单靠着ES集群已经出现性能瓶颈,因此需要预研其他技术方案提高试题搜索召回率。…...

3Dexcite deltgen 2022x 新功能
3DEXCITE DELTAGEN 2022x 现已发布,此次新版发布包含 DELTAGEN 2022x,DELTAGEN MARKETING SUITE 2022x,DELTAGEN XPLORE 2022x,以及软件开发工具包 SDK FOR DELTAGEN 2022x 版本。赶快来获取最新 DG 版本,了解新增内容…...

代码随想录算法训练营第六十天 | LeetCode 84. 柱状图中最大的矩形
代码随想录算法训练营第六十天 | LeetCode 84. 柱状图中最大的矩形 文章链接:柱状图中最大的矩形 视频链接:柱状图中最大的矩形 1. LeetCode 84. 柱状图中最大的矩形 1.1 思路 本题是给一个数组形象得画出图后求矩形的最大面积是多少。本题和42. 接雨水…...

【2023云栖】陈守元:阿里云开源大数据产品年度发布
本文根据 2023 云栖大会演讲实录整理而成,演讲信息如下: 演讲人:陈守元 | 阿里云计算平台事业部开源大数据产品总监 演讲主题:阿里云开源大数据产品年度发布 随着云计算的不断发展,未来数据处理和应用的趋势将围绕C…...

Element UI 禁用数字输入框组件添加鼠标滚动事件
Element UI 禁用数字输入框组件添加鼠标滚动事件 <el-input type"number" mousewheel.native.prevent DOMMouseScroll.native.prevent :min"0" onkeyup"this.valuethis.value.match(/\d\.?\d{0,2}/);"v-model"form.threeYearDevelop…...
担忧CentOS停服?KeyarchOS系统来支撑
担忧CentOS停服?KeyarchOS系统来支撑 近年发生的“微软黑屏门”、“微软操作系统停更”等安全事件,敲响了我国 IT 产业的警钟,建立由我国主导的 IT 产业生态尤为迫切。对此,我国信息技术应用创新行业乘势而起,旨在通过…...

聚观早报 |联想集团Q2财季业绩;小鹏汽车Q3营收
【聚观365】11月17日消息 联想集团Q2财季业绩 小鹏汽车Q3营收 微软发布两款自研AI芯片 FAA批准SpaceX再次发射星际飞船 2023 OPPO开发者大会 联想集团Q2财季业绩 全球数字经济领导企业联想集团公布截至2023年9月30日的2023/24财年第二财季业绩:整体营收达到10…...

SAP ABAP权限控制中常用TCODE
权限控制中的几个TCODE 1.创建新的权限对象并在程序中使用 利用SU21创建权限对象Z_TEST,在程序中检查授权。 检查的代码如下: AUTHORITY-CHECK OBJECT ‘Z_TEST’ID ‘ACTION’ FIELD ‘44′ID ‘BUKRS’ FIELD DUMMY .IF sy-subrc NE 0.MESSAGE e00…...
云计算赛项容器云2023搭建
部署容器云平台[5 分] 使 用 OpenStack 私 有 云 平 台 创 建 两 台 云 主 机 , 云 主 机 类 型 使 用 4vCPU/12G/100G 类型,分别作为 Kubernetes 集群的 Master 节点和 node 节点, 然后完成 Kubernetes 集群的部署,并完成 Istio …...

11.1 文件拷贝移动与删除
在编程中,针对磁盘与目录的操作也是非常重要的,本章将重点介绍如何实现针对文件目录与磁盘的操作方法,其中包括了删除文件,文件拷贝,文件读写,目录遍历输出,遍历磁盘容量信息,磁盘格…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
