周赛372(正难则反、枚举+贪心、异或位运算、离线+单调栈)
文章目录
- 周赛372
- [2937. 使三个字符串相等](https://leetcode.cn/problems/make-three-strings-equal/)
- 模拟(正难则反)
- [2938. 区分黑球与白球](https://leetcode.cn/problems/separate-black-and-white-balls/)
- 枚举 + 贪心
- [2939. 最大异或乘积](https://leetcode.cn/problems/maximum-xor-product/)
- 位运算 - 异或性质
- [2940. 找到 Alice 和 Bob 可以相遇的建筑](https://leetcode.cn/problems/find-building-where-alice-and-bob-can-meet/)
- 离线 + 单调栈
周赛372
2937. 使三个字符串相等
简单
给你三个字符串 s1、s2 和 s3。 你可以根据需要对这三个字符串执行以下操作 任意次数 。
在每次操作中,你可以选择其中一个长度至少为 2 的字符串 并删除其 最右位置上 的字符。
如果存在某种方法能够使这三个字符串相等,请返回使它们相等所需的 最小 操作次数;否则,返回 -1。
示例 1:
输入:s1 = "abc",s2 = "abb",s3 = "ab"
输出:2
解释:对 s1 和 s2 进行一次操作后,可以得到三个相等的字符串。
可以证明,不可能用少于两次操作使它们相等。
示例 2:
输入:s1 = "dac",s2 = "bac",s3 = "cac"
输出:-1
解释:因为 s1 和 s2 的最左位置上的字母不相等,所以无论进行多少次操作,它们都不可能相等。因此答案是 -1 。
提示:
1 <= s1.length, s2.length, s3.length <= 100s1、s2和s3仅由小写英文字母组成。
模拟(正难则反)
class Solution {/**要求三个字符串相等,删除比较困难则直接从i=0开始比较字符是否相等*/public int findMinimumOperations(String s1, String s2, String s3) {int minlen = Math.min(s1.length(), Math.min(s2.length(), s3.length()));int res = 0;int samepos = 0;for(; samepos < minlen; samepos++){if(s1.charAt(samepos) != s2.charAt(samepos) ||s1.charAt(samepos) != s3.charAt(samepos)){break;}}if(samepos == 0) return -1;return s1.length() - samepos + s2.length() - samepos + s3.length() - samepos;}
}
比赛写的正的丑陋代码
class Solution {public int findMinimumOperations(String s1, String s2, String s3) {String[] strs = new String[3];strs[0] = s1;strs[1] = s2;strs[2] = s3;Arrays.sort(strs, (a, b) -> a.length() - b.length());int cnt = 0, len = strs[0].length();if(strs[0].length() != strs[2].length()){int tmp = strs[2].length();cnt += tmp - len;strs[2] = strs[2].substring(0, len);}if(strs[0].length() != strs[1].length()){int tmp = strs[1].length();cnt += tmp - len;strs[1] = strs[1].substring(0, len);}while(len > 0 && (!strs[0].equals(strs[1]) || !strs[0].equals(strs[2]))){len -= 1;strs[0] = strs[0].substring(0, len);strs[1] = strs[1].substring(0, len);strs[2] = strs[2].substring(0, len);cnt += 3;}if(len == 0) return -1;return cnt;}
}
2938. 区分黑球与白球
中等
桌子上有 n 个球,每个球的颜色不是黑色,就是白色。
给你一个长度为 n 、下标从 0 开始的二进制字符串 s,其中 1 和 0 分别代表黑色和白色的球。
在每一步中,你可以选择两个相邻的球并交换它们。
返回「将所有黑色球都移到右侧,所有白色球都移到左侧所需的 最小步数」。
示例 1:
输入:s = "101"
输出:1
解释:我们可以按以下方式将所有黑色球移到右侧:
- 交换 s[0] 和 s[1],s = "011"。
最开始,1 没有都在右侧,需要至少 1 步将其移到右侧。
示例 2:
输入:s = "100"
输出:2
解释:我们可以按以下方式将所有黑色球移到右侧:
- 交换 s[0] 和 s[1],s = "010"。
- 交换 s[1] 和 s[2],s = "001"。
可以证明所需的最小步数为 2 。
示例 3:
输入:s = "0111"
输出:0
解释:所有黑色球都已经在右侧。
提示:
1 <= n == s.length <= 105s[i]不是'0',就是'1'。
枚举 + 贪心
class Solution {/**倒序枚举,什么时候会将黑色球进行移动?当枚举到i位时是黑球,就要移动到靠近黑球的位置移动几次? i右边白球出现的次数*/public long minimumSteps(String s) {long res = 0;int cntw = 0, n = s.length();for(int i = n-1; i >= 0; i--){if(s.charAt(i) == '0'){cntw += 1;continue;}res += cntw;}return res;}
}
2939. 最大异或乘积
中等
给你三个整数 a ,b 和 n ,请你返回 (a XOR x) * (b XOR x) 的 最大值 且 x 需要满足 0 <= x < 2n。
由于答案可能会很大,返回它对 109 + 7 取余 后的结果。
注意,XOR 是按位异或操作。
示例 1:
输入:a = 12, b = 5, n = 4
输出:98
解释:当 x = 2 时,(a XOR x) = 14 且 (b XOR x) = 7 。所以,(a XOR x) * (b XOR x) = 98 。
98 是所有满足 0 <= x < 2n 中 (a XOR x) * (b XOR x) 的最大值。
示例 2:
输入:a = 6, b = 7 , n = 5
输出:930
解释:当 x = 25 时,(a XOR x) = 31 且 (b XOR x) = 30 。所以,(a XOR x) * (b XOR x) = 930 。
930 是所有满足 0 <= x < 2n 中 (a XOR x) * (b XOR x) 的最大值。
示例 3:
输入:a = 1, b = 6, n = 3
输出:12
解释: 当 x = 5 时,(a XOR x) = 4 且 (b XOR x) = 3 。所以,(a XOR x) * (b XOR x) = 12 。
12 是所有满足 0 <= x < 2n 中 (a XOR x) * (b XOR x) 的最大值。
提示:
0 <= a, b < 2500 <= n <= 50
位运算 - 异或性质
https://leetcode.cn/problems/maximum-xor-product/solutions/2532915/o1-zuo-fa-wei-yun-suan-de-qiao-miao-yun-lvnvr/
class Solution {/**位运算 (a XOR x) * (b XOR x) 1. a和b 对于同一个比特位 如果一个是0 另一个是1,那么无论x填0还是1,这个比特位的结果总是0或者12. 推论1: 在把同为 0 的比特位 改成 1 后,1 的总数是不变的3. 推论2: ax = a^x ; bx = b^x ax + bx 是一个定值==> 问题转化为:在 ax + bx是一个定值的情况下,求 ax * bx 的最大值均值定理 基本不等式==> 让 ax 和 bx 尽量接近(差的绝对值尽量小)分配方案:如果大于等于n的比特位 a=b,那么把最高位的1给ax,其余的1给bx如果大于等于n的比特位 a>b,那么把低于n的1都给b*/public int maximumXorProduct(long a, long b, int n) {if (a < b) {// 保证 a >= blong temp = a;a = b;b = temp;}long mask = (1L << n) - 1;long ax = a & ~mask; // 第 n 位及其左边,无法被 x 影响,先算出来long bx = b & ~mask;a &= mask; // 低于第 n 位,能被 x 影响b &= mask;long left = a ^ b; // 可分配:a XOR x 和 b XOR x 一个是 1 另一个是 0long one = mask ^ left; // 无需分配:a XOR x 和 b XOR x 均为 1ax |= one; // 先加到异或结果中bx |= one;// 现在要把 left 分配到 ax 和 bx 中// 根据基本不等式(均值定理),分配后应当使 ax 和 bx 尽量接近,乘积才能尽量大if (left > 0 && ax == bx) {// 尽量均匀分配,例如把 1111 分成 1000 和 0111long highBit = 1L << (63 - Long.numberOfLeadingZeros(left));ax |= highBit;left ^= highBit;}// 如果 a & ~mask 更大,则应当全部分给 bx(注意最上面保证了 a>=b)bx |= left;final long MOD = 1_000_000_007;return (int) (ax % MOD * (bx % MOD) % MOD); // 注意不能直接 long * long,否则溢出}
}
2940. 找到 Alice 和 Bob 可以相遇的建筑
困难
给你一个下标从 0 开始的正整数数组 heights ,其中 heights[i] 表示第 i 栋建筑的高度。
如果一个人在建筑 i ,且存在 i < j 的建筑 j 满足 heights[i] < heights[j] ,那么这个人可以移动到建筑 j 。
给你另外一个数组 queries ,其中 queries[i] = [ai, bi] 。第 i 个查询中,Alice 在建筑 ai ,Bob 在建筑 bi 。
请你能返回一个数组 ans ,其中 ans[i] 是第 i 个查询中,Alice 和 Bob 可以相遇的 最左边的建筑 。如果对于查询 i ,Alice 和 Bob 不能相遇,令 ans[i] 为 -1 。
示例 1:
输入:heights = [6,4,8,5,2,7], queries = [[0,1],[0,3],[2,4],[3,4],[2,2]]
输出:[2,5,-1,5,2]
解释:第一个查询中,Alice 和 Bob 可以移动到建筑 2 ,因为 heights[0] < heights[2] 且 heights[1] < heights[2] 。
第二个查询中,Alice 和 Bob 可以移动到建筑 5 ,因为 heights[0] < heights[5] 且 heights[3] < heights[5] 。
第三个查询中,Alice 无法与 Bob 相遇,因为 Alice 不能移动到任何其他建筑。
第四个查询中,Alice 和 Bob 可以移动到建筑 5 ,因为 heights[3] < heights[5] 且 heights[4] < heights[5] 。
第五个查询中,Alice 和 Bob 已经在同一栋建筑中。
对于 ans[i] != -1 ,ans[i] 是 Alice 和 Bob 可以相遇的建筑中最左边建筑的下标。
对于 ans[i] == -1 ,不存在 Alice 和 Bob 可以相遇的建筑。
示例 2:
输入:heights = [5,3,8,2,6,1,4,6], queries = [[0,7],[3,5],[5,2],[3,0],[1,6]]
输出:[7,6,-1,4,6]
解释:第一个查询中,Alice 可以直接移动到 Bob 的建筑,因为 heights[0] < heights[7] 。
第二个查询中,Alice 和 Bob 可以移动到建筑 6 ,因为 heights[3] < heights[6] 且 heights[5] < heights[6] 。
第三个查询中,Alice 无法与 Bob 相遇,因为 Bob 不能移动到任何其他建筑。
第四个查询中,Alice 和 Bob 可以移动到建筑 4 ,因为 heights[3] < heights[4] 且 heights[0] < heights[4] 。
第五个查询中,Alice 可以直接移动到 Bob 的建筑,因为 heights[1] < heights[6] 。
对于 ans[i] != -1 ,ans[i] 是 Alice 和 Bob 可以相遇的建筑中最左边建筑的下标。
对于 ans[i] == -1 ,不存在 Alice 和 Bob 可以相遇的建筑。
提示:
1 <= heights.length <= 5 * 1041 <= heights[i] <= 1091 <= queries.length <= 5 * 104queries[i] = [ai, bi]0 <= ai, bi <= heights.length - 1
离线 + 单调栈
https://leetcode.cn/problems/find-building-where-alice-and-bob-can-meet/solutions/2533058/chi-xian-zui-xiao-dui-pythonjavacgo-by-e-9ewj/
class Solution {/**给定一组询问,通常可思考离线做法,将询问分组,按某一种顺序进行回答题意:左边矮跳到右边高分类讨论 对于每个询问 i 和 j,假设 i <= j1. 如果 i == j,答案就是 j2. 如果 heights[i] < heights[j], i 可以直接跳到j,答案就是j3. 如果 heights[i] > heights[j],左边高右边矮,怎么跳?按照j分类 [0,1],[0,3],[2,4],[3,4],[2,2]j = 1 [0, 1]j = 2 无需回答,答案就是2j = 3 [0, 3]j = 4 [2, 4],[3, 4]整理好询问后,从左到右遍历建筑,如果发现当前 idx 建筑高度 > 之前需要回答的一个询问的建筑高度那么,这个询问的答案就是 idx需要一个最小堆去维护这些询问,每次取出最小的 heights[i],去和 heights[idx] 比较如果 heights[i] < heights[idx] 就立刻回答 (答案就是 idx)最后堆中剩下的询问 答案都是-1*/public int[] leftmostBuildingQueries(int[] heights, int[][] queries) {int[] ans = new int[queries.length];Arrays.fill(ans, -1);List<int[]>[] left = new ArrayList[heights.length];Arrays.setAll(left, e -> new ArrayList<>());for(int qi = 0; qi < queries.length; qi++){int i = queries[qi][0], j = queries[qi][1];if(i > j){ // 保证 i <= jint tmp = i; i = j; j = tmp;}if(i == j || heights[i] < heights[j]){ans[qi] = j; // i 直接跳到 j}else{left[j].add(new int[]{heights[i], qi});}}PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);for (int i = 0; i < heights.length; i++) { // 从小到大枚举下标 iwhile (!pq.isEmpty() && pq.peek()[0] < heights[i]) {ans[pq.poll()[1]] = i; // 可以跳到 i(此时 i 是最小的)}for (int[] p : left[i]) {pq.offer(p); // 后面再回答}}return ans;}
}
相关文章:
)
周赛372(正难则反、枚举+贪心、异或位运算、离线+单调栈)
文章目录 周赛372[2937. 使三个字符串相等](https://leetcode.cn/problems/make-three-strings-equal/)模拟(正难则反) [2938. 区分黑球与白球](https://leetcode.cn/problems/separate-black-and-white-balls/)枚举 贪心 [2939. 最大异或乘积](https:/…...
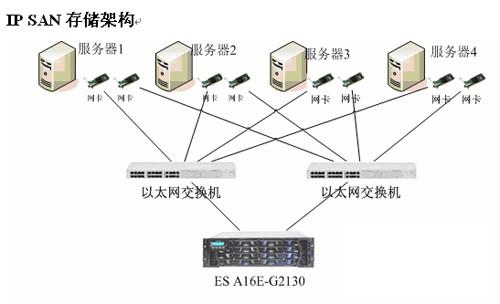
存储区域网络(SAN)之FC-SAN和IP-SAN的比较
存储区域网络(Storage Area Network,SAN)用于将多个系统连接到存储设备和子系统。 早期FC-SAN: 采用光纤通道(Fibre Channel,FC)技术,通过光纤通道交换机连接存储阵列和服务器主机,建立专用于数据存储的区域网络。 传…...

Leetcode_45:跳跃游戏 II
题目描述: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i] i j < n 返…...

给新手教师的成长建议
随着教育的不断发展和进步,越来越多的新人加入到教师这个行列中来。从学生到教师,这是一个华丽的转身,需要我们不断地学习和成长。作为一名新手老师,如何才能快速成长呢?以下是一名老师教师给的几点建议: 一…...

新手教师如何迅速成长
对于许多新手教师来说,迈出教学的第一步可能会感到非常困难。不过,通过一些关键的策略和技巧,还是可以快速提升教学能力的,我将为大家提供一些实用的建议,帮助各位在教育领域迅速成长。 深入了解学科知识 作为一名老师…...
竞赛选题 深度学习验证码识别 - 机器视觉 python opencv
文章目录 0 前言1 项目简介2 验证码识别步骤2.1 灰度处理&二值化2.2 去除边框2.3 图像降噪2.4 字符切割2.5 识别 3 基于tensorflow的验证码识别3.1 数据集3.2 基于tf的神经网络训练代码 4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 &#x…...
提升工作效率,使用AnyTXT Searcher实现远程办公速查公司电脑文件——“cpolar内网穿透”
文章目录 前言1. AnyTXT Searcher1.1 下载安装AnyTXT Searcher 2. 下载安装注册cpolar3. AnyTXT Searcher设置和操作3.1 AnyTXT结合cpolar—公网访问搜索神器3.2 公网访问测试 4. 固定连接公网地址 前言 你是否遇到过这种情况,异地办公或者不在公司,想找…...

mybatis使用foreach标签实现union集合操作
最近遇到一个场景就是Java开发中,需要循环多个表名,然后用同样的查询操作分别查表,最终得到N个表中查询的结果集合。在查询内容不一致时Java中跨表查询常用的是遍历表名集合循环查库,比较耗费资源,效率较低。在查询内容…...

请问DasViewer是否支持与业务系统集成,将业务的动态的数据实时的展示到三维模型上?
答:一般这种是以平台的方式来展示,云端地球实景三维建模云平台是专门做这一块的,可前往云端地球官网免费使用。 DasViewer是由大势智慧自主研发的免费的实景三维模型浏览器,采用多细节层次模型逐步自适应加载技术,让用户在极低的电脑配置下,…...

[ruby on rails]rack-cors, rack-attack
gem rack-attack gem rack-cors1. rack-attack 可以根据ip、域名等设置黑名单、设置访问频率 设置黑名单 # 新增 config/initializers/rack_attack.rb # 请求referer如果匹配不上设置的allowed_origins,返回403 forbidden Rack::Attack.blocklist(block bad domai…...
猫12分类:使用多线程爬取图片的Python程序
本文目标 对于猫12目标检测部分的数据集,采用网络爬虫来制作数据集。 在网络爬虫中,经常需要下载大量的图片。为了提高下载效率,可以使用多线程来并发地下载图片。本文将介绍如何使用Python编写一个多线程爬虫程序,用于爬取图片…...

《深度学习500问》外链笔记
1.这个是什么意思...

机器学习技术栈—— 概率学基础
机器学习技术栈—— 概率学基础 先验概率、后验概率、似然概率总体标准差和样本标准差 先验概率、后验概率、似然概率 首先 p ( w ∣ X ) p ( X ∣ w ) ∗ p ( w ) p ( X ) p(w|X) \frac{ p(X|w)*p(w)}{p(X)} p(w∣X)p(X)p(X∣w)∗p(w) 也就有 p ( w ∣ X ) ∝ p ( X ∣ …...
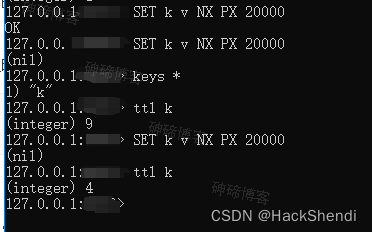
使用Redis实现分布式锁
Hi, I’m Shendi 使用Redis实现分布式锁 需求场景 需要使用到分布式锁的场景非常多,例如抢单等并发场景,这里举一个例子。 有一个商品,限量出售100个,一个用户下单,数量就减少一个,当剩下最后一个时&…...
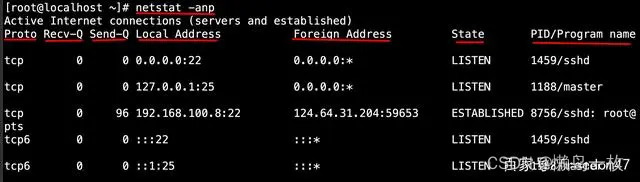
linux 服务器进程、端口查找,nginx 配置日志查找,lsof 命令详解
一 、根据端口号 查看文件的部署位置 1.1 使用查看端口号对应的进程信息 方式一 : 使用netstat命令 netstat -tuln | grep 端口号-t:显示TCP连接 -u:显示UDP连接 -l:仅显示监听状态的连接 -n:以数字形式显示端口…...
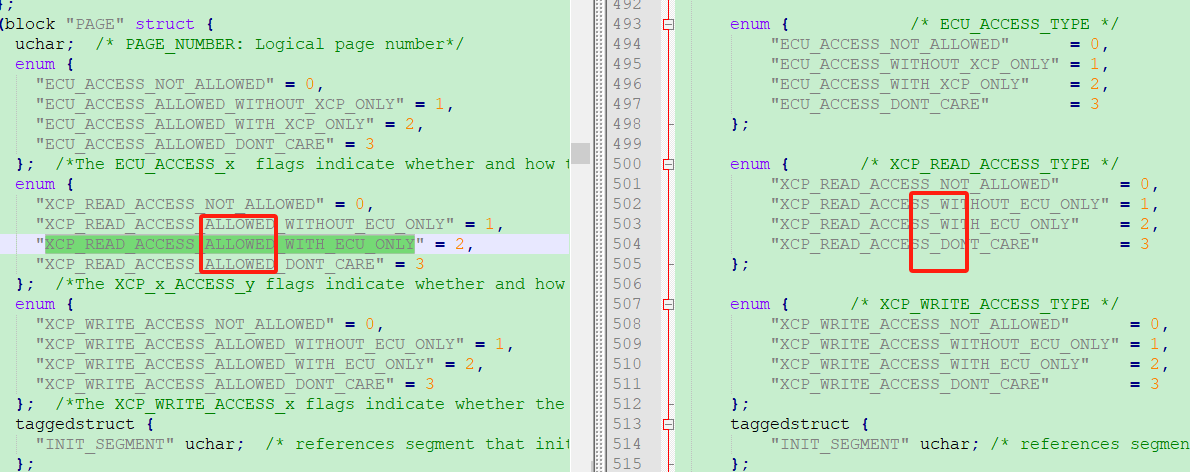
汽车标定技术--A2L格式分析
目录 1.A2L由来 2.A2L格式 2.1 PROJECT 2.2 MODULE中包含的内容 3. INCA和CANape兼容吗? 最近有朋友用Vector ASAP2Editor编译的A2L文件在INCA7.4中无法识别,我记得以前做的时候是可以识别的,难不成最近有什么变动吗?出于好…...

Linux操作系统使用及C高级编程-D9D10Linux 服务搭建与使用
TFTP服务器 TFTP(Trivial File Transfer Protocol)即简单文件传输协议,是TCP/IP协议中一个用来在客户机与服务器之间进行简单文件传输的协议,提供不复杂、开销不大的文件传输服务。端口号为69 1、使用客户服务器方式和使用UDP数据…...

git下载安装配置及Git在Gitee上拉取和上传代码教程
一、Git下载安装和配置 Git是一个分布式版本控制系统,用于跟踪文件的变化并协作开发。以下是安装和配置Git的简单步骤: 安装Git 下载Git安装程序:Git下载地址。 运行安装程序,按照提示进行安装。 在安装过程中,选择…...
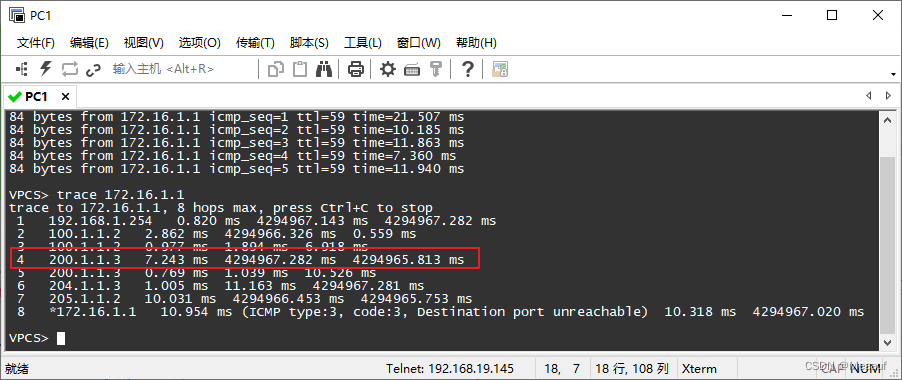
ospf路由选路及路由汇总
一、知识补充 1、ABR和ASBR 1.1 ABR ABR指的是边界路由,通常位于两个或多个区域之间,用于在不同的OSPF区域之间传递信息。当一个路由器同时连接到两个或多个区域时,它就成为了ABR,它需要维护每个区域的拓扑信息和路由表&#x…...

Oracle 11g 多数据库环境下的TDE设置
19c的TDE wallet的设置是在数据库中设置的,也就是粒度为数据库,因此不会有冲突。 而11g的设置是在sqlnet.ora中,因此有可能产生冲突。 这里先将一个重要概念,按照文档的说法,wallet是不能被数据库共享的。 If there …...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...
