机器学习技术栈—— 概率学基础
机器学习技术栈—— 概率学基础
- 先验概率、后验概率、似然概率
- 总体标准差和样本标准差
先验概率、后验概率、似然概率
首先
p ( w ∣ X ) = p ( X ∣ w ) ∗ p ( w ) p ( X ) p(w|X) =\frac{ p(X|w)*p(w)}{p(X)} p(w∣X)=p(X)p(X∣w)∗p(w)
也就有
p ( w ∣ X ) ∝ p ( X ∣ w ) ∗ p ( w ) p(w|X) \propto p(X|w)*p(w) p(w∣X)∝p(X∣w)∗p(w)
p ( w ) p(w) p(w)是先验(prior)概率,即先入为主,基于历史规律或经验,对事件 w w w做出概率为 p ( w ) p(w) p(w)的判断,而非基于客观事实。
p ( w ∣ X ) p(w|X) p(w∣X)是后验(posterior)概率,即马后炮,基于事实的校验,对事件 w w w做出一定条件下的概率判断。
p ( X ∣ w ) p(X|w) p(X∣w)是似然(likelihood)概率,似然,即似乎会这样,也就是事件 w w w发生时,发生 X X X的概率似乎是 p ( X ∣ w ) p(X|w) p(X∣w)这么大,是一个根据数据统计得到的概率,这一点性质和先验是一样的。
如何科学的马后炮得到后验概率呢?就要先依托历史规律,然后摆数据,历史规律+实事求是的数据就是科学的马后炮。后验概率,是在有数据后,对先验概率进行纠偏的概率。
| 参考文章 |
|---|
| Bayes’ Rule – Explained For Beginners |
| 《【辨析】先验概率、后验概率、似然概率》 |
总体标准差和样本标准差
样本标准差(sample standard deviation): S = ∑ ( X i − X ˉ ) 2 n − 1 S =\sqrt{ \frac{\sum(X_i - \bar X)^2}{n-1}} S=n−1∑(Xi−Xˉ)2
总体标准差(population standard deviation): σ = ∑ ( X i − X ˉ ) 2 n \sigma =\sqrt{ \frac{\sum(X_i - \bar X)^2}{n}} σ=n∑(Xi−Xˉ)2,population也有全体的意思
| 参考文章 |
|---|
| Standard_deviation - Wiki |
相关文章:

机器学习技术栈—— 概率学基础
机器学习技术栈—— 概率学基础 先验概率、后验概率、似然概率总体标准差和样本标准差 先验概率、后验概率、似然概率 首先 p ( w ∣ X ) p ( X ∣ w ) ∗ p ( w ) p ( X ) p(w|X) \frac{ p(X|w)*p(w)}{p(X)} p(w∣X)p(X)p(X∣w)∗p(w) 也就有 p ( w ∣ X ) ∝ p ( X ∣ …...
使用Redis实现分布式锁
Hi, I’m Shendi 使用Redis实现分布式锁 需求场景 需要使用到分布式锁的场景非常多,例如抢单等并发场景,这里举一个例子。 有一个商品,限量出售100个,一个用户下单,数量就减少一个,当剩下最后一个时&…...
linux 服务器进程、端口查找,nginx 配置日志查找,lsof 命令详解
一 、根据端口号 查看文件的部署位置 1.1 使用查看端口号对应的进程信息 方式一 : 使用netstat命令 netstat -tuln | grep 端口号-t:显示TCP连接 -u:显示UDP连接 -l:仅显示监听状态的连接 -n:以数字形式显示端口…...
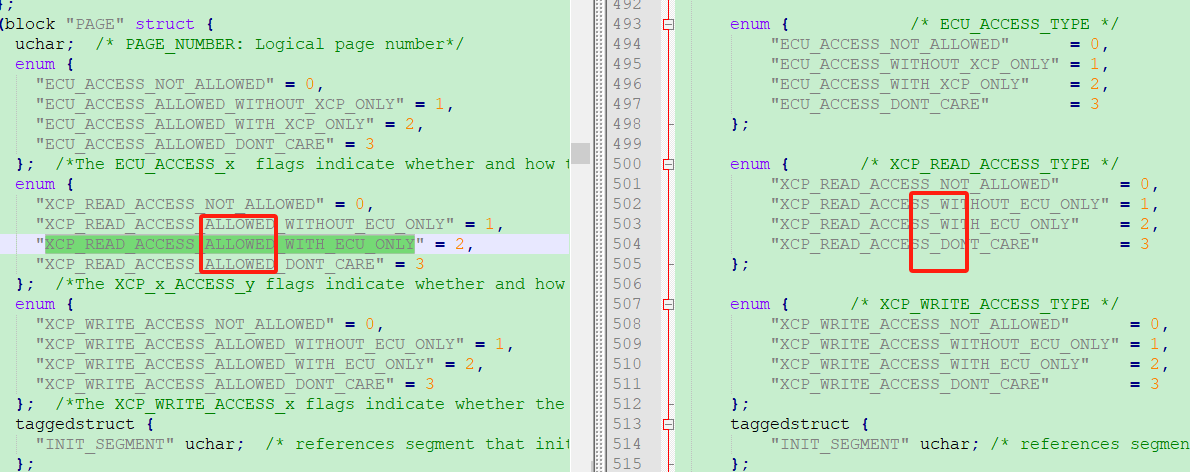
汽车标定技术--A2L格式分析
目录 1.A2L由来 2.A2L格式 2.1 PROJECT 2.2 MODULE中包含的内容 3. INCA和CANape兼容吗? 最近有朋友用Vector ASAP2Editor编译的A2L文件在INCA7.4中无法识别,我记得以前做的时候是可以识别的,难不成最近有什么变动吗?出于好…...

Linux操作系统使用及C高级编程-D9D10Linux 服务搭建与使用
TFTP服务器 TFTP(Trivial File Transfer Protocol)即简单文件传输协议,是TCP/IP协议中一个用来在客户机与服务器之间进行简单文件传输的协议,提供不复杂、开销不大的文件传输服务。端口号为69 1、使用客户服务器方式和使用UDP数据…...

git下载安装配置及Git在Gitee上拉取和上传代码教程
一、Git下载安装和配置 Git是一个分布式版本控制系统,用于跟踪文件的变化并协作开发。以下是安装和配置Git的简单步骤: 安装Git 下载Git安装程序:Git下载地址。 运行安装程序,按照提示进行安装。 在安装过程中,选择…...
ospf路由选路及路由汇总
一、知识补充 1、ABR和ASBR 1.1 ABR ABR指的是边界路由,通常位于两个或多个区域之间,用于在不同的OSPF区域之间传递信息。当一个路由器同时连接到两个或多个区域时,它就成为了ABR,它需要维护每个区域的拓扑信息和路由表&#x…...

Oracle 11g 多数据库环境下的TDE设置
19c的TDE wallet的设置是在数据库中设置的,也就是粒度为数据库,因此不会有冲突。 而11g的设置是在sqlnet.ora中,因此有可能产生冲突。 这里先将一个重要概念,按照文档的说法,wallet是不能被数据库共享的。 If there …...

vue3使用pinia实现数据缓存
文章目录 前言一、pinia是什么?二、安装pinia三、注册pinia四、使用pinia定义数据及方法使用 优化如有启发,可点赞收藏哟~ 前言 vue2以前一直使用vuex实现状态管理 vue3之后推出了pinia… 一、pinia是什么? 直观、类型安全、轻便灵活的Vue …...
)
【CSS】min 和 max 函数(设置最大最小值)
文章目录 min() 函数:允许你从逗号分隔符表达式中选择一个最小值作为 CSS 的属性值 width: min(1vw, 4em, 80px);max() 函数:让你可以从一个逗号分隔的表达式列表中选择最大(正方向)的值作为属性的值 width: max(10vw, 4em, 80p…...

ip地址跟wifi有关系吗
你可能已经听说过IP地址和Wi-Fi这两个词,但你有没有想过它们之间是否有关系呢?在这篇文章中,我们将深入探讨IP地址与Wi-Fi之间的密切联系。从基本概念到应用实例,虎观代理小二二将为您解答这个问题。 首先,让我们来了…...
[算法学习笔记](超全)概率与期望
引子 先来讲个故事 话说在神奇的OI大陆上,有一只paper mouse 有一天,它去商场购物,正好是11.11,商店有活动 它很荣幸被选上给1832抽奖 在抽奖箱里,有3个篮蓝球,12个红球 paper mouse能抽3次 蒟蒻的p…...

SpringCloud相关
文章目录 Gateway动态路由灰度策略 FeignRibbon SpringCloud五大组件分别对应(1)服务注册与发现(2)客服端负载均衡(3)断路器(4)服务网关(5)分布式配置 Gatewa…...

在 Linux 和 Windows 系统下查看 CUDA 和 cuDNN 版本的方法,包括使用 nvcc 命令
一直都比较头疼cuda与cudnn版本查看问题,两个系统不一样也不好查看,命令不通用 Linux 查看 CUDA 版本 方法一: nvcc --version或 nvcc -V如果 nvcc 没有安装,那么用方法二。 方法二: 去安装目录下查看ÿ…...
idea项目中java类名出现带 j 小红点,如何解决?
目录 一、问题描述 二、问题解决方案 1、寻找异常问题 2、解决方案 2.1常规操作方法 2.2 快速操作方法 一、问题描述 一打开idea的java项目,发现所有的文件边上都有带J的大红点 虽然,在 git bash 中进行编译时无异常。 但是视觉上给人的感受就是…...
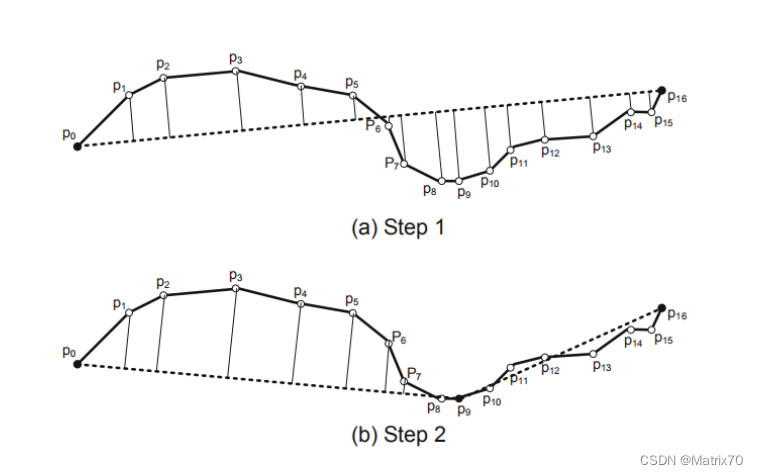
生产环境_移动目标轨迹压缩应用和算法处理-Douglas-Peucker轨迹压缩算法
场景: 我目前设计到的场景是:即在地图应用中,对GPS轨迹数据进行压缩,减少数据传输和存储开销,因为轨迹点太频繁了,占用空间太大,运行节点太慢了,经过小组讨论需要上这个算法&#x…...
HINSTANCE是什么?
HINSTANCE 就是 HMODULE:...

uniapp小程序定位;解决调试可以,发布不行的问题
遇见这个问题;一般情况就两种 1、域名配置问题; 2、隐私协议问题 当然,如果你的微信小程序定位接口没开启;定位也会有问题; 第一种,小程序一般是腾讯地图;所以一般都会用https://apis.map.qq.co…...

C++学习 --pair
目录 1, 什么是pair 2, 创建pair 2-1, 标准数据类型 2-2, 自定义数据类型 3, 查询元素 3-1, 标准数据类型 3-2, 自定义数据类型 1, 什么是pair 数据以键值对形式存放的容器&…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

