当前位置：首页 > news >正文

[算法学习笔记](超全)概率与期望

news 2025/12/16 0:19:34

引子

先来讲个故事······

话说在神奇的OI大陆上，有一只paper mouse

有一天，它去商场购物，正好是11.11，商店有活动

它很荣幸被选上给1832抽奖

在抽奖箱里，有3个篮蓝球，12个红球

paper mouse能抽3次

蒟蒻的paper mouse就疑惑了:抽到至少1个篮蓝球的概率是多少？？？

Answer:

总共有15个球

只抽到1个篮蓝球的概率是 $\frac{C_{3}^{1}*C_{12}^{2}}{C_{15}^{3}}$ $\approx$ 0.435165（很好理解吧，在4个篮蓝球里取一个，再在11个红球里面取3个，总共是在15个里面取4个）

抽到2个篮蓝球的概率是 $\frac{C_{3}^{2}*C_{12}^{1}}{C_{15}^{3}}$ $\approx$ 0.079121

抽到3个篮蓝球的概率是 $\frac{C_{3}^{3}*C_{12}^{0}}{C_{15}^{3}}$ $\approx$ 0.002198

所以总概率就是三者之和，即0.435165+0.079121+0.002198=0.516484 $\approx$ $\frac{129}{250}$

我们也可以反过来分析：如果paper mouse运气爆棚，一个篮蓝球都没有抽到

那么其对立事件就一定会有至少一个篮蓝球

所以概率就是:1- $\frac{C_{12}^{3}}{C_{15}^{3}}$ $\approx$ 1-0.483516=0.516484 $\approx$ $\frac{129}{250}$

也就是说，paper mouse有接近 $\frac{1}{2}$ 的概率给心爱的1832送上礼物······

概率

概率就是随机事件出现的可能性大小

For example，上面的故事里就涉及到概率

若某种事件重复了N次，其中A事件出现了M次，出现A事件的概率就是 $\frac{M}{N}$

同时， $0\leq \frac{M}{N}\leq 1$ ，用 $P()$ 表示

即： $P(A)=\frac{M}{N}$

1.1 条件概率与全概率

条件概率公式：

如果事件A发生的概率为P(A)，事件B单独发生的概率为P(b)

若B必须在A发生之后发生，则B发生的概率就是条件概率，P(B)=P(A|b)= $\frac{P(AB)}{P(b)}$

（是不是还比较好理解？真正shit的才刚刚开始）

全概率公式：

如果事件 B1, B2,⋯, Bn 构成一个完整的样本空间，且两两互斥，P(Bi) > 0。则对于任意事件 A 有： $P(A)=\sum_{i=1}^{n}P(A|B_i)P(B_i)$ ，这就是全概率公式

思想就是：P(A)不是很好求，但是把P(A)拆开计算P(A|Bi)P(Bi)就相对好算一些

举个例子：

paper mouse去表白1832了
他每次写情书，1832都有0.5的概率看见
而第一次看见，1832有0.2的概率同意他
第二次看见时，1832有0.5的概率同意他
第三次看见时，1832一定会同意他的请求

求paper mouse获得1832爱情的概率

通过全概率公式：

事件A是paper mouse陷入爱河

事件集合B是：B={ $B_0,B_1,B_2,B_3$ }， $B_i$ 表示paper mouse表白了i次

$P(A)=P(AB_0)+P(AB_1)+P(AB_2)+P(AB_3)$

$= P(A|B_0)P(B_0) + P(A|B_1)P(B_1) + P(A|B_2)P(B_2)+ P(A|B_3)P(B_3)$

$=0+C_{3}^{1}*0.5^{3}*0.2+C_{3}^{2}*0.5^{3}*0.5+C_{3}^{3}*0.5^{3}*1$

$=0.3875$

所以paper mouse表白成功的概率高达0.3！（喜）

期望

炸裂的东西来了

先看看期望的定义

1.1 期望定义

如果随机变量只取得有限个值或无穷能按一定次序一一列出，其值域为一个或若干个有限或无限区间，这样的随机变量称为离散型随机变量。

离散型随机变量的一切可能的取值 Xi 与对应的概率 P(Xi) 乘积之和称为该离散型随机变量的数学期望，记为 E(X) ，简称期望。

~~怎么样？是不是蛮有意思的？~~

换一种通俗但不精确的方式阐述一下（涉及下定义内容，非xxs请谨慎观看）：

期望就是某件事发生的概率集合中的每一个数对其对应值的乘积的和

一个普通骰子，众所周知有六面，对应1~6

每一面转到的概率就是 $\frac{1}{6}$ ，所以：

$E(X)=\frac{1}{6}*1+\frac{1}{6}*2+\frac{1}{6}*3+\frac{1}{6}*4+\frac{1}{6}*5+\frac{1}{6}*6$

$=\frac{1}{6}*(1+2+3+4+5+6)$

$=3.5$

所以也可以这么说：

数学期望可以理解为某件事情大量发生之后的平均结果。

来个难点的：

设一张彩票为 2 元，每售 100000 张开奖，假每张彩票有一个对应的六位数号码，奖次如下：

安慰奖：奖励 4 元，中奖概率0.1
幸运奖：奖励 20 元，中奖概率 0.01
手气奖：奖励 200 元，中奖概率 0.001
一等奖：奖励 2000 元，中奖概率 0.0001
特等奖：奖励 20000 元，中奖概率 0.00001

那公司到底是亏还是赚呢？

我们来简单计算一下，对于每一位购买彩票的用户，公司可能支出为：

$0.14+0.01*20+0.001*200+0.0001*2000+0.00001*20000=1.2$

所以公司期望赚0.8元

1.2 期望的线性性质

设 X, Y 是任意两个随机变量，则有

E(X + Y ) = E(X) + E(Y )
E(aX + bY ) = aE(X) + bE(Y )

证明略

再举个栗子：

同时仍一颗骰子的期望为3.5

同时扔两颗骰子的概率是3.5+3.5=7

1.3 条件期望与全期望公式

一个经典xxs的题：

A班平均分为x分，B班平均分为y分

求A、B两个班的平均分

显而易见的：A、B班的平均分不能直接(x+y)/2

而是： $(x*a+ y*b)/(x+y)$ ，其中a表示A班人数，b表示B班人数

期望也差不多。

友好的看一下全期望公式：

设 X 是一个离散型随机变量，当 X = xi 时，随机变量 Y 可能包含多种情况 y1, y2,⋯, yk，随机变量 Y 的条件数学期望为：

$E(Y|X=x_i)=\sum ^{k}_{j=1}y_j × P(Y = y_j |X = x_i)$

对于随机变量 X 有很多取值 x1, x2,⋯, xa，Y 有很多取值 y1, y2,⋯, yb。

全期望公式：

$E(Y)=E(E(Y|X))$

   $=\sum ^{a}_{i=1}P(X = x_i)E(Y|X = x_i)$

   $= \sum^{a}_{i=1}P(X=x_i)\sum^{b}_{j=1}y_j*P(Y=y_j|X=x_i)$

   $=\sum^{a}_{i=1}\sum^{b}_{j=1}y_j*P(X=xi)*P(Y= y_i|X=x_i)$

   $=\sum^{a}_{i=1}\sum^{b}_{j=1}y_j×P(X=x_i,Y=y_j)$

   $=E(Y)$

例如，一项工作由甲一个人完成，平均需要 4 小时，而乙有 0.4 的概率来帮忙，两个人完成平均只需要 3 小时。

若用 X 表示完成这项工作的人数，而 Y 表示完成的这项工作的期望时间（单位小时）

由于这项工作要么由一个人完成，要么由两个人完成，那么这项工作完成的期望时间

$E(Y)=P(X=1)*E(Y|X=1)+P(X=2)*E(Y|X=2)=(1-0.4)*4-0.4*3=3.6$

(例题下次更新)

[算法学习笔记](超全)概率与期望

引子先来讲个故事话说在神奇的OI大陆上，有一只paper mouse 有一天，它去商场购物，正好是11.11，商店有活动它很荣幸被选上给1832抽奖在抽奖箱里，有3个篮蓝球，12个红球 paper mouse能抽3次蒟蒻的p…...

编程日记 2023/11/21 13:08:53

SpringCloud相关

文章目录 Gateway动态路由灰度策略 FeignRibbon SpringCloud五大组件分别对应（1）服务注册与发现（2）客服端负载均衡（3）断路器（4）服务网关（5）分布式配置 Gatewa…...

编程日记 2023/11/21 13:07:52

在 Linux 和 Windows 系统下查看 CUDA 和 cuDNN 版本的方法，包括使用 nvcc 命令

一直都比较头疼cuda与cudnn版本查看问题，两个系统不一样也不好查看，命令不通用 Linux 查看 CUDA 版本方法一： nvcc --version或 nvcc -V如果 nvcc 没有安装，那么用方法二。方法二： 去安装目录下查看&#xff…...

编程日记 2023/11/21 13:05:50

4.10每日一题（二元函数极值相关重要性质，反复学习）

...

编程日记 2023/11/21 13:04:49

idea项目中java类名出现带 j 小红点，如何解决？

目录一、问题描述二、问题解决方案 1、寻找异常问题 2、解决方案 2.1常规操作方法 2.2 快速操作方法一、问题描述一打开idea的java项目，发现所有的文件边上都有带J的大红点虽然，在 git bash 中进行编译时无异常。但是视觉上给人的感受就是…...

编程日记 2023/11/21 13:02:46

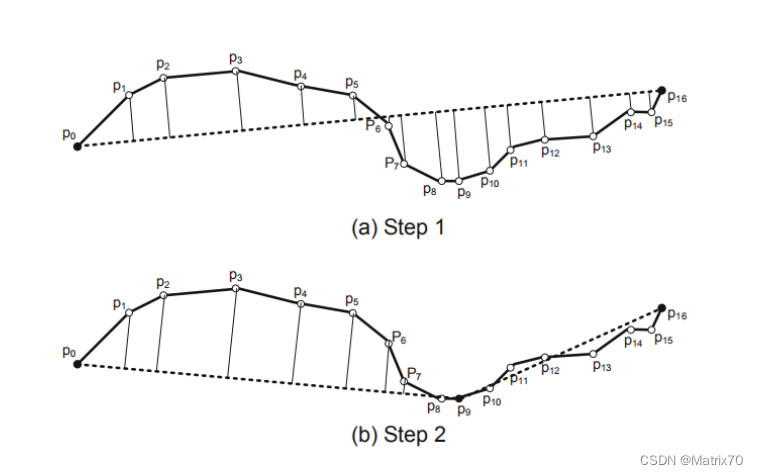
生产环境_移动目标轨迹压缩应用和算法处理-Douglas-Peucker轨迹压缩算法

场景： 我目前设计到的场景是：即在地图应用中，对GPS轨迹数据进行压缩，减少数据传输和存储开销，因为轨迹点太频繁了，占用空间太大，运行节点太慢了，经过小组讨论需要上这个算法&#x…...

编程日记 2023/11/21 13:01:45

HINSTANCE是什么？

HINSTANCE 就是 HMODULE：...

编程日记 2023/11/21 13:00:42

uniapp小程序定位；解决调试可以，发布不行的问题

遇见这个问题；一般情况就两种 1、域名配置问题； 2、隐私协议问题当然，如果你的微信小程序定位接口没开启；定位也会有问题； 第一种，小程序一般是腾讯地图；所以一般都会用https://apis.map.qq.co…...

编程日记 2023/11/21 12:59:41

C++学习 --pair

目录 1， 什么是pair 2， 创建pair 2-1， 标准数据类型 2-2， 自定义数据类型 3， 查询元素 3-1， 标准数据类型 3-2， 自定义数据类型 1， 什么是pair 数据以键值对形式存放的容器&…...

编程日记 2023/11/21 12:58:40

Android Frgment中onActivityResult无效的问题

前言最近在fragment中使用二维码扫描发现拿不到onActivityResult返回查了资料说是启动模式或者是返回值为负数断点调试发现根本没走onActivityResult方法问题 onActivityResult 在附属Activity中被拦截了所以没有触发该方法解决在Fragment所依赖的Activity中执…...

编程日记 2023/11/21 12:57:39

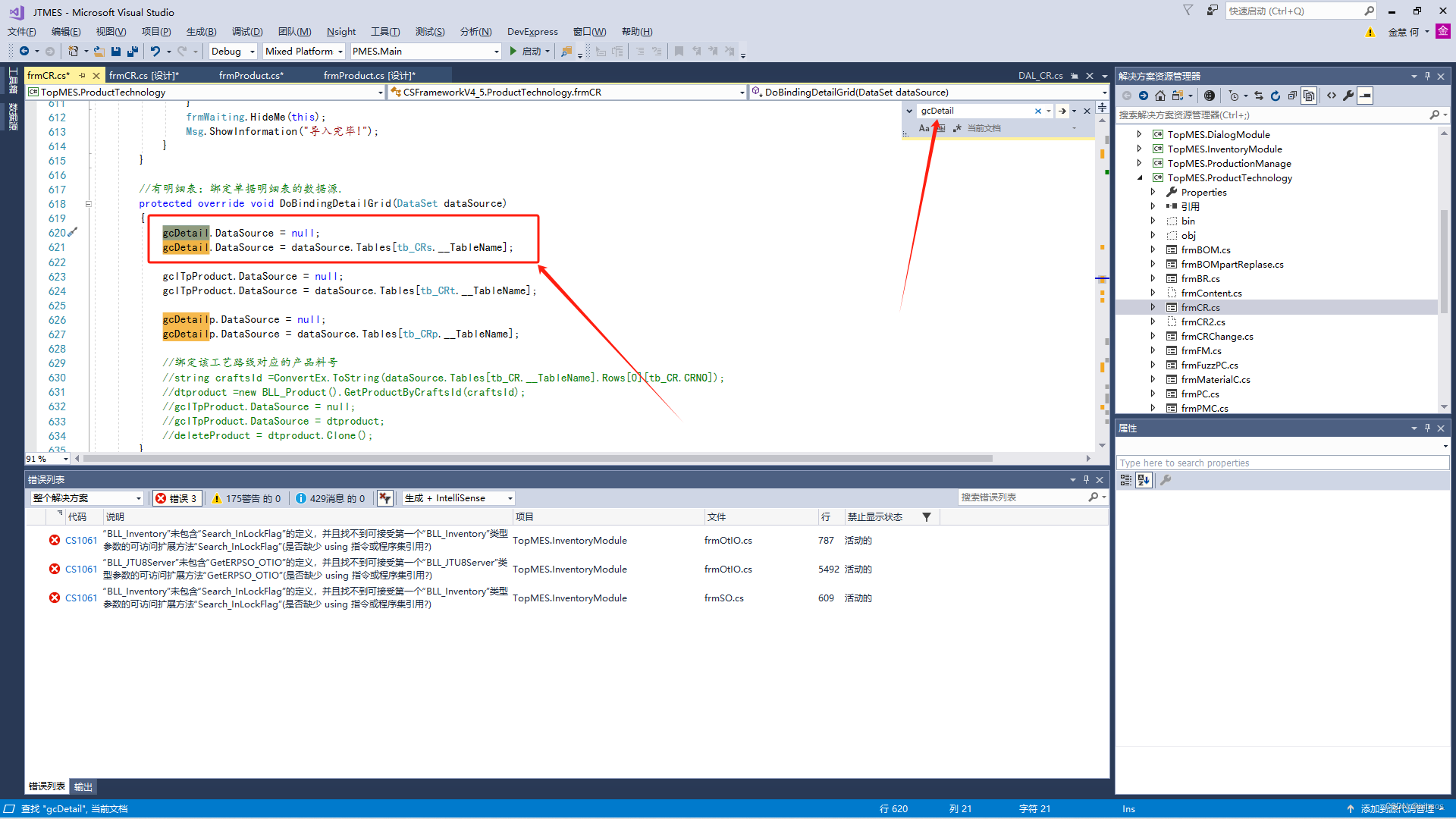
【C#二开业务冠邑】通过界面查看数据来源

前言重构框架（CS【C#】转BS【Java】）时，突然发现公司的代码和数据库，有部分都没有写注释，嘎嘎，这不非常影响开发效率，于是乎，开始帮公司整理表结构和数据来源，也从而加…...

编程日记 2023/11/21 12:56:39

使用大语言模型 LLM 做文本分析

本文主要分享传统聚类算法 LLM与嵌入算法嵌入算法聚类 LLM的其他用法聚类是一种无监督机器学习技术，旨在根据相似的数据点的特征将其分组在一起。使用聚类成簇，有助于解决各种问题，例如客户细分、异常检测和文本分类等。尽管传统的聚…...

编程日记 2023/11/21 12:55:38

Windows本地搭建rtmp推流服务

前言开发时偶尔需要使用rtmp直播流做视频流测试，苦于网上开源的rtmp视频流都已经失效，无奈只好尝试在本地自己搭建一个rtmp的推流服务，方便测试使用。一、工具准备 Nginx：使用nginx-rtmp-win64推流工具FFmpeg：官方…...

编程日记 2023/11/21 12:54:37

机器学习二元分类二元交叉熵二元分类例子

二元交叉熵损失函数深度学习中的二元分类损失函数通常采用二元交叉熵（Binary Cross-Entropy）作为损失函数。二元交叉熵损失函数的基本公式是： L(y, y_pred) -y * log(y_pred) - (1 - y) * log(1 - y_pred)其中，y是真实标签&…...

编程日记 2023/11/21 12:52:35

Postgresql运维信息(一)

1. 运维系统视图 PostgreSQL 提供了一系列系统视图和函数，可以用于获取数据库的运维统计信息。这些信息对于监控和优化数据库性能非常有用。以下是一些常用的 PostgreSQL 运维统计信息： 1.1. pg_stat_activity 这个系统视图包含了当前数据库连接的活动…...

编程日记 2023/11/21 12:51:34

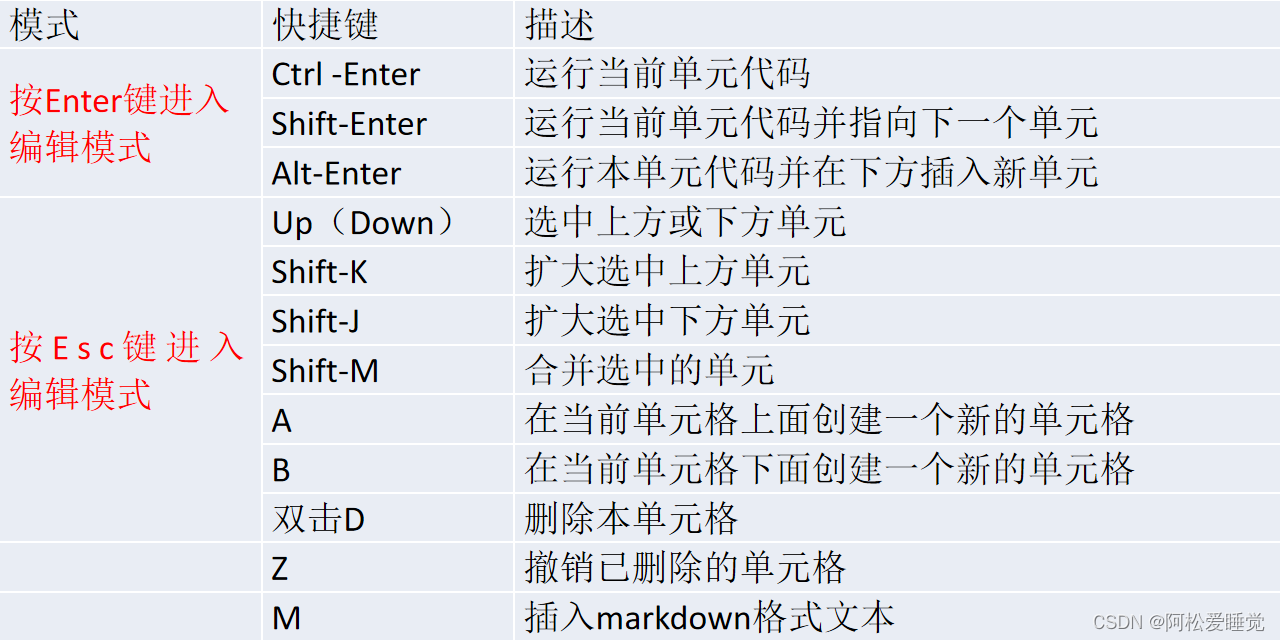
Jupyter Notebook的下载安装与使用教程_Python数据分析与可视化

Jupyter Notebook的下载安装与使用 Jupyter简介下载与安装启动与创建NotebookJupyter基本操作在计算机编程领域，有一个很强大的工具叫做Jupyter。它不仅是一个集成的开发环境，还是一个交互式文档平台。对于初学者来说，Jupyter提供了友好的界…...

编程日记 2023/11/21 12:50:33

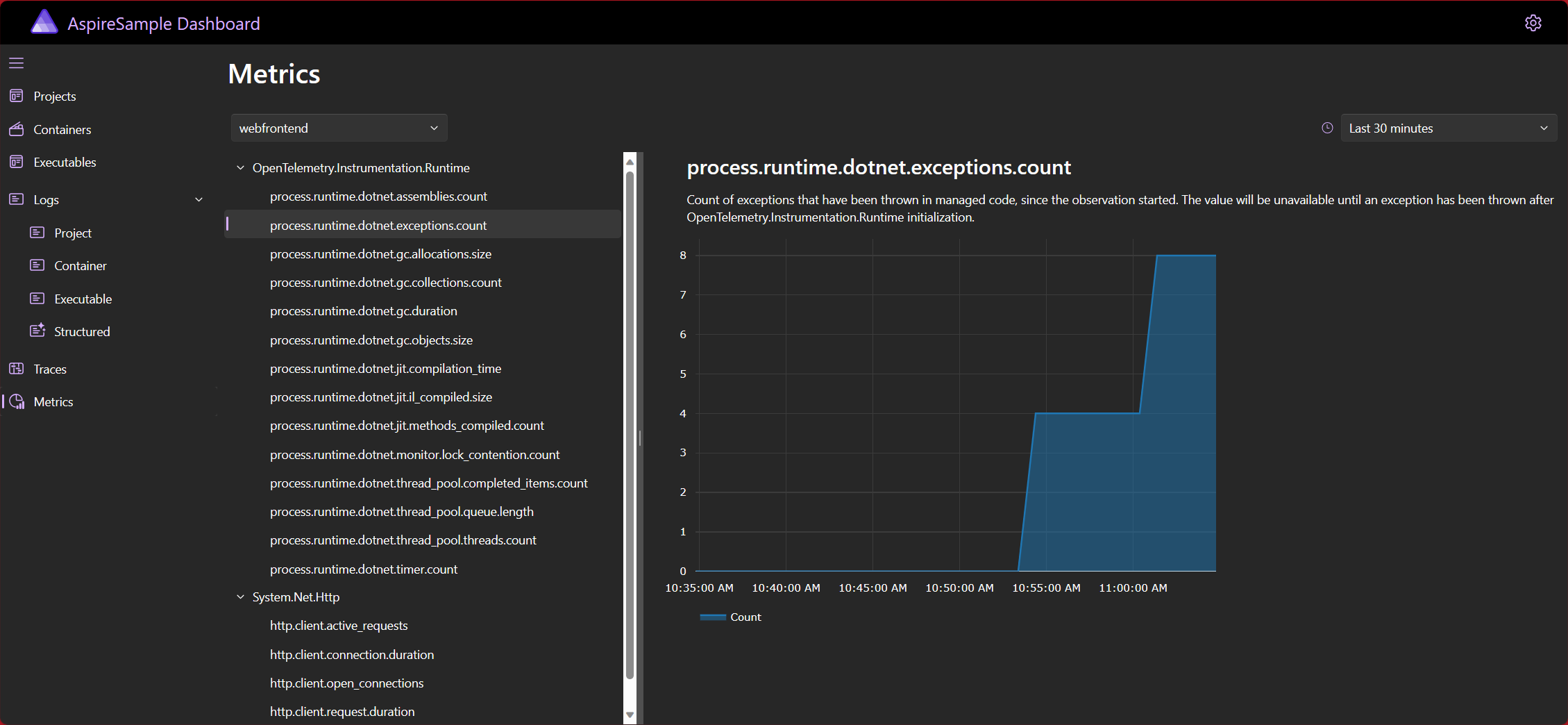
快速入门：构建您的第一个 .NET Aspire 应用程序

##前言云原生应用程序通常需要连接到各种服务，例如数据库、存储和缓存解决方案、消息传递提供商或其他 Web 服务。.NET Aspire 旨在简化这些类型服务之间的连接和配置。在本快速入门中，您将了解如何创建 .NET Aspire Starter 应用程序模板解决方案。 …...

编程日记 2023/11/21 12:49:29

主流开源大语言模型的微调方法

文章目录模型ChatGLM2网址原生支持微调方式 ChatGLM3网址原生支持微调方式 Baichuan 2网址原生支持微调方式 Qwen网址原生支持微调方式框架FireflyEfficient-Tuning-LLMsSuperAdapters 模型 ChatGLM2 网址 https://github.com/thudm/chatglm2-6b 原生支持微调方式 https…...

编程日记 2023/11/21 12:48:29

Django DRF权限组件

在Django的drf框架内的权限组件，如果遇到多个权限认证类，是需要所有的权限类都要通过验证，才能访问视图。一、简单示例 1、per.py 自定义权限类 from rest_framework.permissions import BasePermission import randomclass MyPerssion(B…...

编程日记 2023/11/21 12:47:28

leetcode每日一题31

搜索旋转排序数组那……二分法呗数组中的数可以相同比 33. 搜索旋转排序数组多了一个「有重复元素」，导致无法根据 num > nums[0] 来判断 num 在哪一半，比如 [1,1,1,1,1,2,1,1,1] 旋转数组两头相等，元素 1 可能在左半边可能在右半边 …...

编程日记 2023/11/21 12:46:26

浅谈 React Hooks

React Hooks 是 React 16.8 引入的一组 API，用于在函数组件中使用 state 和其他 React 特性（例如生命周期方法、context 等）。Hooks 通过简洁的函数接口，解决了状态与 UI 的高度解耦，通过函数式编程范式实现更灵活 Rea…...

编程新知 2025/9/23 15:13:40

Cursor实现用excel数据填充word模版的方法

cursor主页：https://www.cursor.com/ 任务目标：把excel格式的数据里的单元格，按照某一个固定模版填充到word中文章目录注意事项逐步生成程序1. 确定格式2. 调试程序注意事项直接给一个excel文件和最终呈现的word文件的示例，…...

编程新知 2025/8/23 5:46:26

Flask RESTful 示例

目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务中文乱码问题： 下面创建一个简单的Flask RESTful API示例。首先，我们需要创建环境，安装必要的依赖，然后…...

编程新知 2025/12/15 19:58:03

stm32G473的flash模式是单bank还是双bank？

今天突然有人stm32G473的flash模式是单bank还是双bank？由于时间太久，我真忘记了。搜搜发现，还真有人和我一样。见下面的链接：https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

编程新知 2025/12/9 1:55:05

智慧工地云平台源码，基于微服务架构+Java+Spring Cloud +UniApp +MySql

智慧工地管理云平台系统，智慧工地全套源码，java版智慧工地源码，支持PC端、大屏端、移动端。智慧工地聚焦建筑行业的市场需求，提供“平台网络终端”的整体解决方案，提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

编程新知 2025/12/13 13:27:37

微信小程序 - 手机震动

一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码注：文档 https://developers.weixin.qq…...

编程新知 2025/12/15 8:43:18

QT3D学习笔记——圆台、圆锥

类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体（对象或容器）QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质（定义颜色、反光等）QFirstPersonC…...

编程新知 2025/9/22 1:53:57