LeetCode 0053. 最大子数组和:DP 或 递归(线段树入门题?)
【LetMeFly】53.最大子数组和:DP 或 递归
力扣题目链接:https://leetcode.cn/problems/maximum-subarray/
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
方法一:DP
使用动态规划的话思路比较简单,使用一个变量 c n t cnt cnt记录以当前元素为结尾的最大子数组和。
这样,我们只需要遍历一遍 n u m s nums nums数组,使用公式 c n t = max ( c n t + n u m s [ i ] , n u m s [ i ] ) cnt = \max(cnt + nums[i], nums[i]) cnt=max(cnt+nums[i],nums[i])维护 c n t cnt cnt,并记得更新答案的最大值即可。
- 时间复杂度 O ( l e n ( n u m s ) ) O(len(nums)) O(len(nums))
- 空间复杂度 O ( 1 ) O(1) O(1)
AC代码
C++
class Solution {
public:int maxSubArray(vector<int>& nums) {int ans = nums[0];int cnt = nums[0];for (int i = 1; i < nums.size(); i++) {cnt = max(cnt + nums[i], nums[i]);ans = max(ans, cnt);}return ans;}
};
Python
# from typing import Listclass Solution:def maxSubArray(self, nums: List[int]) -> int:ans, cnt = nums[0], nums[0]for i in range(1, len(nums)):cnt = max(cnt + nums[i], nums[i])ans = max(ans, cnt)return ans
方法二:递归(分治)
写一个函数 g e t ( n u m s , l , r ) get(nums, l, r) get(nums,l,r),返回 n u m s nums nums数组从 l l l到 r r r的子数组的:
- lSum: 以 n u m s [ l ] nums[l] nums[l]为起点的
最大子数组和 - rSum: 以 n u m s [ r ] nums[r] nums[r]为终点的
最大子数组和 - MSum:
最大子数组和 - iSum: 和
那么,我们就可以愉快地进行递归啦!
对于 g e t ( n u m s , l , r ) get(nums, l, r) get(nums,l,r),我们可以分别求出 g e t ( n u m s , l , ⌊ l + r 2 ⌋ ) get(nums, l, \lfloor\frac{l + r}{2}\rfloor) get(nums,l,⌊2l+r⌋)(记为 l S t a t u s lStatus lStatus)和 g e t ( n u m s , ⌊ l + r 2 ⌋ + 1 , r ) get(nums, \lfloor\frac{l + r}{2}\rfloor + 1, r) get(nums,⌊2l+r⌋+1,r)(记为 r S t a t u s rStatus rStatus)。递归终止条件为 l = r l=r l=r(只有单个元素)。
于是就有:
- l S u m = max ( l S t a t u s . l S u m , l S t a t u s . i S u m + r S t a t u s . l S u m ) lSum = \max(lStatus.lSum, lStatus.iSum + rStatus.lSum) lSum=max(lStatus.lSum,lStatus.iSum+rStatus.lSum)(以 n u m s [ l ] nums[l] nums[l]为起点,不跨过 n u m s [ ⌊ l + r 2 ⌋ ] nums[\lfloor\frac{l + r}{2}\rfloor] nums[⌊2l+r⌋]和跨过)
- r S u m = max ( r S t a t u s . r S u m , l S t a t u s . r S u m + r S t a t u s . i S u m ) rSum = \max(rStatus.rSum, lStatus.rSum + rStatus.iSum) rSum=max(rStatus.rSum,lStatus.rSum+rStatus.iSum)(以 n u m s [ r ] nums[r] nums[r]为终点,不跨过 n u m s [ ⌊ l + r 2 ⌋ ] nums[\lfloor\frac{l + r}{2}\rfloor] nums[⌊2l+r⌋]和跨过)
- M S u m = max ( l S t a t u s . M S u m , r S t a t u s . M S u m , l S t a t u s . r S u m + r S t a t u s . l S u m ) MSum = \max(lStatus.MSum, rStatus.MSum, lStatus.rSum + rStatus.lSum) MSum=max(lStatus.MSum,rStatus.MSum,lStatus.rSum+rStatus.lSum)(左半部分最大子数组和、右半部分最大子数组和、跨过 n u m s [ ⌊ l + r 2 ⌋ ] nums[\lfloor\frac{l + r}{2}\rfloor] nums[⌊2l+r⌋]的子数组和)
- i S u m = l S t a t u s . i S u m + r S t a t u s . i S u m iSum = lStatus.iSum + rStatus.iSum iSum=lStatus.iSum+rStatus.iSum(左半右半数组和 之和)
最终返回 g e t ( n u m s , 0 , l e n ( n u m s ) − 1 ) . M S u m get(nums, 0, len(nums) - 1).MSum get(nums,0,len(nums)−1).MSum即可。
- 时间复杂度 O ( l e n ( n u m s ) ) O(len(nums)) O(len(nums))(相当于后序遍历了一遍二叉树)
- 空间复杂度 O ( log l e n ( n u m s ) ) O(\log len(nums)) O(loglen(nums))(空间复杂度主要来源于递归)
AC代码
C++
struct Status {int lSum, rSum, MSum, iSum;
};class Solution {
private:Status get(vector<int>& a, int l, int r) { // get[l, r]if (l == r) {return {a[l], a[l], a[l], a[l]};}int m = (l + r) >> 1;Status lStatus = get(a, l, m);Status rStatus = get(a, m + 1, r);return {max(lStatus.lSum, lStatus.iSum + rStatus.lSum),max(rStatus.rSum, lStatus.rSum + rStatus.iSum),max(lStatus.MSum, max(rStatus.MSum, lStatus.rSum + rStatus.lSum)),lStatus.iSum + rStatus.iSum};}
public:int maxSubArray(vector<int>& nums) {return get(nums, 0, nums.size() - 1).MSum;}
};
Python
# from typing import Listclass Status:def __init__(self, lSum: int, rSum: int, MSum: int, iSum: int) -> None:self.lSum = lSumself.rSum = rSumself.MSum = MSumself.iSum = iSumclass Solution:def get(self, nums: List[int], l: int, r: int) -> Status:if l == r:return Status(nums[l], nums[l], nums[l], nums[l])m = (l + r) >> 1lStatus = self.get(nums, l, m)rStatus = self.get(nums, m + 1, r)return Status(max(lStatus.lSum, lStatus.iSum + rStatus.lSum),max(rStatus.rSum, lStatus.rSum + rStatus.iSum),max(lStatus.MSum, rStatus.MSum, lStatus.rSum + rStatus.lSum),lStatus.iSum + rStatus.iSum)def maxSubArray(self, nums: List[int]) -> int:return self.get(nums, 0, len(nums) - 1).MSum"""为何不用切片作为参数?
>>> a = [1, 2, 3]
>>> a
[1, 2, 3]
>>> b = a[1:2]
>>> b
[2]
>>> b[0] = 99
>>> a
[1, 2, 3]
>>> b
[99]
"""
方法二意义何在?
相较于方法一,方法二的时间复杂度没有提升,空间复杂度反而更高了。那么方法二的意义何在?
这道题只问了“整个数组的”最大子数组和。但是如果某天遇到了一道题,问你 1 0 5 10^5 105次且每次随机问一个 [ l , r ] [l, r] [l,r]的最大子数组和 呢?
那么我们使用方法二,并且将每层的结果记录下来,就能做到每次查询都在 O ( log n ) O(\log n) O(logn)的时间复杂度下返回结果。
这就是没有懒标记的线段树。
同步发文于CSDN,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/134504375
相关文章:
)
LeetCode 0053. 最大子数组和:DP 或 递归(线段树入门题?)
【LetMeFly】53.最大子数组和:DP 或 递归 力扣题目链接:https://leetcode.cn/problems/maximum-subarray/ 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最…...

二十三种设计模式全面解析-解密职责链模式:请求处理的设计艺术
当我们构建软件系统时,经常会遇到需要处理各种不同类型请求的情况。有时,请求的处理逻辑可能相当复杂,需要按照一定的规则和条件进行处理。在本文中,我们将深入探讨职责链模式在请求处理中的应用。职责链模式通过将请求发送者和接…...

【linux】安装telnet
Telnet Telnet协议是TCP/IP协议族中的一员,是Internet远程登录服务的标准协议和主要方式。它为用户提供了在本地计算机上完成远程主机工作的能力。在终端使用者的电脑上使用telnet程序,用它连接到服务器。终端使用者可以在telnet程序中输入命令…...

深入探索 PaddlePaddle 中的计算图
**引言** 计算图是深度学习平台 PaddlePaddle 的核心组件之一,它提供了一种图形化的方式来表示和执行深度学习模型。通过了解和理解 PaddlePaddle 中的计算图,我们可以更好地理解深度学习的工作原理,并且能够更加灵活和高效地构建和训练复杂…...

西南科技大学814考研一
C语言基础 字节大小 char:1 字节 unsigned char:1 字节 short:2 字节 unsigned short:2 字节 int:通常为 4 字节(32 位平台)或 8 字节(64 位平台) unsigned int&#x…...

【网络编程】简述TCP通信程序,三次握手,四次挥手
文章目录 🎄TCP通信程序⭐打印字符串✨中文乱码问题🎈解决方法 🌺TCP三次握手🌺TCP四次挥手🛸其他 🎊专栏【网络编程】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆…...
 使用介绍 5 -- Trace32 ELF 文件加载介绍】)
【ARM Trace32(劳特巴赫) 使用介绍 5 -- Trace32 ELF 文件加载介绍】
请阅读【ARM Coresight SoC-400/SoC-600 专栏导读】 文章目录 1.1 Trace32 加载符号表1.1.1 ELF 文件加载1.1.2 其它格式文件加载1.1.3 多个 ELF 的加载1.2 Trace32 UEFI 配置1.2.1 x86 32-BIT1.2.2 x86 64-BIT1.2.3 ARM1.1 Trace32 加载符号表 劳特巴赫 TRACE32 可以显示目标…...
Linux(4):Linux文件与目录管理
目录与路径 相对路径在进行软件或软件安装时非常有用,更加方便。利用相对路径的写法必须要确认目前的路径才能正确的去到想要去的目录。 绝对路径的正确度要比相对路径好,因此,在写程序(shell scripts)来管理系统的条…...

Altium Designer学习笔记2
原理图的绘制 需要掌握的是系统自带原理图库元件的添加。...
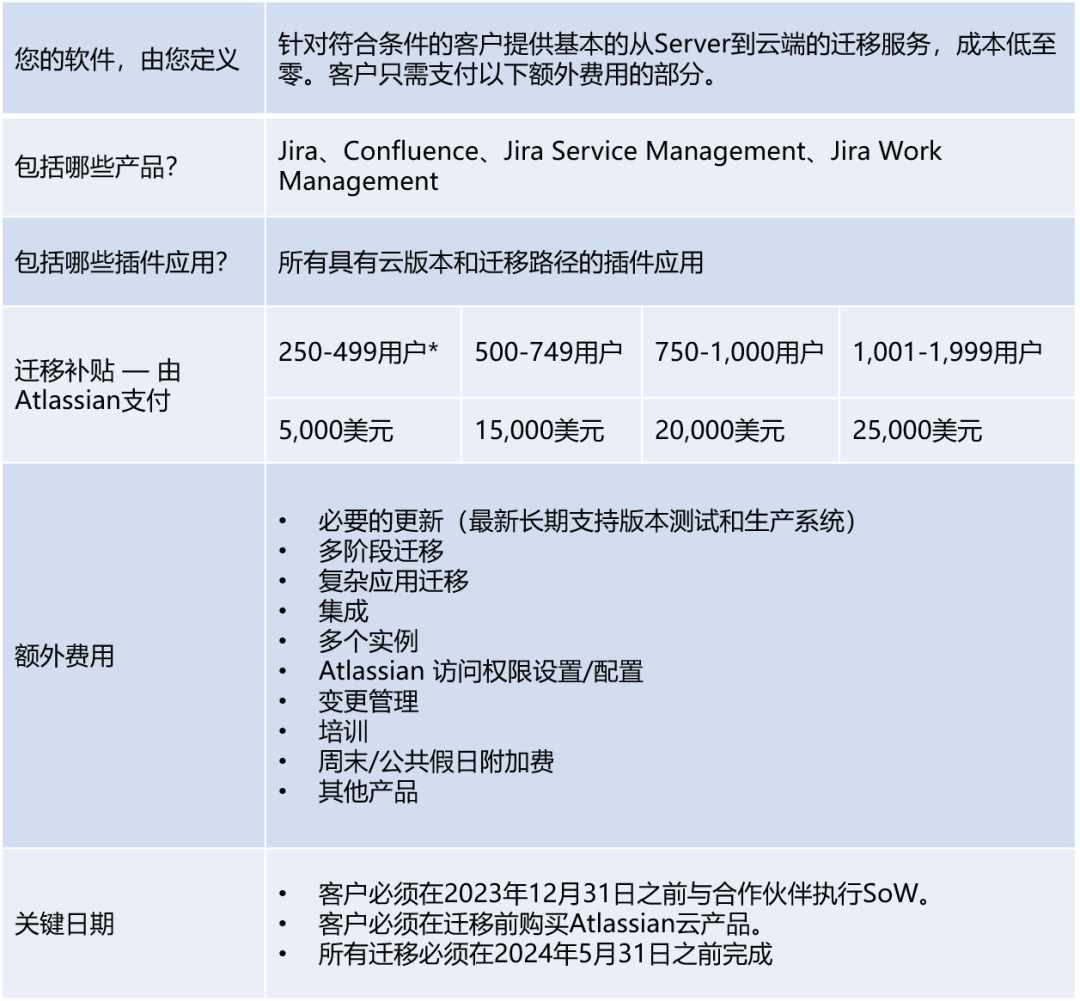
Atlassian发布最新补贴政策,Jira/Confluence迁移上云最低可至零成本
到2024年2月15日,Atlassian将不再提供对Jira、Confluence、Jira Service Management等Server版产品的支持。 近期,Atlassian推出了一项针对云产品的特殊优惠。现在从Server版迁移到云版,您能享受到高额补贴,甚至成本低至零元。立…...

基于FPGA的五子棋(论文+源码)
1.系统设计 在本次设计中,整个系统硬件框图如下图所示,以ALTERA的FPGA作为硬件载体,VGA接口,PS/2鼠标来完成设计,整个系统可以完成人人对战,人机对战的功能。系统通过软件编程来实现上述功能。将在硬件设计…...
QT5 MSVC2017 64bit配置OpenCV4.5无需编译与示范程序
环境:Windows 10 64位 Opencv版本:4.5 QT:5.14 QT5 MSVC2017配置OpenCV 版本参考: opencv msvc c对应版本 1.安装MSVC2017(vs2017) 打开Visual Studio Installer,点击修改 选择vs2017生成工…...
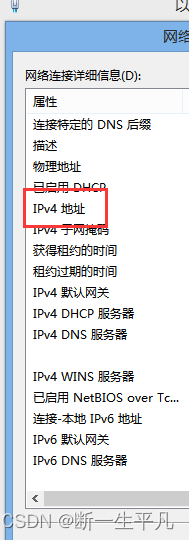
windows如何查看自己的ip地址
windows如何查看自己的ip地址 1.打开控制面板 2.进入网络和internet 3.进入网络共享中心 4.点击以太网进入网络详情页,或邮件已连接的网络,点击属性 5.查看ipv4地址就是当前机器ip...

Camera2的使用【详细】
目录 1.获取权限 2. 获取指定相机ID (1)获取相机管理者CameraManager (2)获取相机ID列表 (3)获取相机特征CameraCharacteristics (4)获取相机朝向 3.获取相机输出尺寸 (1)根据相机ID获取相机特征 (2)获取输出流配置StreamConfigurationMap (3)获取输出尺寸数组(参数为…...
Playcanvas后处理-辉光bloom
(一)Bloom介绍 Bloom(辉光、光晕、泛光)是一种常见的摄像机后处理(PostProcessing)效果,用于再现真实世界相机的成像伪影。这种效果会产生从图像中明亮区域边界延伸的光条纹(或羽毛…...
GCC 学习
GCC Resource Center for GCC Internalshttps://www.cse.iitb.ac.in/grc/这是个不错资料网站,有兴趣的可以了解下...
2023数维杯数学建模C题完整版本
已经完成全部版本,获取请查看文末下方名片 摘要 随着人工智能在多个领域的快速发展,其在文本生成上的应用引起了广泛关注。本研究聚焦于辨识人工智能(AI)生成文本的基本规则,并探究AI文本的检测及其与人类文本的区分…...

快速解密PPT幻灯片密码,让PPT重见天日
最简单的办法解密、找回和去除PPT幻灯片密码,具体步骤如下:1.百度搜索【密码帝官网】,2.点击“立即开始”在用户中心上传要解密的文件稍等片刻,就能找回密码。不用下载软件,手机电脑都可用。而且还支持Word、Excel、PD…...

十六、RabbitMQ快速入门
目录 一、在centos上下载MQ镜像 二、安装运行容器 三、登录进入MQ 1、添加一个新的用户 2、新建虚拟机 3、 为用户分配权限 四、RabbitMQ的基本概念 RabbitMQ中的几个概念: 五、常见消息模型 六、简单的消息生产与消费 1、消费者类 2、生产者类 3、基本消息队列的消…...
C#WPF用户控件及自定义控件实例
本文演示C#WPF自定义控件实例 用户控件(UserControl)和自定义控件(CustomControl)都是对UI控件的一种封装方式,目的都是实现封装后控件的重用。 只不过各自封装的实现方式和使用的场景上存在差异。 1 基于UserControl 创建 创建控件最简单一个方法就是基于UserControl …...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
