【机器学习基础】K-Means聚类算法
🚀个人主页:为梦而生~ 关注我一起学习吧!
💡专栏:机器学习 欢迎订阅!相对完整的机器学习基础教学!
⭐特别提醒:针对机器学习,特别开始专栏:机器学习python实战 欢迎订阅!本专栏针对机器学习基础专栏的理论知识,利用python代码进行实际展示,真正做到从基础到实战!
💡往期推荐:
【机器学习基础】机器学习入门(1)
【机器学习基础】机器学习入门(2)
【机器学习基础】机器学习的基本术语
【机器学习基础】机器学习的模型评估(评估方法及性能度量原理及主要公式)
【机器学习基础】一元线性回归(适合初学者的保姆级文章)
【机器学习基础】多元线性回归(适合初学者的保姆级文章)
【机器学习基础】对数几率回归(logistic回归)
【机器学习基础】正则化
【机器学习基础】决策树(Decision Tree)
💡本期内容:前面介绍的各种模型都是有监督的模型,对于无监督,最经典的就是聚类算法,本文就来介绍一下主要的聚类方法。
文章目录
- 1 聚类算法分析概述
- 2 K-Means聚类算法
- 3 K-Means参数概念及公式推导
- 3.1 平方误差(Sum of Squared Errors)
- 3.2 欧氏距离(euclidean metric)
- 3.3 轮廓系数(Silhouette Coefficient)
- 3.4 DB指数(Davies-Bouldin Index)
- 4 K-Means聚类算法的实现
- 4.1 算法流程
- 4.2 算法的伪代码描述
- 4.3 算法优缺点
1 聚类算法分析概述
近几年,随着网络的发展,越来越多的人开始习惯于在网上找信息,而网络也逐渐地走进了人们的日常生活。从人们每天都会接触到大量的数据,比如文字、音乐、图像、视频等等。随着信息的增多,人工智能应运而生。而在人工智能这个概念中,机器学习尤为重要,是实现人工智能的基础。机器学习,就是让计算机具有人一样的学习能力的技术,对当前和历史的海量数据进行挖掘、分析,并从中发现有价值的信息和规律。

随着大数据时代的来临,数据挖掘技术逐渐成为一种通用的业务方式,并推动了机器学习技术的快速发展。2021年,我国电商交易额为42.30万亿元,较上年同期增加了19.6%。在电商和其他行业中,要想获得更好的用户体验,就必须要对新用户进行类型的识别,这时,就可以将新用户进行聚类,将其分成多个簇,之后再以获得的结果为依据,来训练分类模型,进而判别新用户的类型。但是传统的数据挖掘技术已经不能适应海量的数据,K-Means聚类算法依赖其较简单的推导过程和实用、简单和高效的特性等广受青睐,在很多领域有巨大的贡献,例如:文档聚类、市场细分、图像分割、特征学习等。在非监督学习领域,K均值聚类是最广泛的,也是研究最多,应用最广泛的。而在聚类算法中,最常见的就是原型聚类(也称原型判别),以K均值算法为代表。
2 K-Means聚类算法
给定或随机产生m个样本的样本集。为了描述每个示例(即样本),我们给出了这样一个假设:每个示例具有d个属性来描述,这些属性反映了它与其他示例的关系,即每个示例是d维样本空间中的一个向量。
K-Means算法的基本思想是:将数据集按照距离进行划分,对于每一个样本,将它的邻域内的所有样本都分配到最近的那个类中。
首先,算法需要预先指定并且划分为k个簇,这也是与其他算法的不同点。在这里定义簇的均值向量为:

基于此,定义簇内样本围绕簇均值向量的紧密程度[13],即平方误差为:

E的值越小则簇内样本相似度越高,K-Means算法就是通过通过最小化SSE来寻找使得模型预测误差最小的模型参数。
3 K-Means参数概念及公式推导
3.1 平方误差(Sum of Squared Errors)
在聚类分析中,平方误差(Sum of Squared
Errors,SSE)是一种衡量聚类效果的指标。聚类算法将数据点分配到不同的簇中,每个数据点与它所属的簇的质心之间的距离被计算出来,然后平方,最后这些平方距离的和被称为平方误差。
具体来说,对于每个数据点xi和它所属的簇ci的质心,平方误差会计算为(xi - ci)^2。然后,所有簇的平方误差会相加,得到总的平方误差。这个值越小,说明每个数据点与它所属的簇的质心之间的距离越小,也就是聚类效果越好。

这个概念可以用于评估和优化聚类算法。比如在K-means算法中,初始质心的选择可能会影响聚类结果。K-means++ 算法通过让选择的质心尽可能分散来改善这个问题。另外,二分K-means算法则通过反复将一个簇划分为两个簇,直到达到用户给定的簇数目为止。在这个过程中,被划分出去的总是误差平方和最大的簇,因为这通常意味着这个簇的聚类效果最不好。
3.2 欧氏距离(euclidean metric)
也被称为欧几里得度量,是一个经常使用的在m维空间中两点之间的距离定义,或者向量的自然长度,即该点到原点的距离。在二维和三维空间中的欧氏距离就是两点之间的实际距离。
在聚类分析中,欧氏距离是常用的距离度量方式之一。它表示的是在n维空间中,两个点之间的直线距离。
具体计算公式为:

其中,x和y是两个n维向量,x1,x2,…,xn和y1,y2,…,yn是它们的对应维度上的值。
在应用方面,欧氏距离经常被用于衡量数据点之间的相似度,数据点之间的距离越小,说明它们越相似。例如,在客户分群中,可以使用该算法将相似行为模式的客户归类到同一簇中,以便进行个性化推荐和精准营销。在图像分析中,可以使用该算法将相似的图像归类到同一簇中,以便进行图像检索和内容识别。
- 缺点
例如,它对数据的尺度敏感,需要对数据进行归一化处理,以避免尺度差异对聚类结果的影响。此外,它只考虑了数据点之间的距离,没有考虑到数据点之间的方向关系,因此在处理某些特殊数据集时可能会出现聚类效果不佳的情况。
3.3 轮廓系数(Silhouette Coefficient)
轮廓系数(Silhouette Coefficient)是一种用于评估聚类效果的指标,它考虑了聚类中的内聚度和分离度。
轮廓系数的计算涉及到每个数据点和其所属簇内其他数据点的距离,以及该数据点与其他簇的距离。具体而言,对于每个数据点,其轮廓系数被定义为:s = (b - a) / max(a, b),其中a是数据点与其同簇其他数据点的平均距离,b是数据点与其他簇的平均距离。
轮廓系数计算公式如下:

根据轮廓系数的定义,si接近1时,说明样本i聚类合理;si接近-1时,说明样本i更应该分类到另外的簇;若si近似为0,则说明样本i在两个簇的边界上。所有样本的si的均值称为聚类结果的轮廓系数,是该聚类是否合理、有效的度量。

- 优点
它可以用于处理不等簇大小的情况,因为它考虑了每个样本点与其他簇的平均距离。
轮廓系数的值域为[-1,1],方便理解和使用。
- 局限性
它对异常值比较敏感,可能会受到离群点的影响。
3.4 DB指数(Davies-Bouldin Index)
DB指数(Davies-Bouldin Index)是一种用于评估聚类效果的内部指标。它考虑了每个簇内的样本点的紧密程度以及不同簇之间的分离度。
DB指数的计算方法如下:
- 对于每个簇Ck,计算其内部样本点之间的平均距离avg(Ck)。
- 对于每个簇Ck,计算其与其它簇之间的最小样本距离dmin(Ck, Cj)。
- 对于每个簇Ck,计算其中心点与其它簇中心点之间的距离dcen(Ck, Cj)。
- 计算DB指数,公式为:DBI=k1i=1∑kmaxj̸=i(dcen(ui,uj)avg(Ci)+avg(Cj))。
DB指数的值越小,说明聚类效果越好。这是因为DB指数衡量的是不同簇之间的分离度和簇内的紧密程度之间的平衡,当DB指数越小,说明聚类效果越好。
- 缺点
DB指数对于异常值比较敏感,因为异常值可能会影响簇内样本点的平均距离的计算。
此外,DB指数也可能会受到样本规模的影响,因为样本规模的增加可能会增加计算量,从而影响聚类效果的评价。
DB指数在计算过程中需要知道真实标签信息,因此常常被用作无监督聚类算法的评价指标,在比较不同算法或不同参数设置时提供了重要的帮助。
4 K-Means聚类算法的实现
K-Means聚类算法的基本原理是,针对聚类簇划分,最小化平方误差。平方误差在一定程度上描述了簇内样本点围绕簇均值向量的紧密程度,它的值越小说明聚类效果越好。
4.1 算法流程
- 从数据中选择K个对象作为初始聚类中心。
- 计算每个聚类对象到聚类中心的距离,将每个对象归到距离最近的聚类中心所对应的类别。
- 对于每个聚类,计算其所有数据点的均值,作为新的聚类中心。
- 如果聚类中心发生变化,返回第2步;否则算法结束。
- 整个算法会反复迭代第2步至第4步,直到聚类中心不再发生变化或达到最大迭代次数为止。最终,算法将会得到聚类结果,将每个数据点划分到不同的聚类中心所对应的类别中。

4.2 算法的伪代码描述

K-Means聚类算法的执行效果如下图所示:

4.3 算法优缺点
-
优点
首先,此算法容易理解、方便实现,其次,K均值算法可以看作高斯混合聚类在混合成分方差相等、且每个样本仅派给一个混合成分时的特例,所以该算法在数据集近似高斯分布时,聚类效果不错。同时,该算法可以处理大规模数据集,效率高。 -
缺点
但是,缺点也很显然。K值和初始聚类点的选取对于聚类的效果可能产生较大的影响,其次,样本点的离散程度可能对于聚类影响有较大的差别,特别是离群点的处理问题。由于K-Means聚类算法只能使用欧氏距离进行计算,所以只能较好的适用于椭球形类簇,对于非凸形状的簇不适合。K-Means算法只能处理数值型数据,对于非数值型数据需要进行转换才能使用。最后,由于此算法的时间复杂度为 O ( n k t ) O(nkt) O(nkt),所以在大规模数据上收敛较慢甚至引起崩溃。
相关文章:

【机器学习基础】K-Means聚类算法
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习 欢迎订阅!相对完整的机器学习基础教学! ⭐特别提醒:针对机器学习,特别开始专栏:机器学习python实战…...
Vite - 配置 - 自动修改 index.html 中的title
需求描述 在Vue3项目的开发过程中,我们为了能区分正式环境和测试环境, 通常会进行环境配置文件的区分, 例如,开发环境一个配置文件、生产环境一个配置文件。因此,我们就希望 在项目的index.html 的 title 标签中&…...
基于安卓android微信小程序美容理发店预约系统app
项目介绍 为美容院设计一个系统以减少员工的工作量就成为了想法的初始状态。紧接着对美容院进行进一步的调查发现我的想法已然落后。基本上每个美容院都以有了自己的信息系统,并且做的已经较完善了。 在这时我突然想到,现在关注美容养生的人越来越多&am…...

*** stack smashing detected ***: terminated
有一个函数返回值是bool类型,但忘了return了,编译可以通过,但是运行的时候报这个错误。...
鸿蒙系统扫盲(二):再谈鸿蒙是不是安卓套壳?
最近小米发布了澎湃OS,vivo发布了蓝OS,好像自从华为回归后,大伙都开始写自己的OS了,小米官方承认是套壳安卓,然后被大家喷了,于是鸿蒙是不是安卓套壳的话题又回到了大众的视野,今天在讨论下这个…...
PG数据中DBeaver上传csv文件作为数据表
DBeaver 是一个开源的数据库工具,还是蛮好用的,有时候需要我们上传数据做表,数据为CSV格式的,DBeaver本身自带有功能实现的。 可打开连着的数据库,找到模式,点到下面的表里,选择一个表直接导入…...

第十七篇-Awesome ChatGPT Prompts-备份-百度翻译
Awesome ChatGPT Prompts——一个致力于提供挖掘ChatGPT能力的Prompt收集网站 https://prompts.chat/ 第十六篇-Awesome ChatGPT Prompts-备份【英文】 第十七篇-Awesome ChatGPT Prompts-备份-百度翻译 【中文】 高效提示词请参考,各种场景,2023-11-16内容如下(百…...
[Android] Amazon 的 android 音视频开发文档
https://developer.amazon.com/zh/docs/fire-tv/audio-video-synchronization.html#22-getplaybackheadposition-api-level-3https://developer.amazon.com/zh/docs/fire-tv/audio-video-synchronization.html#22-getplaybackheadposition-api-level-3...

UE4基础篇十六:自定义 EQS 生成器
UE4 中的 EQS 带有一组很好的查询项生成器,但在某些情况下,您可能更喜欢根据需要创建生成器。我决定编写自己的生成器,因为我必须编写一个查询来找到查询器周围的最佳位置,但又不能太靠近它。我知道我可以添加一个距离测试来随着距离增加分数,但我什至不想考虑距查询器一定…...
轿车5+1汽车变速器变速箱同步器操纵机构机械结构设计CAD汽车工程
wx供重浩:创享日记 对话框发送:汽车变速器 获取完整论文报告说明书工程源文件 变速器工程图 操纵机构3D图 一、机械式变速器的概述及其方案的确定 1.1 变速器的功用和要求 变速器的功用是根据汽车在不同的行驶条件下提出的要求,改变发动机…...

STM32F4移植SPI注意事项
一、注意事项 可以看我之前移植的文章,那些就不提了,记得要复用,把IO复用成对应的功能io,然后还要注意时钟,看你需要的功能,去调对应的时钟,把时钟调匹配了,基本上不会有问题。 比如…...
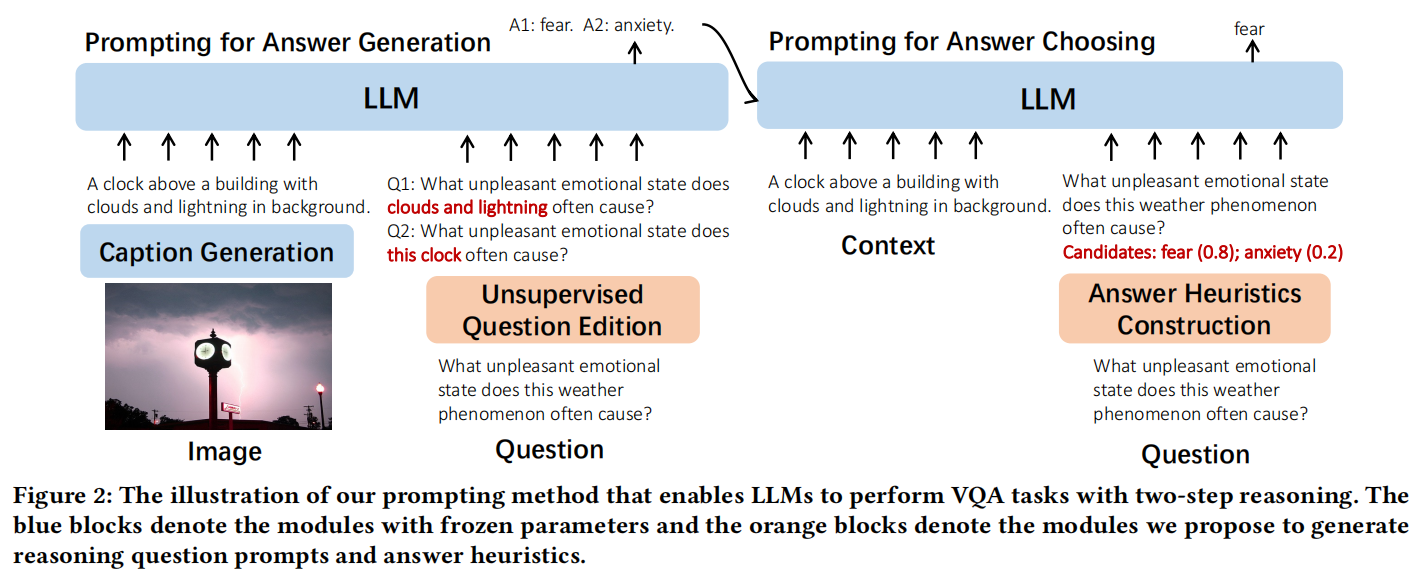
CV计算机视觉每日开源代码Paper with code速览-2023.11.16
点击CV计算机视觉,关注更多CV干货 论文已打包,点击进入—>下载界面 点击加入—>CV计算机视觉交流群 1.【基础网络架构】ConvNet vs Transformer, Supervised vs CLIP: Beyond ImageNet Accuracy 论文地址:https://arxiv.org//pdf/23…...
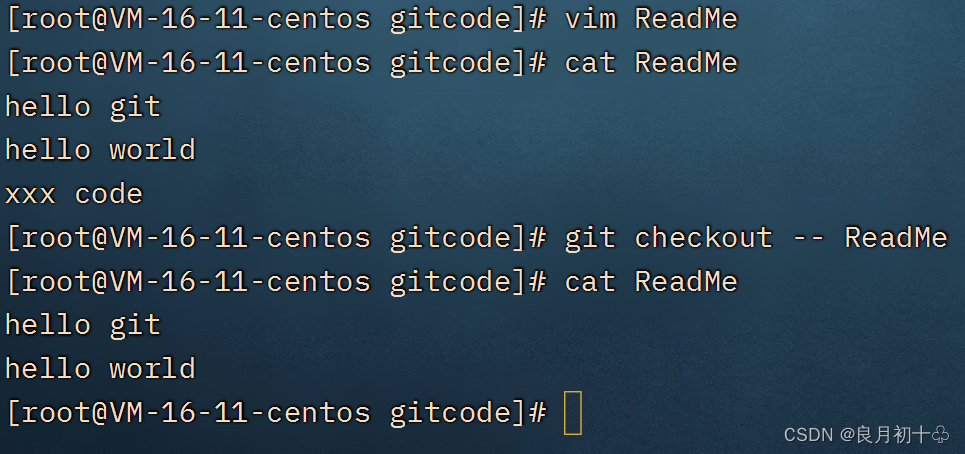
Git 简介及使用(1)
目录 一、在 Linux 环境中安装 Git 1. 先检查当前服务器中是否有 Git(如果有显示如下图) 2. 安装Git 3. 然后重复第一步:查看 Git 的版本信息即可 二、Git 的初始化及配置 1. 创建目录 2. 对仓库进行初始化 3. 新增两个配置项(…...
HTTPS流量抓包分析中出现无法加载key
HTTPS流量抓包分析(TLSv1.2),这篇文章分析的比较透彻,就不班门弄斧了 https://zhuanlan.zhihu.com/p/635420027 写个小问题:RSA密钥对话框加载rsa key文件的时候注意不要在中文目录下,否则会提示:“Enter the passwor…...

学习Rust适合写什么练手项目?【云驻共创】
Rust是一门备受关注的系统级编程语言,因其出色的内存安全性、高性能和并发性能而备受赞誉。对于那些希望学习和掌握Rust编程语言的人来说,练手项目是一个不可或缺的环节。通过实际动手完成项目,你可以加深对Rust语言特性和最佳实践的理解&…...
Spring Cloud学习(九)【Elasticsearch 分布式搜索引擎01】
文章目录 初识 elasticsearch了解 ES倒排索引ES 的一些概念安装es、kibana安装elasticsearch部署kibana 分词器安装IK分词器ik分词器-拓展词库 索引库操作mapping 映射属性索引库的 CRUD 文档操作添加文档查看、删除文档修改文档Dynamic Mapping RestClient 操作索引库什么是Re…...
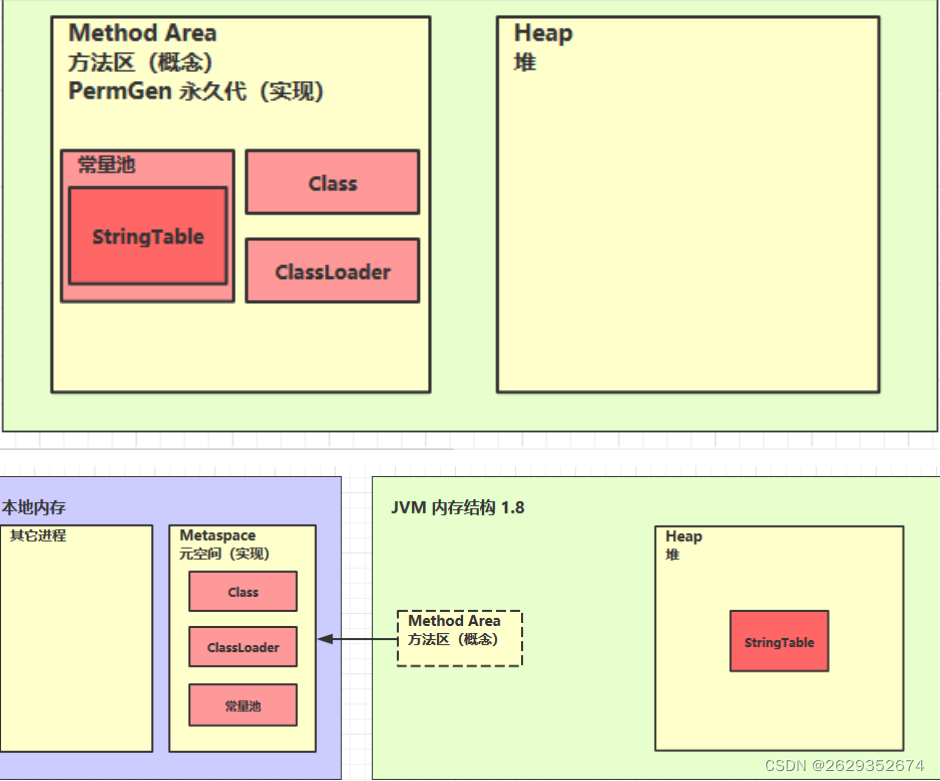
jvm 内存结构 ^_^
1. 程序计数器 2. 虚拟机栈 3. 本地方法栈 4. 堆 5. 方法区 程序计数器 定义: Program Counter Register 程序计数器(寄存器) 作用,是记住下一条jvm指令的执行地址 特点: 是线程私有的 不会存在内存溢出 虚拟机栈…...

SQL基础理论篇(八):视图
文章目录 简介创建视图修改视图删除视图总结参考文献 简介 视图,即VIEW,是SQL中的一个重要概念,它其实是一种虚拟表(非实体数据表,本身不存储数据)。 视图类似于编程中的函数,也可以理解成是一个访问数据的接口。 从…...
element-ui中怎样使用iconfont的图标
1 登录 https://www.iconfont.cn/ 2 搜索合适的图 这里可以找到这个图所在的图库。这样就可以一次查找到对应的所有同款图标 3 选择同款加入购物车 4 将购物车的icon加入项目,注意是新建项目,除非你是确定需要前面已经加过的icon 5 下载icon 选择fon…...

记一次struct2漏洞获取服务器
文章目录 一、漏洞原因二、漏洞成果三、漏洞利用0x01 struts2漏洞获取shell0x02 todesk配置文件获取连接0x03 orcal数据库连接0x04 web网站 sso管理权限0x05 tomcat网站0x06 获取路由器权限0x07 远程桌面四、总结五、免责声明一、漏洞原因 由于网站使用struct2框架,未及时进行…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...
