强化学习笔记
这里写自定义目录标题
- 参考资料
- 基础知识
- 16.3 有模型学习
- 16.3.1 策略评估
- 16.3.2 策略改进
- 16.3.3 策略迭代
- 16.3.3 值迭代
- 16.4 免模型学习
- 16.4.1 蒙特卡罗强化学习
- 16.4.2 时序差分学习
- Sarsa算法:同策略算法(on-policy):行为策略是目标策略
- Q-learning算法:异策略算法(off-policy):行为策略不是目标策略
- 多步时序差分:无偏且方差小
- 16.5 值函数近似
- 16.6 模仿学习
- 16.6.1 直接模仿学习
- 16.6.2 逆强化学习
- 深度Q网络算法
- 经验回放(experience replay)
- 目标网络(target network)
- deep Q network, DQN
- Double Deep Q-Network
- 优先级经验回放 (prioritized experience replay, PER)
- Dueling Deep Q-Network
- 策略梯度 Policy Gradients
- REINFORCE:蒙特卡洛策略梯度
- 近端策略优化(proximal policy optimization,PPO)
- Actor-Critic
- 信赖域策略优化 (Trust Region Policy Optimization, TRPO)
- 深度确定性策略梯度 (Deep Deterministic Policy Gradient, DDPG)
- Soft Actor-Critic
参考资料
《机器学习》周志华
《机器学习》(西瓜书)公式详解
南瓜书PumpkinBook
Reinforcement Learning: An Introduction
second edition
Richard S. Sutton and Andrew G. Barto
incompleteideas代码
张尚彤代码
周沫凡强化学习
周沫凡强化学习代码
周沫凡Python tutorial
张伟楠,沈键,俞勇
动手学强化学习
动手学强化学习代码
蘑菇书
王琦,杨毅远,江季,Easy RL:强化学习教程,人民邮电出版社,2022.
Easy RL:强化学习教程
面向非地面网络的智能无线资源管理机制与算法研究
[1]曹阳. 面向非地面网络的智能无线资源管理机制与算法研究[D]. 电子科技大学, 2023. DOI: 10.27005/d.cnki.gdzku.2023.000168.
波束成形论文代码
中文整理的强化学习资料
我的笔记2020年简书
我的笔记2020年CSDN
model-free
| 回合更新/单步更新 | on-policy / off-policy | 基于概率/基于价值 | 策略 | 状态 | 动作 | |
|---|---|---|---|---|---|---|
| Monte Carlo | 回合更新 | on-policy / off-policy | ||||
| Sarsa | 单步更新 | on-policy | 基于价值 | 离散 | 离散 | |
| Q learning | 单步更新 | off-policy | 基于价值 | 离散 | 离散 | |
| DQN | 单步更新 | off-policy | 基于价值 | 连续 | 离散 | |
| Policy Gradients | 基础版的policy gradients是回合更新。升级版的policy gradients是单步更新。 | on-policy | 基于概率 | 随机 | 连续 | |
| REINFORCE | 回合更新 | on-policy | 基于概率 | 随机 | 连续 | |
| Actor-Critic | on-policy | actor会基于概率做出动作。critic会对做出的动作给出动作的价值。 | ||||
| TRPO | on-policy | 随机 | ||||
| PPO | on-policy | 随机 | ||||
| DDPG | off-policy | 确定 | 连续 | |||
| Soft Actor-Critic | 随机 |
基础知识
以单智能体强化学习为例,具体的MDP数学模型M可以概括为M={S,A,R,P},其中,S,A,R和P分别表示智能体的状态集合、动作集合,奖励函数集合和状态转移概率集合。
强化学习任务对应了四元组 E= (X,A,P,R)
- 状态空间X
- 动作空间A
- 状态转移概率P:X×A×X→实数域
- 奖赏R:X×A×X→实数域
确定性策略:a=π(x),即在状态x下执行a动作;
随机性策略:P=π(x,a),即在状态x下执行a动作的概率。
强化学习在某种意义上可看作具有“延迟标记信息”的监督学习问题
K-摇臂赌博机
仅探索法:将尝试的机会平均分给每一个动作,即轮流执行,最终将每个动作的平均奖赏作为期望奖赏的近似值。
仅利用法:将尝试的机会分给当前平均奖赏值最大的动作。
欲累积奖赏最大,则必须在探索与利用之间达成较好的折中
ε-贪心法:基于一个概率来对探索和利用进行折中
以概率ε进行探索:πε(s) = 以均匀概率从A中选取动作
以概率1-ε进行利用:πε(s) = π(s) = a r g m a x a Q ( s , a ) argmax_{a} Q(s,a) argmaxaQ(s,a),即选择当前最优的动作。
Softmax算法:基于当前每个动作的平均奖赏值来对探索和利用进行折中
τ趋于0时, Softmax 将趋于“仅利用”
τ趋于无穷大时, Softmax 将趋于“仅探索”
16.3 有模型学习
有模型学习:状态空间、动作空间、转移概率以及奖赏函数都已经给出
预测(prediction)和控制(control)是马尔可夫决策过程里面的核心问题。
预测(评估一个给定的策略)的输入是马尔可夫决策过程 <S,A,P,R,γ> 和策略π,输出是价值函数Vπ。
控制(搜索最佳策略)的输入是马尔可夫决策过程 <S,A,P,R,γ>,输出是最佳价值函数(optimal value function)V∗和最佳策略(optimal policy)π∗。
16.3.1 策略评估
状态值函数(V):Vπ(x),即从状态x出发,使用π策略所带来的累积奖赏;
状态-动作值函数(Q):Qπ(x,a),即从状态x出发,执行动作a后再使用π策略所带来的累积奖赏。
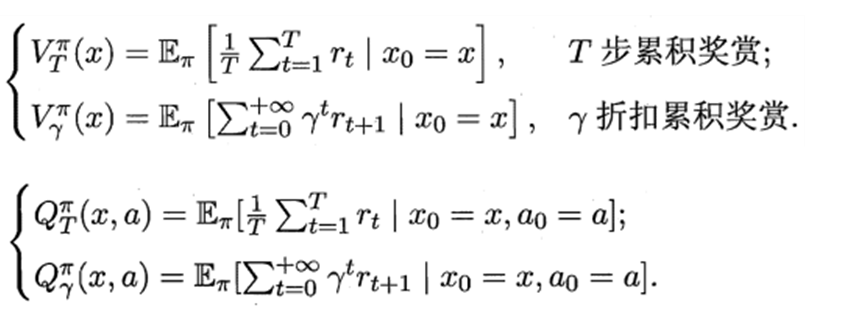
递归形式:Bellman 等式
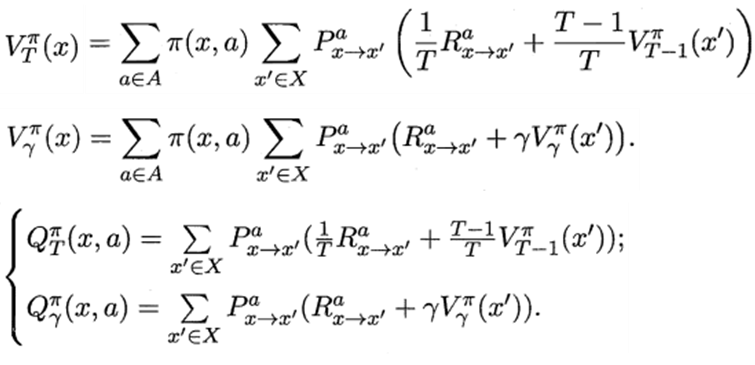
16.3.2 策略改进
最优策略:使得值函数对所有状态求和的值最大的策略
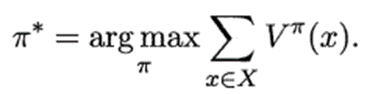
最优值函数:最优策略对应的值函数
策略改进:
16.3.3 策略迭代
策略迭代:不断迭代进行策略评估和策略改进,直到策略收敛、不再改变为止

16.3.3 值迭代
值迭代:不断迭代进行策略评估,直到值函数收敛、不再改变为止

16.4 免模型学习
在原始策略上使用ε-贪心策略
ε-贪心法:基于一个概率来对探索和利用进行折中
以概率ε进行探索:πε(s) = 以均匀概率从A中选取动作
以概率1-ε进行利用:πε(s) = π(s) = a r g m a x a Q ( s , a ) argmax_{a} Q(s,a) argmaxaQ(s,a),即选择当前最优的动作。
16.4.1 蒙特卡罗强化学习
蒙特卡罗强化学习:通过采样来进行策略评估。
多次“采样”,然后求取平均累积奖赏来作为期望累积奖赏的近似
由于采样必须为有限次数,因此该方法更适合于使用 步累积奖赏的强化学习任务。
估计状态-动作值函数

同策略(on-policy)蒙特卡罗强化学习算法:被评估和被改进的都是同一个策略
异策略(off-policy)蒙特卡罗强化学习算法:仅在评估时使用ε-贪心策略,而在改进时使用原始策略
蒙特卡罗强化学习算法没有充分利用强化学习任务的 MDP 结构
the target policy: the policy being learned about
the behavior policy: the policy used to generate behavior
In this case we say that learning is from data “off” the target policy, and the overall process is termed off-policy learning.
目标策略:正在被学习的策略
行为策略:被用来产生行为的策略
同策略(on-policy):行为策略是目标策略
智能体直接采用正在优化的策略函数收集训练数据,即利用自身在特定时间内产生的连续决策轨迹更新当前的DNN参数。
异策略(off-policy):行为策略不是目标策略。
智能体在收集训练数据时采用与正在优化的策略函数不一致的策略。
16.4.2 时序差分学习
蒙特卡罗强化学习算法在一个完整的采样轨迹完成后再对所有的状态-动作对进行更新。
实际上这个更新过程能增量式进行。
时序差分(Temporal Difference ,简称 TD )学习则结合了动态规划与蒙特卡罗方法的思想,能做到更高效的免模型学习。
Sarsa算法:同策略算法(on-policy):行为策略是目标策略
每次更新值函数需知道前一步的状态(state)x、前一步的动作(action)a、奖赏值(reward)R、当前状态(state)x’、将要执行的动作(action)a’:
Q ( s , a ) ← Q ( s , a ) + α [ R + γ Q ( s ′ , a ′ ) − Q ( s , a ) ] , γ ∈ [ 0 , 1 ) Q(s,a)←Q(s,a)+\alpha[R+\gamma Q\left(s^{\prime}, a^{\prime}\right)-Q(s,a)],\gamma∈[0,1) Q(s,a)←Q(s,a)+α[R+γQ(s′,a′)−Q(s,a)],γ∈[0,1)
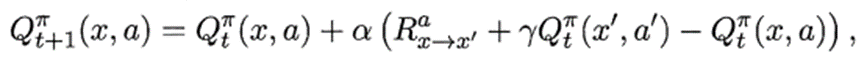
更新步长α越大,则越靠后的累积奖赏越重要。
π(s) = a r g m a x a Q ( s , a ) argmax_{a} Q(s,a) argmaxaQ(s,a)

on policy 同策略
在选择动作执行的时候采取的策略 = 在更新Q表的时候采取的策略
行为策略 行动策略是ε-greedy策略
目标策略 评估策略是ε-greedy策略
Q-learning算法:异策略算法(off-policy):行为策略不是目标策略
每次更新值函数需知道前一步的状态(state)x、前一步的动作(action)a、奖赏值(reward)R、当前状态(state)x’
Q值表:state为行,action为列,reward为元素
Q ( s , a ) ← Q ( s , a ) + α [ R + γ max a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ] , γ ∈ [ 0 , 1 ) Q(s,a)←Q(s,a)+\alpha[R+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime}\right)-Q(s,a)],\gamma∈[0,1) Q(s,a)←Q(s,a)+α[R+γmaxa′Q(s′,a′)−Q(s,a)],γ∈[0,1)
学习率*(Q的真实值 - Q的估计值)
如果学习率越大,那么新估计值代替旧估计值的程度也越大

off policy 异策略
在选择动作执行的时候采取的策略 ≠ 在更新Q表的时候采取的策略
行为策略 行动策略是ε-greedy策略
目标策略 更新Q表的策略是贪婪策略
Q-learning的目标策略不管行为策略会产生什么动作。Q-learning的目标策略默认下一个动作就是 Q 值最大的那个动作,并且默认按照最佳的策略去优化目标策略,所以它可以更大胆地去寻找最优的路径,它表现得比 Sarsa 大胆得多。
异策略算法的这个循环可以拆开成2个部分:与环境交互(执行动作,获得奖励和观察状态)和学习(用动作,奖励,状态更新Q),从而实现离线学习。
离线学习的行为策略一直没更新,训练效果应该也不好?
多步时序差分:无偏且方差小
蒙特卡洛方法利用当前状态之后每一步的奖励而不使用任何价值估计
时序差分算法只利用一步奖励和下一个状态的价值估计。
蒙特卡洛方法:无偏(unbiased),方差大
方差大,因为每一步的状态转移都有不确定性,而每一步状态采取的动作所得到的不一样的奖励最终都会加起来,这会极大影响最终的价值估计;
时序差分算法:有偏,方差小
方差小,因为只关注了一步状态转移,用到了一步的奖励
有偏,因为用到了下一个状态的价值估计而不是其真实的价值。
多步时序差分可以结合二者的优势
多步sarsa
Sarsa(0):Sarsa 是一种单步更新法, 在环境中每走一步, 更新一次自己的行为准则。等走完这一步以后直接更新行为准则
Sarsa(1):走完这步, 再走一步, 然后再更新
Sarsa(n):如果等待回合完毕我们一次性再更新呢, 比如这回合我们走了 n 步
Sarsa(lambda):有了一个 lambda 值来代替我们想要选择的步数
lambda 是脚步衰减值, 是一个在 0 和 1 之间的数
当 lambda 取0, 就变成了 Sarsa 的单步更新
当 lambda 取 1, 就变成了回合更新, 对所有步更新的力度都是一样
当 lambda 在 0 和 1 之间, 取值越大, 离宝藏越近的步更新力度越大
16.5 值函数近似
直接对连续状态空间的值函数进行学习
值函数能表达为状态的线性函数
线性值函数近似 Sarsa 算法
线性值函数近似 Q-learning算法
16.6 模仿学习
16.6.1 直接模仿学习
直接模仿人类专家的“状态-动作对"
16.6.2 逆强化学习
逆强化学习:从人类专家提供的范例数据中反推出奖赏函数
深度Q网络算法
Q-learning 算法:状态和动作都是离散的,并且空间都比较小的情况下适用
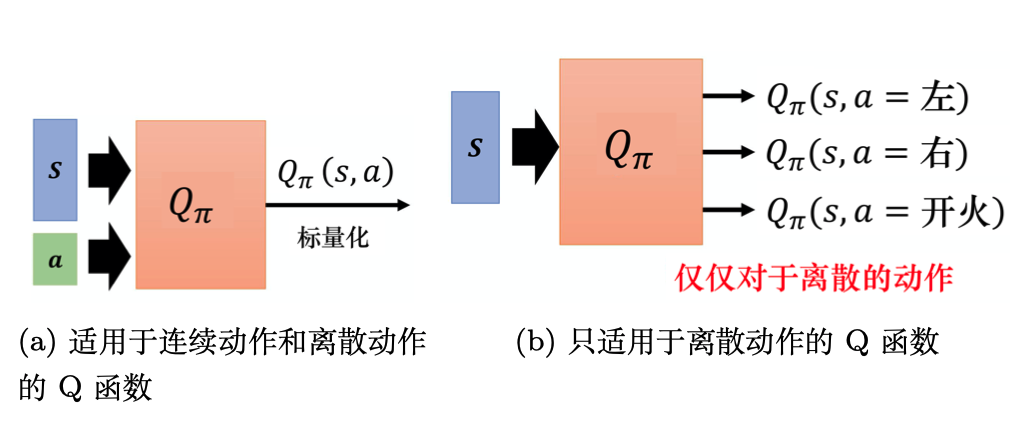
若动作是连续(无限)的,神经网络的输入:状态s和动作a。输出:在状态s下采取动作a能获得的价值。
若动作是离散(有限)的,除了可以采取动作连续情况下的做法,我们还可以:神经网络的输入:状态s。输出:每一个动作的Q值。
通常 DQN(以及 Q-learning)只能处理动作离散的情况,因为在Q函数的更新过程中有max_a这一操作。
Q网络:用于拟合Q函数的神经网络
DQN 算法最终更新的目标:最小化损失函数
Q 网络的损失函数构造为均方误差的形式:
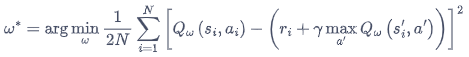
I = ( r + γ max a Q ( s ′ , a ′ , w ) − Q ( s , a , w ) ) 2 I=\left(r+\gamma \max _{a} Q\left(s^{\prime}, a^{\prime}, \mathbf{w}\right)-Q(s, a, \mathbf{w})\right)^{2} I=(r+γmaxaQ(s′,a′,w)−Q(s,a,w))2
经验回放(experience replay)
如果某个算法使用了经验回放,该算法就是异策略算法。
维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。
好处:
- 打破样本之间的相关性,让其满足独立假设。
在 MDP 中交互采样得到的数据本身不满足独立假设,因为这一时刻的状态和上一时刻的状态有关。
非独立同分布的数据对训练神经网络有很大的影响,会使神经网络拟合到最近训练的数据上。
回放缓冲区里面的经验来自于不同的策略,我们采样到的一个批量里面的数据会是比较多样的。 - 提高样本效率。
每一个样本可以被使用多次,十分适合深度神经网络的梯度学习。
与环境交互比较慢,训练网络比较快。
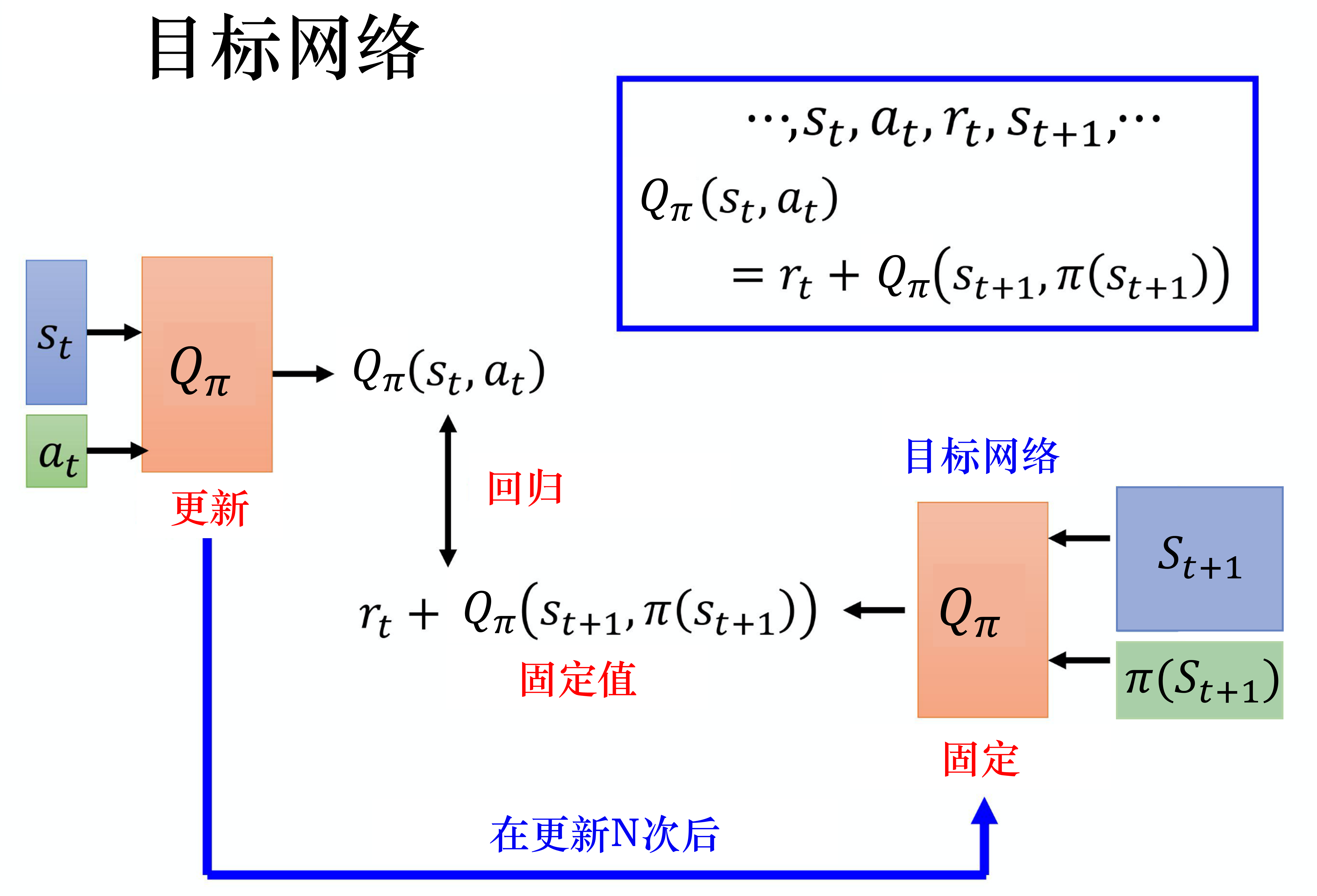
目标网络(target network)
损失函数包含神经网络的输出,因此在更新网络参数的同时目标也在不断地改变,这非常容易造成神经网络训练的不稳定性。
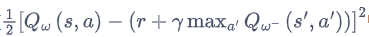
训练网络:用于计算损失函数的前一项,并且使用正常梯度下降方法来进行更新。
目标网络:用于计算损失函数的后一项
训练网络在训练中的每一步都会更新。
目标网络的参数每隔几步才会与训练网络同步一次。
这样做使得目标网络相对于训练网络更加稳定。
deep Q network, DQN

Double Deep Q-Network
[1509.06461] Deep Reinforcement Learning with Double Q-learning
DQN的问题:DQN算法通常会导致对Q值的过高估计
DQN:Q_next = max(Q_next(s’, a_all))
Y t D Q N ≡ R t + 1 + γ max a Q ( S t + 1 , a ; θ t − ) Y_{t}^{\mathrm{DQN}} \equiv R_{t+1}+\gamma \max _{a} Q\left(S_{t+1}, a ; \boldsymbol{\theta}_{t}^{-}\right) YtDQN≡Rt+1+γmaxaQ(St+1,a;θt−)
Double DQN:Q_next = Q_next(s’, argmax(Q_eval(s’, a_all)))
Y t DoubleDQN ≡ R t + 1 + γ Q ( S t + 1 , argmax a Q ( S t + 1 , a ; θ t ) ; θ t − ) Y_{t}^{\text {DoubleDQN }} \equiv R_{t+1}+\gamma Q\left(S_{t+1}, \underset{a}{\operatorname{argmax}} Q\left(S_{t+1}, a ; \boldsymbol{\theta}_{t}\right); \boldsymbol{\theta}_{t}^{-}\right) YtDoubleDQN ≡Rt+1+γQ(St+1,aargmaxQ(St+1,a;θt);θt−)
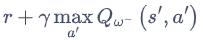
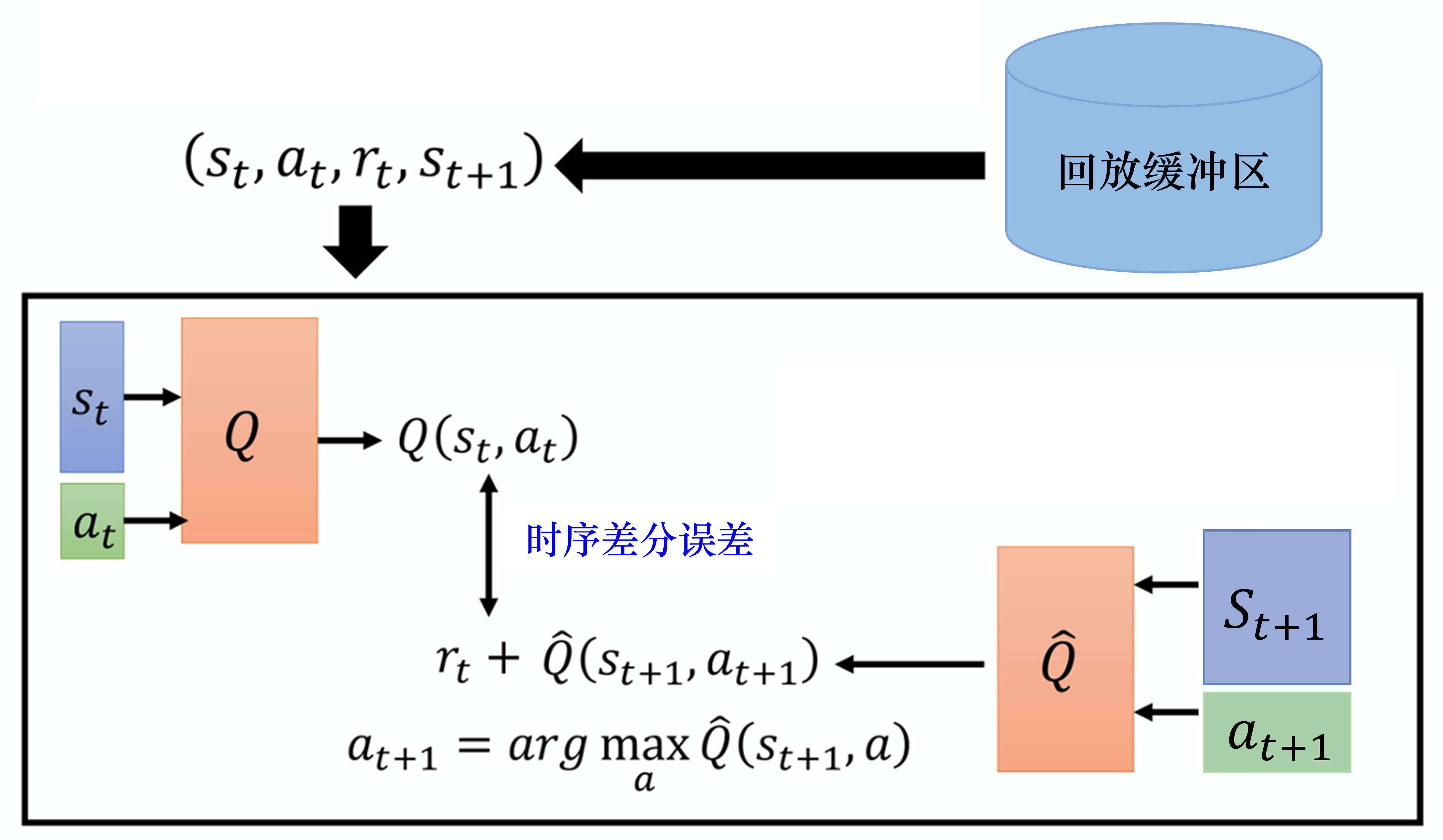
DQN的优化目标为 ,动作的选取依靠目标网络
,动作的选取依靠目标网络
Double DQN 的优化目标为 ,动作的选取依靠训练网络
,动作的选取依靠训练网络
用训练网络计算使Q值最大的动作
用目标网络计算Q值
当前的Q网络w用于选择动作
旧的Q网络w−用于评估动作
Double DQN 的代码实现可以直接在 DQN 的基础上进行,无须做过多修改。
优先级经验回放 (prioritized experience replay, PER)
[1511.05952] Prioritized Experience Replay
Double Learning and Prioritized Experience Replay
重视值得学习的样本
时序差分误差 = 网络的输出与目标之间的差距
如果采样过的数据的时序差分误差特别大,那么应该让它们以比较大的概率被采样到。

batch 抽样的时候并不是随机抽样, 而是按照 Memory 中的样本优先级来抽
用到 TD-error, 也就是 Q现实 - Q估计 来规定优先学习的程度
如果 TD-error 越大, 就代表我们的预测精度还有很多上升空间, 那么这个样本就越需要被学习, 也就是优先级 p 越高
Dueling Deep Q-Network
[1511.06581] Dueling Network Architectures for Deep Reinforcement Learning
Dueling DQN 能够很好地学习到不同动作的差异性,在动作空间较大的环境下非常有效。
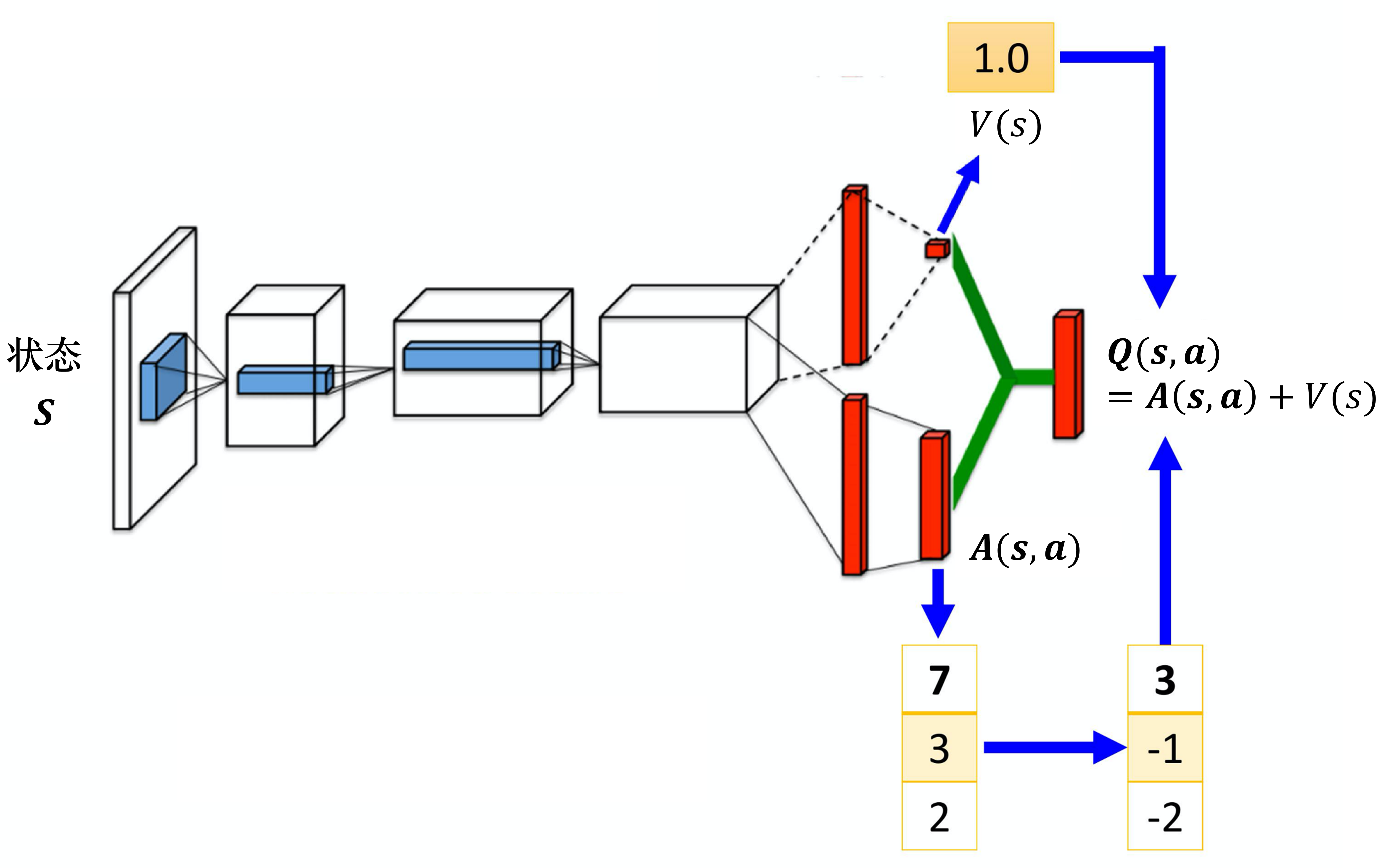
将Q网络分成两个通道
Q η , α , β ( s , a ) = V η , α ( s ) + A η , β ( s , a ) Q_{\eta, \alpha, \beta}(s,a) = V_{\eta, \alpha}(s) + A_{\eta, \beta}(s,a) Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a)
V η , α ( s ) V_{\eta, \alpha}(s) Vη,α(s):状态价值函数,与action无关
A η , β ( s , a ) A_{\eta, \beta}(s,a) Aη,β(s,a):该状态下采取不同动作的优势函数,与action有关
η \eta η是状态价值函数和优势函数共享的网络参数,一般用在神经网络中,用来提取特征的前几层
α \alpha α和 β \beta β分别为状态价值函数和优势函数的参数。
竞争深度Q网络的问题:最后学习的结果可能是这样的:
智能体就学到 V(s) 等于 0,A(s,a) 等于 Q,就和原来的深度Q网络一样。
解决方案:在把 A(s,a)与 V(s) 加起来之前,先处理A(s,a),比如减去均值
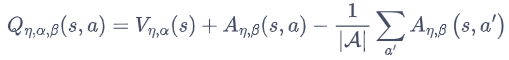
虽然它不再满足贝尔曼最优方程,但实际应用时更加稳定。
策略梯度 Policy Gradients
基于值函数的方法:学习值函数,然后根据值函数导出一个策略。学习过程中并不存在一个显式的策略
基于策略的方法:直接显式地学习一个目标策略。
REINFORCE:蒙特卡洛策略梯度
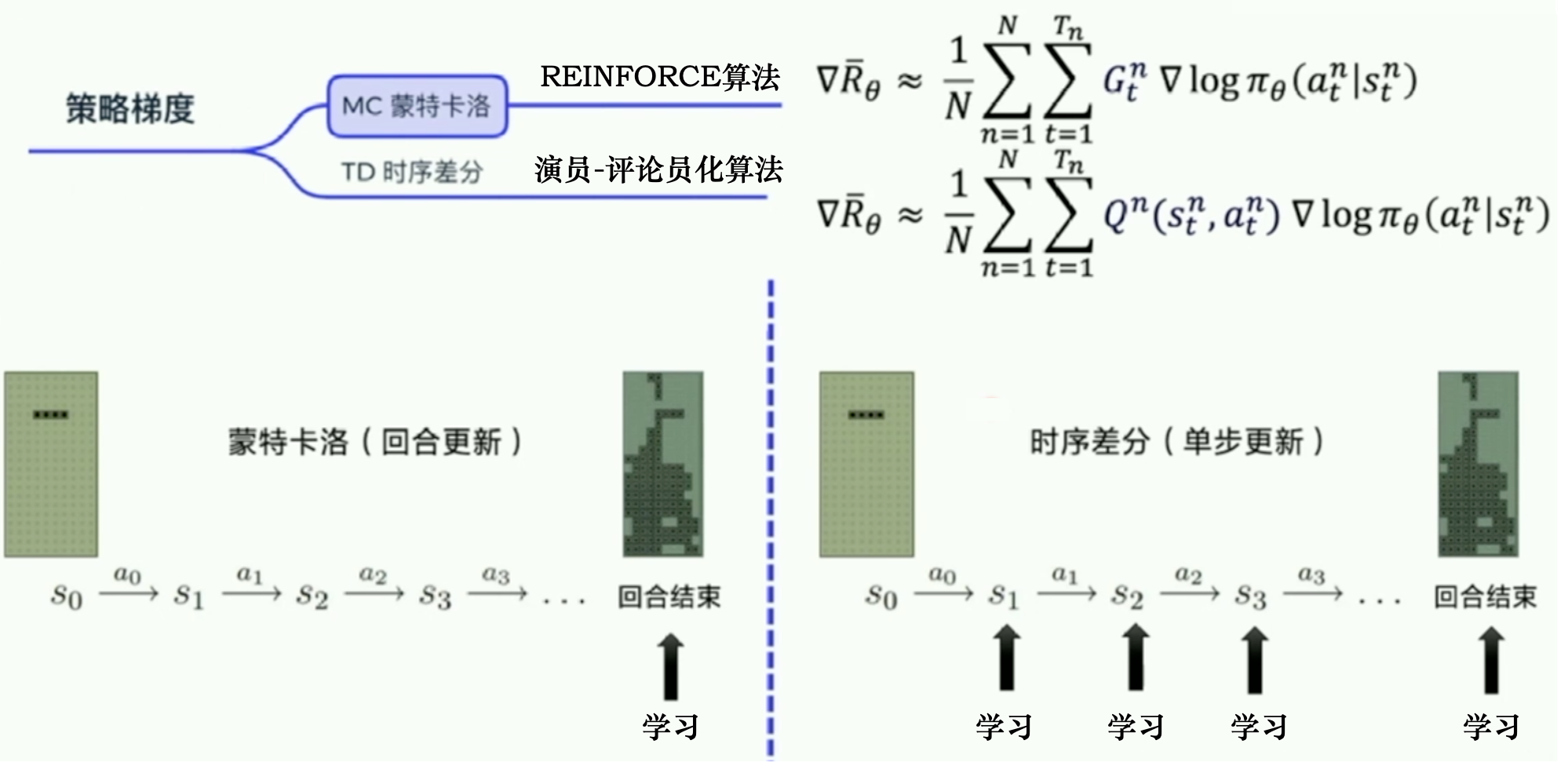
Gt:从第t步开始,往后能够获得的总奖励

因为使用了蒙特卡洛方法,REINFORCE 算法的梯度估计的方差很大
近端策略优化(proximal policy optimization,PPO)
Actor-Critic
信赖域策略优化 (Trust Region Policy Optimization, TRPO)
深度确定性策略梯度 (Deep Deterministic Policy Gradient, DDPG)
DDPG算法则采用行动者-批评家(actor-critic)模型,即采用两类分别称为行动者网络与批评家网络的不同DNN。
批评家网络即为传统的值函数,来评估不同状态下的收益;
行动者网络则指策略函数,描述状态和离散动作或连续动作分布的映射关系。
Soft Actor-Critic
相关文章:

强化学习笔记
这里写自定义目录标题 参考资料基础知识16.3 有模型学习16.3.1 策略评估16.3.2 策略改进16.3.3 策略迭代16.3.3 值迭代 16.4 免模型学习16.4.1 蒙特卡罗强化学习16.4.2 时序差分学习Sarsa算法:同策略算法(on-policy):行为策略是目…...

经典双指针算法试题(一)
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、移动零1、题目讲解2、讲解算法原理3、代码实现 二、复写零1、题目讲解2、讲解算法原理3、…...
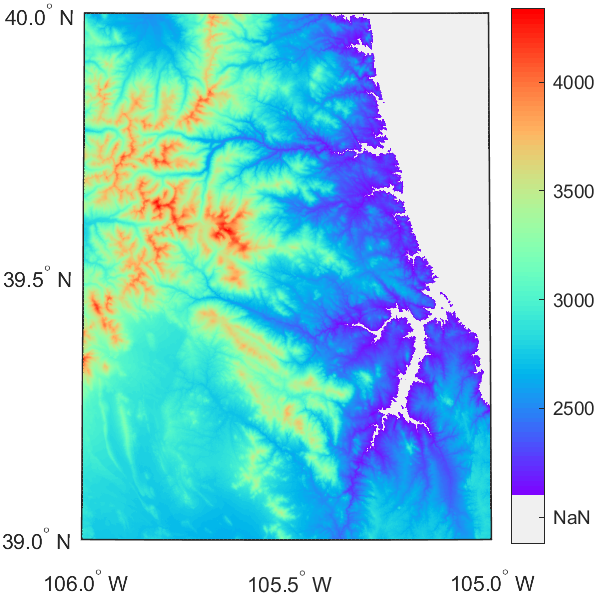
MATLAB | 绘图复刻(十三) | 带NaN图例的地图绘制
有粉丝问我地图绘制如何添加NaN,大概像这样: 或者这样: 直接上干货: 原始绘图 假设我们有这样的一张图地图,注意运行本文代码需要去matlab官网下载Mapping Toolbox工具箱,但是其实原理都是相似的&…...

netty整合websocket(完美教程)
websocket的介绍: WebSocket是一种在网络通信中的协议,它是独立于HTTP协议的。该协议基于TCP/IP协议,可以提供双向通讯并保有状态。这意味着客户端和服务器可以进行实时响应,并且这种响应是双向的。WebSocket协议端口通常是80&am…...

选择PC示波器的10种理由!
PC示波器(PCs)在测试仪器领域中的关键项目上正迅速地取代传统的数字存储示波器(DSOs),其中有十个理由: 小巧和便携示波器利用你的PC显示器实现大屏幕和精细彩色显示信号存储只受限于你的PC存储器大小捕捉波…...
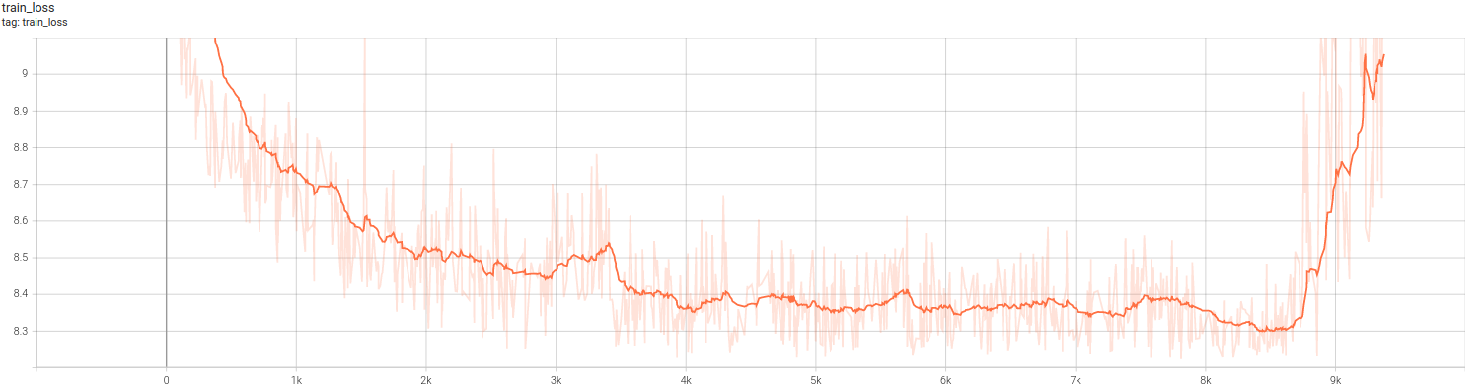
【pytorch深度学习 应用篇02】训练中loss图的解读,训练中的问题与经验汇总
文章目录 loss图解析train loss ↘ \searrow ↘ ↗ \nearrow ↗ 先降后升 loss图解析 train loss ↘ \searrow ↘ 不断下降,test loss ↗ \nearrow ↗ 不断上升:原因很多,我是把workers1,batchSize8192train loss ↘ \searro…...

uniapp 微信小程序如何实现多个item列表的分享
以下代码是某个循环里面的item <button class"cu-btn" style"background-color: transparent;padding: 0;"open-type"share" :data-tree"item.treeId" :data-project"item.projectId"v-if"typeId1 && userI…...
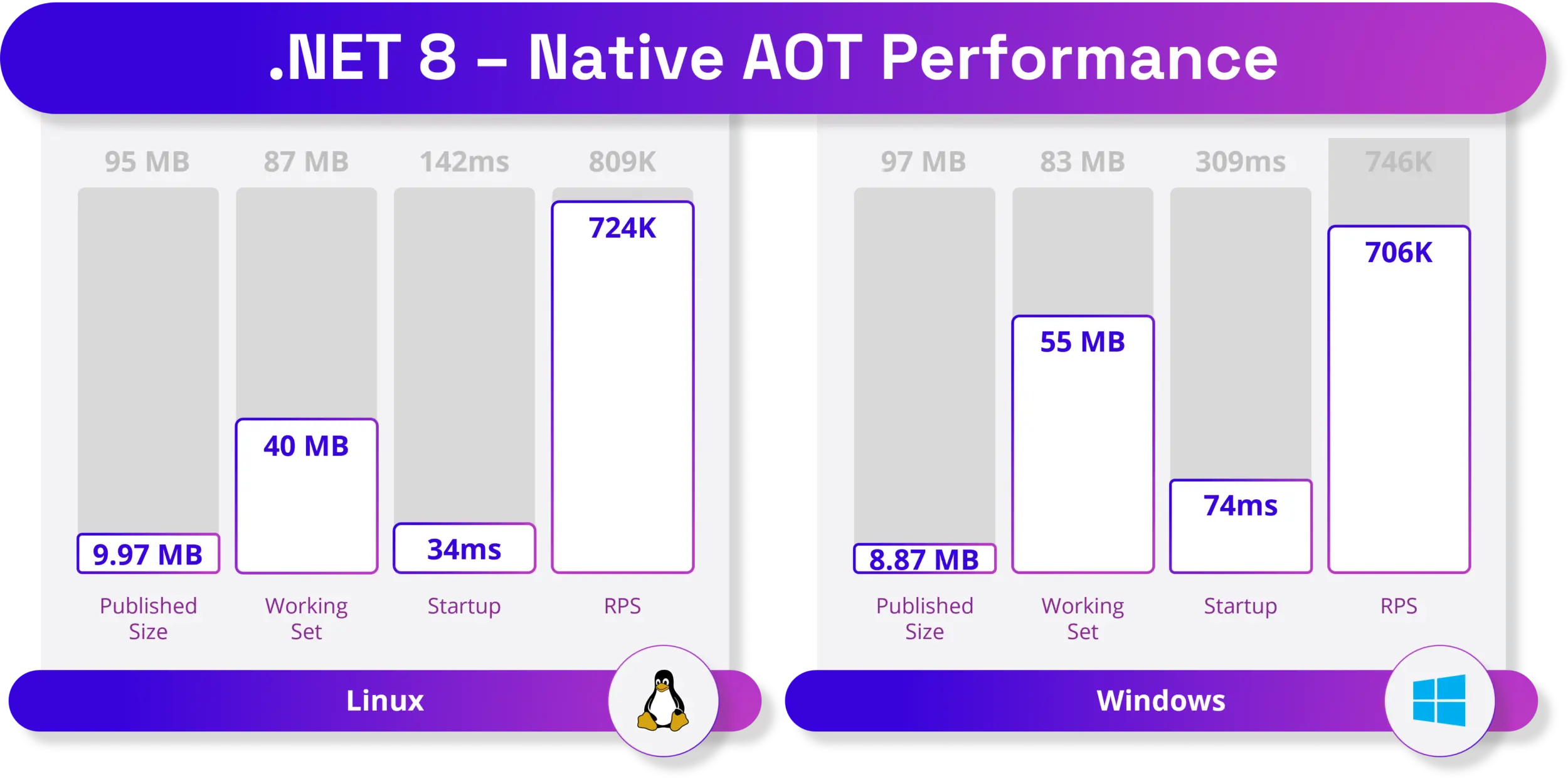
.NET 8 正式 GA 遥遥领先
.NET 8 一正式 已正式 GA。 微软称 .NET 8 提供了数以千计的性能、稳定性和安全性改进,以及平台和工具增强功能,有助于提高开发者的工作效率和创新速度。 比如 .NET 8 为 Android 和 WASM 引入了全新的 AOT 模式、改进 System.Text.Json,以…...

2216. 美化数组的最少删除数 --力扣 --JAVA
题目 给你一个下标从 0 开始的整数数组 nums ,如果满足下述条件,则认为数组 nums 是一个 美丽数组 : nums.length 为偶数对所有满足 i % 2 0 的下标 i ,nums[i] ! nums[i 1] 均成立 注意,空数组同样认为是美丽数组。…...

DDD 领域驱动设计
文章目录 请解释下什么是 DDD 领域驱动设计DDD 的四层领域模型是怎样的?包含哪些基础概念?DDD 中的贫血模型和充血模型有什么区别在 DDD 中,如何处理模型的聚合和聚合根DDD 中的实体和值对象有什么区别?在 DDD 中,如何…...
转型做视频了,博客就是稿子,继续坚持写博客,同时发布视频,能写博客说明思路清晰了,能再讲明白,理解就更透彻了,紧跟上时代发展。
1,今天特别记录下,B站给开通了《合集》功能 最近使用视频制作了几个视频。播放量还不错,最好的已经到了 2.6K了。 然后粉丝也涨到了 200个。 添加链接描述 紧跟时代:从写博客到录视频,粉丝大涨,突破200个&…...

小众市场:探索跨境电商中的利基领域
随着全球数字化和互联网的普及,跨境电子商务已经成为了一个蓬勃发展的产业。从亚马逊到阿里巴巴,大型电商平台已经占据了很大一部分市场份额。 然而,在这个竞争激烈的领域,寻找小众市场和利基领域可能是一种成功的策略。本文将探…...

C++中的mutable关键字
mutable是C中的一个关键字,它用来修饰类的成员变量。 当我们将一个成员变量声明为mutable时,就意味着这个成员变量可以被类的任何方法修改,即使这个方法是const类型的。这是因为mutable关键字可以打破const类型的限制,使得const类…...

java: 无效的目标发行版: 17 问题解决
今天在写完类点击运行后显示java: 无效的目标发行版: 17 网上查询了一番,发现有几个地方需要注意。 还有一个就是设置中,下面的就是我本次问题所在,不知道为什么,他自动添加了下面的东西 一个方法是把目标字节码版本改为正确的&a…...

C#的LINQ查询
当使用LINQ(Language Integrated Query)查询时,我们可以在C#中以一种类似于SQL的语法来查询数据。LINQ提供了一种统一的方式来查询各种数据源,如集合、数据库、XML等。 在上述示例中,我们使用LINQ查询来将两个列表根据…...

Python不会调试不够丝滑?那事你不会logging---剖析!
前言: 一直都是手动debug进行调试,F8都按烂了;最近用logging进行提前布置,发现这样更能让代码走得丝滑,同时也能尽早发现问题! 基本概念: Logger - 日志记录接口 Handler - 确定日志记录发送到不同的地方(文件、控制台等) Level - 定义了日…...
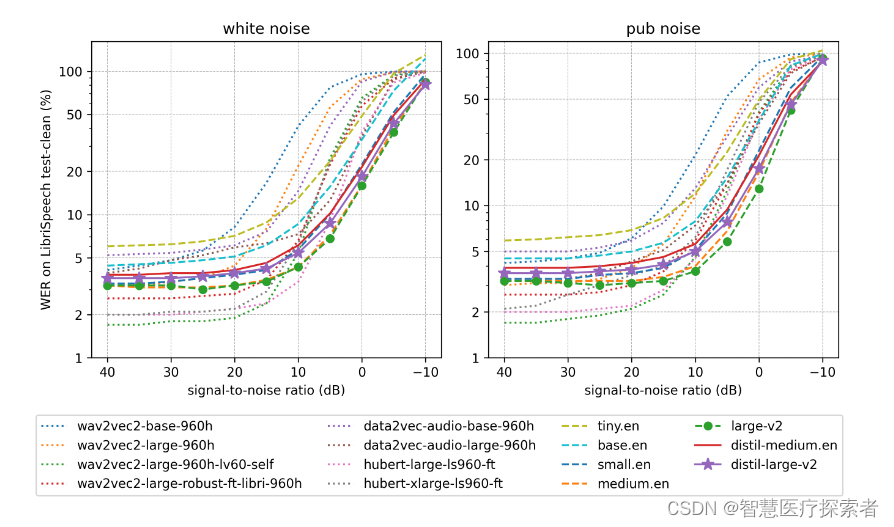
OpenAI的Whisper蒸馏:蒸馏后的Distil-Whisper速度提升6倍
1 Distil-Whisper诞生 Whisper 是 OpenAI 研发并开源的一个自动语音识别(ASR,Automatic Speech Recognition)模型,他们通过从网络上收集了 68 万小时的多语言(98 种语言)和多任务(multitask&am…...
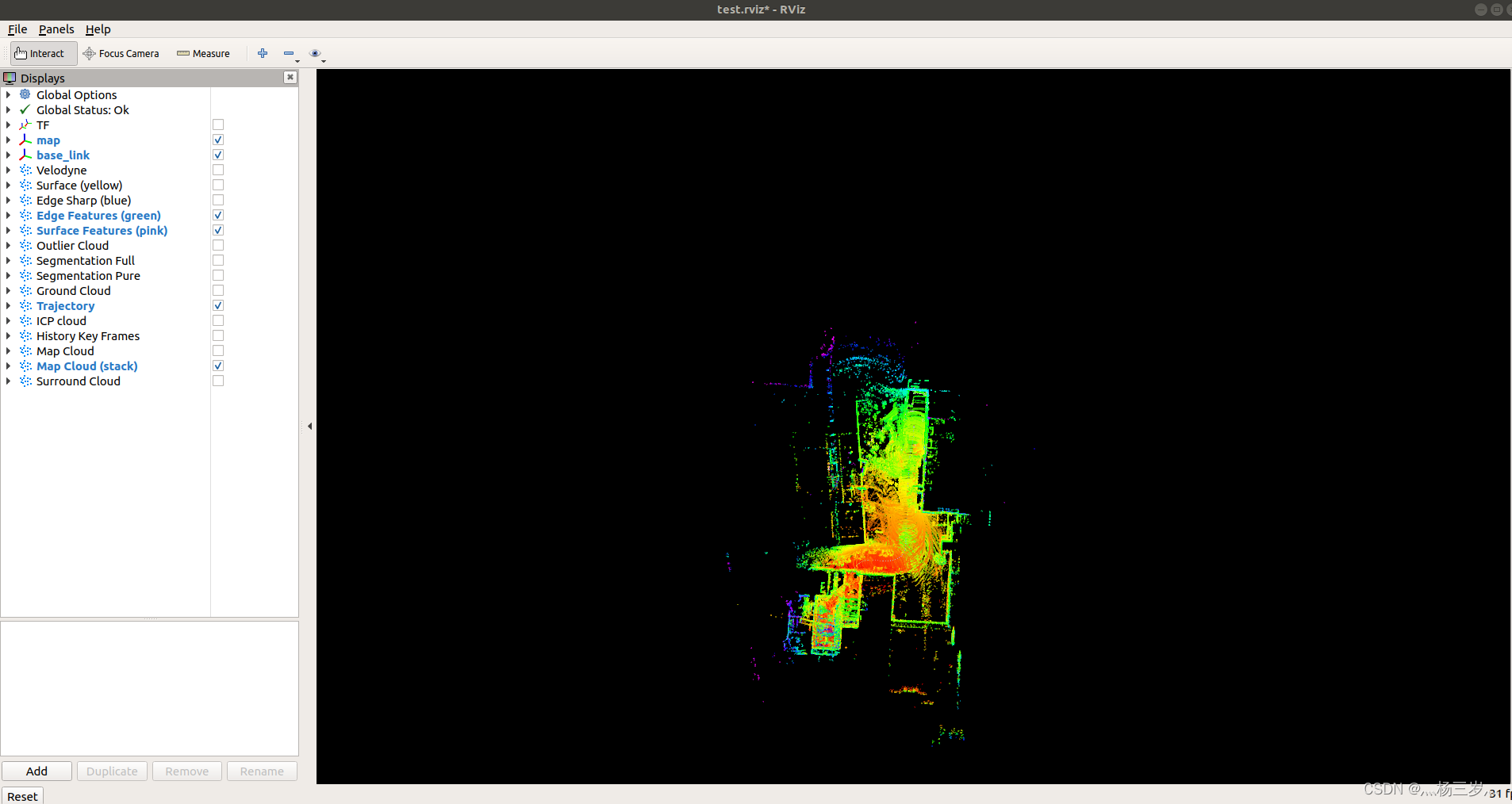
Ubuntu18.04安装LeGO-LOAM保姆级教程
系统环境:Ubuntu18.04.6 LTS 1.LeGO-LOAM的安装前要求: 1.1 ROS安装:参考我的另一篇博客Ubuntu18.04安装ROS-melodic保姆级教程_灬杨三岁灬的博客-CSDN博客文章浏览阅读168次。Ubuntu18.04安装ROS-melodic保姆级教程https://blog.csdn.net/…...
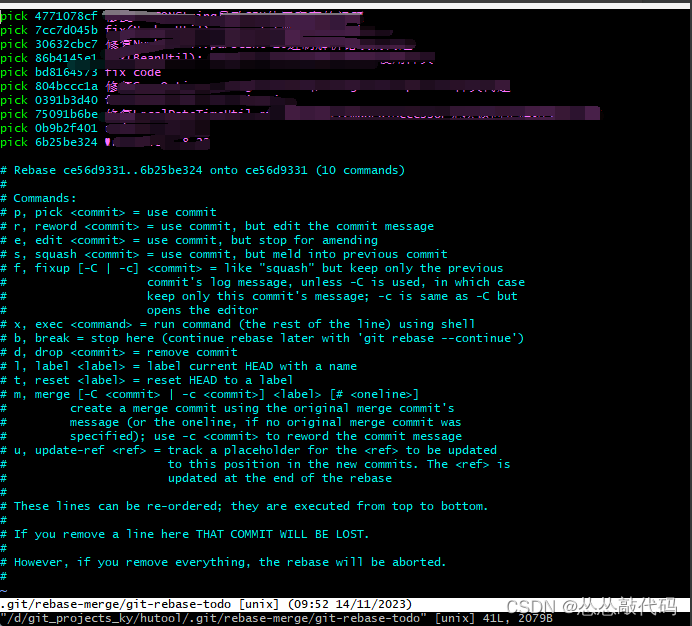
git修改commit历史提交时间、作者
1、修改最近的几条记录,进入提交记录列表,修改提交记录模式 git rebase -i HEAD~3 // 修改最近的三条记录,顺序排列按提交时间升序 指令说明: pick:保留该commit(缩写:p) reword:…...
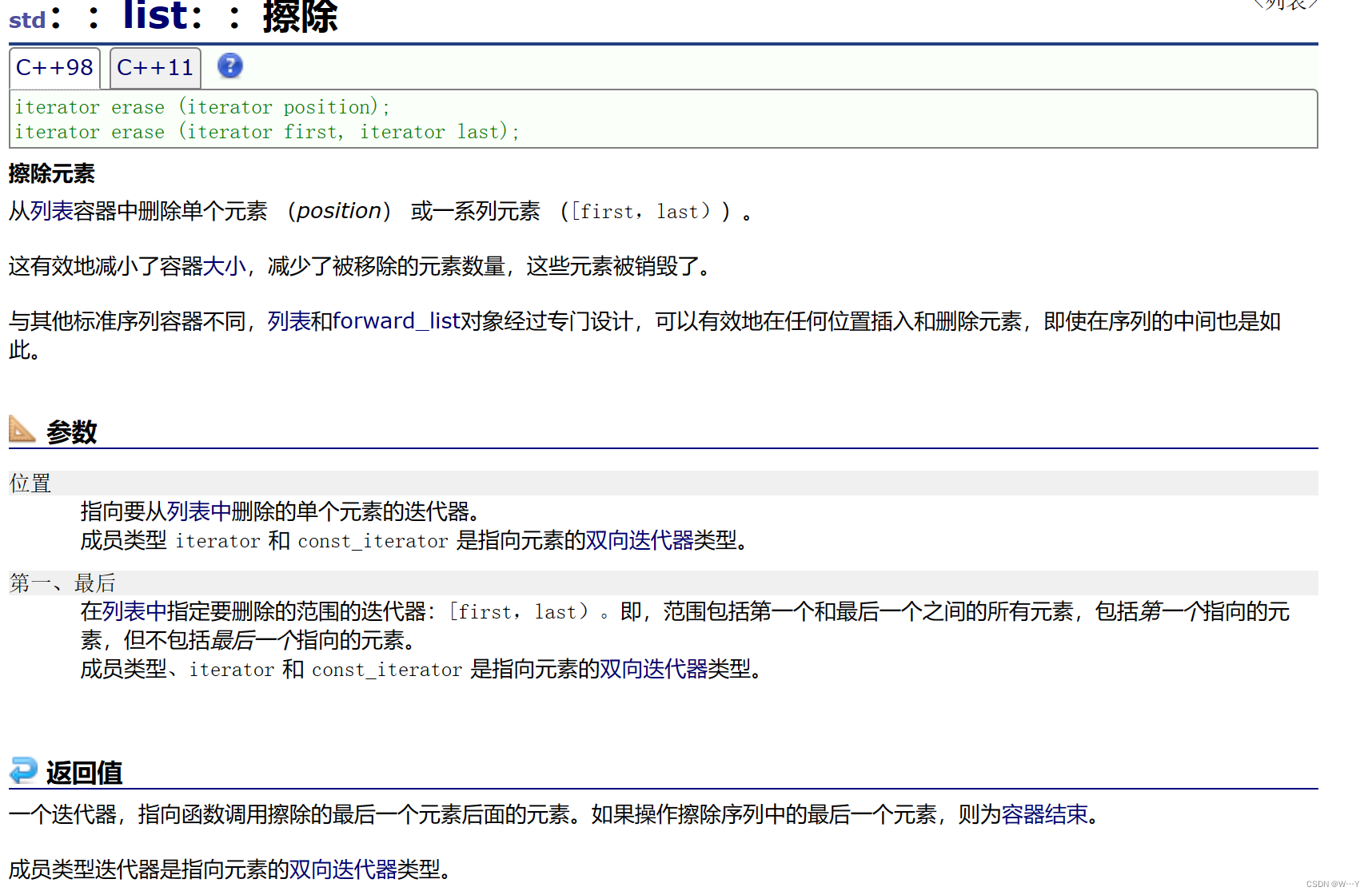
【C++历练之路】list的重要接口||底层逻辑的三个封装以及模拟实现
W...Y的主页 😊 代码仓库分享💕 🍔前言: 在C的世界中,有一种数据结构,它不仅像一个神奇的瑰宝匣,还像一位能够在数据的海洋中航行的智慧舵手。这就是C中的list,一个引人入胜的工具…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
