git常常用命令
这篇文章中,一些简单的,大家都知道的git 命令我就不再赘述,我只写出来最近在项目中常用到的一些命令。这些命令可以帮助我更好的开发。
git stash
请大家设想下面的场景,你的本地有两个分支,develop,fix分支,你正在develop分支上写一些需求,但是还没有写好,突然来了一个很紧急的bug,这个bug需要你切换到fix分支进行修改。此时你会怎样?是把未开发完毕的需求commit吗?还是直接变更分支?直接commit会导致本地的提交非常的乱。直接变更分支,那你未开发完毕的代码可就离你而去了……
你有更好的选择。git stash 可以帮助你先将没开发完毕的需求放到暂存区中,允许你切换到其他分支修改完毕后,切回原先的分支并恢复。这样你就可以重新开发了。
使用:
1.git stash
保存当前工作进度,会把暂存区和工作区的改动保存起来。执行完这个命令后,在运行git status命令,就会发现当前是一个干净的工作区,没有任何改动。使用git stash save 'message...'可以添加一些注释
2.git stash list
显示保存进度的列表。也就意味着,git stash命令可以多次执行。
3.git stash pop [–index] [stash]
git stash pop 恢复最新的进度到工作区。git默认会把工作区和暂存区的改动都恢复到工作区。
git stash pop --index 恢复最新的进度到工作区和暂存区。(尝试将原来暂存区的改动还恢复到暂存区)
git stash pop stash@{1}恢复指定的进度到工作区。stash_id是通过git stash list命令得到的
通过git stash pop命令恢复进度后,会删除当前进度。
4.git stash apply [-index] [stash_id]
通过git stash apply命令恢复进度后,不会删除当前进度,其余和git stash pop 一样
5.git stash drop [stash_id]
删除一个存储的进度。如果不指定stash_id,则默认删除最新的存储进度。
6.git stash clear
清除所有存储的进度
commit后再撤销commit
当你commit修改了一些代码后,提交到本地了。后来又发现有更好的解决办法,但是此时本地已经有一版commit了,为了保证工作树的清晰,尽量不要commit两次。那么此时如何撤回之前的commit
git reset --soft HEAD^ 这样就成功撤销了commit,如果想要连着add也撤销的话,–soft改为–hard(删除工作空间的改动代码)。
命令详解:
HEAD^ 表示上一个版本,即上一次的commit,也可以写成HEAD~1
如果进行两次的commit,想要都撤回,可以使用HEAD~2
–soft
不删除工作空间的改动代码 ,撤销commit,不撤销git add file
–hard
删除工作空间的改动代码,撤销commit且撤销add
add 后取消指定文件add
当我们不小心 git add . 将所有更新都提到仓库后,想撤销操作。
这时候可以用
git reset .将所有add 上的东西全部取消提交,然后再提交指定文件
或者先用 git status 查看提交了哪些文件,然后 git reset + 指定文件 来撤回。
git cherry-pick
在项目中,往往我们会有很多个分支,当我们发现多个分支中存在同样的问题时,这时候我们就可以只在一个分支上进行修改,然后利用cherry-pick 命令将指定的新提交合入另一个分支上。
git cherry-pick 提交号

利用这个命令就可以实现将指定提交合入分支的操作了。
相关文章:

git常常用命令
这篇文章中,一些简单的,大家都知道的git 命令我就不再赘述,我只写出来最近在项目中常用到的一些命令。这些命令可以帮助我更好的开发。 git stash 请大家设想下面的场景,你的本地有两个分支,develop,fix分支…...

C语言中的大端字节序和小端字节序是什么?如何进行字节序的转换?
C语言中的大端字节序和小端字节序以及字节序的转换 引言 在计算机科学中,字节序是指多字节数据在存储或传输过程中字节的排列顺序。在C语言中,特别是在涉及二进制数据的处理、网络通信以及硬件相关的编程中,了解大端字节序和小端字节序的概…...

Flutter dio Http请求之Cookie管理
在应用开发过程中,我们进行Http通讯时会使用Cookie进行验证,今天我们就着重讲解Flutter 网络请求插件dio的cookie使用。 首先,我们要进行插件引用 # HTTP 请求 dio: ^5.1.1 cookie_jar: ^4.0.8 dio_cookie_manager: ^3.0.0# 获取沙盒路径 p…...
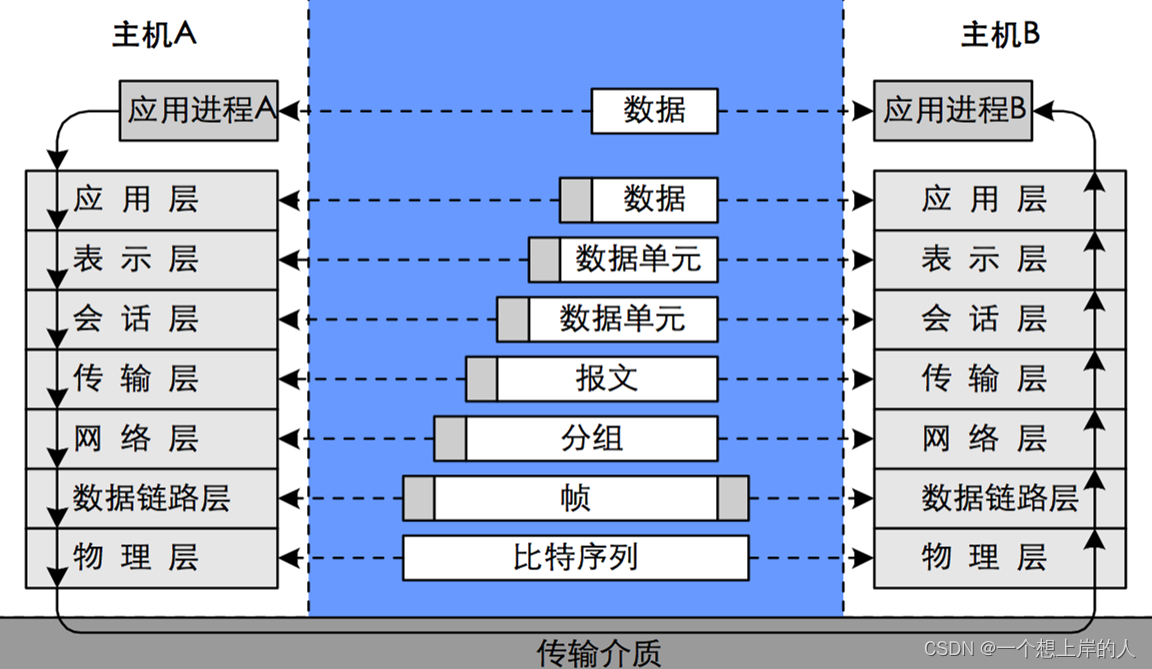
计算机网络的标准化工作及相关组织
一、国际化组织 计算机网络的标准化工作由一些主要的组织来进行管理和推动。以下是几个主要的计算机网络标准化的国际组织及其相关的标准: 1. 国际标准化组织(ISO):国际标准化组织负责制定各种行业的标准,包括计算机…...

智能座舱架构与芯片- (11) 软件篇 上
一、智能汽车基础软件平台分类 汽车软件主要分为应用软件和基础软件。应用软件和业务形态高度关联,不同控制器的应用软件之间差异较大。基础软件介于应用软件和硬件之间,用于屏蔽硬件特性、支撑应用软件。可有效地实现应用软件与硬件之间解耦࿰…...
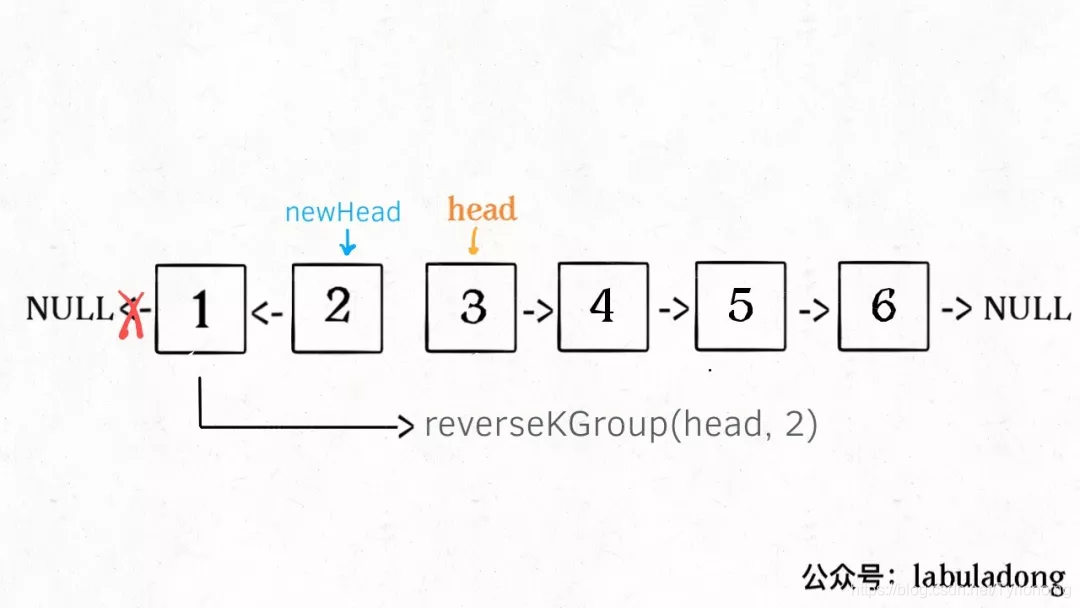
2021秋招-算法-递归
算法-递归 教程: ⭐告别递归,谈谈我的一些经验 LeetCode刷题总结-递归篇 基础框架 leetcode刷题 1.leetcode-101. 对称二叉树-简单 101. 对称二叉树 给定一个二叉树,检查它是否是镜像对称的。 例如,二叉树 [1,2,2,3,4,4,3] 是对称的。…...

【Django-02】 Model模型和模型描述对象Meta
Model和Meta 概念ModelMetaModel支持的字段类型Meta 属性例子 概念 就是对象的意思,底层一个Model对应一张表,而Meta是Model的内部类,是用来描述Model和数据库表的相关元数据信息,比如主键,排序,unique_ke…...
-java)
【华为OD题库-030】阿里巴巴找黄金宝箱(V)-java
题目 一贫如洗的樵夫阿里巴巴在去砍柴的路上,无意中发现了强盗集团的藏宝地,藏宝地有编号从0-N的箱子,每个箱子上面贴有一个数字.阿里巴巴念出一个咒语数字k(k<N),找出连续k个宝箱数字和的最大值,并输出该最大值。 输入描述 第…...
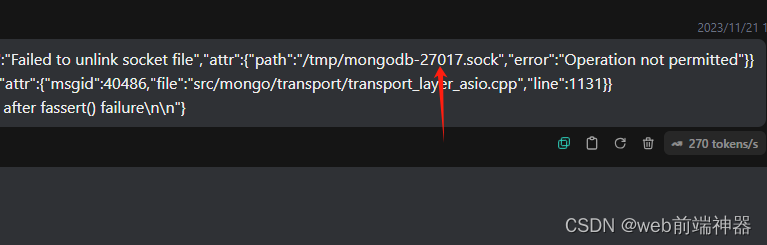
centos7卸载mongodb数据重新安装时无法安装的问题
如果卸载不干净直接用 sudo find / -name mongo 查询所有关于mongo的文件,然后一个个去删除。 当然最好的办法还是去看日志信息。 直接去查看日志信息 sudo cat /var/log/mongodb/mongod.log 根据提示信息说这个没有权限操作 直接删除即可,都是之前…...

ES6 的 class 类和Typescript 的 class 类的区别
前言 为什么要理解ES6的类和TS类的区别: 都是面向对象的开发它们看着很像但是它们不一样学习明白了,避免混用 ES6 类是 JavaScript 中基于原型的面向对象编程的语法糖,而 TypeScript 类在此基础上增加了强类型检查和其他面向对象编程的特性…...

Android 12.0 默认授予应用权限
Android 12.0 默认授予应用权限 最近接到客户需求提到每当首次点开某个应用时都会弹出申请权限的弹窗,操作起来感觉很麻烦,需要将指定的这个应用默认授予权限,具体修改参照如下: frameworks/base/services/core/java/com/androi…...
——多源遥感变量筛选(PCA主成分分析),变量筛选/降维处理)
Google Earth Engine(GEE)——多源遥感变量筛选(PCA主成分分析),变量筛选/降维处理
简介 很多时候我们需要进行数据的将为和筛选,传统的方法我们可以根绝经验方法进行筛选或者按照变量重要性和相关性进行分析,当然我们可以通过计算多个变量之间的主成分分析来进行变量的筛选,本文已森林生物量分析作为自变量,其它多源遥感变量作为相关性因变量,进行分类对…...

爬虫的http和https基础
HTTP响应状态码响应状态码 下面来看下详细的状态码数值和说明: 200系列: 200 OK:这个是最常见的,也是爬虫工程师最喜欢的,代表你本次的请求顺利拿到了响应,没有任何问题 201 Created:201代表…...
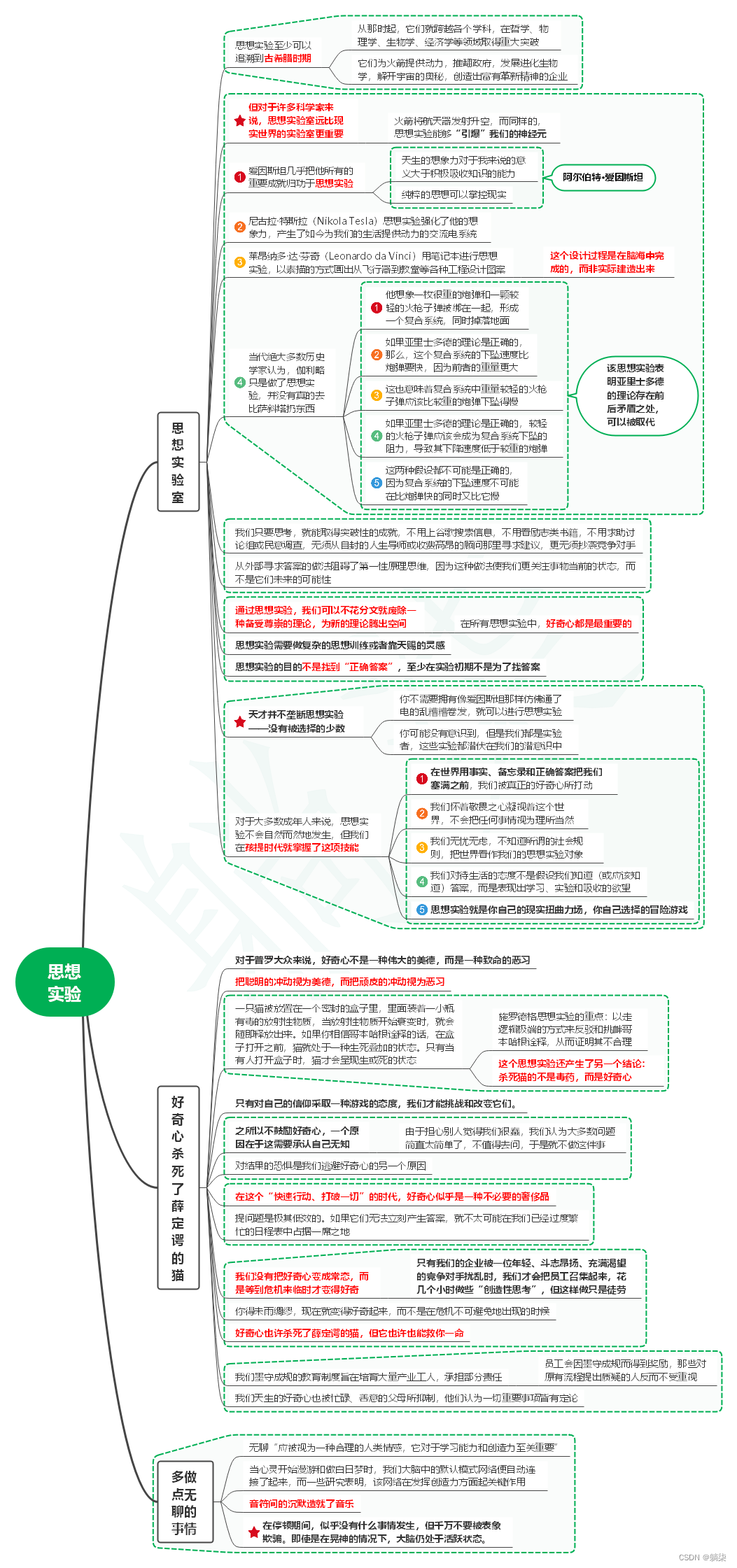
读像火箭科学家一样思考笔记05_思想实验
1. 思想实验室 1.1. 思想实验至少可以追溯到古希腊时期 1.1.1. 从那时起,它们就跨越各个学科,在哲学、物理学、生物学、经济学等领域取得重大突破 1.1.2. 它们为火箭提供动力,推翻政府,发展进化生物学,解开宇宙的奥…...

mac gitee新建工程遇到的一些问题
首先,记录一下mac系统显示隐藏文件夹的快捷键:commandshift句号,可以显示工程目录下的隐藏的git文件夹 一 git报错:‘origin‘does not appear to be a git repository的解决方法 找到工程目录下的.git/config文件发现里边没有remote orig…...
某60区块链安全之Call函数簇滥用实战一学习记录
区块链安全 文章目录 区块链安全Call函数簇滥用实战一实验目的实验环境实验原理实验内容实验过程 Call函数簇滥用实战一 实验目的 学会使用python3的web3模块 学会以太坊Delegatecall漏洞分析及利用 实验环境 Ubuntu18.04操作机 实验工具 python3 实验原理 call 外部调用…...
最新AIGC创作系统ChatGPT系统源码,支持最新GPT-4-Turbo模型,支持DALL-E3文生图,图片对话理解功能
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如…...
)
openssl+ SM2 + linux 签名开发实例(C++)
文章目录 一、SM2 签名理论基础二、SM2签名开发实例 一、SM2 签名理论基础 SM2是中国国家密码管理局发布的椭圆曲线密码算法标准,用于数字签名、密钥交换和公钥加密等安全通信场景。以下是SM2签名的理论基础相关知识点: 椭圆曲线密码学(Elli…...
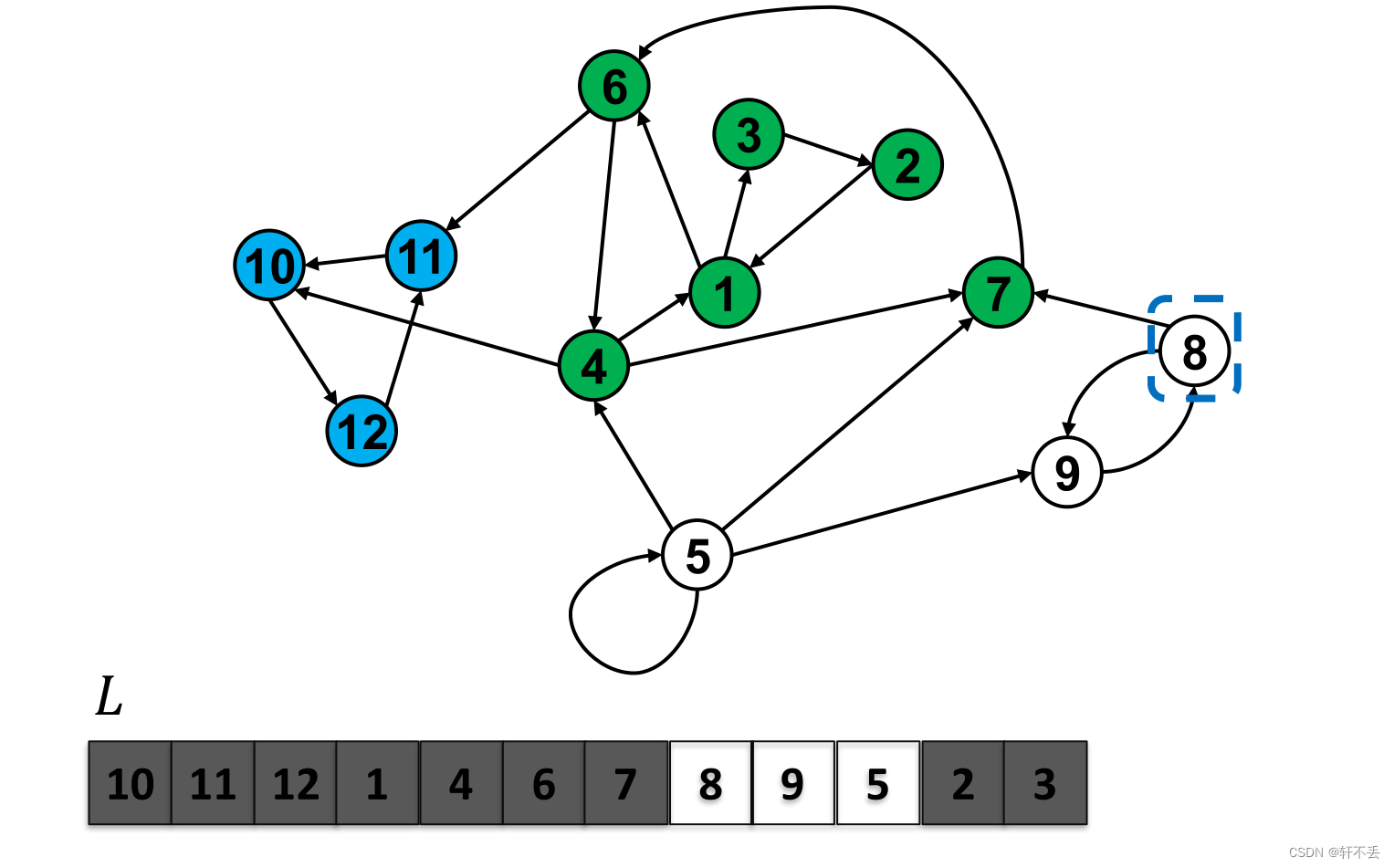
U4_1:图论之DFS/BFS/TS/Scc
文章目录 一、图的基本概念二、广度优先搜索(BFS)记录伪代码时间复杂度流程应用 三、深度优先搜索(DFS)记录伪代码时间复杂度流程时间戳结构BFS和DFS比较 四、拓扑排序一些概念有向图作用拓扑排序 分析伪代码时间复杂度彩蛋 五、强…...

STM32框架之按键扫描新思路
STM32框架之按键扫描新思路 引入代码展示思路分析 我们学习了定时器实现毫秒级/秒级任务框架,这期我们基于任务框架学习按键扫描新思路。 引入 在按键扫描的过程中,最重要的一步就是按键消抖,解决的方法最简单粗暴的就是先扫描一次按键状态&…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
