U4_1:图论之DFS/BFS/TS/Scc
文章目录
- 一、图的基本概念
- 二、广度优先搜索(BFS)
- 记录
- 伪代码
- 时间复杂度
- 流程
- 应用
- 三、深度优先搜索(DFS)
- 记录
- 伪代码
- 时间复杂度
- 流程
- 时间戳结构
- BFS和DFS比较
- 四、拓扑排序
- 一些概念
- 有向图
- 作用
- 拓扑排序
- 分析
- 伪代码
- 时间复杂度
- 彩蛋
- 五、强连通分量-SCC
- 分析
- 伪代码
- 时间复杂度
一、图的基本概念
由点(vertices)和边(edges)组成
G = ( V , E ) G=(V,E) G=(V,E), ∣ V ∣ = n |V|=n ∣V∣=n, ∣ E ∣ = m |E|=m ∣E∣=m (这里默认有向图,无向图用 G G G = = ={ V V V, E E E}表示
顶点的度是关联在其上的边的数量。满足 ∑ d e g r e e ( v ) = 2 ∣ E ∣ \sum degree(v)=2|E| ∑degree(v)=2∣E∣(握手定理)
路径:一个序列 < V 0 , V 1 , . . . , V k > <V_0,V_1,...,V_k> <V0,V1,...,Vk>且 i = 1 , 2 , . . . , k i=1,2,...,k i=1,2,...,k满足 ( V i − 1 , V i ) (V_{i-1},V_i) (Vi−1,Vi),序列中任意两点之间都是可达的。
简单路径:序列中所有顶点都是不同的。
环:一个路径 < V 0 , V 1 , . . . , V k > <V_0,V_1,...,V_k> <V0,V1,...,Vk>并且 V 0 = V k V_0=V_k V0=Vk并且路径上所有边都是不同的
简单环: V 1 , V 2 , . . . , V k V_1,V_2,...,V_k V1,V2,...,Vk是不同的。
连通:两个点之间存在路径。每个顶点对之间都连通,则这个图是连通的
连通分量:两点之间连通的最大集合的个数(等价类)。如下图:
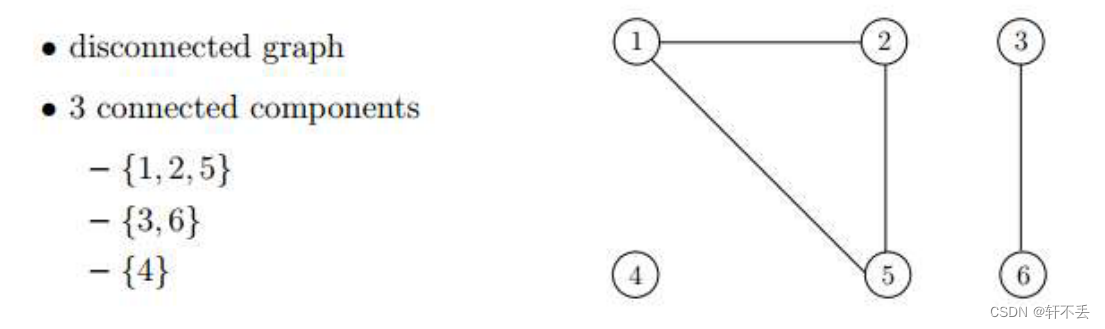
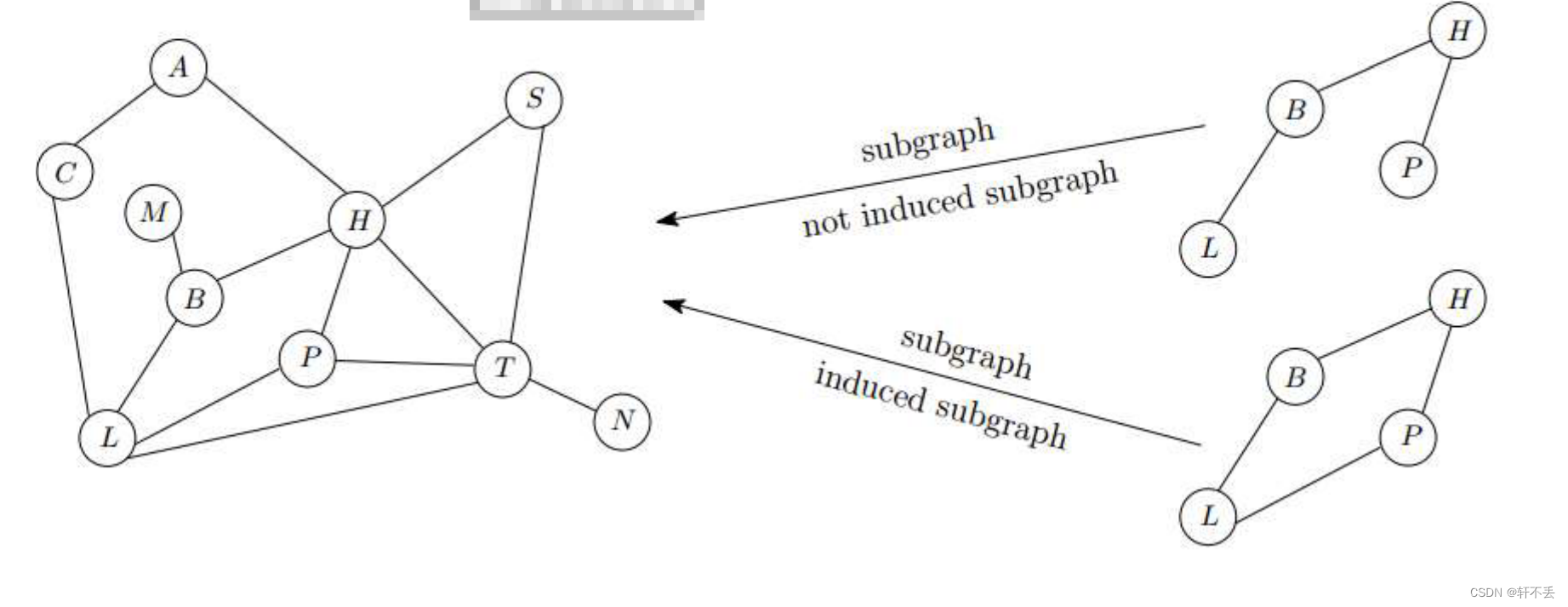
子图: G ′ G' G′的点和边都属于 G G G
诱导子图: G ′ G' G′的点属于 G G G,且连接点的所有边都要属于 G ′ G' G′
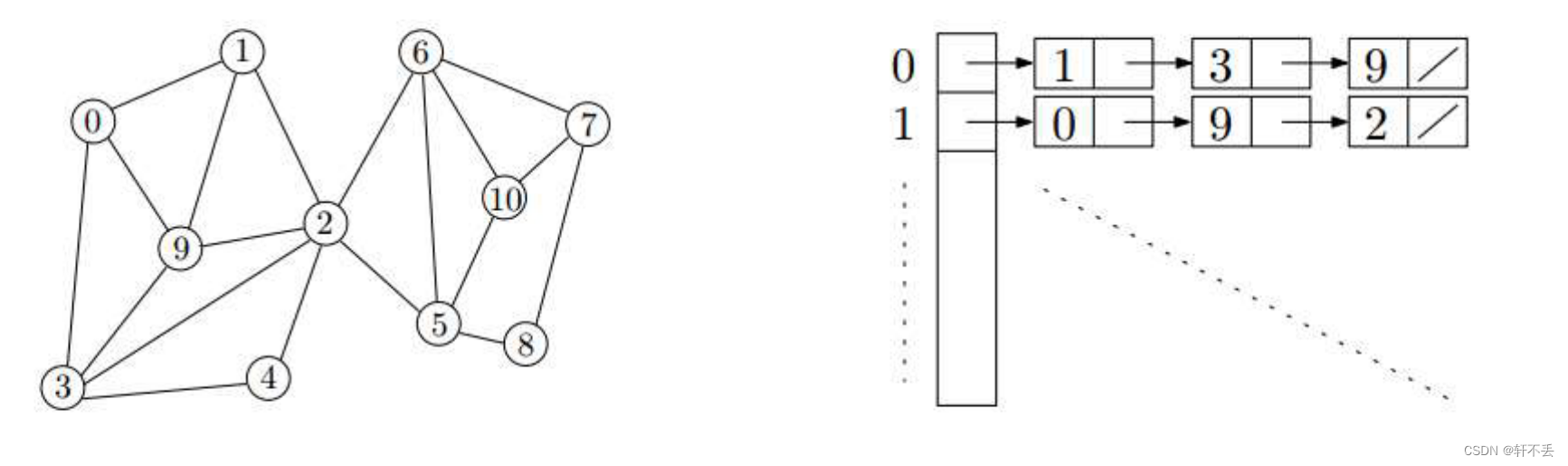
邻接表Adj:用链表连接每个点的边。因此是遍历了每个点和每条边,因此时间复杂度 T ( n ) = O ( V + E ) T(n)=O(V+E) T(n)=O(V+E)
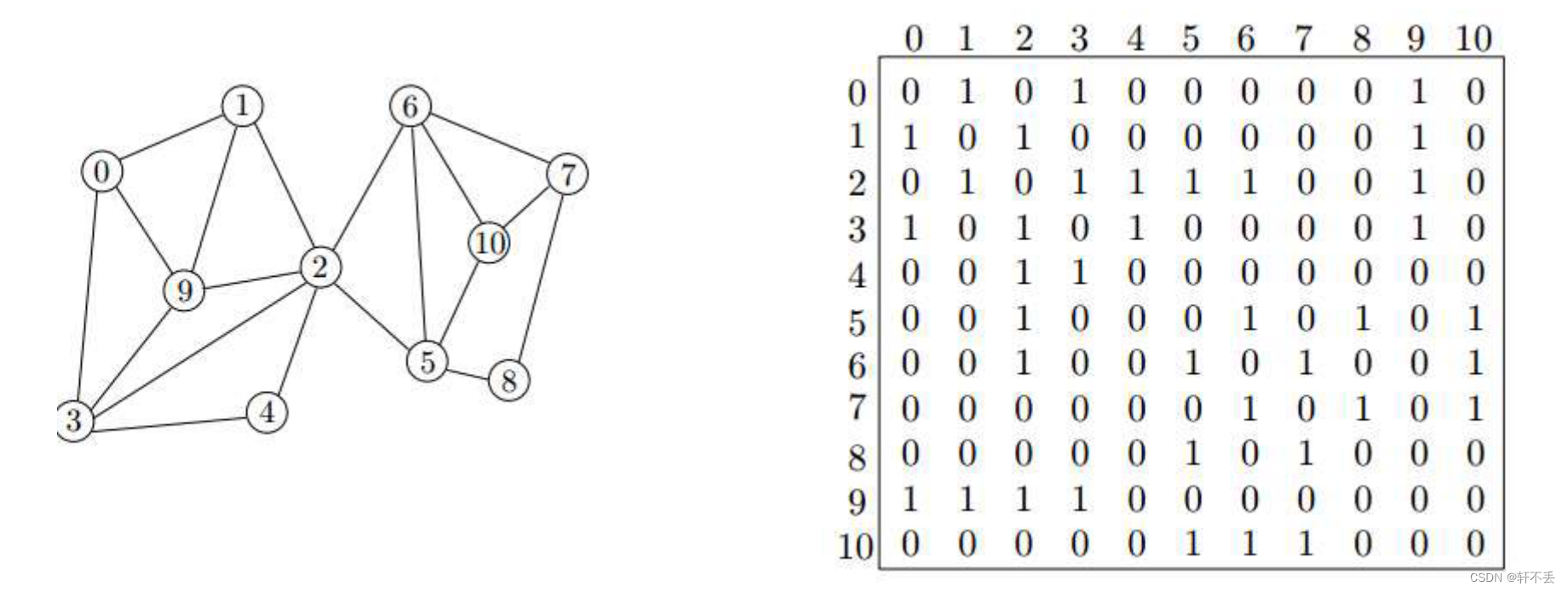
邻接矩阵: A = [ a i j ] , a i j = 1 A=[a_{ij}],a_{ij}=1 A=[aij],aij=1 i f ( v i , v j ) 属于 E if(v_i,v_j)属于E if(vi,vj)属于E,否则 a i j = 0 a_{ij}=0 aij=0
因为不管怎样任意两点间有无边都要判断一遍,因此时间复杂度 T ( n ) = O ( V 2 ) T(n)=O(V^2) T(n)=O(V2)
二、广度优先搜索(BFS)
用处:遍历图中的所有顶点,从而显示图的属性
记录
三个数组用于保存遍历期间收集的信息。
- c o l o r [ u ] color[u] color[u]:访问的每个顶点的颜色
W H I T E WHITE WHITE:未发现
G R A Y GRAY GRAY:已发现但未完成处理
B L A C K BLACK BLACK:已完成处理 - p r e d [ u ] pred[u] pred[u]:前一个指针:指向发现u的顶点
- d [ u ] d[u] d[u]:从源到顶点u的距离
伪代码
BFS(G)
for u in V docolor[u] ← WHITE;pred[u] ← NULL;
end
for u in V doif color[u] is equal to WHITE thenBFSVisit(u);end
endBFSVisit(s)
color[s] ← GRAY,d[s] ← 0;
set Q a queue
Enqueue(Q,s)
while Q is not empty dou ← Dequeue(Q)for v is belong to Adj[u] do (邻接表遍历的)if(color[v] = WHITE) thencolor[u] ← GRAYd[v] ← d[u]+1pred[v] ← uEnqueue(Q,v)endendcolor[u] ← BLACK
end
时间复杂度
每一次循环遍历,都是遍历一个点和其边,且边遍历过了其他边就不会再遍历,因此
T ( n ) = ∑ O ( 1 + d e g r e e ( u ) ) = O ( V + E ) T(n)=\sum O(1+degree(u))=O(V+E) T(n)=∑O(1+degree(u))=O(V+E)
流程
一次BFSVisit,能将连通分量遍历完

应用
- 最短路径问题
- 查找连通分量
三、深度优先搜索(DFS)
用处:同样也是遍历图中的所有顶点,从而显示图的属性
记录
四个数组用于保存遍历期间收集的信息。
- c o l o r [ u ] color[u] color[u]:访问的每个顶点的颜色
W H I T E WHITE WHITE:未发现
G R A Y GRAY GRAY:已发现但未完成处理
B L A C K BLACK BLACK:已完成处理 - p r e d [ u ] pred[u] pred[u]:前一个指针:指向发现u的顶点
- d [ u ] d[u] d[u]:发现时间。(设置一个全局变量时间发生器)
- f [ u ] f[u] f[u]:结束时间。一个计数器,指示顶点u(及其所有后代)的处理何时完成
伪代码
DFS(G)
for u in V docolor[u] ← WHITE;pred[u] ← NULL;
endtime ← 0
for u in V doif color[u] is equal to WHITE thenDFSVisit(u);end
endDFSVisit(u)
color[u] ← GRAY,d[u] ← ++time;
set Q a queue
Enqueue(Q,s)
for v is belong to Adj[u] do (邻接表遍历的)if(color[v] = WHITE) thenpred[v] ← uDFSVisit(v)end
end
color[u] ← BLACK
f[u] ← ++time;
时间复杂度
同样,每一次循环遍历,都是遍历一个点和其边,且边遍历过了其他边就不会再遍历,因此
T ( n ) = ∑ O ( 1 + d e g r e e ( u ) ) = O ( V + E ) T(n)=\sum O(1+degree(u))=O(V+E) T(n)=∑O(1+degree(u))=O(V+E)
流程
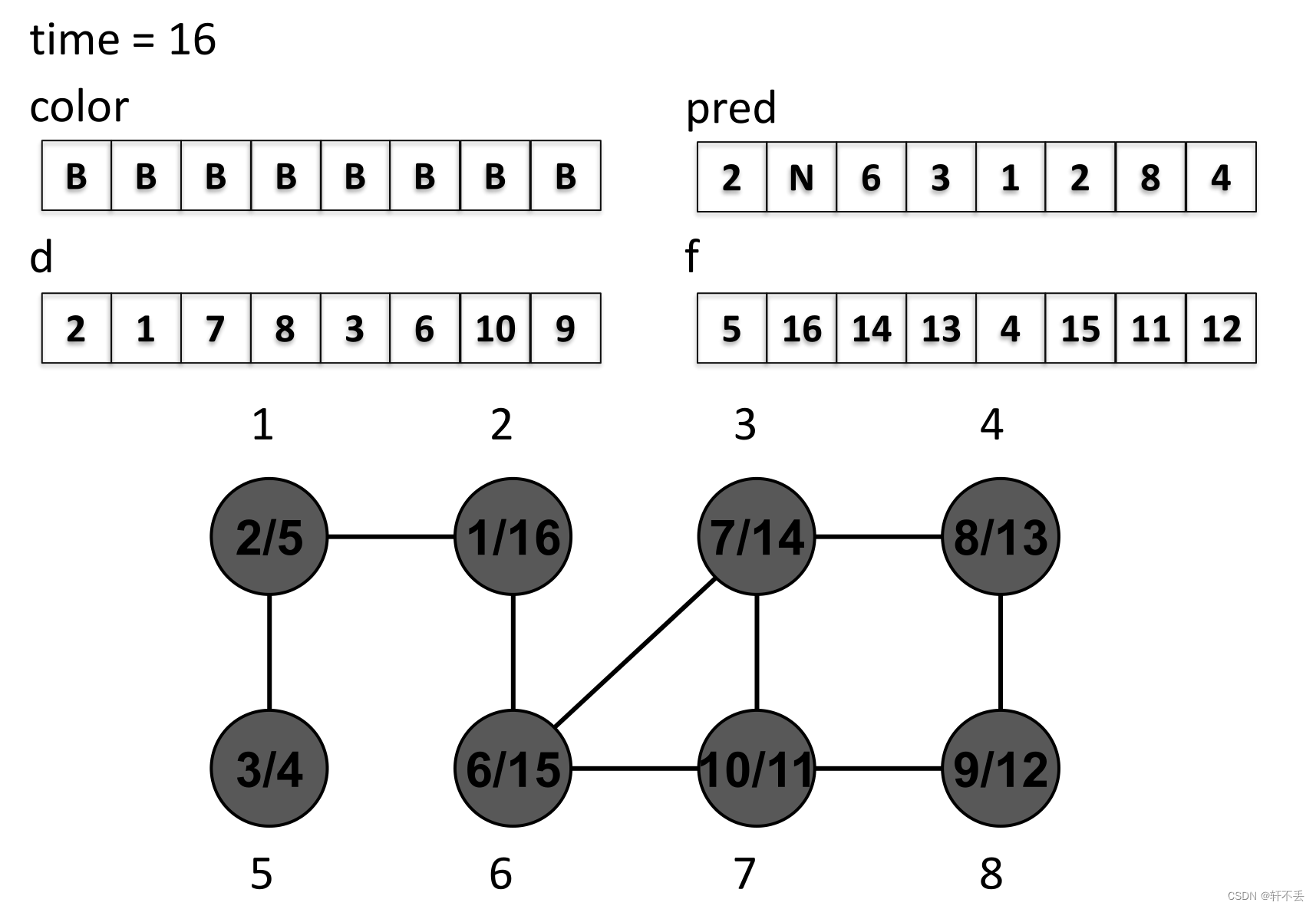
时间戳结构
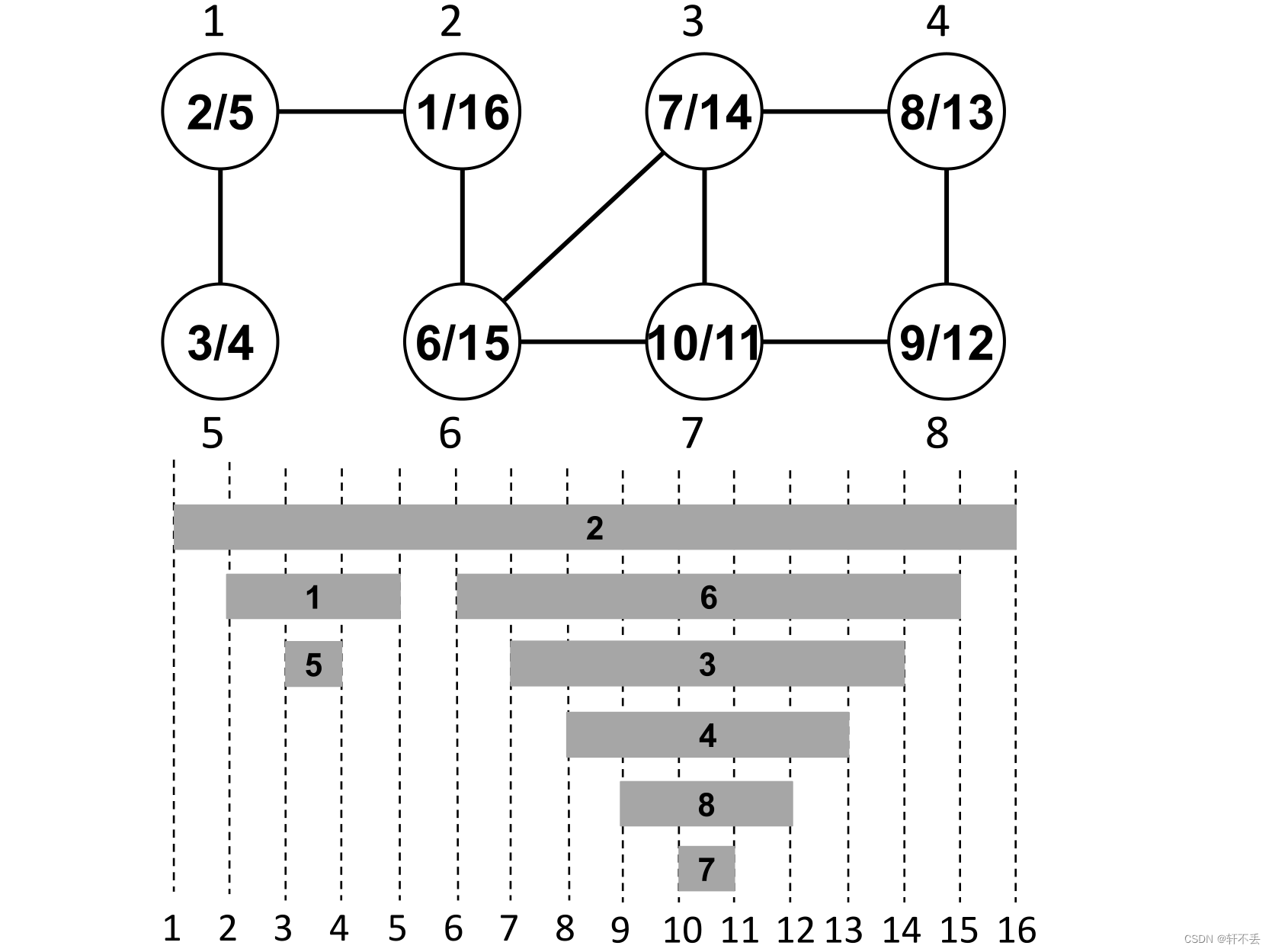
由图可知, u u u是 v v v的后代(在 D F S DFS DFS树中),当且仅当 [ d [ u ] , f [ u ] ] [d[u],f [u]] [d[u],f[u]]是 [ d [ v ] , f [ v ] ] [d[v],f [v]] [d[v],f[v]]的子区间
树边: i f ( u , v ) ∈ E f if (u, v)∈E_f if(u,v)∈Ef等价 u = p r e d [ v ] u = pred[v] u=pred[v],即 u u u是 D F S DFS DFS树中 v v v的前身(图中蓝色边)
后边缘:如果 v v v是 D F S DFS DFS树中 u u u的祖先(不包括前身)(图中红色边)
有边就有祖先和后代的关系

BFS和DFS比较
BFS是发现点之后先处理,DFS是发现点之后不处理,继续往下去找其他的点。
四、拓扑排序
一些概念
有向图
有向图,区分边(u, v)和边(v, u)
顶点的出界度是离开它的边的数量,顶点的入界度是进入它的边的数量
每条边(u, v)对u的出阶贡献1次,对v的入阶贡献1次
∑ o u t − d e g r e e ( v ) = ∑ i n − d e g r e e ( v ) = ∣ E ∣ \sum out-degree(v)=\sum in-degree(v)=|E| ∑out−degree(v)=∑in−degree(v)=∣E∣
作用
有向图通常用于表示顺序相关的任务,也就是说,我们不能在另一个任务完成之前启动一个任务。
边(u, v)表示任务u完成后才能启动任务v。
显然,要使系统不挂起,图必须是无环的,它必须是有向无环图(或DAG)
拓扑排序
拓扑排序是一种针对有向无环图的算法,对顶点进行线性排序,使得对于DAG中的每条边(u, v), u在线性排序中出现在v之前。
它可能不是唯一的,因为有许多“不兼容”的元素。
分析
- 起始顶点入度必须为0,如果这样的顶点不存在,图就不是无环的。
- 一个入度为0的顶点是一个可以马上开始的任务。所以我们可以先以线性顺序输出它.
- 如果输出一个顶点u,那么所有的边(u, v)都不再有用,因为任务v不再需要等待u。
- 去掉顶点u后,新图仍然是一个有向无环图
- 重复步骤2-4,直到没有顶点留下
伪代码
Initialize Q to be an empty queue
for u is belong to V do thenif u.in_degree is equal to 0 thenEnqueue(Q,u)end
end
while Q is not empty dou ← Dequeue(Q)Output u;for v is belong to Adj(u) dov.in_degree ← v.in_degree-1if v,in_degree is equal to 0 thenEnqueue(Q,v)endend
end
时间复杂度
依旧是每条边和每个顶点都遍历一遍,因此时间复杂度 T ( n ) = O ( V + E ) T(n)=O(V+E) T(n)=O(V+E)
彩蛋
也可用DFS求出拓扑序列,对于每个有向边,都有 f [ u ] > f [ v ] f[u]>f[v] f[u]>f[v]
在时间O(V+E)内计算出 D A G DAG DAG(有向无环图)中的单源最短路径:动态规划
五、强连通分量-SCC
任意两点之间都有路径,再增加一个点都不满足这个关系。
任何两个强连通分量交集都为空
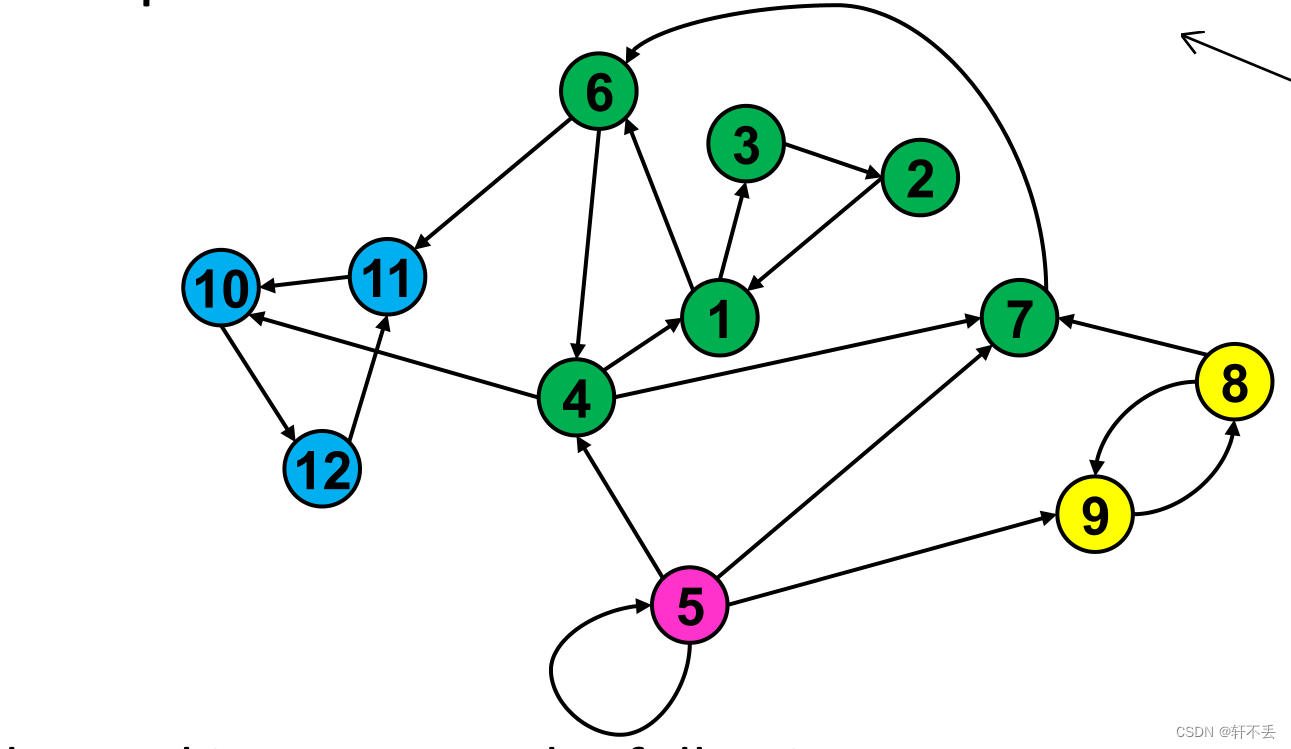
找到一个算法,求一个图得所有连通分量
分析
- 对G中所有边的方向进行反转,得到逆图GR。
- 执行DFS,并获得GR中顶点变黑的序列,即每当一个顶点从堆栈中弹出时,将其附加到序列 L R L^R LR中,将 L R L^R LR倒序得到序列L
- 对原图G执行DFS,规则如下
规则1:从L的第一个顶点开始DFS
规则2:当需要重新开始时,从L的第一个仍然是白色的顶点开始
将每个dfs树中的顶点输出为SCC
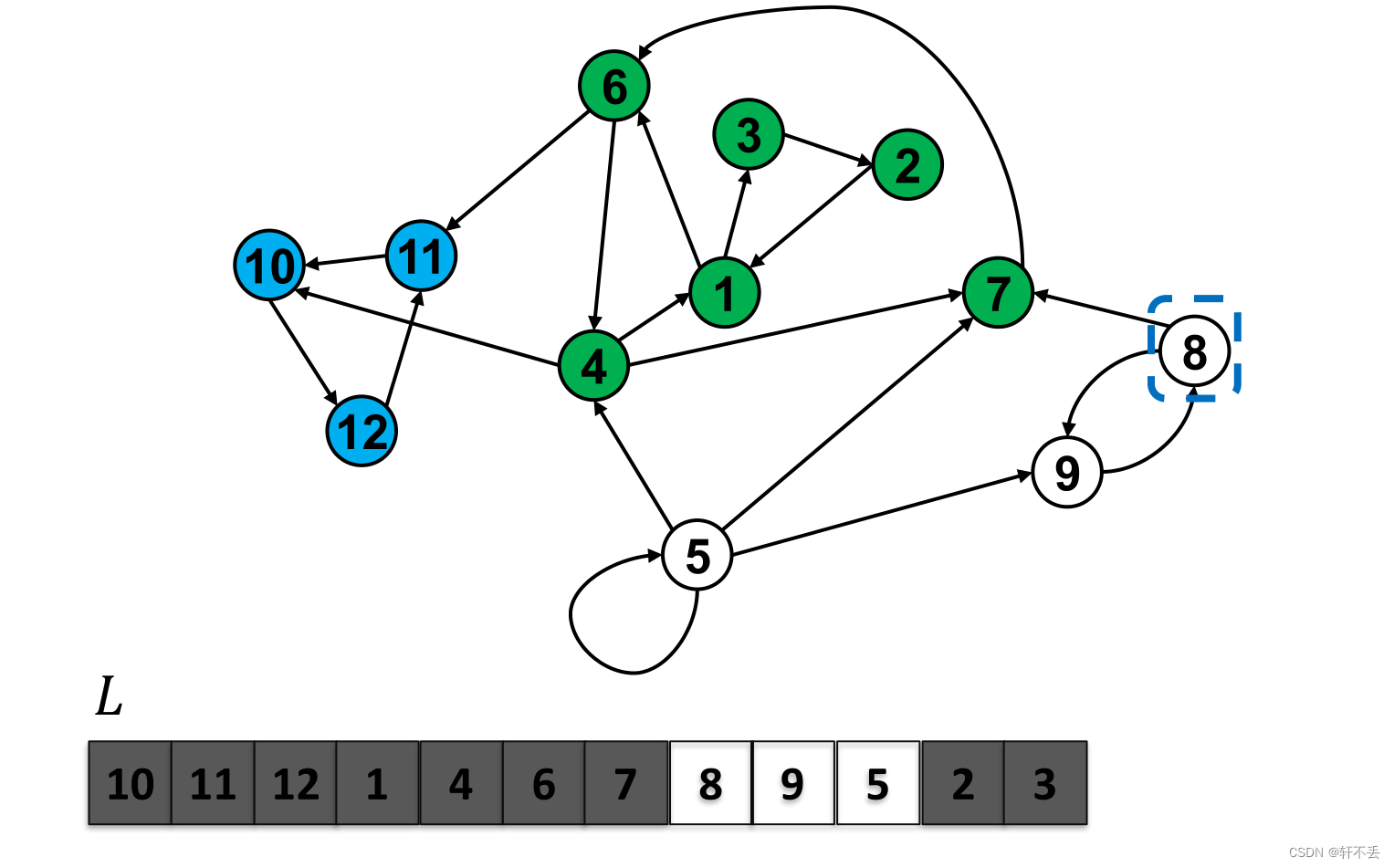
伪代码
R ← {}
Reverse G and get G'
DFS G' and get L'
reverse L' and get L
for u属于L doif color[u] is WHITE thenLscc ← DFSVisit(G,u)R ← RUSet(Lscc)end
end
时间复杂度
翻转边需要遍历每个点和边,时间复杂度为 O ( V + E ) O(V+E) O(V+E),DFS时间复杂度为 O ( V + E ) O(V+E) O(V+E),,然后还是依次遍历每个点和边,时间复杂度也是 O ( V + E ) O(V+E) O(V+E),因此总时间复杂度为 T ( n ) = O ( V + E ) T(n)=O(V+E) T(n)=O(V+E)
相关文章:

U4_1:图论之DFS/BFS/TS/Scc
文章目录 一、图的基本概念二、广度优先搜索(BFS)记录伪代码时间复杂度流程应用 三、深度优先搜索(DFS)记录伪代码时间复杂度流程时间戳结构BFS和DFS比较 四、拓扑排序一些概念有向图作用拓扑排序 分析伪代码时间复杂度彩蛋 五、强…...

STM32框架之按键扫描新思路
STM32框架之按键扫描新思路 引入代码展示思路分析 我们学习了定时器实现毫秒级/秒级任务框架,这期我们基于任务框架学习按键扫描新思路。 引入 在按键扫描的过程中,最重要的一步就是按键消抖,解决的方法最简单粗暴的就是先扫描一次按键状态&…...
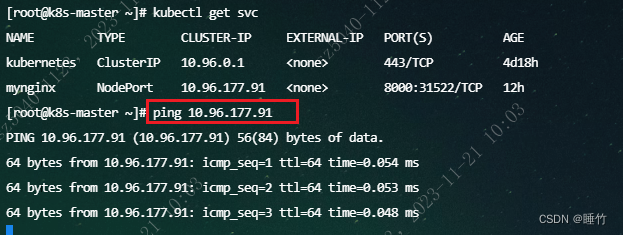
完美解决k8s master节点无法ping node节点中的IP或Service NodePort的IP
1、问题一 使用搭建好了K8S集群,先是node节点加入k8s集群时,用的内网IP,导致master节点无法操作node节点中的pod(这里的不能操作,指定是无法查看node节点中pod的日志、启动描述、无法进入pod内部,即 kubec…...
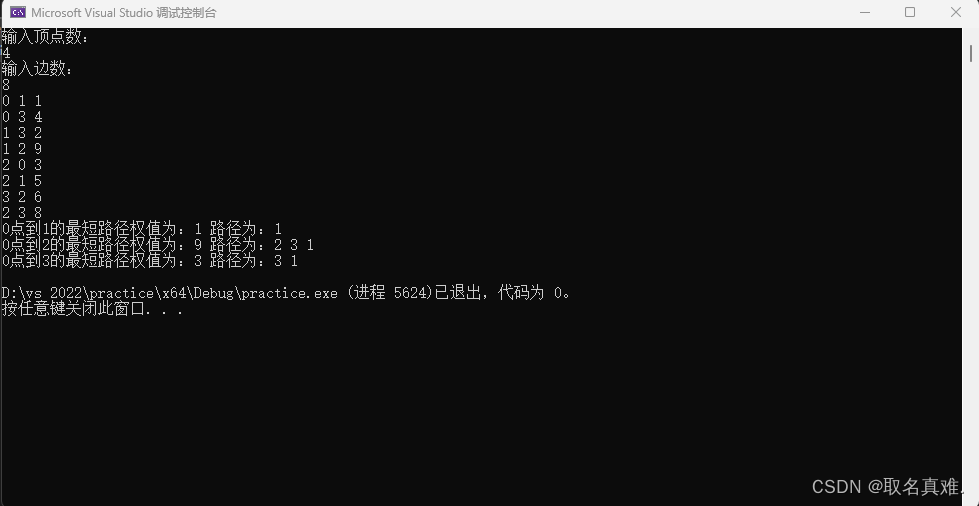
弗洛伊德算法(C++)
目录 介绍: 代码: 结果: 介绍: 弗洛伊德算法(Floyd algorithm)也称为Floyd-Warshall算法,是一种用于求解所有节点对之间的最短路径的动态规划算法。它使用了一个二维数组来存储所有节点…...
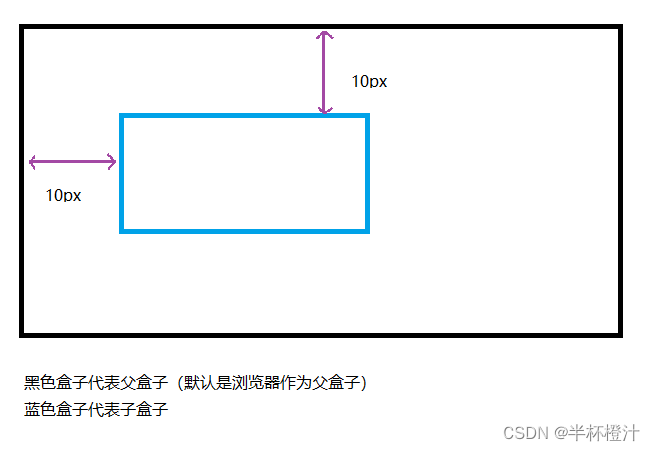
相对定位、绝对定位、固定定位、绝对定位堆叠顺序
相对定位:相对自己本身进行偏移 CSS语法: position: relative;/*相对自己进行定位*/ top: 10px;/*距离上边*/ left: 10px;/*距离左边*/ 演示图: 绝对定位:默认以浏览器进行定位。如果想依照父盒子定位,需要在父盒子…...

px4+vio实现无人机室内定位
文章主要讲述px4 如何利用vins_fusion里程计数据实现在室内定位功能。 文章基于以下软、硬件展开。 硬件软件机载电脑: Intel NUC系统:Ubuntu 20.04相机: Intel Realsense D435iros:noetic飞控:Pixhawk 2.4.8固件&am…...
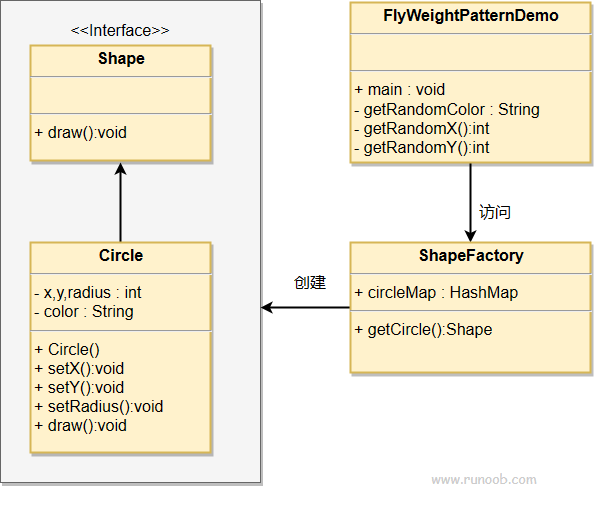
享元模式 rust和java的实现
文章目录 享元模式介绍实现javarust实现代码 rust仓库rust仓库 享元模式 享元模式(Flyweight Pattern)主要用于减少创建对象的数量,以减少内存占用和提高性能。这种类型的设计模式属于结构型模式,它提供了减少对象数量从而改善应…...

XmlElement注解在Java的数组属性上,以产生多个相同的XML元素
例如,下面这段XML数据,有多个data元素,并且它们级别相同: <?xml version"1.0" encoding"UTF-8"?><request><reqtype>05</reqtype><secret>test</secret><body><userid&…...

SQLServer 数字加千分位 用FORMAT函数强转不管多大位数
问题 CONVERT ( money, CONVERT ( money, CAST ( round( FTP_AMOUNT, 2 ) AS NUMERIC ( 20, 2 ) ) ) 1 ) AS FTP_AMOUNT用的money函数 结果空间不足,无法将 money 值转换为 varchar。 可以强转 select FORMAT(CAST ( round( ‘-8926143870680.62000000’, 2 ) AS N…...

说说mvc和mvvm的区别和联系
mvvm 与mvc mvvm 与mvcmvc和mvvm的区别和联系 举例说明mvvm与mvc MVC是一种用于构建应用程序的架构模式,它也将应用程序的逻辑和界面分离。它由三个主要组件组成: 模型(Model):表示应用程序的数据和业务逻辑。视图&a…...
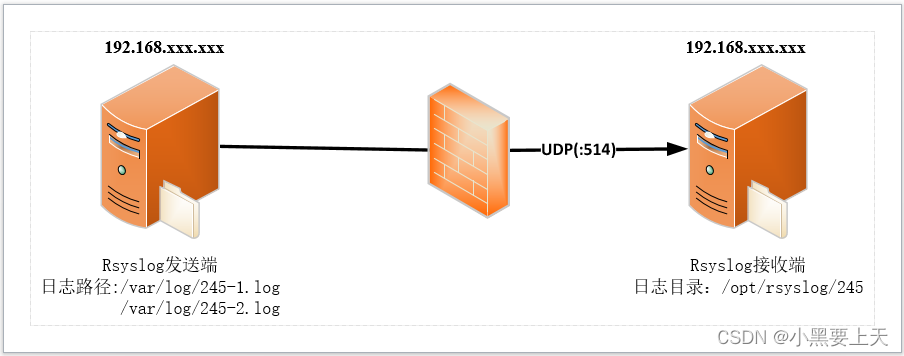
linux rsyslog综合实战2
本次我们通过rsyslog服务将A节点服务器上的两个(E.g:多个日志也可以)日志(Path:/var/log/245-1.log、245-2.log)实时同步到B节点服务器目录下(Path:/opt/rsyslog/245) 1.rsyslog架构 2.环境信息 环境信息 HostnameIpAddressOS versionModuleNotersyslog1192.168.10.245CentOS…...

AcWing 4. 多重背包问题 I 学习笔记
有 N� 种物品和一个容量是 V� 的背包。 第 i� 种物品最多有 si�� 件,每件体积是 vi��,价值是 wi��。 求解将哪些物品装入背包,可使物…...
时,反而打开浏览器的预览界面)
解决selenium使用chrome下载文件(如pdf)时,反而打开浏览器的预览界面
文章目录 解决方法完整的配置 解决方法 在初始化浏览器的时候,添加以下配置即可: option webdriver.ChromeOptions()prefs {"profile.managed_default_content_settings.images": 2, # 禁止加载图片# permissions.default.stylesheet: 2, …...
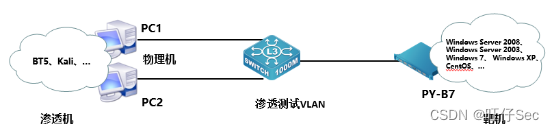
2024年山东省职业院校技能大赛中职组“网络安全”赛项竞赛试题-C
2024年山东省职业院校技能大赛中职组 “网络安全”赛项竞赛试题-C 一、竞赛时间 总计:360分钟 二、竞赛阶段 竞赛阶段 任务阶段 竞赛任务 竞赛时间 分值 A、B模块 A-1 登录安全加固 180分钟 200分 A-2 本地安全策略设置 A-3 流量完整性保护 A-4 …...

基于Python实现用于实时监控和分析 MySQL 服务器的性能指标和相关信息工具源码
MySQL命令行监控工具 - mysqlstat 介绍 mysqlstat 是一个命令行工具,用于实时监控和分析 MySQL 服务器的性能指标和相关信息。 它可以帮助 DBA(数据库管理员)和开发人员定位和解决数据库性能问题。 以下是 mysqlstat 工具的主要功能&#…...

Android 10-13鼠标右键返回功能适配
Android 10-13鼠标右键返回功能适配 文章目录 Android 10-13鼠标右键返回功能适配一、前言二、鼠标右键适配修改1、Android 10 以及更低版本2、Android11 或者更高版本三、总结1、鼠标右键返回功能修改主要代码2、标右键返回修改代码系统源码搜索3、其他 一、前言 Android 原生…...

51单片机/STM32F103/STM32F407学习1_点亮LED灯
目录: 基础知识单片机从0实现单片机GPIO介绍 参考连接: 野火霸天虎教程 https://doc.embedfire.com/products/link/zh/latest/mcu/stm32/ebf_stm32f407_batianhu_v1_v2/download/stm32f407_batianhu_v1_v2.html x.1 基础知识 x.1.1 指针中的取地址&a…...
迁移学习在IMDB上训练情感分析模型)
(Transfer Learning)迁移学习在IMDB上训练情感分析模型
1. 背景 有些场景下,开始的时候数据量很小,如果我们用一个几千条数据训练一个全新的深度机器学习的文本分类模型,效果不会很好。这个时候你有两种选择,1.用传统的机器学习训练,2.利用迁移学习在一个预训练的模型上训练…...
蓝桥杯每日一题2023.11.20
题目描述 “蓝桥杯”练习系统 (lanqiao.cn) 题目分析 方法一:暴力枚举,如果说数字不在正确的位置上也就意味着这个数必须要改变,进行改变记录即可 #include<bits/stdc.h> using namespace std; const int N 2e5 10; int n, a[N], …...

【迅搜02】究竟什么是搜索引擎?正式介绍XunSearch
究竟什么是搜索引擎?正式介绍XunSearch 啥?还要单独讲一下啥是搜索引擎?不就是百度、Google嘛,这玩意天天用,还轮的到你来说? 额,好吧,虽然大家天天都在用,但是我发现&am…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

基于小程序老人监护管理系统源码数据库文档
摘 要 近年来,随着我国人口老龄化问题日益严重,独居和居住养老机构的的老年人数量越来越多。而随着老年人数量的逐步增长,随之而来的是日益突出的老年人问题,尤其是老年人的健康问题,尤其是老年人产生健康问题后&…...
