图论 2023.11.20
次短路
P2829 大逃离
题意:给定一个无向图,入口1,出口n,求第二短路的值
一个节点所直接连接的地方小于k个(起点和终点除外),那么他就不敢进去。
n<=5000,m<=100000
思路:次短路为某一条边的长度+起点到该边一条端点的最短路+终点到另一条边的最短路
spfa跑从起点,从终点的最短路,之后枚举所有的边,连接点的记录可能有重边用vis标记
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
#define fr(i,z,n) for(int i = z;i <= n; i++)
#define fer(i,x) for(int i=e.head[x];i;i=e.next[i])
const int N = 5002, M = 100002, INF = 1e9 + 7;
int n, m, k, mindist, secdist = INF;//mindist最短路,secdist次短路
int t[N], dist[2][N];//t是每个点的出边数
bool used[N], vis[N];
template<size_t size>
struct Road {int to[size], next[size], head[size], cnt = 1;int w[size];void add(int x, int y, int ww) {to[cnt] = y;w[cnt] = ww;next[cnt] = head[x];head[x] = cnt++;}void clear(int n) {for (int i = 0; i <= n; i++) {head[i] = 0;}cnt = 1;}
};
Road<(100010<<1)>e;
void SPFA(int S, int op)//op=0是起点的参数,op=1是终点的参数
{for (int i = 1; i <= n; i++) {dist[op][i] = INF, used[i] = 0;}queue<int> Q;Q.push(S);used[S] = 1;dist[op][S] = 0;while (!Q.empty()){int now = Q.front(); Q.pop();used[now] = 0;fer(i,now){int v = e.to[i];int w = e.w[i];if (dist[op][now] +w < dist[op][v] && t[v] >= k)//筛掉不合法的(即小于k的){dist[op][v] = dist[op][now] + w;if (!used[v]) { Q.push(v); used[v] = 1; }}}}
}
int main() {scanf("%d%d%d", &n, &m, &k);for (int i = 1; i <= m; i++) {int u, v, w;scanf("%d%d%d", &u, &v, &w);e.add(u, v, w);e.add(v, u, w);}fr(i, 1, n) { //记录每一个节点的连接点数memset(vis, 0, sizeof(vis));fer(j, i) {int v = e.to[j];if (!vis[v]) { //防止重边,自环也算t[i]++;vis[v] = 1;}}}t[1] = INF; t[n] = INF; //起点与终点不包括SPFA(1, 0);SPFA(n, 1);mindist = dist[0][n];for (int i = 1; i <= n; i++) { //枚举所有边if (t[i] < k)continue;fer(j, i) {{int v = e.to[j];int len = dist[0][i] + e.w[j] + dist[1][v];if (len > mindist && t[v] >= k)secdist = min(secdist, len);}}}printf("%d\n", secdist >= INF ? -1 : secdist);return 0;
}单源最短路->多源最短路
P5304 [GXOI/GZOI2019] 旅行者(单源最短路->多源最短路)
题意:给定一个有向图,求给定的k个城市的两两城市间最短路的最小值
n<=1e5,m<=5e5,k<=n
思路:两遍dijkstra,
第一次将所有给定点的点加入到队列,(相当于从所有给定点出发到其他点的最短路)
于是需要维护两个东西。1.最短路的距离,2到当前点的最短路的起点(相当于染色操作)
第二次建立反图,同样将所有给定点的点加入到队列,求出其他点到给定点的最短路
同样维护两个东西。1.最短路的距离,2最短路对应的终点
遍历每一条边当起点!=终点(自环)时,更新答案
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#include<array>
#define endl '\n'
#define ios ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO cout<<"NO"<<'\n';
#define fr(i,z,n) for(int i = z;i <= n; i++)
#define fer(i,x) for(int i=e.head[x];i;i=e.next[i])
#define fer1(i,x) for(int i=e1.head[x];i;i=e1.next[i])
#define ufr(i,n,z) for(int i = n;i >= z; i--)
#define int long long
typedef long long ll;
const ll N = 2e5 + 10, inf = 1e18;
const ll mod = 1e9 + 7;
using namespace std;
template<size_t size>
struct Road {int to[size], next[size], head[size], cnt = 1;ll w[size];void add(int x, int y, ll ww) {to[cnt] = y;w[cnt] = ww;next[cnt] = head[x];head[x] = cnt++;}void clear(int n) {for (int i = 0; i <= n; i++) {head[i] = 0;}cnt = 1;}
};
Road<(500010)>e;
Road<(500010)>e1;
int a[N];
int dis1[N], dis2[N];
int col1[N], col2[N];
bool vis[N];
int n, m, k;
void dijkstra1() {fr(i, 1, n) {dis1[i] = inf;vis[i] = 0;}priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > q;fr(i, 1, k) {q.push({ 0,a[i] });dis1[a[i]] = 0;col1[a[i]] = a[i];}while (!q.empty()) {int x = q.top().second;q.pop();if (vis[x]) {continue;}vis[x] = 1;fer(i, x) {int v = e.to[i];int w = e.w[i];if (dis1[x] + w < dis1[v]) {dis1[v] = dis1[x] + w;q.push({ dis1[v],v });col1[v] = col1[x]; //染色,标记起点}}}
}
void dijkstra2() {fr(i, 1, n) {dis2[i] = inf;vis[i] = 0;col2[i] = 0;}priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > q;fr(i, 1, k) {q.push({ 0,a[i] });dis2[a[i]] = 0;col2[a[i]] = a[i];}while (!q.empty()) {int x = q.top().second;q.pop();if (vis[x]) {continue;}vis[x] = 1;fer1(i, x) {int v = e1.to[i];int w = e1.w[i];if (dis2[x] + w < dis2[v]) {dis2[v] = dis2[x] + w;q.push({ dis2[v],v });col2[v] = col2[x]; //染色,标记起点}}}
}
void solve() {cin >> n >> m >> k;e.clear(n);e1.clear(n);vector<array<int, 3>>ve;fr(i, 1, n) {col1[i] = 0;col2[i] = 0;}fr(i, 1, m) {int u, v, w;cin >> u >> v >> w;e.add(u, v, w); //有向图e1.add(v, u, w);ve.push_back({ u,v,w });}fr(i, 1, k) {cin >> a[i];}dijkstra1();dijkstra2();int ans = inf;for (auto it : ve) { //遍历所有的边int u = it[0];int v = it[1];int w = it[2];// cout << u << ' ' << v << ' ' << col1[u] << ' ' << col2[v] << '\n';if ((col1[u]&&col2[v]) && col1[u] != col2[v]) {// cout << "YES" << '\n';ans = min(ans, dis1[u] + dis2[v]+w);}}cout << ans << '\n';
}signed main()
{ios;int t = 1;cin >> t;while (t--) {solve();}
}
割点+联通块
P3469 [POI2008] BLO-Blockade
给定一个无向图(图是联通的),无重边,对于每个节点求出去与节点i关联的所有边去掉以后(不去掉节点i本身),
无向图有多少个有序点(x, y),满足x 和y 不连通。
n<=1e5,m<=5e5
讨论要删的点是不是割点:
1.非割点,则为2*(n-1)
2.割点,导致变成多个联通块,不同联通块不可相互到达,
假设割后产生2个的联通块,大小为a,b,则贡献为2ab+2(n-1),
假设产生k联通块2(n-1)+2∑(1<=i<=k)∑(1<=j<=k,j!=i)sizei*sizej
会超时,∑(1<=j<=k,j!=i)sizej优化为n-sizei-1
于是变为2∑(1<=i<=k)sizei*(n-sizei-1)
转为求联通块大小问题
再dfs的过程中用sum防止重复计算的
#include<iostream>
#include<stack>
#include<algorithm>
#include<vector>
#include<queue>
#define int long long
const int N = 5e5 + 10;
using namespace std;
vector<int> edges[N];
vector<int> edges2[N];
stack<int>stk;
int dfsn[N], low[N], instk[N], cnt;
int n, m;
int ans[N], Size[N];
int tot;
void tarjan(int p){low[p] = dfsn[p] = ++cnt;instk[p] = 1;Size[p] = 1; int sum = 0;stk.push(p); // 进栈for (auto q : edges[p]) {if (!dfsn[q]) { // 未访问过tarjan(q); // 递归地搜索Size[p] += Size[q]; //子树的大小 if (low[q] >= dfsn[p]) { // p为割点满足low[q] >= dfsn[p]ans[p] += Size[q] *(sum); //以p为子树的贡献点sum += Size[q];} low[p] = min(low[p], low[q]);}else {low[p] = min(low[p], dfsn[q]);}}ans[p] += (n - sum - 1) * sum;//剩下的点产生的贡献!ans[p] += n - 1;
}
signed main() {cin >> n >> m;for (int i = 1; i <= m; i++) {int x, y;cin >> x >> y;edges[x].push_back(y);edges[y].push_back(x);}for (int i = 1; i <= n; ++i)if (!dfsn[i])tarjan(i);for (int i = 1; i <= n; i++) {cout << 2*ans[i] << '\n';}
}
相关文章:

图论 2023.11.20
次短路 P2829 大逃离 题意:给定一个无向图,入口1,出口n,求第二短路的值 一个节点所直接连接的地方小于k个(起点和终点除外),那么他就不敢进去。 n<5000,m<100000 思路:次短路…...
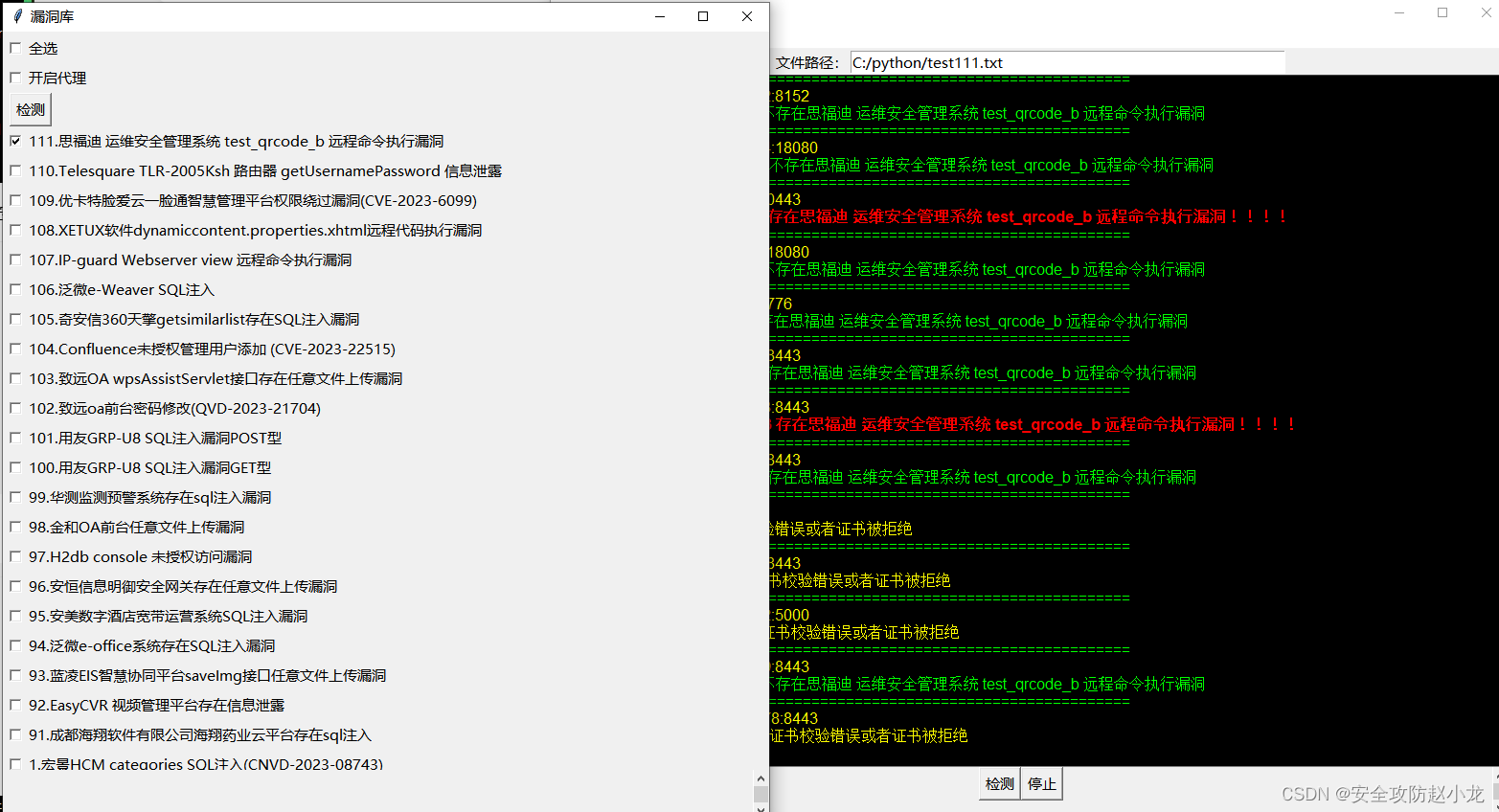
思福迪 运维安全管理系统 test_qrcode_b 远程命令执行漏洞
思福迪 运维安全管理系统 test_qrcode_b 远程命令执行漏洞 一、漏洞描述二、漏洞影响三、网络测绘四、漏洞复现1.手动复现2.自动化复现3.python源代码 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任…...

electron项目开机自启动
一、效果展示:界面控制是否需要开机自启动 二、代码实现: 1、在渲染进程login.html中,画好界面,默认勾选; <div class"intro">开机自启动 <input type"checkbox" id"checkbox&quo…...

2023年约特干故城夜间演艺《万方乐奏有于阗》完美谢幕
11月19日,记者走进约特干故城看到演员在欢乐地跳着刀郎舞和古典舞,庆祝今年以来夜间演艺《万方乐奏有于阗》演出200场完美谢幕。 11月19日在约特干故城,演员正在表演迎宾乐舞。阿卜力克木依卜拉依木摄 当天晚上,城楼上旌旗猎猎&am…...
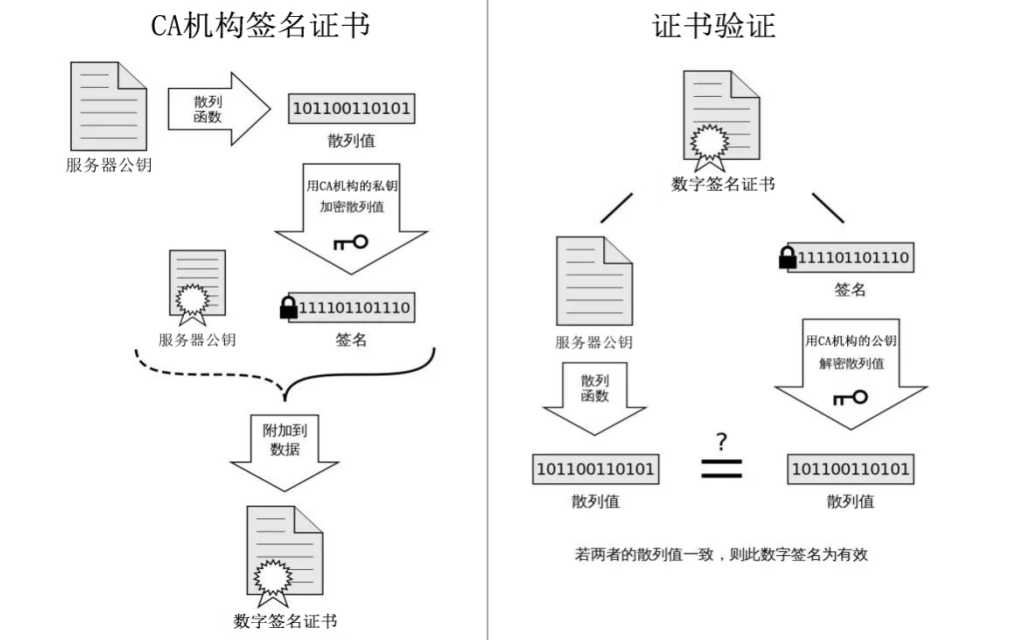
学习网络编程No.10【深入学习HTTPS】
引言: 北京时间:2023/11/14/18:45,因为种种原因,上个月的文章昨天才更新,目前处于刷题前夕,算法课在看了。这次和以前不一样,因为以前对知识框架没有很好的理念,并不清楚相关知识要…...
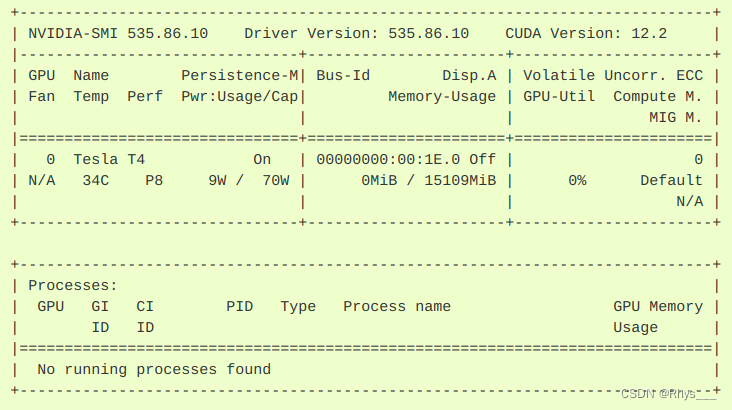
ubuntu下docker环境使用GPU配置
本文主要讲述整个命令流程,具体讲解请看官网nvidia-容器工具包和一篇总结得很详细的博文docker使用GPU总结 docker的版本必须安装19.0版本以上的,这里也只讲19.0版本以上的使用方法 首先设置一下网络信息 curl -fsSL https://nvidia.github.io/libnvi…...

渗透工具---BurpSuite 插件开发之HelloWorld
本文主要记录如何利用burp官方的新版API即MontoyaApi 写helloworld(上一篇的demo使用旧版api写的,这篇及后续开发将采用新版api) 先看效果图 更多详细内容见下方 这里有更详细更全面的代码内容 以及配置相关的内容 https://mp.weixin.qq.co…...

2216. 美化数组的最少删除数
我的做法: 使用一个index作为检查坐标,当index为偶数时检查当前数和后一个数是否相等,相等的话,后一个数设置为-1,注意如果相等,要把相等的数保留下来last,以便接下来检查,防止出现2…...

竞赛 题目:基于深度学习的人脸表情识别 - 卷积神经网络 竞赛项目 代码
文章目录 0 简介1 项目说明2 数据集介绍:3 思路分析及代码实现3.1 数据可视化3.2 数据分离3.3 数据可视化3.4 在pytorch下创建数据集3.4.1 创建data-label对照表3.4.2 重写Dataset类3.4.3 数据集的使用 4 网络模型搭建4.1 训练模型4.2 模型的保存与加载 5 相关源码6…...

基于安卓android微信小程序的好物分享系统
运行环境 开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包&a…...
【Spring Boot】使用WebSocket协议完成来单提醒及客户催单功能
1 WebSocket介绍 WebSocket 是基于 TCP 的一种新的网络协议。它实现了浏览器与服务器全双工通信(双向传输)——浏览器和服务器只需要完成一次握手,两者之间就可以创建持久性的连接, 并进行双向数据传输。 1.1 HTTP协议和WebSocket协议对比 1、HTTP是短…...

如何有效的禁止Google Chrome自动更新?
禁止Chrome自动更新 1、背景2、操作步骤 1、背景 众所周知,当我们在使用Selenium进行Web自动化操作(如爬虫)时,一般会用到ChromeDriver。然而Driver的更新速度明显跟不上Chrome的自动更新。导致我们在使用Selenium进行一些操作时就…...

OpenShift 4 - 部署 RHODS 环境,运行 AI/ML 应用(视频)
《OpenShift / RHEL / DevSecOps 汇总目录》 说明:本文已经在 OpenShift 4.14 RHODS 1.33 的环境中验证 文章目录 RHODS 简介安装 RHODS 环境运行环境说明用 RHODS Operator 安装环境创建 Jupyter Notebook 运行环境 开发调式 AI/ML 应用部署运行 AI/ML 应用视频参…...

MySQL 的执行原理(二)
5.3. MySQL 的查询成本 5.3. MySQL 的查询成本 MySQL 执行一个查询可以有不同的执行方案,它会选择其中成本最低,或者 说代价最低的那种方案去真正的执行查询。不过我们之前对成本的描述是非常模 糊的,其实在 MySQL 中一条查询语句的执行成本…...
 和 =any(?) 用法/性能对比)
postgres in (?,?) 和 =any(?) 用法/性能对比
刚刚回顾了一下 JDBC 操作 SQL Server 时如何传入列表参数,即如何给 in (?) 条件直接传入一个列表参数,然而本质上是不支持,最终不得不展开为 in (?, ?,...?) 针对每个元素单独设置参数,不定长的参数对于重用已编译 PreparedS…...

46. Qt Android调用Java代码进行辅助开发 -- 框架搭建
1. 说明 使用Qt进行android开发时,某种情况下使用C++的知识或者Qt提供的方法是无法满足功能需求的,即使通过各种手段能够勉强实现功能,也非常的麻烦。此时,就需要Java来辅助实现了。在Qt中提供了调用Java代码的接口,比较方便。本片博客先介绍如何搭建一个能够调用java代码…...

NX二次开发UF_CAM_PREF_set_logical_value 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CAM_PREF_set_logical_value Defined in: uf_cam_prefs.h int UF_CAM_PREF_set_logical_value(UF_CAM_PREF_t pref, logical value ) overview 概述 This function sets the lo…...

docker下移除不使用的镜像、容器、卷、网络
Prune images docker image prune移除没有标签并且没有被容器引用的镜像,这种镜像称为 dangling(摇晃的) 镜像。 示例1:docker image prune 删除了redis,无标签且无引用 docker ps -a CONTAINER ID IMAGE COMMAND CREATED STA…...
C语言基本算法之选择排序
目录 概要: 代码如下 运行结果如下 概要: 它和冒泡排序一样,都是把数组元素按顺序排列,但是方法不同,冒泡排序是把较小值一个一个往后面移,选择排序则是直接找出最小值,可以这个说ÿ…...
服务器数据恢复—raid5上层NTFS分区误删除/格式化的数据恢复案例
NTFS是windows操作系统服务器应用最为广泛的文件系统之一。理论上,NTFS文件系统格式化操作虽然不会对数据造成太大的影响,但是有可能会出现部分文件目录结构丢失的情况。下面介绍一台服务器误操作导致raid5阵列上层的NTFS分区被格式化后如何逆向操作恢复…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
