算法设计与分析复习--分支界限法
文章目录
- 上一篇
- 分支界限法性质
- 装载问题
- 0-1背包问题
- 单源最短路问题
- 最大团问题
- 下一篇
上一篇
算法设计与分析复习–回溯法(二)
分支界限法性质
分支界限法是按广度优先策略或最小耗费优先遍历问题的解空间树。
搜索解空间:
- 子集树
- 排列树
搜索方式:广度优先遍历(队列)或最小耗费优先(堆)
方法:确定解空间,设计合适的限界函数(在拓展时删除不必要的孩子结点),组织活结点表
但是由于每一层对应的cw, rw是不同的,所以需要用一个node的数据结构存储每一个节点的
装载问题
问题描述:n个集装箱要装到2艘重量分别 c 1 c_1 c1, c 2 c_2 c2的货轮,其中集装箱 i i i的重量为 w i w_i wi器满足集装箱重量之和小于两轮船载重。
最优装载方案:将第一艘船尽可能装满,将剩余的货箱装到第二搜轮船上。
约束函数:所装货物重量小于第一艘船载重
上界函数是:已装重量+剩余重量上界
使用队列的方式
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>using namespace std;const int N = 110;int a[N], n, c1, sum = 0, bw = 0;struct node
{int idx; // 层数int cw; // 当前层的重量int rw; // 剩余的重量
};void bfs()
{queue<node> q;q.push({0, 0, sum});while (q.size()){auto t = q.front();q.pop();bw = max(bw, t.cw); // 更新最大重量// 左扩展if (t.idx < n && t.cw + a[t.idx] <= c1){q.push({t.idx + 1, t.cw + a[t.idx], t.rw - a[t.idx]});}// 右扩展if (t.idx < n && t.cw + t.rw > bw){q.push({t.idx + 1, t.cw, t.rw - a[t.idx]});}}
}int main()
{scanf("%d%d", &n, &c1);for (int i = 0; i < n; i++){scanf("%d", &a[i]);sum += a[i];}bfs();printf("%d\n", bw);return 0;
}
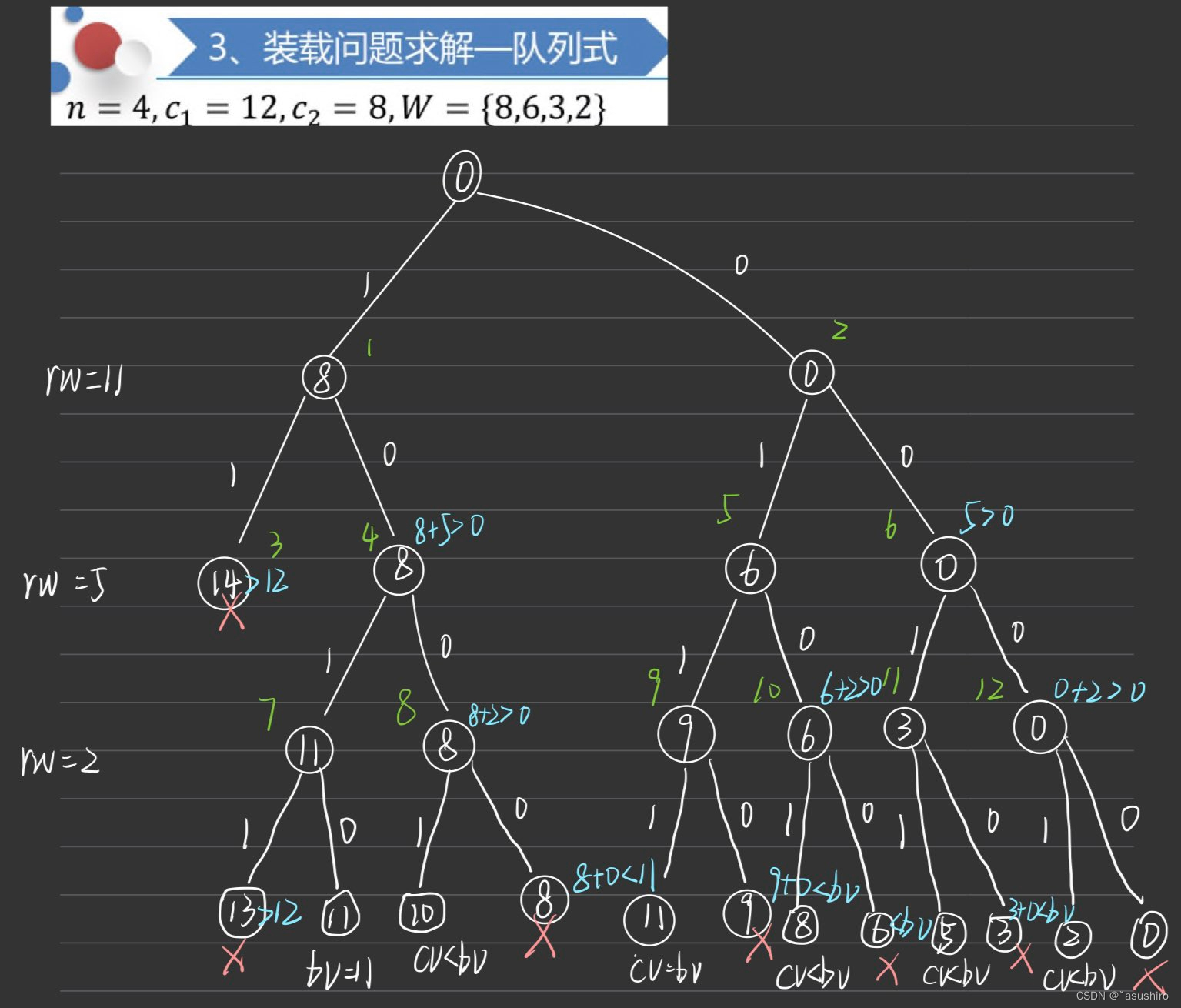
利用优先级进行查找时
我们将利用当前结点的价值上界
c w + r w cw + rw cw+rw
进行堆的构造
重构堆需要
priority_queue<node, vector<node>, cmp> heap;
cmp为比较函数,不过要比较符相反

例如greater是返回更大的
而构造小根堆就用greater
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>using namespace std;const int N = 110;int a[N], n, c1, sum = 0, bw = 0;struct node
{int idx; // 层数int cw; // 当前层的重量int rw; // 剩余的重量
};struct cmp
{bool operator ()(const node &x, const node &y) const{return (x.cw + x.cw) < (y.cw + y.rw); // 优先队列的优先级按当前上界要用更大排,这里就要是小于}
};void bfs()
{priority_queue<node, vector<node>, cmp > heap;heap.push({0, 0, sum});while (!heap.empty()){auto t = heap.top();heap.pop();bw = max(bw, t.cw); // 更新最大重量// 左扩展if (t.idx < n && t.cw + a[t.idx] <= c1){heap.push({t.idx + 1, t.cw + a[t.idx], t.rw - a[t.idx]});}// 右扩展if (t.idx < n && t.cw + t.rw > bw){heap.push({t.idx + 1, t.cw, t.rw - a[t.idx]});}}
}int main()
{scanf("%d%d", &n, &c1);for (int i = 0; i < n; i++){scanf("%d", &a[i]);sum += a[i];}bfs();printf("%d\n", bw);return 0;
}
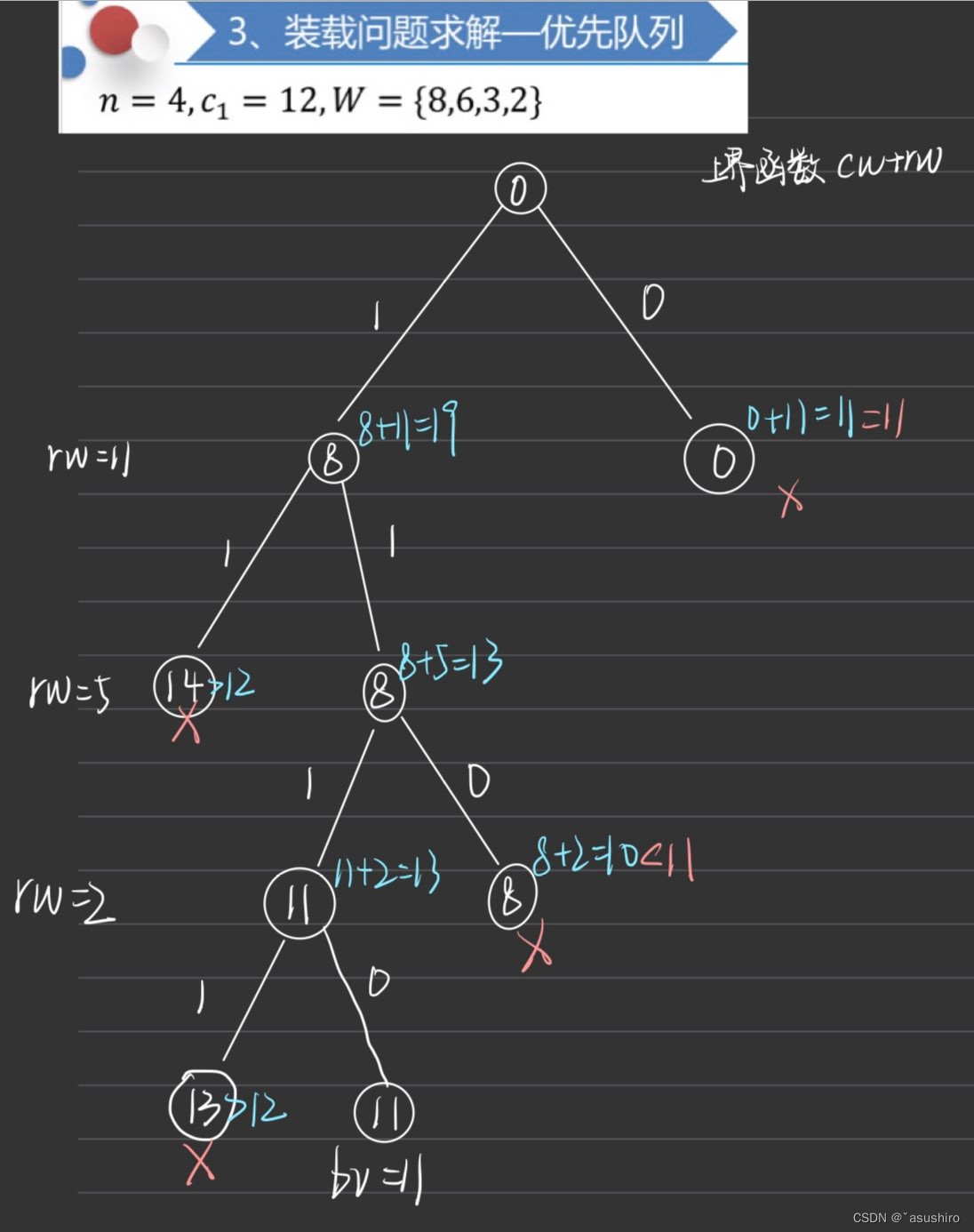
由于优先队列的方式更难一些所以后面实现都是优先队列的方式
0-1背包问题
求法与装载问题一样,不如说装载问题特化成了0-1背包问题
但是在右剪枝的求法上和回溯法一样
但是bound函数用法不同了,bound就是求上界的函数,并且求得是当前结点的上界
左剪枝:不超过背包容量
右剪枝:cv + rv >= bv
rv是利用贪心背包的方式求得的
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>using namespace std;
typedef pair<double, double> PDD;const int N = 110;int n, c;
vector<PDD> ob;
double bv = 0, sv = 0; // 将bv, sv初始化为0struct node
{int idx;double cw;double cv;double ub;bool operator< (const node &x) const{return ub < x.ub;//利用ub堆排序}
};bool cmp(PDD x, PDD y)
{return (x.second / x.first) > (y.second / y.first);//贪心排序
}double bound(node x)
{double rcv = x.cv, rw = c - x.cw;int i = x.idx;//不同于回溯法,在输入时改变i的值,因为要计算当前结点的上界while (i < n && ob[i].first <= rw){rw -= ob[i].first;rcv += ob[i].second;i++;}if (i < n)rcv += rw * (ob[i].second / ob[i].first);return rcv;
}void bfs()
{priority_queue<node> heap;heap.push({0, 0, 0, bound({0, 0, 0, 0})}); // 初始节点的上界需要计算while (heap.size()){auto t = heap.top();heap.pop();printf("{%d, %d, %.1lf}\n", (int)t.cw, (int)t.cv, t.ub);//搜索顺序可视化if (t.idx == n)//到达叶子结点{if (t.cv > bv){bv = t.cv;}continue; }if (t.cw + ob[t.idx].first <= c) // 向左走heap.push({t.idx + 1, t.cw + ob[t.idx].first, t.cv + ob[t.idx].second, t.ub}); node tmp = {t.idx + 1, t.cw, t.cv, bound({t.idx + 1, t.cw, t.cv, 0})};//需要填两次,定义临时变量if (bound(tmp) > bv)heap.push(tmp); // 向右走}
}int main()
{scanf("%d%d", &n, &c);for (int i = 0; i < n; i++){double w, v;scanf("%lf%lf", &w, &v);sv += v;ob.push_back({w, v});}sort(ob.begin(), ob.end(), cmp);bfs();printf("%d\n", (int)bv);return 0;
}
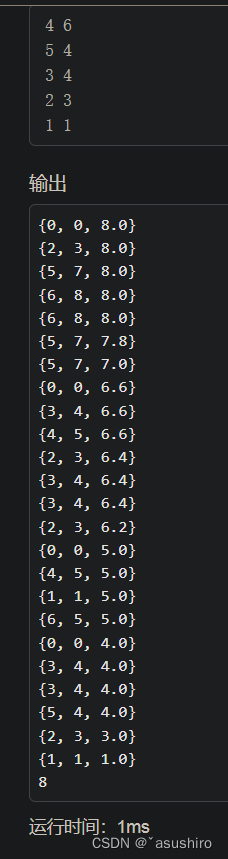

单源最短路问题
问题描述:给定一个带权有向图G = (V, E), 每条边的权值是一个正整数, 给定V中的一个顶点S,称作源点。要求:计算从源点到其他所有顶点的最短路径长度。
AcWing 850. Dijkstra求最短路 II
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>using namespace std;typedef pair<int, int> PII;const int N = 1e6 + 10;int h[N], e[N], w[N], ne[N], idx = 0;
int dist[N], pre[N];
vector<int> ans;
bool st[N];
int n, m;void add (int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}void traceback(int k)
{if (k == 0) return;ans.push_back(k);traceback(pre[k]);
}int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, 1});// first表示距离, second表示节点编号,这是因为在优先队列中是优先按元祖第一个元素进行排序while (heap.size()){auto t = heap.top();heap.pop();int ver = t.second, distance = t.first;// ver表示节点编号if (st[ver])continue;st[ver] = true;for (int i = h[ver]; ~i; i = ne[i]){int j = e[i];if (dist[j] > distance + w[i])// 因为要遍历Ver相连的所有边i所以提前将源点到ver的最短距离记作distance, 而w[i]记录的是第i个节点到j的距离(权重)i是与ver相连的边 // 将与ver相连的边更新为最短路径值,j是i的下一条边是一个指针关系{dist[j] = distance + w[i];pre[j] = ver;heap.push({dist[j], j});}}}if (dist[n] == 0x3f3f3f3f) return -1;else {traceback(n);reverse(ans.begin(), ans.end());puts("最短路径为:");for (auto i : ans)printf("%d ", i);puts("");return dist[n];}
}int main ()
{cin >> n >> m;memset(h, -1, sizeof h);for (int i = 0; i < m; i ++){int a, b, c;scanf("%d%d%d", &a, &b, &c);add (a, b, c);}printf("路径长度为:%d", dijkstra());return 0;
}

最大团问题
问题描述:给定无向图G = (V, E)。如果 U ⊆ V U\subseteq V U⊆V, 求对任意 u , v ∈ U u, v \in U u,v∈U有 ( u , v ) ∈ E (u, v) \in E (u,v)∈E, 则称U是G的完全子图。
最大团就是一个图含顶点数最大的完全图,且要是这个图的子集。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>using namespace std;const int N = 110;int g[N][N], n, m, bn;
vector<int> ans;struct node
{int idx;int cn;vector<int> x;int un;bool operator< (const node &p) const{return un < p.un;}
};bool constrain(node c)
{for (int i = 0; i < c.idx - 1; i ++)//这里i不能到c.idx不然就会有它自身到自身为0会返回false,{if (c.x[i] == 1 && g[c.idx][i + 1] == 0)//x的下标是从0开始,而g[i][j]的下标是从1开始,所以要进行调整return false;}return true;
}void bfs()
{priority_queue<node> heap;heap.push({0, 0, {}, n});while (heap.size()){auto t = heap.top();heap.pop();if (t.idx == n){if (t.cn > bn){ans = t.x;bn = t.cn;}continue;}node tmp = {t.idx + 1, t.cn + 1, t.x, t.un};tmp.x.push_back(1);//要提前加入,否则判断是少条件if (constrain(tmp))heap.push(tmp);tmp = {t.idx + 1, t.cn, t.x, t.un - 1};tmp.x.push_back(0);if (tmp.un >= bn)heap.push(tmp);}
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < m; i ++){int a, b;scanf("%d%d", &a, &b);g[a][b] = g[b][a] = 1;}bfs();printf("%d\n", bn);for (auto val : ans) {printf("%d ", val);}return 0;
}
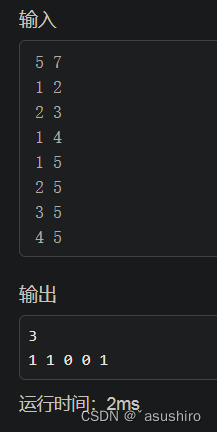

下一篇
未完待续
相关文章:

算法设计与分析复习--分支界限法
文章目录 上一篇分支界限法性质装载问题0-1背包问题单源最短路问题最大团问题下一篇 上一篇 算法设计与分析复习–回溯法(二) 分支界限法性质 分支界限法是按广度优先策略或最小耗费优先遍历问题的解空间树。 搜索解空间: 子集树排列树 …...

Https攻击怎么防御
随着互联网技术的发展,网站所遭受的网络攻击频率也在不断上升。某种程度上,我们可以说互联网上的每个网站都容易遭受安全攻击。因为网络攻击者最主要的动机是求财。无论你运营的是电子商务项目还是简单的小型商业网站,潜在攻击的风险就在那里…...
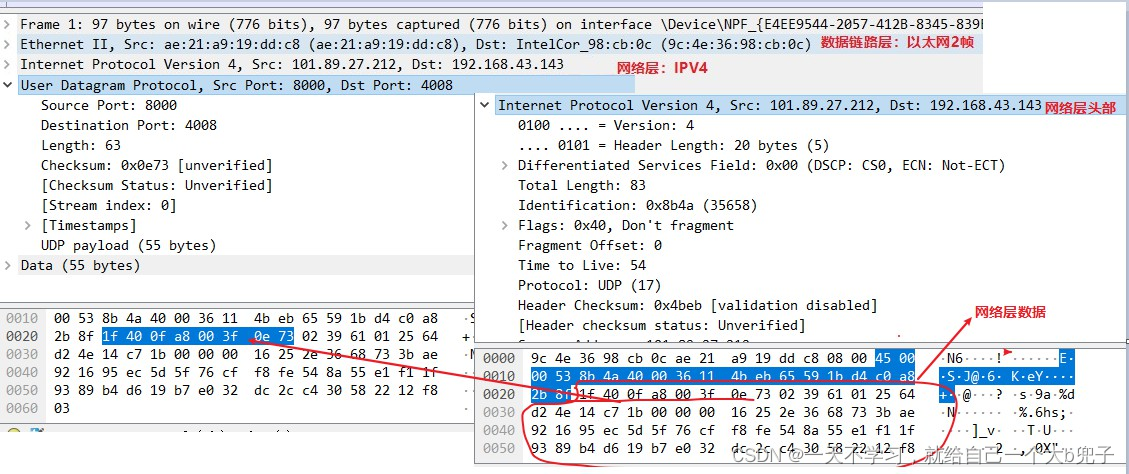
网络知识学习(笔记二)
ios模型规定的网络模型一共有7层,但是实际使用过程中,4层的TCP/IP模型是经常使用的,网络知识学习笔记里面也是基于4层TCP/IP模型进行分析的,前面已经讲了:(1)物理层,(2&a…...
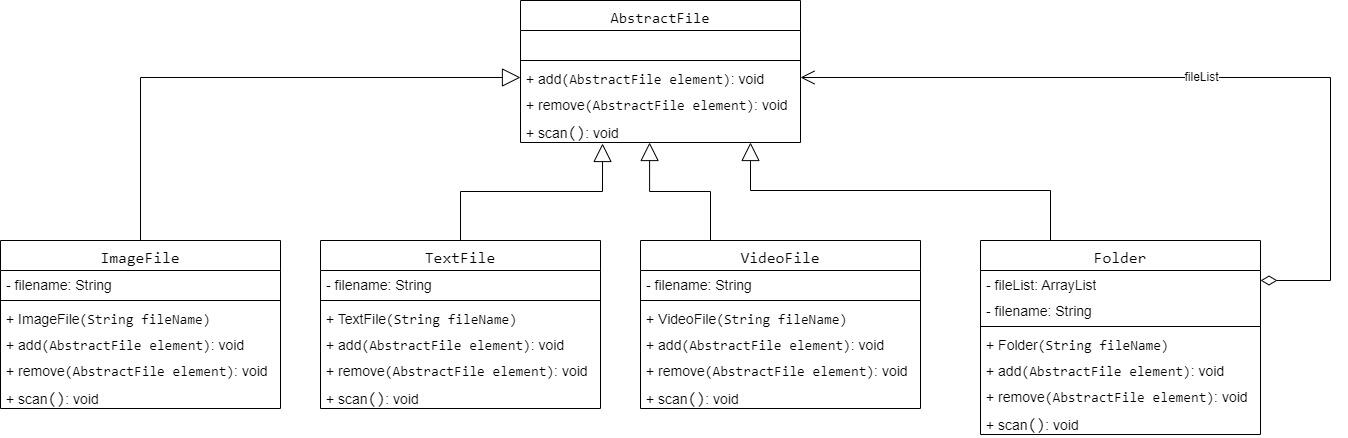
万字解析设计模式之组合模式、亨元模式
一、组合模式 1.1概述 组合模式是一种结构型设计模式,它允许将对象组合成树形结构,以表示“部分-整体”的层次结构。组合模式使得客户端可以一致地对待单个对象和对象组合,从而将复杂的层次结构展现为一个统一的树形结构。 在组合模式中&…...

HTTP之常见问答
1:HTTP/1.1 如何优化? :尽量避免发送 HTTP 请求;通过缓存技术,使用请求的 Etag 参数来处理判断缓存过期等问题,类似304状态码就是告诉客户端,缓存有效还能继续使用 :在需要发送 HTTP…...

java伪共享问题
参考文章 https://blog.csdn.net/qq_45443475/article/details/131417090 产生原因 cpu 与内核数据交换的单位是 cache 行,多核 cpu 的高速缓存在对同一个变量进行修改时由于缓存一致性协议导致对应的缓存失效。 缓存行的大小 cpu 架构有关系,如果是 …...
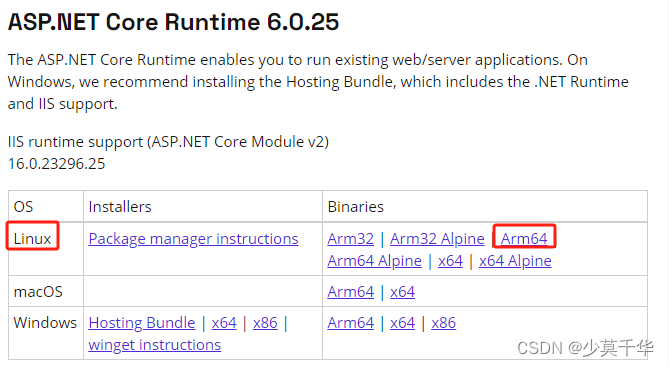
【Ubuntu】Ubuntu arm64 部署 Blazor Server 应用
部署步骤 发布安装运行环境:dotnet-sdk(必装)、aspnetcore-runtime、dotnet-runtime安装证书设置环境变量:临时变量、当前用户永久变量、所有用户的永久变量运行:终端运行、后台运行 基本情况 开发系统环境 系统&am…...
Android加固为何重要?很多人不学
为什么要加固? APP加固是对APP代码逻辑的一种保护。原理是将应用文件进行某种形式的转换,包括不限于隐藏,混淆,加密等操作,进一步保护软件的利益不受损坏。总结主要有以下三方面预期效果: 1.防篡改&#x…...

【C/PTA】函数专项练习(一)
本文结合PTA专项练习带领读者掌握函数,刷题为主注释为辅,在代码中理解思路,其它不做过多叙述。 目录 6-1 输出星期名6-2 三整数最大值6-3 数据排序6-4 多项式求值 6-1 输出星期名 请编写函数,根据星期数输出对应的星期名。 函数原…...

SUDS: Scalable Urban Dynamic Scenes
SUDS: Scalable Urban Dynamic Scenes:可扩展的城市动态场景 创新点 1.将场景分解为三个单独的哈希表数据结构,以高效地编码静态、动态和远场辐射场 2.利用无标签的目标信号,包括RGB图像、稀疏LiDAR、现成的自监督2D描述符,以及…...

蓝桥杯算法双周赛心得——迷宫逃脱(记忆化搜索)
大家好,我是晴天学长,非常经典实用的记忆化搜索题,当然也可以用dp做,我也会发dp的题解,需要的小伙伴可以关注支持一下哦!后续会继续更新的。💪💪💪 1) .迷宫逃脱 迷官逃脱…...
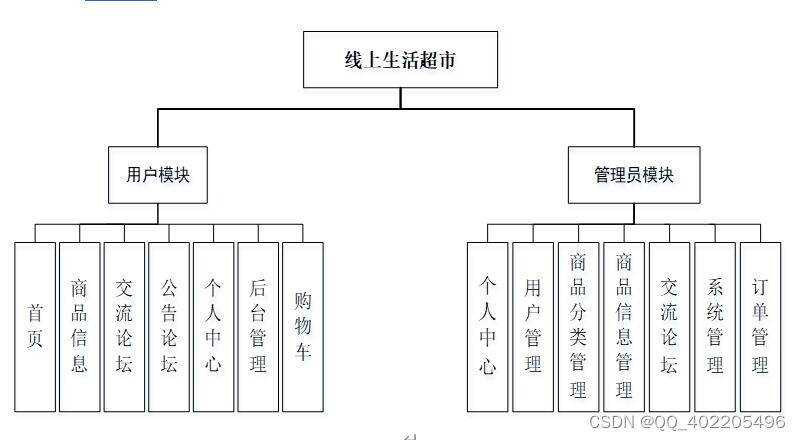
nodejs+vue线上生活超市购物商城系统w2c42
超市管理系统的开发流程包括对超市管理系统的需求分析,软件的设计建模以及编写程序实现系统所需功能这三个阶段。对超市管理系统的需求分析。在这个阶段,通过查阅书籍,走访商场搜集相关资料,了解经营者对软件功能的具体所需和建议…...
飞翔的小鸟
运行游戏如下: 碰到柱子就结束游戏 App GameApp类 package App;import main.GameFrame;public class GameApp {public static void main(String[] args) {//游戏的入口new GameFrame();} } main Barrier 类 package main;import util.Constant; import util.Ga…...

浅析OKR的敏捷性
前言 OKR对于工作的提升有着一定的不可替代的作用。特别在敏捷方面。 OKR的敏捷性 OKR(Objectives and Key Results)是一种目标设定框架,它的敏捷性主要体现在以下几个方面: 公开透明 OKR要求完全公开透明,让每个员…...
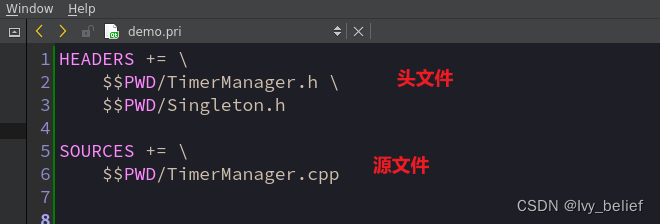
Linux+qt:创建动态库so,以及如何使用(详细步骤)
目录 1、根据安装Qt Creator的向导进行创建 2、开发动态库注意的一些细节 3、给动态库添加一个对外开放的接口文件 4、了解下Qt的 .pri文件(非常实用) 5、如何调用动态库.so 1、根据安装Qt Creator的向导进行创建 (1)选择“…...

如何将Docker的构建时间减少40%
与许多公司类似,我们为产品中使用的所有组件构建docker映像。随着时间的推移,其中一些映像变得越来越大,我们的CI构建花费的时间也越来越长。我的目标是CI构建不超过5分钟——差不多是喝杯咖啡休息的理想时间。如果构建花费的时间超过这个时间…...
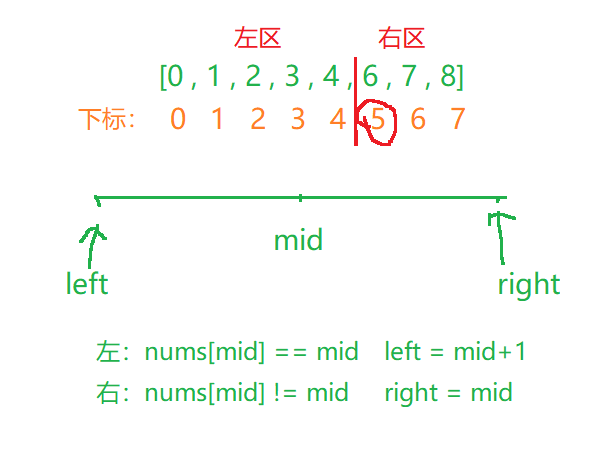
二分查找——经典题目合集
文章目录 🦜69. x 的平方根🌼题目🌻算法原理🌷代码实现 🐳35. 搜索插入位置🌼题目🌻算法原理🌷代码实现 🦭852. 山脉数组的峰顶索引🌼题目🌻算法原…...

在Jupyter Lab中使用多个环境,及魔法命令简介
一、Jupyter Lab使用conda虚拟环境 1、给虚拟环境添加 ipykernel 方法一: 创建环境时直接添加ipykernel 方法:conda create -n 【虚拟环境名称】python3.8 ipykernel实例如下: conda create -n tensorflow_cpu python3.8 ipykernel 方法二ÿ…...
知虾数据软件:电商人必备知虾数据软件,轻松掌握市场趋势
在当今数字化时代,数据已经成为了企业决策的重要依据。对于电商行业来说,数据更是至关重要。如果你想在电商领域中脱颖而出,那么你需要一款强大的数据分析工具来帮助你更好地了解市场、分析竞争对手、优化运营策略。而知虾数据软件就是这样一…...

c语言中*p1++和p1++有啥区别
在C语言中,*p1和p1是两个不同的表达式,有以下区别: *p1:这是一个后缀递增运算符的组合。首先,*p1会取出指针p1所指向的值,并且对p1进行递增操作。简而言之,这个表达式会先取出p1指向的值&#x…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
