力扣算法练习BM45—滑块窗口的最大值
题目
给定一个长度为 n 的数组 num 和滑动窗口的大小 size ,找出所有滑动窗口里数值的最大值。
例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
窗口大于数组长度或窗口长度为0的时候,返回空。
数据范围: 1≤n≤10000,0≤size≤10000,数组中每个元素的值满足 ∣val∣≤10000
要求:空间复杂度 O(n),时间复杂度)O(n)
示例1
输入:[2,3,4,2,6,2,5,1],3
返回值:[4,4,6,6,6,5]
解题思路
1.如果滑动窗口的大小为0,则直接返回空列表
2.不为0,则依次以滑动窗口的大小作为每次遍历的长度,每次滑动向后移动一位,依次遍历查找每个窗口中的最大值
题解
#
# 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
#
#
# @param num int整型一维数组
# @param size int整型
# @return int整型一维数组
#
class Solution:def maxInWindows(self , num: List[int], size: int) -> List[int]:# 1.如果滑动窗口的大小为0,则直接返回空列表if size==0: return[]# 2.不为0,则依次以滑动窗口的大小作为每次遍历的长度,每次滑动向后移动一位,依次遍历查找每个窗口中的最大值max_list =[]n=0l=len(num)while n+size<=l:max=num[n]for i in range(n,n+size):print(num[i])if max<num[i]:max=num[i]max_list.append(max)n+=1return max_list相关文章:

力扣算法练习BM45—滑块窗口的最大值
题目 给定一个长度为 n 的数组 num 和滑动窗口的大小 size ,找出所有滑动窗口里数值的最大值。 例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针…...

最小二乘估计及与极大似然估计的关系
最小二乘估计(Least Squares Estimation)和极大似然估计(Maximum Likelihood Estimation)是统计学中常用的参数估计方法,它们在某些情况下是等价的,但在一般情况下并不总是相同的。 最小二乘估计ÿ…...
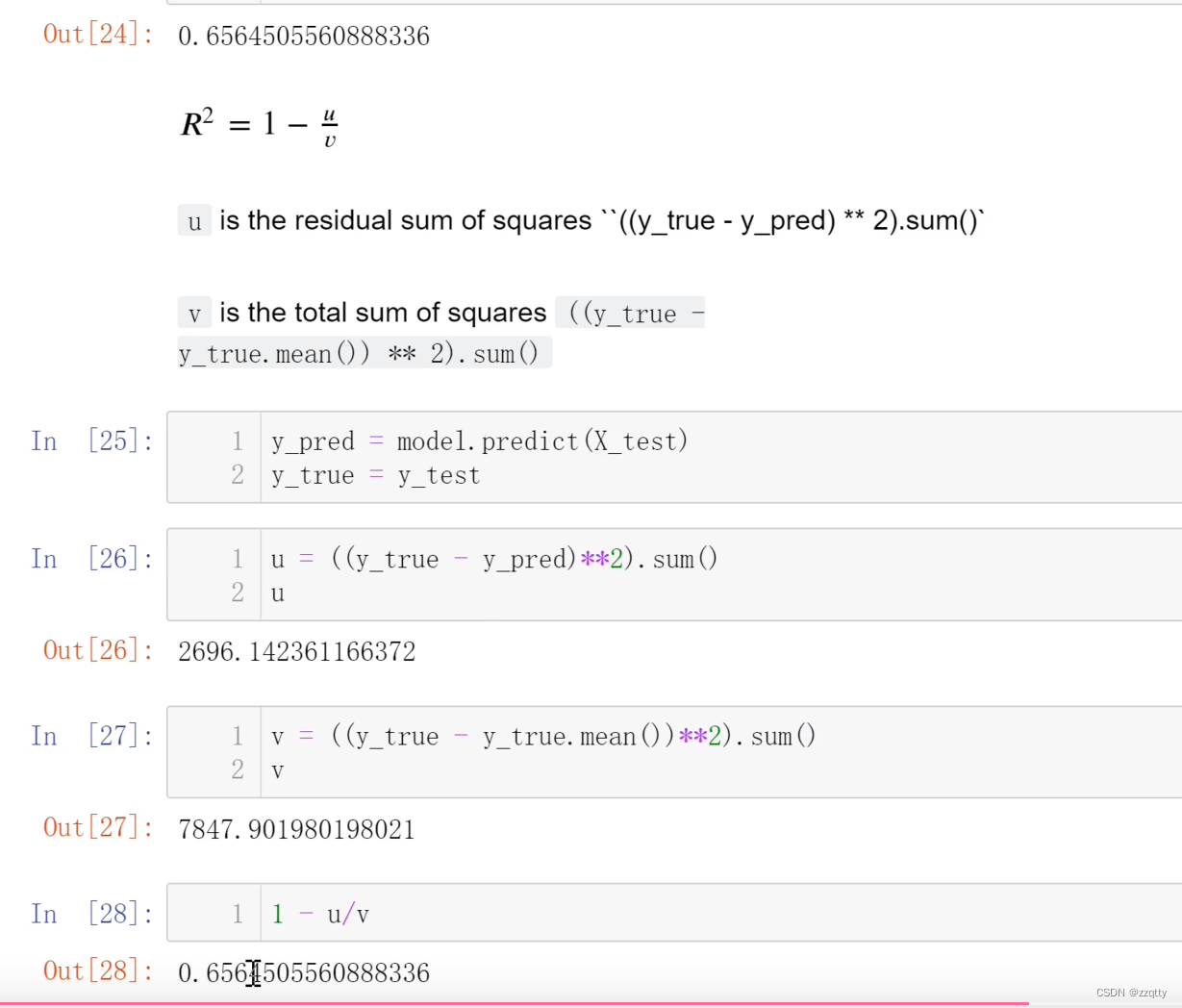
02房价预测
目录 代码 评分算法: 代码 import numpy as np from sklearn import datasets from sklearn.linear_model import LinearRegression# 指定版本才有数据集 # C:\Users\14817\PycharmProjects\pythonProject1\venv\Scripts\activate.bat # pip install scikit-le…...

【Springboot】pom.xml中的<build>标签详解
默认值及其标签解释 <build><!-- 指定最终构建产物的名称, 例如生成的 JAR 文件的名称 --><finalName>${artifactId}-${version}</finalName><!-- 指定源代码文件的目录路径 --><sourceDirectory>src/main/java</sourceDirectory>&l…...
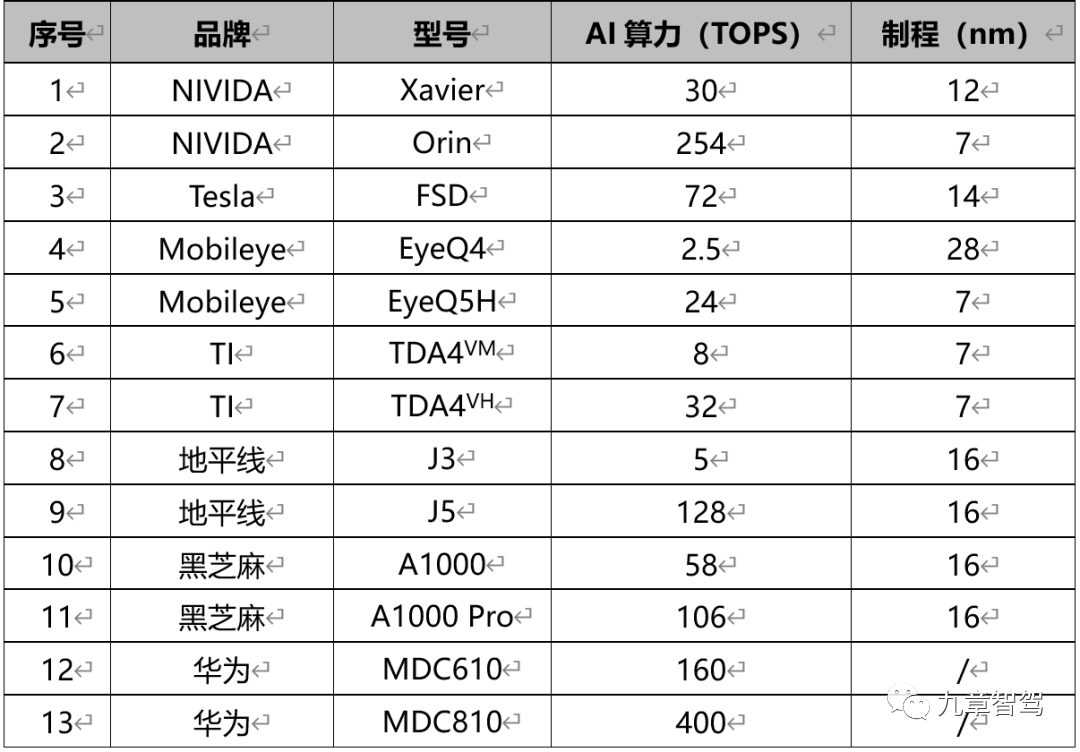
智能驾驶产品开发中如何贯彻“正向开发”理念
摘要: 基于演绎法的正向开发理念,能够让智能驾驶产品在充分满足用户需求,保证产品质量的同时,确保开发目标合理且得到落实。 前段时间,微博CEO吐槽理想L9智能驾驶“行驶轨迹不居中”,在网上引发了热烈讨论…...
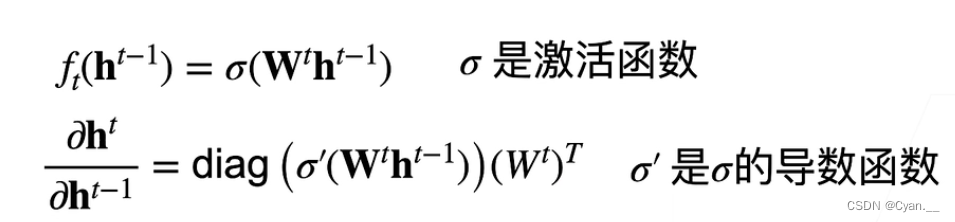
【机器学习】038_梯度消失、梯度爆炸
一、原因 神经网络梯度 假设现在有一个 层的神经网络,每层的输出为一个对输入作 变换的函数结果 用 来表示第 层的输出,那么有下列公式: 链式法则计算损失 关于某一层某个参数 的梯度: 注意到, 为向量&am…...
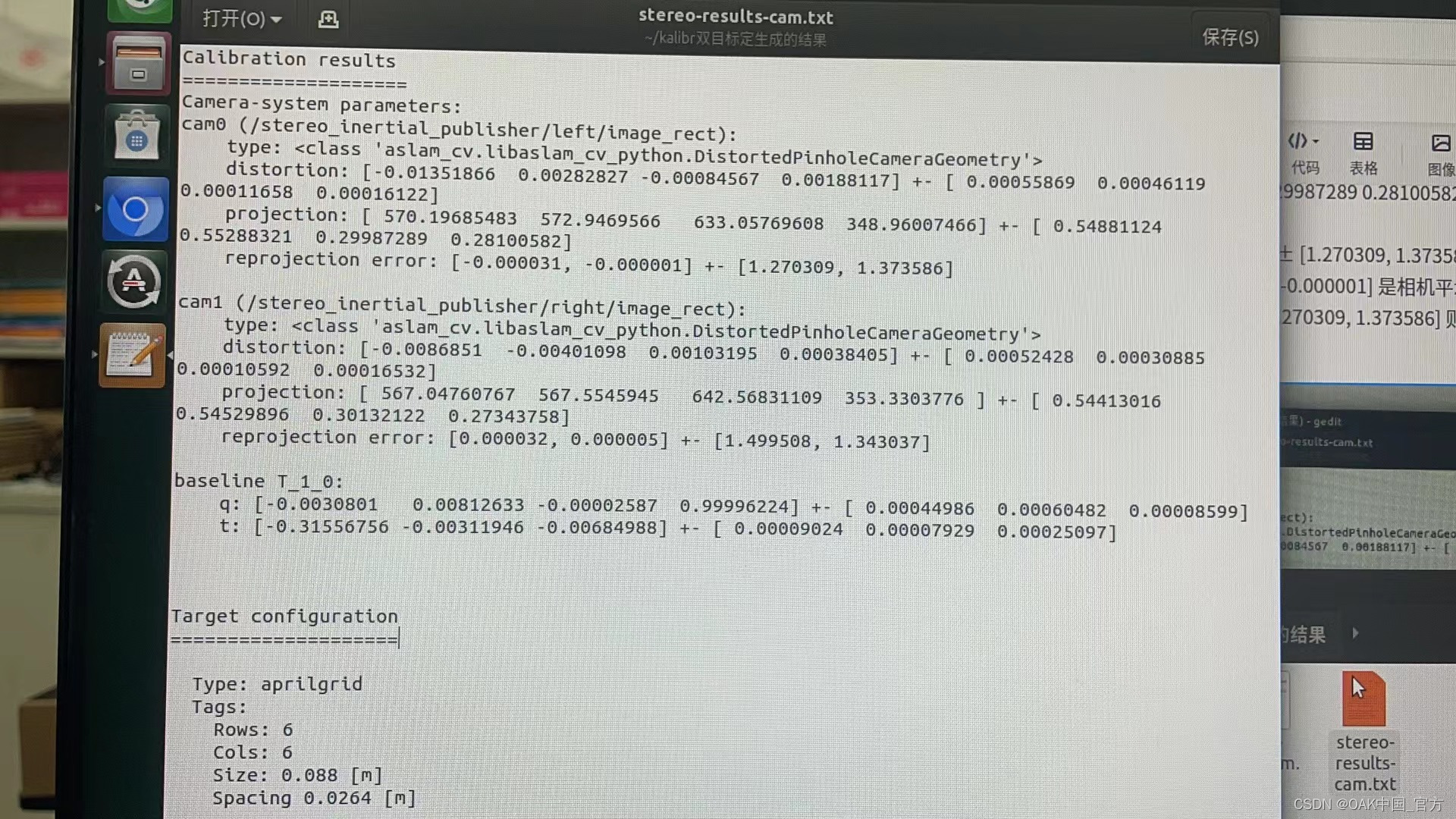
【转】OAK-D双目相机进行标定及标定结果说明
编辑:OAK中国 首发:A. hyhCSDN 喜欢的话,请多多👍⭐️✍ 内容来自用户的分享,如有疑问请与原作者交流! ▌前言 Hello,大家好,这里是OAK中国,我是助手君。 近期在CSDN刷…...

whip和whep
原文为runner365.git大佬的文章 原文链接:https://blog.csdn.net/sweibd/article/details/124552793 WHIP接口 什么是whip 全称: WebRTC-HTTP ingestion protocol (WHIP). rfc地址: rfc-draft-murillo-whip-00 简单说,就是通过HTTP接口能导入webrtc媒…...

SpringBoot集成jjwt和使用
1.引入jwt依赖(这里以jjwt为例,具体其他jwt产品可以参见jwt官网) <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.9.1</version> </dependency>…...

RedisConnectionFactory is required已解决!!!!
1.起因🤶🤶🤶🤶 redis搭建完成后,准备启动主程序,异常兴奋,结果报错了!!!! 2.究竟是何原因 😭😭😭…...

redis的高可用之持久化
1、redis的高可用考虑指标 (1)正常服务 (2)数据容量的扩展 (3)数据的安全性 2、redis实现高可用的四种方式 (1)持久化 (2)主从复制 (3&…...
onnx模型转换opset版本和固定动态输入尺寸
背景:之前我想把onnx模型从opset12变成opset12,太慌乱就没找着,最近找到了官网上有示例的,大爱onnx官网,分享给有需求没找着的小伙伴们。 1. onnx模型转换opset版本 官网示例: import onnx from onnx im…...
远程运维如何更高效的远程管理?向日葵的这几项功能会帮到你
远程运维如何更高效的远程管理?向日葵的这几项功能会帮到你 具备一定规模的企业,其IT运维需求普遍会面临设备数量众多、难以统一高效管理、始终存在安全敞口等问题,尤其是针对分部广泛的无人值守设备时,更是如此。 举一个简单的例…...

python BDD 的相关概念
在Python 语言中进行BDD的规格和测试文件的编写的时候,常常会遇到下面的概念: Fixture : 测试设施。设定测试环境的预设状态或值的机制。Background: 背景。所有场景的公共部分。Scenario: 场景。Given : 前置条件Whe…...

【Exception】Error: Dynamic require of “path“ is not supported
Talk is cheap, show me the code. 环境 | Environment kversionOSwindows 11Node.jsv18.14.2npm9.5.0vite5.0.0vue3.3.8 报错日志 | Error log >npm run dev> app10.0.0 dev > viteERROR failed to load config from C:\code\frontend\app1\vite.config.js …...

【蓝桥杯选拔赛真题25】C++两个数比大小 第十三届蓝桥杯青少年创意编程大赛C++编程选拔赛真题解析
目录 C/C++两个数比大小 一、题目要求 1、编程实现 2、输入输出 二、算法分析...
)
C++学习——C++运算符重载(含义、格式、示例、遵循的规则)
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 一、运算符重载的含义 所谓重载,就是赋予新的含义。函数重载(Function Overloading)可以让一个函数名有多种功能,在不同情况下进行不同…...

【unity实战】unity3D中的PRG库存系统和换装系统(附项目源码)
文章目录 先来看看最终效果前言素材简单绘制库存UI前往mixamo获取人物模型动画获取一些自己喜欢的装备物品模型库存系统换装系统装备偏移问题添加消耗品最终效果源码完结 先来看看最终效果 前言 之前2d的换装和库存系统我们都做过不少了,这次就来学习一个3d版本的&…...

编程语言发展史:C语言的诞生及其影响
预计更新 第一部分:早期编程语言 1.1布尔代数和机器语言 1.2汇编语言的出现和发展 1.3高级语言的兴起 第二部分:主流编程语言 1.1 C语言的诞生及其影响 1.2 C语言的发展和应用 1.3 Java语言的出现和发展 1.4 Python语言的兴起和特点 1.5 JavaScript语言…...
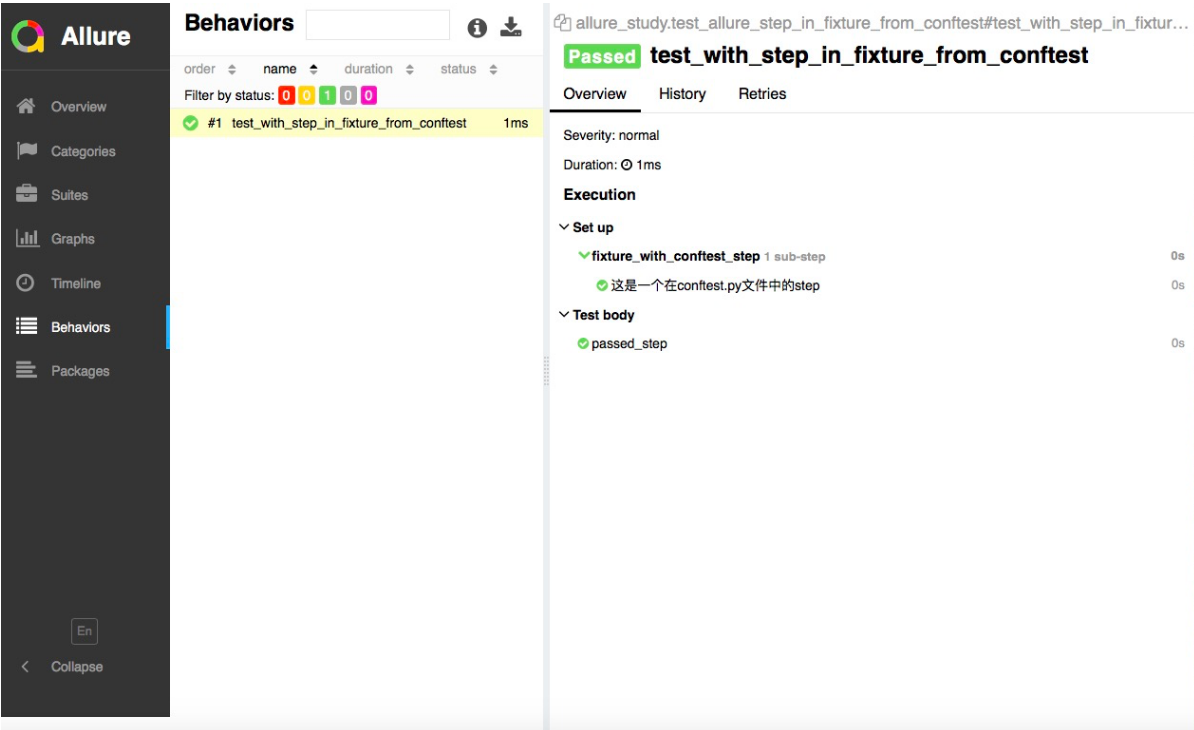
(二)pytest自动化测试框架之添加测试用例步骤(@allure.step())
前言 在编写自动化测试用例的时候经常会遇到需要编写流程性测试用例的场景,一般流程性的测试用例的测试步骤比较多,我们在测试用例中添加详细的步骤会提高测试用例的可阅读性。 allure提供的装饰器allure.step()是allure测试报告框架非常有用的功能&am…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
