2023亚太杯数学建模思路 - 案例:粒子群算法
文章目录
- 1 什么是粒子群算法?
- 2 举个例子
- 3 还是一个例子
- 算法流程
- 算法实现
- 建模资料
# 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 什么是粒子群算法?
粒子群算法(Particle Swarm Optimization,PSO)是一种模仿鸟群、鱼群觅食行为发展起来的一种进化算法。其概念简单易于编程实现且运行效率高、参数相对较少,应用非常广泛。粒子群算法于1995年提出,距今(2019)已有24年历史。
粒子群算法中每一个粒子的位置代表了待求问题的一个候选解。每一个粒子的位置在空间内的好坏由该粒子的位置在待求问题中的适应度值决定。每一个粒子在下一代的位置有其在这一代的位置与其自身的速度矢量决定,其速度决定了粒子每次飞行的方向和距离。在飞行过程中,粒子会记录下自己所到过的最优位置 P,群体也会更新群体所到过的最优位置G 。粒子的飞行速度则由其当前位置、粒子自身所到过的最优位置、群体所到过的最优位置以及粒子此时的速度共同决定。

2 举个例子
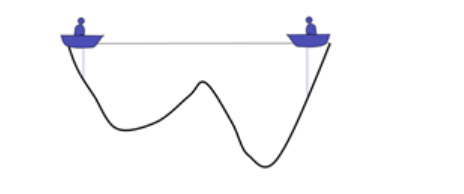
在一个湖中有两个人他们之间可以通信,并且可以探测到自己所在位置的最低点。初始位置如上图所示,由于右边比较深,因此左边的人会往右边移动一下小船。
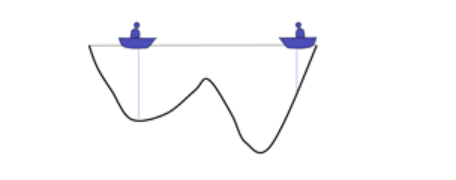
现在左边比较深,因此右边的人会往左边移动一下小船
一直重复该过程,最后两个小船会相遇
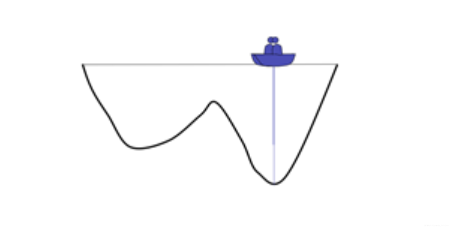
得到一个局部的最优解
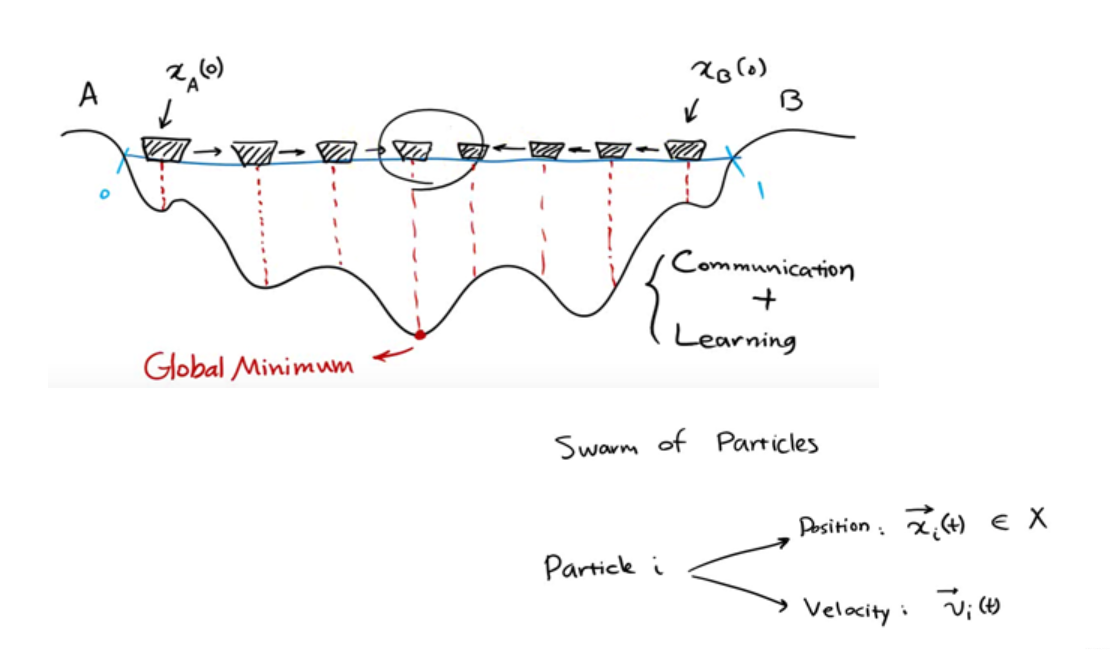 将每个个体表示为粒子。每个个体在某一时刻的位置表示为,x(t),方向表示为v(t)
将每个个体表示为粒子。每个个体在某一时刻的位置表示为,x(t),方向表示为v(t)
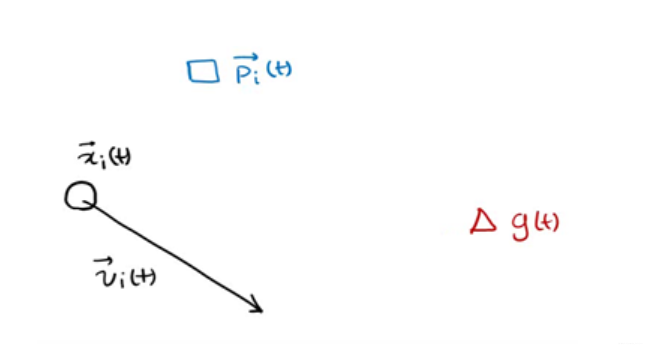
p(t)为在t时刻x个体的自己的最优解,g(t)为在t时刻所有个体的最优解,v(t)为个体在t时刻的方向,x(t)为个体在t时刻的位置
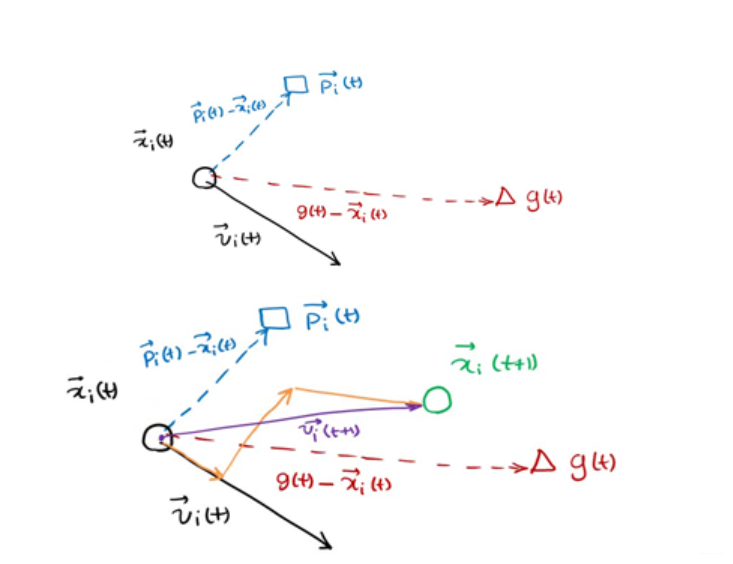
下一个位置为上图所示由x,p,g共同决定了
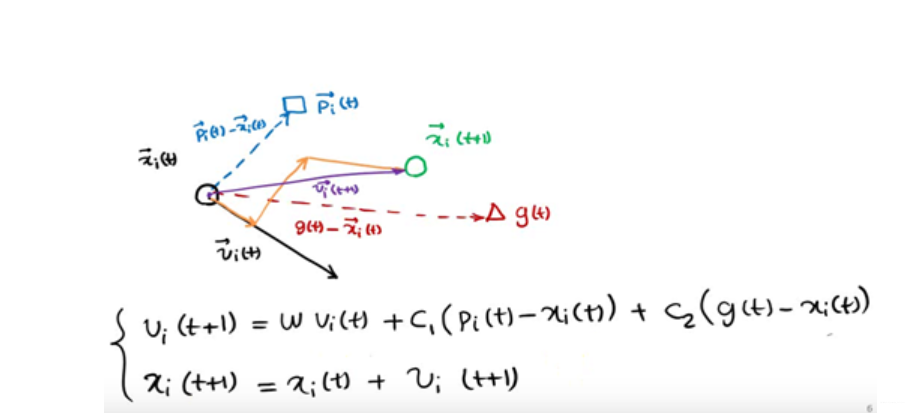
种群中的粒子通过不断地向自身和种群的历史信息进行学习,从而可以找到问题的最优解。
3 还是一个例子
粒子群算法是根据鸟群觅食行为衍生出的算法。现在,我们的主角换成是一群鸟。

小鸟们的目标很简单,要在这一带找到食物最充足的位置安家、休养生息。它们在这个地方的搜索策略如下:
1. 每只鸟随机找一个地方,评估这个地方的食物量。
2. 所有的鸟一起开会,选出食物量最多的地方作为安家的候选点G。
3. 每只鸟回顾自己的旅程,记住自己曾经去过的食物量最多的地方P。
4. 每只鸟为了找到食物量更多的地方,于是向着G飞行,但是呢,不知是出于选择困难症还是对P的留恋,或者是对G的不信任,小鸟向G飞行时,时不时也向P飞行,其实它自己也不知道到底是向G飞行的多还是向P飞行的多。
5. 又到了开会的时间,如果小鸟们决定停止寻找,那么它们会选择当前的G来安家;否则继续2->3->4->5来寻找它们的栖息地。
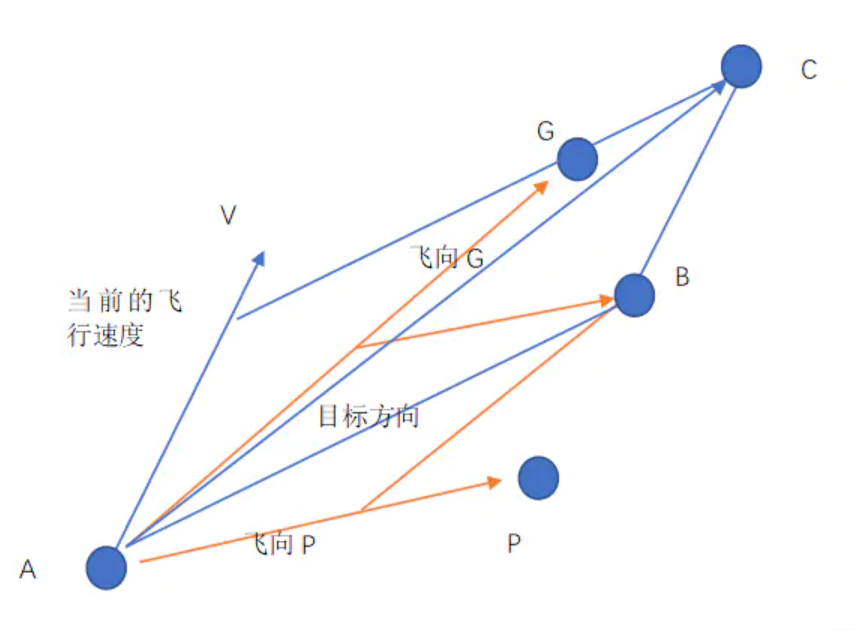
上图描述的策略4的情况,一只鸟在点A处,点G是鸟群们找到过的食物最多的位置,点P是它自己去过的食物最多的地点。V是它现在的飞行速度(速度是矢量,有方向和大小),现在它决定向着P和G飞行,但是这是一只佛系鸟,具体飞多少随缘。如果没有速度V,它应该飞到B点,有了速度V的影响,它的合速度最终使它飞到了点C,这里是它的下一个目的地。如果C比P好那么C就成了下一次的P,如果C比G好,那么就成了下一次的G。
算法流程
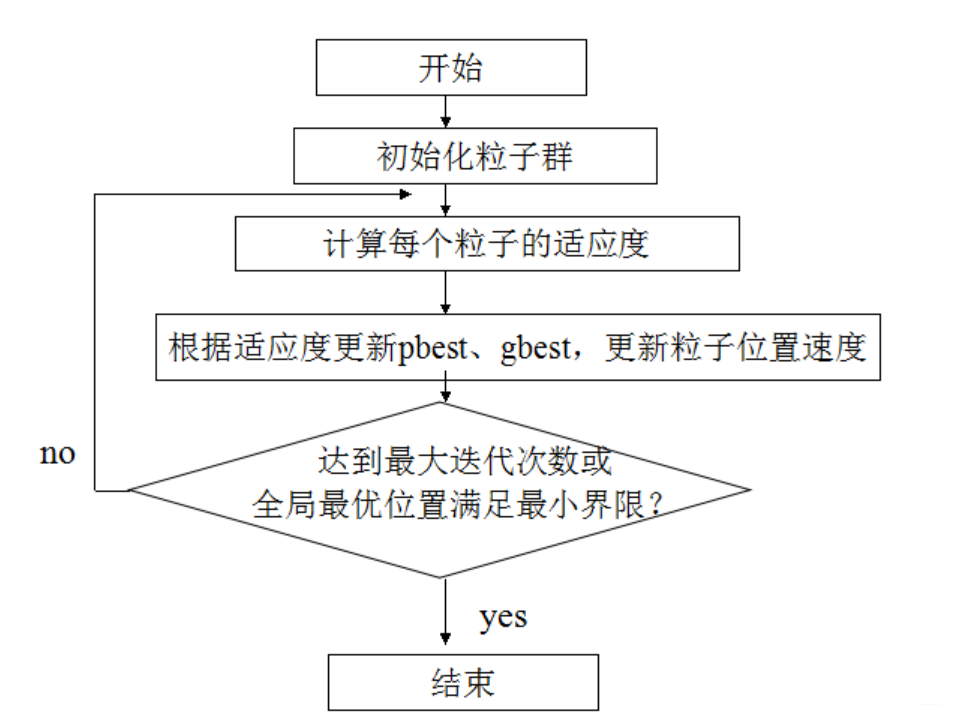
算法实现
这里学长用python来给大家演示使用粒子群解函数最优解
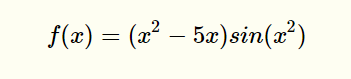
import numpy as np
import matplotlib.pyplot as plt
import random# 定义“粒子”类
class parti(object):def __init__(self, v, x):self.v = v # 粒子当前速度self.x = x # 粒子当前位置self.pbest = x # 粒子历史最优位置class PSO(object):def __init__(self, interval, tab='min', partisNum=10, iterMax=1000, w=1, c1=2, c2=2):self.interval = interval # 给定状态空间 - 即待求解空间self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值self.iterMax = iterMax # 迭代求解次数self.w = w # 惯性因子self.c1, self.c2 = c1, c2 # 学习因子self.v_max = (interval[1] - interval[0]) * 0.1 # 设置最大迁移速度#####################################################################self.partis_list, self.gbest = self.initPartis(partisNum) # 完成粒子群的初始化,并提取群体历史最优位置self.x_seeds = np.array(list(parti_.x for parti_ in self.partis_list)) # 提取粒子群的种子状态 ###self.solve() # 完成主体的求解过程self.display() # 数据可视化展示def initPartis(self, partisNum):partis_list = list()for i in range(partisNum):v_seed = random.uniform(-self.v_max, self.v_max)x_seed = random.uniform(*self.interval)partis_list.append(parti(v_seed, x_seed))temp = 'find_' + self.tabif hasattr(self, temp): # 采用反射方法提取对应的函数gbest = getattr(self, temp)(partis_list)else:exit('>>>tab标签传参有误:"min"|"max"<<<')return partis_list, gbestdef solve(self):for i in range(self.iterMax):for parti_c in self.partis_list:f1 = self.func(parti_c.x)# 更新粒子速度,并限制在最大迁移速度之内parti_c.v = self.w * parti_c.v + self.c1 * random.random() * (parti_c.pbest - parti_c.x) + self.c2 * random.random() * (self.gbest - parti_c.x)if parti_c.v > self.v_max: parti_c.v = self.v_maxelif parti_c.v < -self.v_max: parti_c.v = -self.v_max# 更新粒子位置,并限制在待解空间之内if self.interval[0] <= parti_c.x + parti_c.v <=self.interval[1]:parti_c.x = parti_c.x + parti_c.velse:parti_c.x = parti_c.x - parti_c.vf2 = self.func(parti_c.x)getattr(self, 'deal_'+self.tab)(f1, f2, parti_c) # 更新粒子历史最优位置与群体历史最优位置def func(self, x): # 状态产生函数 - 即待求解函数value = np.sin(x**2) * (x**2 - 5*x)return valuedef find_min(self, partis_list): # 按状态函数最小值找到粒子群初始化的历史最优位置parti = min(partis_list, key=lambda parti: self.func(parti.pbest))return parti.pbestdef find_max(self, partis_list):parti = max(partis_list, key=lambda parti: self.func(parti.pbest)) # 按状态函数最大值找到粒子群初始化的历史最优位置return parti.pbestdef deal_min(self, f1, f2, parti_):if f2 < f1: # 更新粒子历史最优位置parti_.pbest = parti_.xif f2 < self.func(self.gbest):self.gbest = parti_.x # 更新群体历史最优位置def deal_max(self, f1, f2, parti_):if f2 > f1: # 更新粒子历史最优位置parti_.pbest = parti_.xif f2 > self.func(self.gbest):self.gbest = parti_.x # 更新群体历史最优位置def display(self):print('solution: {}'.format(self.gbest))plt.figure(figsize=(8, 4))x = np.linspace(self.interval[0], self.interval[1], 300)y = self.func(x)plt.plot(x, y, 'g-', label='function')plt.plot(self.x_seeds, self.func(self.x_seeds), 'b.', label='seeds')plt.plot(self.gbest, self.func(self.gbest), 'r*', label='solution')plt.xlabel('x')plt.ylabel('f(x)')plt.title('solution = {}'.format(self.gbest))plt.legend()plt.savefig('PSO.png', dpi=500)plt.show()plt.close()if __name__ == '__main__':PSO([-9, 5], 'max')
效果
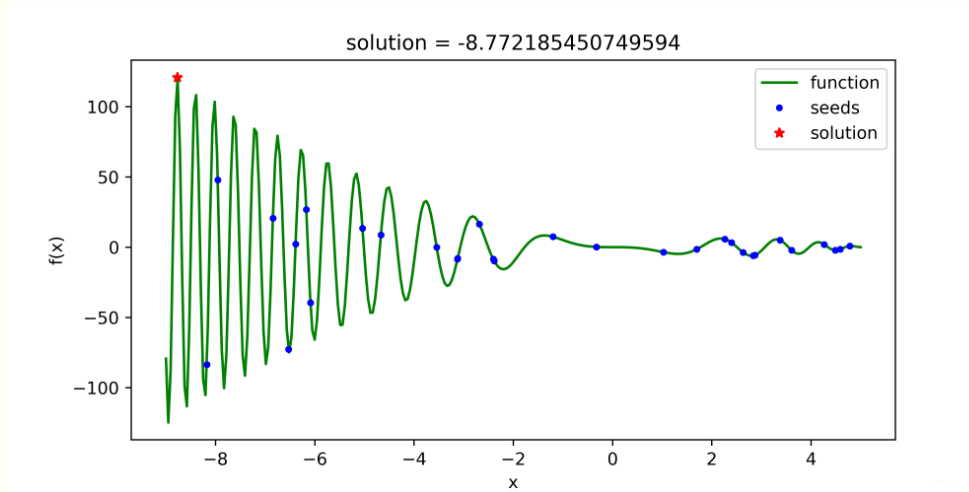
建模资料
资料分享: 最强建模资料


相关文章:

2023亚太杯数学建模思路 - 案例:粒子群算法
文章目录 1 什么是粒子群算法?2 举个例子3 还是一个例子算法流程算法实现建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 什么是粒子群算法? 粒子群算法(Pa…...

【开源】基于JAVA的开放实验室管理系统
项目编号: S 013 ,文末获取源码。 \color{red}{项目编号:S013,文末获取源码。} 项目编号:S013,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 实验室类型模块2.2 实验室模块2.3 实…...

LeetCode48旋转图像
思路是沿对角线交换元素,之后沿矩阵中线交换元素 参考链接 🔗:【LeetCode 每日一题】48. 旋转图像 | 手写图解版思路 代码讲解-哔哩哔哩】 class Solution {public void rotate(int[][] matrix) {int i0,j0;if(matrixnull){return;}int n matrix.length;// int[]…...
-墨者-url信息)
sql手工注入漏洞测试(MYSQL)-墨者-url信息
背景: 自己在墨者官网靶场练习的时候,一直出错,手工容易出错,所以列举一些信息供大家核对,可以参考改动。 数据库版本version() 5.7.22-0ubuntu0.16.04.1 当前数据库名称database() m…...
52.seata分布式事务
目录 1.事务的四大特性。 2.分布式服务的事务问题。 3.seata。 3.1理论基础。 3.1.1CAP定理。 3.1.2BASE理论。 3.2初识Seata。 3.2.1Seata的架构。 3.2.2部署TC服务。 3.2.3微服务集成Seata。 3.3 seata提供的四种分布式事务解决方案。 3.3.1 XA模式。 3.3.1.1 X…...

HTML所有功能大汇总
HTML所有的功能,都在下面的表格中呈现清楚了。千万不要死记硬背,但是在遇到困难的时候,可以按照这个表进行查找。 类别功能HTML标签文本样式粗体<b></b> 或 <strong></strong>斜体<i></i>或<em>&…...

层次分析法--可以帮助你做决策的简单算法
作用 层次分析法是一个多指标的评价算法,主要用来在做决策时,给目标的多个影响因子做权重评分。特别是那些需要主观决策的、或者需要用经验判断的决策方案,例如: 买房子(主观决策)选择旅游地(…...

docker启动链接sqlservr的镜像时报SSl错误
本次部署中遇到了老项目中的 net core 5.0 docker 镜像访问sql server 出现SSL Handshake failed with OpenSSL error - SSL_ERROR_SSL.问题 Microsoft.Data.SqlClient.SqlException (0x80131904): A connection was successfully established with the server, but then an e…...

力扣:175. 组合两个表(Python3)
题目: 表: Person ---------------------- | 列名 | 类型 | ---------------------- | PersonId | int | | FirstName | varchar | | LastName | varchar | ---------------------- personId 是该表的主键(具有唯一值的列&#…...
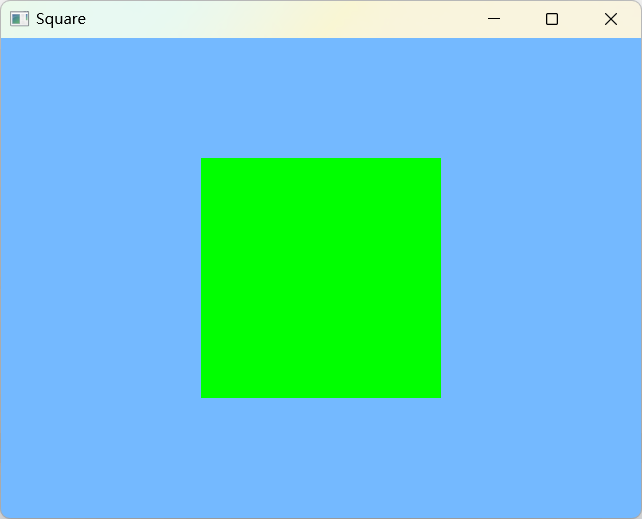
【libGDX】使用Mesh绘制矩形
1 前言 使用Mesh绘制三角形 中介绍了绘制三角形的方法,本文将介绍绘制正方形的方法。 libGDX 以点、线段、三角形为图元,没有提供绘制矩形内部的接口。要绘制矩形内部,必须通过三角形拼接而成,如下图,是通过GL_TRIANGL…...
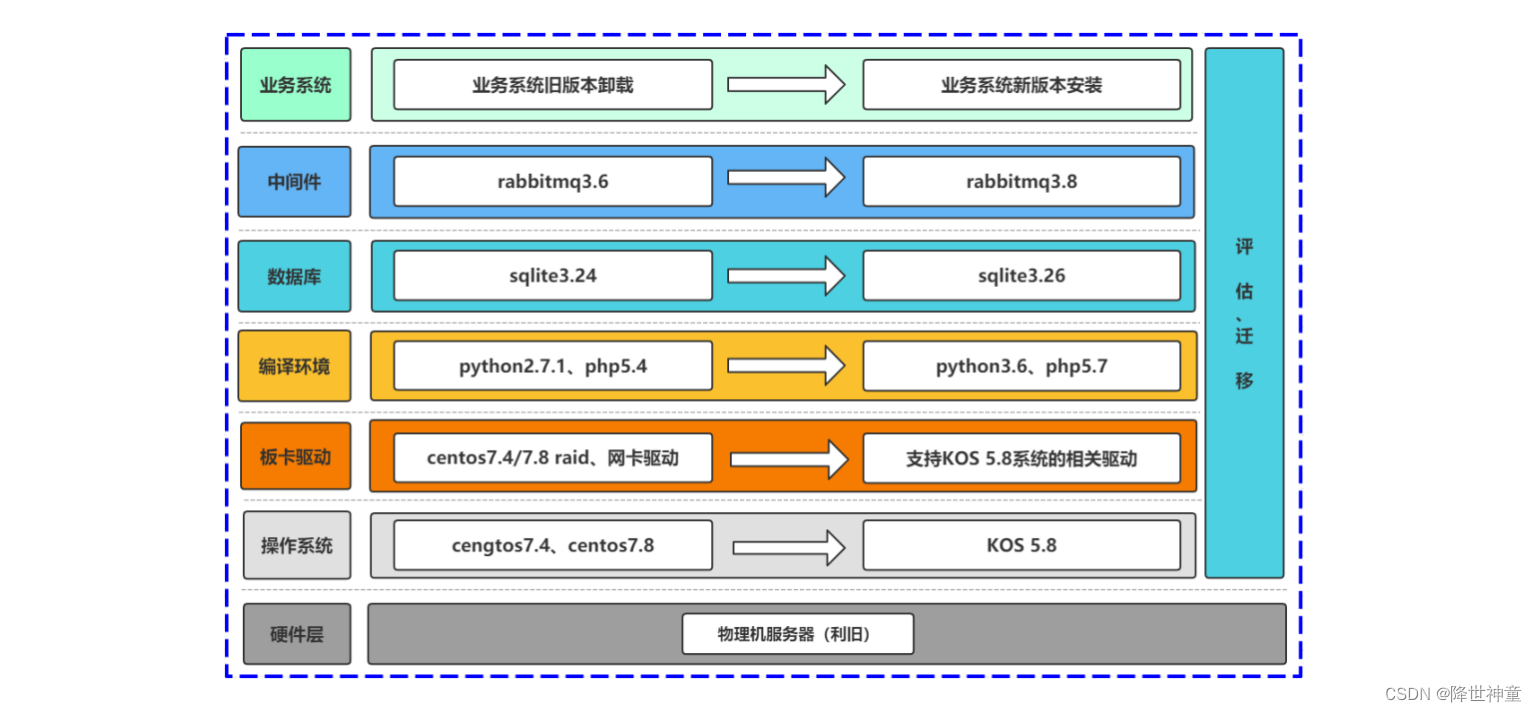
X2Keyarch迁移工具实战 | 将CentOS高效迁移至浪潮云峦操作系统KeyarchOS
X2Keyarch迁移工具实战 | 将CentOS高效迁移至浪潮云峦操作系统KeyarchOS 1. 搭建仿真线上业务环境2. 安装KeyarchOS操作系统和X2Keyarch迁移工具3. 将CentOS系统业务迁移至KeyarchOS系统 浪潮信息云峦操作系统KeyarchOS基于Linux Kernel、OpenAnolis等开源技术自主研发的一款服…...
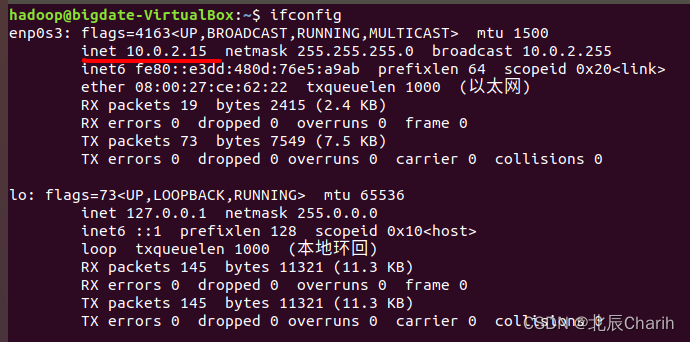
基于VM虚拟机下Ubuntu18.04系统,Hadoop的安装与详细配置
参考博客: https://blog.csdn.net/duchenlong/article/details/114597944 与上面这个博客几乎差不多,就是java环境配置以及后面的hadoop的hdfs-site.xml文件有一些不同的地方。 准备工作 1.更新 # 更新 sudo apt update sudo apt upgrade2.关闭防火…...
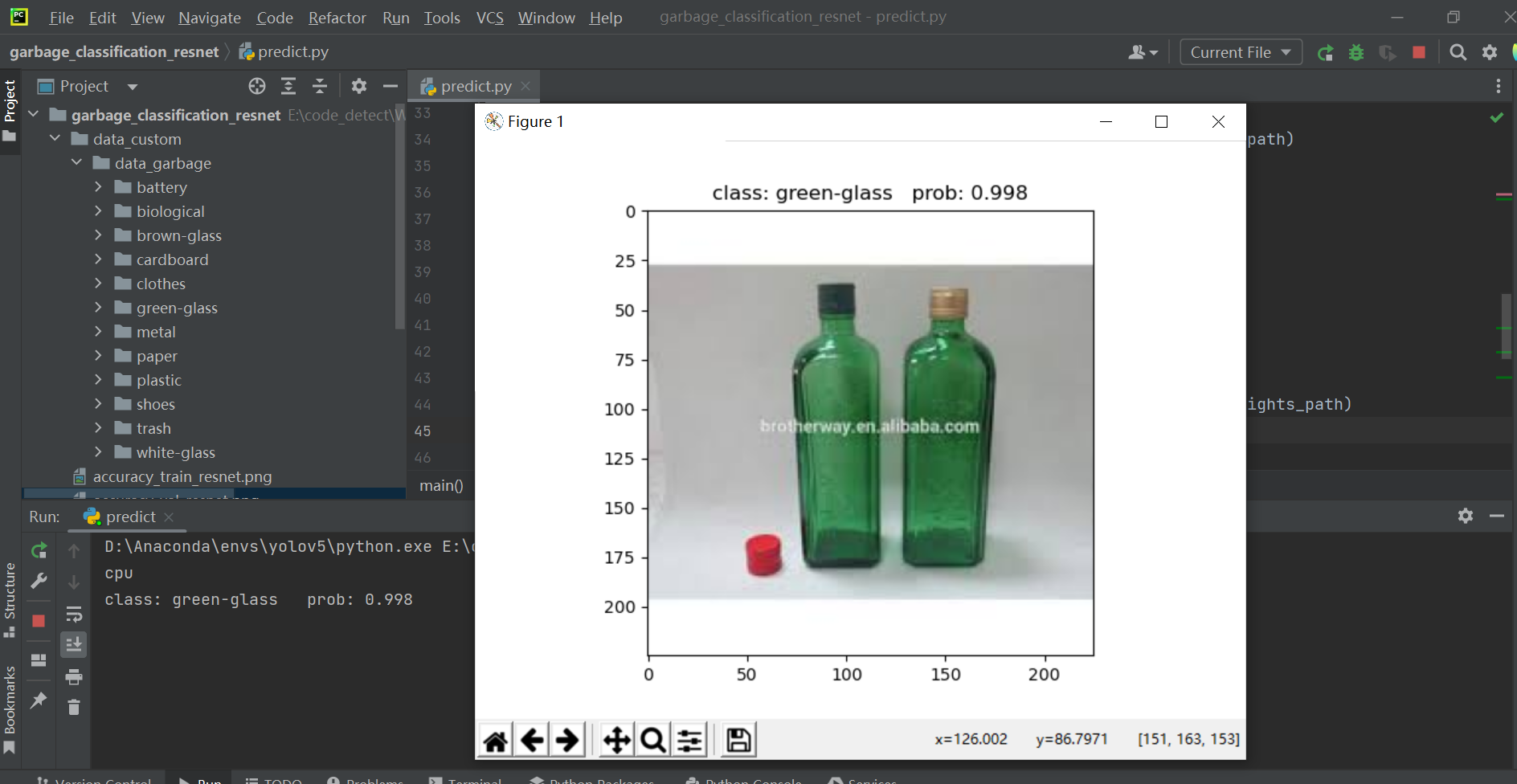
【图像分类】基于深度学习的垃圾分类系统的设计与实现(ResNet网络,附代码和数据集)
写在前面: 首先感谢兄弟们的关注和订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。(专栏订阅用户订阅专栏后免费提供数据集和源码一份,超级VIP用户不在服务范围之内,不想订阅专栏的兄弟们可以私信…...
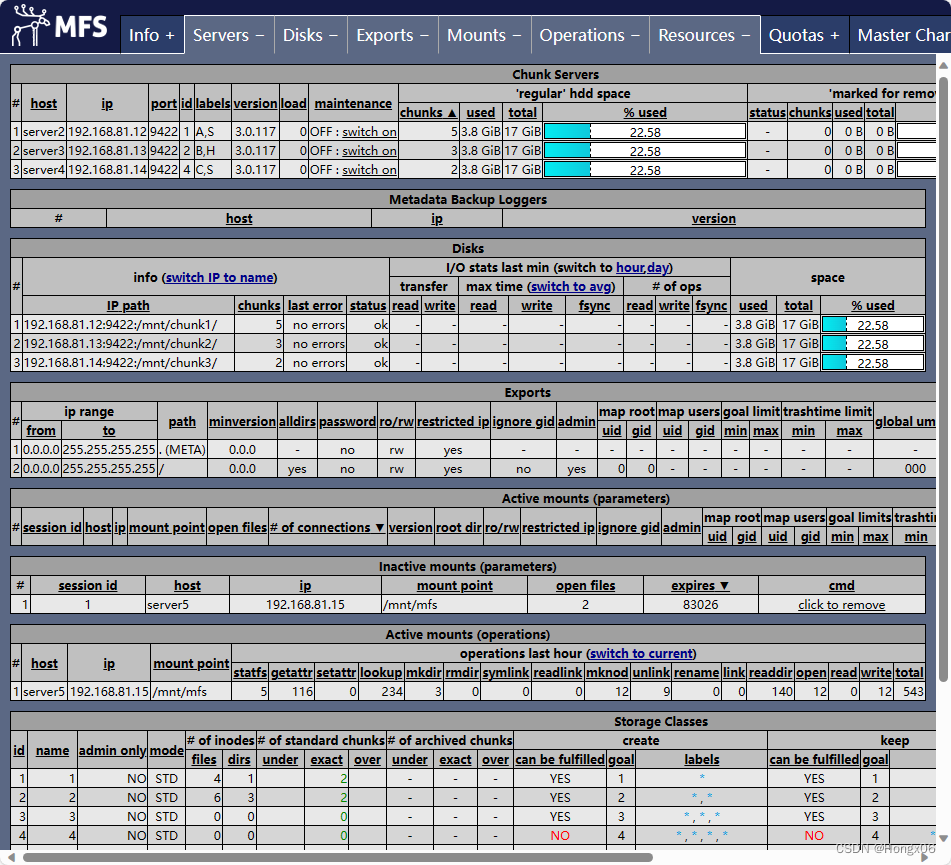
MFS分布式文件系统
目录 集群部署 Master Servers Chunkservers 编辑Clients Storage Classes LABEL mfs高可用 pacemaker高可用 编辑ISCSI 添加集群资源 主机 ip 角色 server1 192.168.81.11 Master Servers server2 192.168.81.12 Chunkservers server3 192.168.81.13 Chunkserver…...
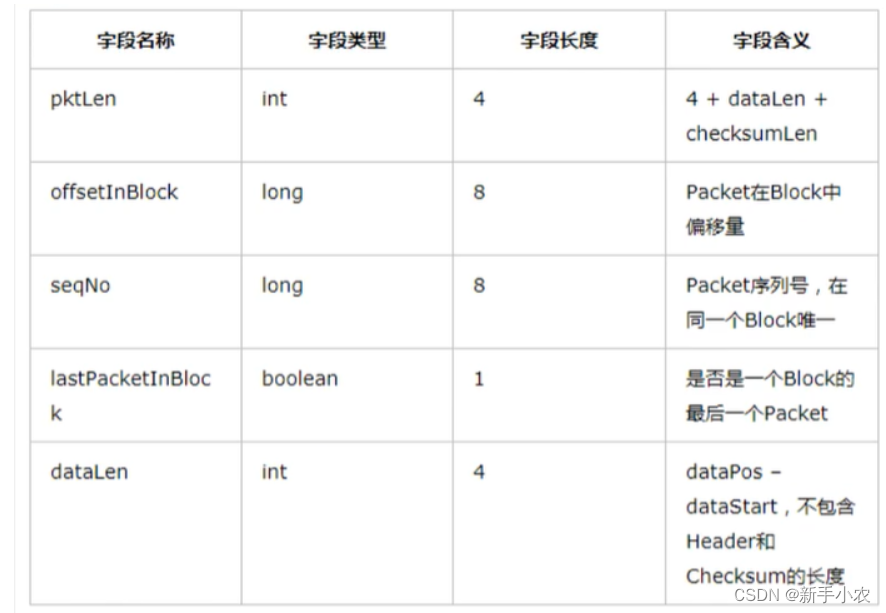
Hadoop -hdfs的读写请求
1、HDFS写数据(宏观): 1、首先,客户端发送一个写数据的请求,通过rpc与NN建立连接,NN会做一些简单的校验,文件是否存在,是否有空间存储数据等。 2、NN就会将校验的结果发送给客户端…...

【c++Leetcode】206. Reverse Linked List
问题入口 time complexity: O(n), space complexity:O(1) ListNode* reverseList(ListNode* head) {ListNode* prev nullptr;ListNode* curr head;while(curr){ListNode* forward curr->next;curr->next prev;prev curr;curr forward;}return prev; } time comp…...
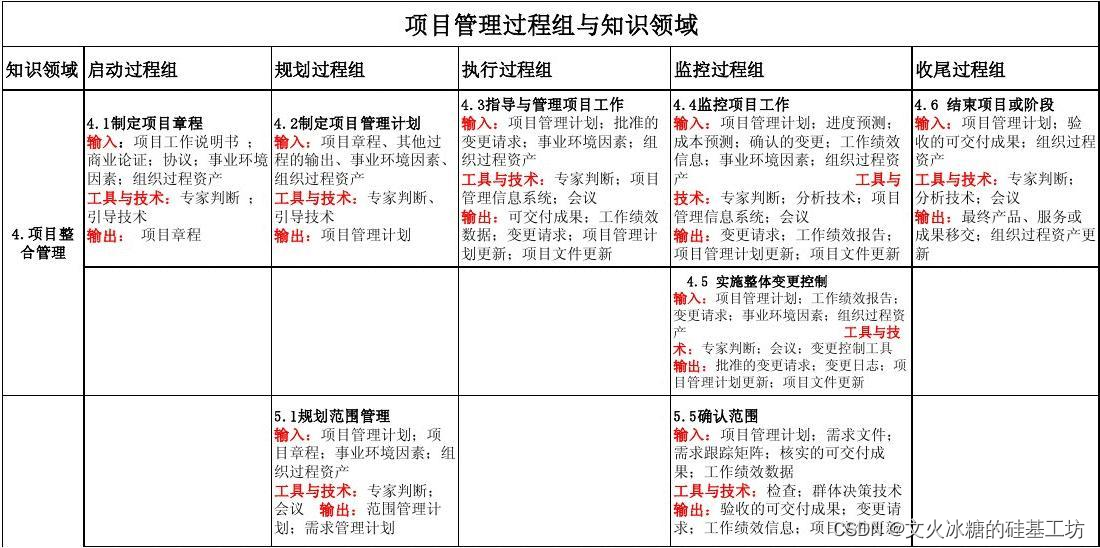
[项目管理-33/创业之路-87/管理者与领导者-127]:如何提升自己项目管理的能力和水平
目录 前言: 一、项目经理的角色定位 1.1 项目经理的职责 1.2 不同矩阵类型的项目,项目经理的职责 1.3 项目经理的角色定位 1.4 项目经理的发展路径 二、项目经理项目理论和知识结构 三、软件项目经理在计算机水平的提升 四、项目经理业务知识的…...

记录一次因内存不足而导致hiveserver2和namenode进程宕机的排查
背景 最近发现集群主节点总有进程宕机,定位了大半天才找到原因,分享一下 排查过程 查询hiveserver2和namenode日志,都是正常的,突然日志就不记录了,直到我重启之后又恢复工作了。 排查各种日志都是正常的࿰…...

c# 基础语法
c# 程序结构 using System.Collections.Generic; namespace demo1; //一个命名空间可以包含多个类 using System.IO; using System.Drawing;class proj {/// <summary>/// c#是微软开发的,基于c和c的一种面象对象编程语言,用于快速开发windows桌…...

【译】什么时候使用 Spring 6 JdbcClient
原文地址:Spring 6 JdbcClient: When and How to Use it? 一、前言 自 Spring 6.1 起,JdbcClient 为 JDBC 查询和更新操作提供了统一的客户端 API,从而提供了更流畅、更简化的交互模型。本教程演示了如何在各种场景中使用 JdbcClient。 二…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
