算法刷题-动态规划-1
不同路径


//机器人不同的路径进入到指定的地点
public static int uniquepath(int m, int n) {if (m <= 0 || n <= 0){return 0;}int[][] dp = new int[m][n];//初始化//如果只有i,j中有一个为0,那么机器人行走的方向只能有一种方式for (int i = 0; i < m; i++){dp[i][0] = 1;}for (itn i = 0; i < n; i++) {dp[0][i] = 1; }//推导出dp[m-1][n-1],因为定义dp[i][j]就是表示的是在[i][j]点 //不同的路径的数目 for (itn i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; }}return dp[m - 1][n - 1]; }
不同路径||



方法一:
大佬讲解
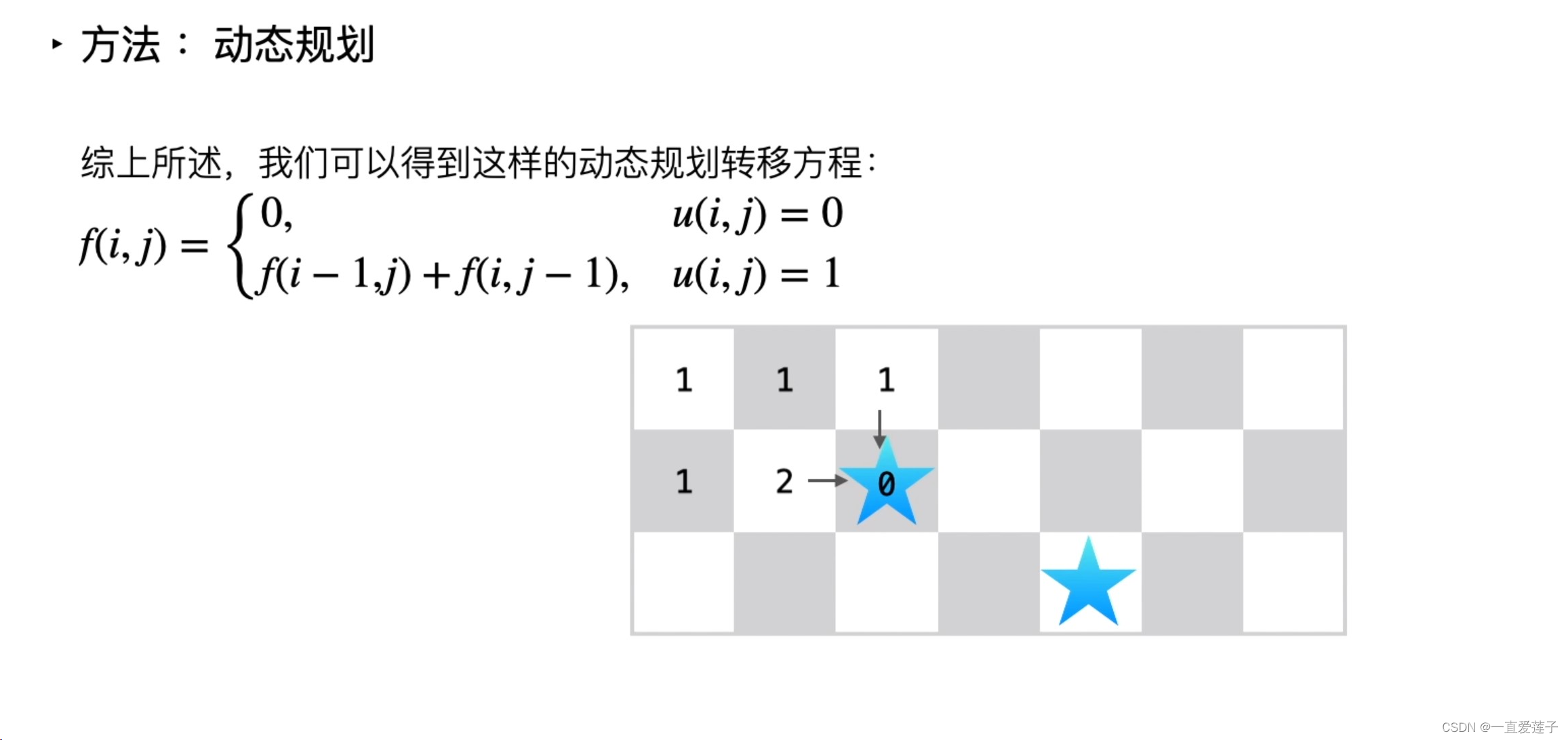
class Solution {
public:/*** 1. 确定dp数组下标含义 dp[i][j] 从(0,0)到(i,j)可能的路径种类;* 2. 递推公式 dp[i][j] = dp[i-1][j] + dp[i][j-1] 但是需要加限制条件就是没有障碍物的时候* if(obstacleGrid[i][j] == 0) dp[i][j] = dp[i-1][j] + dp[i][j-1];* 3. 初始化 当obstacleGrid[i][j] == 0时,dp[i][0]=1 dp[0][i]=1 初始化横竖就可;* 4. 遍历顺序 一行一行遍历;* 5. 推导结果;*/int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {/* 计算数组大小 */int m = obstacleGrid.size();int n = obstacleGrid[0].size();/* 定义dp数组 */vector<vector<int>> dp(m,vector<int>(n,0));/* 初始化dp数组 */for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++)dp[i][0] = 1; for(int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[0][i] = 1; /* 一行一行遍历 */ for(int i = 1; i < m; i++) { for(int j = 1; j < n; j++) { /* 去除障碍物 */ if(obstacleGrid[i][j] == 1) continue; dp[i][j] = dp[i-1][j] + dp[i][j-1]; }}return dp[m-1][n-1]; }
};方法二
多加一行和一列的虚拟节点,防止出现越界的情况,
把它们初始化成0,但是要保证第一个节点初始化成1.
dp[0][1] = 1;
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size(), n = obstacleGrid[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));dp[0][1] = 1;for(int i = 1; i <= m; i++) {for(int j = 1; j <= n; j++) {if(obstacleGrid[i - 1][j - 1] == 1) continue;else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m][n];}第N个泰波那契数

递归写法
1。先确定函数的一定是什么dp[ i ] 表示:第 i 个泰波那契数
2。题目中的关系代数是 dp[ i ] = dp[ i - 1 ] + dp[ i - 2 ] + dp[ i - 3。边界是T(0)=0,T(1)=1,T(2)=1T(0)=0, T(1)=1,
4。初始化为dp[ 0 ] = 0,dp[ 1 ] = 1,dp[ 2 ] = 1
class Solution {
public:int tribonacci(int n) {vector<int> dp(n + 1);if (n == 0) {return 0; }if (n <= 2) {return 1; }dp[0] = 0, dp[1] = 1, dp[2] = 1; for (int i = 3; i <= n; i++) { dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]; }return dp[n]; }
};
滚动数组
class Solution {
public:int tribonacci(int n) {if (n == 0) {return 0;}if (n <= 2) { return 1; }int p = 0, q = 0, r = 1, s = 1; for (int i = 3; i <= n; ++i) { p = q; q = r; r = s; s = p + q + r; }return s; }
};
三步问题

这就是老油条的步骤了,
先确定自己定义的函数,然后找出关系式,然后确定初始值
递归操作
class Solution {
public: int waysToStep(int n) { vector<in#t> dp(n + 1); const int MOD = 1e9 + 7; //边界问题 if (n == 1 || n == 2) return n; if (n == 3) return 4; //初始化定义 dp[1] = 1, dp[2] = 2, dp[3] = 4; for (int i = 4; i <= n; i++) { dp[i] = ((dp[i - 3] + dp[i - 2]) % MOD + dp[i - 1]) % MOD; }return dp[n]; }
};滚动数组
class Solution {
public: int waysToStep(int n) { int a=1,b=2,c=4,i; for(i=2;i<=n;i++){ long long t=(a+b)%1000000007; t=(t+c)%1000000007; a=b; b=c; c=t; }return a; }
};
使用最小画法爬楼梯


题目要求的是到达第n级台阶楼层顶部的最小花费,可以用动态规划来解,下面一步一步来讲怎样确定状态空间、怎样给出状态转移方程。
递归
-
大佬讲解
-
最近的一步有两种情况,
-
从 dp[ i - 1 ] 走一步过来,支付cost[ i - 1 ] 的费用; 1. 从 dp[ i - 1 ] 走一步过来,支付cost[ i - 1 ] 的费用;
-
从 dp[ i - 2 ] 走两步过来,支付cost[ i - 2 ] 的费用。
而 dp[ i ] 就是到达 i 位置的最小花费,
那我们就能得出状态转移方程:
dp [ i ] = min( dp[ i - 1 ] + cost[ i - 1 ],dp[ i - 2 ] + cost[ i - 2 ] )
class Solution {
public: int minCostClimbingStairs(vector<int>& cost) { int n = cost.size(); // 创建dp表,这样初始化默认填充的是 0 vector<int> dp(n + 1); for (int i = 2; i <= n; i++) { dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]); }return dp[n]; }
};
解码方法


方法一
动态规划的使用:
1。确立dp 数组的定义,代表的是 dp[i] 位置代表的是第i个位置时候解码方法的总数。
2。找关系代数=
-
s[ i ] 单独解码,如果是单独解码,当 s[ i ] 的值是 1~9 的时候可以自己解码,
自己解码的方案数就是 dp[ i - 1 ],如果 s[ i ] 的值是 0,那方案数就是0,整体解码失败, -
s[ i ] 和 s[ i - 1 ] 一起解码,当 s[ i - 1 ] * 10 + s[ i ] 的值是 10~26 的时候就可以解码,
而解码数就是 dp[ i - 2 ],如果解码失败,不在这个区间内,那方案数就也是0。
3。初始化dp数组,
初始化 dp[ 0 ] 和 dp[ 1 ] 位置,
dp[ 0 ] 位置,如果s[ 0 ] 解码成功就是1,不成功就是0
dp[ 1 ] 位置,如果 dp[ 1 ] 能自己解码,就 + 1,如果能跟 dp[ 0 ] 一起解码,就再 + 1,
如果dp[ 1 ] 两种情况都不能解码,就是0。(所以可能是0, 1, 2)
class Solution {
public:int numDecodings(string s) {int n = s.size();vector<int> dp(size);dp[0] = s[0] != '0';if (size == 1) return dp[0];if (s[0] != '0' && s[1] != '0') dp[1]++;int t = (s[0] - '0') * 10 + (s[1] - '0');if (t >= 10 && t <= 26) dp[1]++;for (int i = 2; i < size; i++) {if (s[i] != '0') dp[i] += dp[i - 1]; t = (s[i - 1] - '0') * 10 + (s[i] - '0');if (t >= 10 && t <= 26) dp[i] += dp[i - 2]; //一起解码}return dp[n - 1];}
};方法二:(大佬讲解)

class Solution {
public:int numDecodings(string s) {if (s[0] == '0') return 0;int n = s.size();vector<int> dp(n + 1, 1);//dp[0]表示s[-1]的状态, dp[1] 表示 s[0]的状态//dp[i] 表示 s[i-1]的状态for (int i = 2; i <= n; i++) {if (s[i - 1] == '0') {if (s[i - 2] == '1' || s[i - 2] == '2')//唯一译码,不增加情况dp[i] = dp[i - 2]; else//这里要好好理解一下,比如给定340, 输出可行的编码数为0, 因为0和40都无法转换 return 0; }else if (s[i - 2] == '1' || s[i - 2] == '2' && s[i - 1] >= '1' && s[i - 1] <= '6')dp[i] = dp[i - 1] + dp[i - 2]; else//当上述条件都不满足,维持上一个状态 dp[i] = dp[i - 1]; }//for(auto c:dp) cout << c << ","; return dp[n];//返回dp[n] 即最后 s[n-1] 的状态 }
};
相关文章:

算法刷题-动态规划-1
算法刷题-动态规划-1 不同路径不同路径||方法一:方法二 第N个泰波那契数递归写法滚动数组 三步问题递归操作滚动数组 使用最小画法爬楼梯递归 解码方法方法一方法二:(大佬讲解) 不同路径 //机器人不同的路径进入到指定的地点 publ…...
分享一篇很就以前的文档-VMware Vsphere菜鸟篇
PS:由于内容是很久以前做的记录,在整理过程中发现了一些问题,简单修改后分享给大家。首先ESXI节点和win7均运行在VMware Workstation上面,属于是最底层,而新创建的CentOS则是嵌套后创建的操作系统,这点希望…...

QT中的lambda表达式
面是对Qt中在QObject::connect()中的lambda表达式常用用法 QString str("I am a string!"); devicestr; connect(ui- connect(m_imgshowUI, &ImgShow::GetImgPath, m_visionplatform, [](const std::string filename){m_visionplatform->ReadImg(filename);}…...

linux文件I/O:文件锁的概念、函数以及代码实现
文件锁是一种用来保证多个进程对同一个文件的安全访问的机制。文件锁可以分为两种类型:建议性锁和强制性锁。建议性锁是一种协作式的锁,它只有在所有参与的进程都遵守锁的规则时才有效。强制性锁是一种强制式的锁,它由内核或文件系统来强制执…...
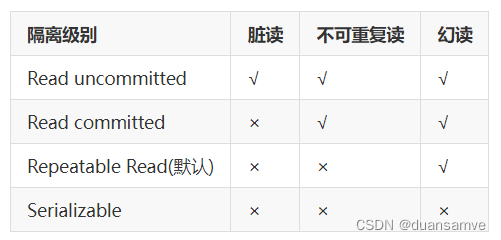
MySQL数据库系统教程
目录 基础篇 通用语法及分类 DDL(数据定义语言) 数据库操作 表操作 DML(数据操作语言) 添加数据 更新和删除数据 DQL(数据查询语言) 基础查询 条件查询 聚合查询(聚合函数࿰…...

这样写postman实现参数化,阿里p8都直呼牛逼
什么时候会用到参数化 比如:一个模块要用多组不同数据进行测试 验证业务的正确性 Login模块:正确的用户名,密码 成功;错误的用户名,正确的密码 失败 postman实现参数化 在实际的接口测试中,部分参数…...

【Qt-25】控件篇
一、comboBox控件 1、获取item数量 ui->comboBox_2->count(); 2、根据索引值获取文本 ui->comboBox->itemText(i); 3、调整当前显示文本内容 ui->comboBox->setCurrentIndex(j); 4、添加item ui->comboBox->addItem("");//添加一个内…...

《算法通关村——反转字符串中的单词问题解析》
《算法通关村——反转字符串中的单词问题解析》 151. 反转字符串中的单词 给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且 单词 之间用单个空格连接…...
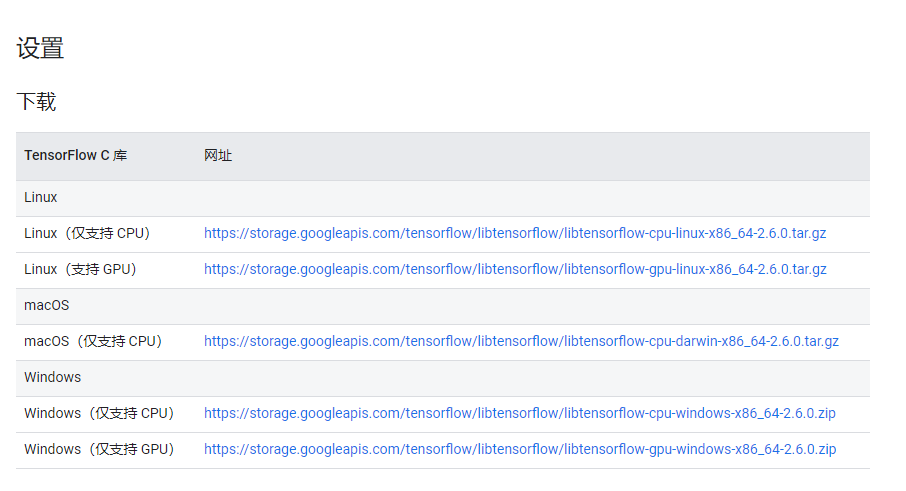
C++使用Tensorflow2.6训练好的模型进行预测
要在C语言中调用训练好的TensorFlow模型,需要使用TensorFlow C API。 https://tensorflow.google.cn/install/lang_c?hl=zh-cnten TensorFlow 提供了一个 C API,该 API 可用于为其他语言构建绑定。该 API 在 c_api.h 中定义,旨在实现简洁性和一致性,而不是便利性。 下载…...

5-1 Java 网络编程
第1关:URL类与InetAddress类 任务描述 本关任务:了解网络编程基础知识。 相关知识 为了完成本关任务,你需要掌握:1.URL;2.InetAddress。 URL 统一资源定位符(Uniform Resource Locator,缩…...

汇编-CALL和RET指令
CALL指令调用一个过程, 使处理器从新的内存位置开始执行。过程使用RET(从过程返回) 指令将处理器转回到该过程被调用的程序点上。 CALL指令的动作: 1.将CALL指令的下一条指令地址压栈(作为子过程返回的地址) 2.将被调过程的地址复制到指令指针寄存器E…...
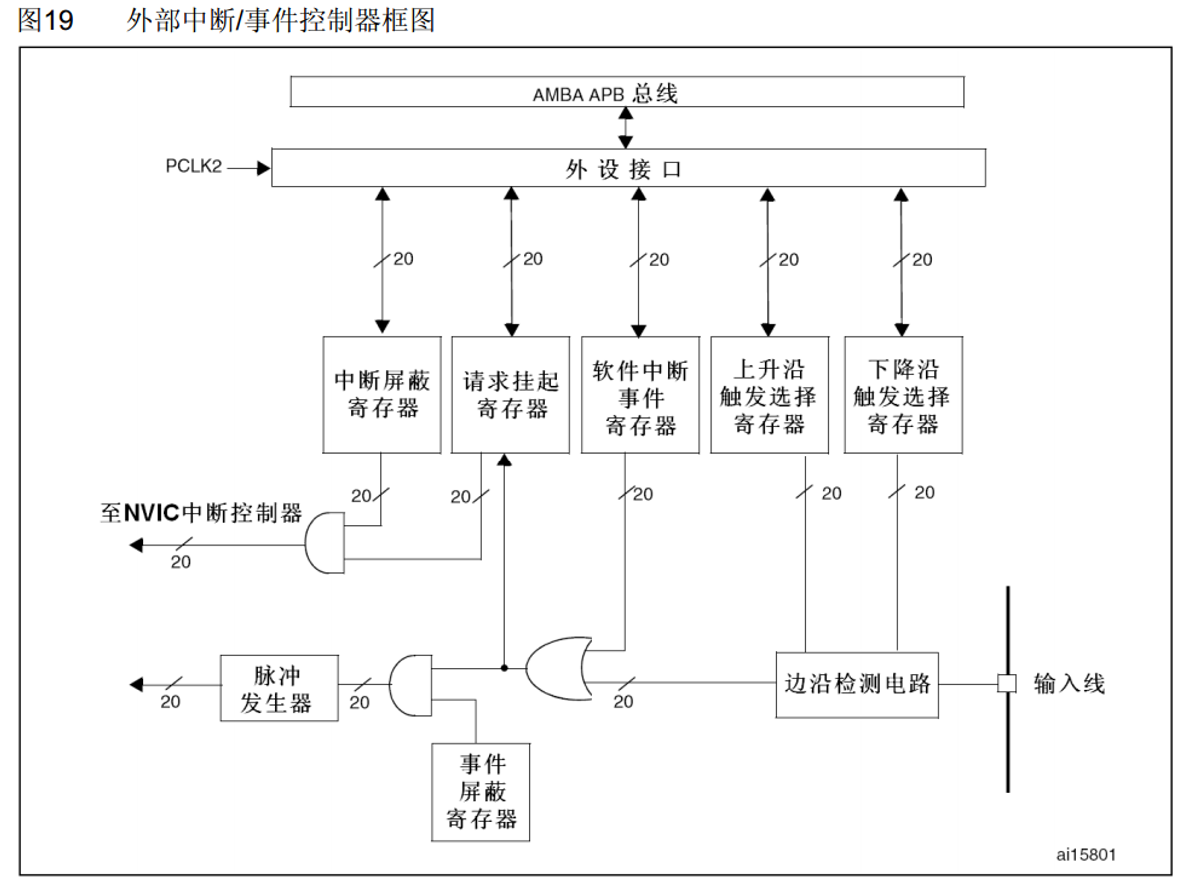
STM32_5(中断)
中断系统 中断:在主程序运行过程中,出现了特定的中断触发条件(中断源),使得CPU暂停当前正在运行的程序,转而去处理中断程序,处理完成后又返回原来被暂停的位置继续运行中断优先级:当…...

docker 部署hbase 并且java Api连接
首先先运行容器 docker run -d --name hbase -p 2181:2181 -p 16010:16010 -p16000:16000 -p 16020:16020 -p 16030:16030 harisekhon/hbase2.在本机的hosts中注册docker的id 因为docker内部集成了其他环境而其他环境 中的ip是docker id 所以需要在hosts中转换 192.168.80.120…...

EasyExcel listener无法通过Autowired注入xxMapper
easyexcel listener无法通过Autowired注入xxMapper 文章目录 easyexcel listener无法通过Autowired注入xxMapperbug记录:解决方案:easyexcel 使用例子controllerServiceImpllistener bug记录: productMapper注入一直为null,而procureDetailM…...

Android Spannable 使用注意事项
1、当前示例中间的 "评论",使用SpannableStringBuilder实现,点击评论会有高亮效果加粗,但再点击其它Bar时无法恢复默认样式。 2、因为SpannableString或SpannableStringBuilder中的效果是叠加的,恢复默认样式需要先移除…...
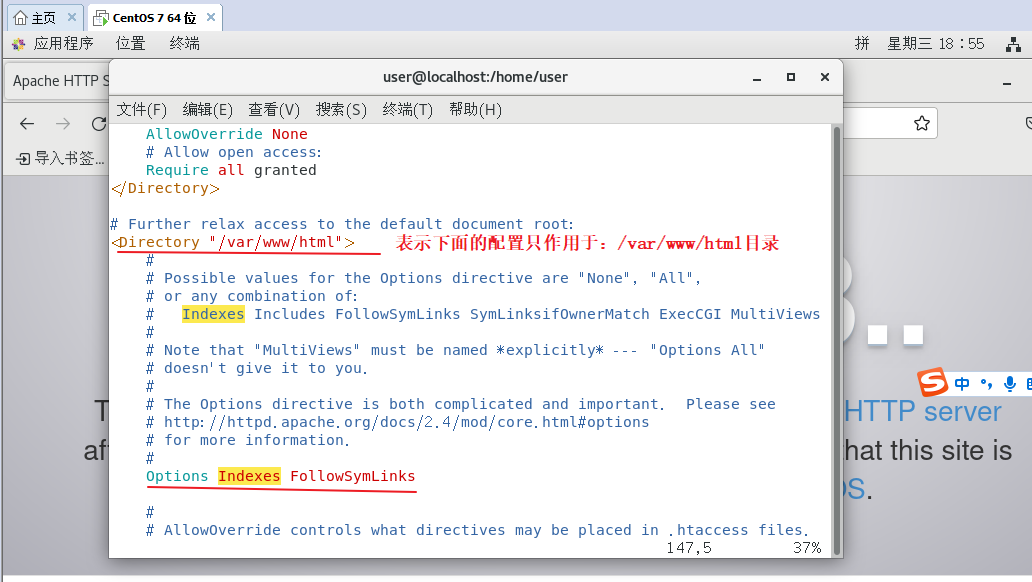
Apache访问控制
服务器相关的访问控制 Options指令 Options指令是Apache服务器配置文件中的一个重要指令,它可以用于控制特定目录启用哪些服务器特性。Options指令可以在Apache服务器的核心配置、虚拟主机配置、特定目录配置以及.htaccess文件中使用。 以下是一些常用的服务器特性选项: N…...

二、类与对象(二)
8 this指针 8.1 this指针的引入 我们先来定义一个日期的类Date: #include <iostream> using namespace std; class Date { public:void Init(int year, int month, int day){_year year;_month month;_day day;}void Print(){cout << _year <&l…...
Pytorch从零开始实战10
Pytorch从零开始实战——ResNet-50算法实战 本系列来源于365天深度学习训练营 原作者K同学 文章目录 Pytorch从零开始实战——ResNet-50算法实战环境准备数据集模型选择开始训练可视化模型预测总结 环境准备 本文基于Jupyter notebook,使用Python3.8,…...

设计模式-单例模式实战
目录 一、引言二、适用场景三、代码实战饿汉式单例模式懒汉式单例模式双重检查锁定单例模式静态内部类单例模式 四、实际应用举例Runtime解析 五、结论 一、引言 单例模式是一种创建型设计模式,用于确保一个类只有一个实例,且提供全局访问点以访问该实例…...

requests库出现AttributeError问题的修复与替代方法
在使用App Engine时,开发者们通常会面临需要发送爬虫ip请求的情况,而Python中的requests库是一个常用的工具,用于处理爬虫ip请求。然而,在某些情况下,开发者可能会遇到一个名为AttributeError的问题,特别是…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
