openssl+ SM2 + linux 签名校验开发实例(C++)
文章目录
- 一、SM2校验理论基础
- 二、SM2签名校验开发实例(C++)
一、SM2校验理论基础
SM2的校验过程是使用椭圆曲线上的公钥验证签名的有效性。以下是SM2校验的理论基础相关知识点:
-
SM2签名算法: SM2的校验基于椭圆曲线数字签名算法(ECDSA)。在签名算法中,签名者使用私钥对消息的哈希值进行签名,而验证者使用相应的公钥、签名值和消息的哈希值进行验证。
-
公钥验证签名: SM2签名校验的核心在于使用签名者的公钥对签名值进行验证。只有持有私钥的一方才能够生成有效的签名,而任何人都可以使用相应的公钥验证签名的有效性。
-
椭圆曲线运算: 校验过程中涉及到椭圆曲线上的数学运算,包括点的加法、点的乘法等。这些运算是基于椭圆曲线离散对数问题的难解性来保障安全性。
-
消息摘要算法: SM2签名使用消息摘要算法对原始消息进行哈希,通常采用SM3算法。在校验过程中,验证者也需要使用相同的哈希算法对接收到的消息进行哈希。
-
椭圆曲线的离散对数问题: ECC的安全性基于椭圆曲线上的离散对数问题的难解性。在校验过程中,验证者需要执行椭圆曲线运算,确保签名值与消息的哈希值匹配。
-
SM2校验流程:
- 选择椭圆曲线参数。
- 生成公钥。
- 获取签名值、消息的哈希值和公钥。
- 使用椭圆曲线运算验证签名的有效性。
-
随机数生成: 随机数的生成在签名的校验中通常不涉及,因为验证者只需要使用公钥进行椭圆曲线运算。
-
校验结果: 如果校验成功,说明签名是由持有相应私钥的一方生成的,消息在传输过程中没有被篡改,校验者可以信任消息的完整性和真实性。
理解这些基础知识点有助于深入了解SM2校验的工作原理和安全性。在实际应用中,确保正确管理公钥,处理错误和异常情况,并根据具体需求进行适当的安全性考虑。
二、SM2签名校验开发实例(C++)
在Linux环境下使用C++和OpenSSL库进行SM2签名校验的示例代码如下。请注意,这里的公钥和签名数据是预先准备好的,你需要替换为你实际的公钥、签名和消息哈希值。
#include <openssl/evp.h>
#include <openssl/sm2.h>
#include <openssl/pem.h>int main() {EVP_PKEY* pubKey = EVP_PKEY_new();FILE* publicKeyFile = fopen("public_key.pem", "r");// 从文件中加载公钥if (!PEM_read_PUBKEY(publicKeyFile, &pubKey, NULL, NULL)) {perror("Error loading public key");return 1;}fclose(publicKeyFile);// 待验证的签名const char* signatureHex = "3046022100...";const char* messageHex = "e1e2a1...";// 将十六进制的签名和消息哈希值转换为二进制数据unsigned char* signature;unsigned char* messageHash;size_t sigLen, hashLen;sigLen = strlen(signatureHex) / 2;hashLen = strlen(messageHex) / 2;signature = (unsigned char*)malloc(sigLen);messageHash = (unsigned char*)malloc(hashLen);if (!signature || !messageHash) {perror("Memory allocation error");return 1;}if (hex2bin(signatureHex, signature, sigLen) != 0 ||hex2bin(messageHex, messageHash, hashLen) != 0) {perror("Error converting hex to binary");free(signature);free(messageHash);return 1;}// 创建 SM2 验签上下文EVP_MD_CTX* ctx = EVP_MD_CTX_new();EVP_MD_CTX_init(ctx);// 选择 SM3 摘要算法const EVP_MD* md = EVP_sm3();// 初始化验签if (!EVP_DigestVerifyInit(ctx, NULL, md, NULL, pubKey)) {perror("Error initializing verification");free(signature);free(messageHash);return 1;}// 添加待验证的消息if (!EVP_DigestVerifyUpdate(ctx, messageHash, hashLen)) {perror("Error updating verification");free(signature);free(messageHash);return 1;}// 执行验签int result = EVP_DigestVerifyFinal(ctx, signature, sigLen);// 输出验签结果if (result == 1) {printf("Signature verification successful\n");} else {printf("Signature verification failed\n");}// 释放资源EVP_MD_CTX_free(ctx);EVP_PKEY_free(pubKey);free(signature);free(messageHash);return 0;
}
请确保替换public_key.pem、signatureHex和messageHex为你实际使用的公钥文件、签名和消息哈希值。这个示例中的hex2bin函数用于将十六进制字符串转换为二进制数据,你可以根据需要实现或使用现有的实现。
相关文章:
)
openssl+ SM2 + linux 签名校验开发实例(C++)
文章目录 一、SM2校验理论基础二、SM2签名校验开发实例(C) 一、SM2校验理论基础 SM2的校验过程是使用椭圆曲线上的公钥验证签名的有效性。以下是SM2校验的理论基础相关知识点: SM2签名算法: SM2的校验基于椭圆曲线数字签名算法&a…...

有关Vue、微信小程序、UniApp中的CSS中的宽度width单位、自适应
在Vue中,可以使用以下单位来设置宽度(width) 像素(px):最常用的单位,表示一个绝对长度单位。例如,width: 200px; 表示宽度为200像素。百分比(%):…...
黑马React18: ReactRouter
黑马React: ReactRouter Date: November 21, 2023 Sum: React路由基础、路由导航、导航传参、嵌套路由配置 路由快速上手 1. 什么是前端路由 一个路径 path 对应一个组件 component 当我们在浏览器中访问一个 path 的时候,path 对应的组件会在页面中进行渲染 2. …...

算法刷题-动态规划-1
算法刷题-动态规划-1 不同路径不同路径||方法一:方法二 第N个泰波那契数递归写法滚动数组 三步问题递归操作滚动数组 使用最小画法爬楼梯递归 解码方法方法一方法二:(大佬讲解) 不同路径 //机器人不同的路径进入到指定的地点 publ…...
分享一篇很就以前的文档-VMware Vsphere菜鸟篇
PS:由于内容是很久以前做的记录,在整理过程中发现了一些问题,简单修改后分享给大家。首先ESXI节点和win7均运行在VMware Workstation上面,属于是最底层,而新创建的CentOS则是嵌套后创建的操作系统,这点希望…...

QT中的lambda表达式
面是对Qt中在QObject::connect()中的lambda表达式常用用法 QString str("I am a string!"); devicestr; connect(ui- connect(m_imgshowUI, &ImgShow::GetImgPath, m_visionplatform, [](const std::string filename){m_visionplatform->ReadImg(filename);}…...

linux文件I/O:文件锁的概念、函数以及代码实现
文件锁是一种用来保证多个进程对同一个文件的安全访问的机制。文件锁可以分为两种类型:建议性锁和强制性锁。建议性锁是一种协作式的锁,它只有在所有参与的进程都遵守锁的规则时才有效。强制性锁是一种强制式的锁,它由内核或文件系统来强制执…...
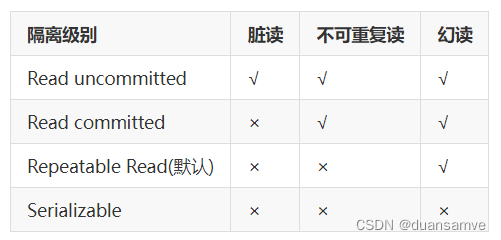
MySQL数据库系统教程
目录 基础篇 通用语法及分类 DDL(数据定义语言) 数据库操作 表操作 DML(数据操作语言) 添加数据 更新和删除数据 DQL(数据查询语言) 基础查询 条件查询 聚合查询(聚合函数࿰…...

这样写postman实现参数化,阿里p8都直呼牛逼
什么时候会用到参数化 比如:一个模块要用多组不同数据进行测试 验证业务的正确性 Login模块:正确的用户名,密码 成功;错误的用户名,正确的密码 失败 postman实现参数化 在实际的接口测试中,部分参数…...

【Qt-25】控件篇
一、comboBox控件 1、获取item数量 ui->comboBox_2->count(); 2、根据索引值获取文本 ui->comboBox->itemText(i); 3、调整当前显示文本内容 ui->comboBox->setCurrentIndex(j); 4、添加item ui->comboBox->addItem("");//添加一个内…...

《算法通关村——反转字符串中的单词问题解析》
《算法通关村——反转字符串中的单词问题解析》 151. 反转字符串中的单词 给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且 单词 之间用单个空格连接…...
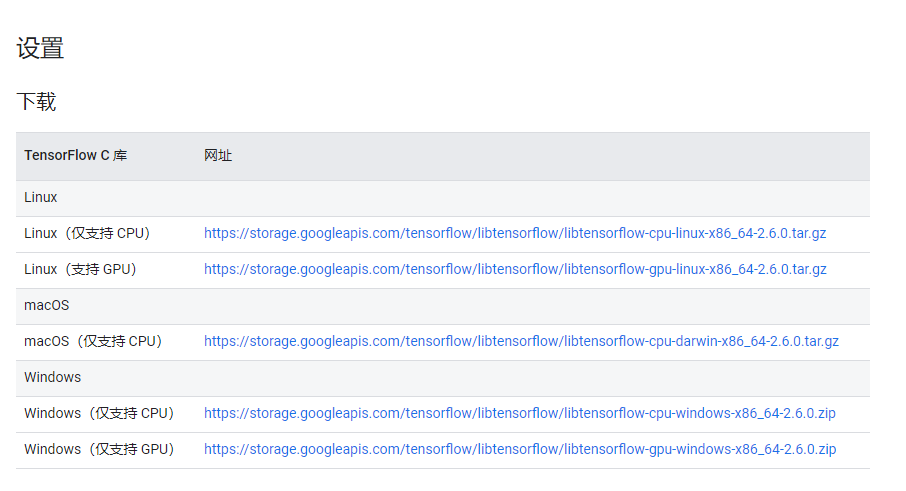
C++使用Tensorflow2.6训练好的模型进行预测
要在C语言中调用训练好的TensorFlow模型,需要使用TensorFlow C API。 https://tensorflow.google.cn/install/lang_c?hl=zh-cnten TensorFlow 提供了一个 C API,该 API 可用于为其他语言构建绑定。该 API 在 c_api.h 中定义,旨在实现简洁性和一致性,而不是便利性。 下载…...

5-1 Java 网络编程
第1关:URL类与InetAddress类 任务描述 本关任务:了解网络编程基础知识。 相关知识 为了完成本关任务,你需要掌握:1.URL;2.InetAddress。 URL 统一资源定位符(Uniform Resource Locator,缩…...

汇编-CALL和RET指令
CALL指令调用一个过程, 使处理器从新的内存位置开始执行。过程使用RET(从过程返回) 指令将处理器转回到该过程被调用的程序点上。 CALL指令的动作: 1.将CALL指令的下一条指令地址压栈(作为子过程返回的地址) 2.将被调过程的地址复制到指令指针寄存器E…...
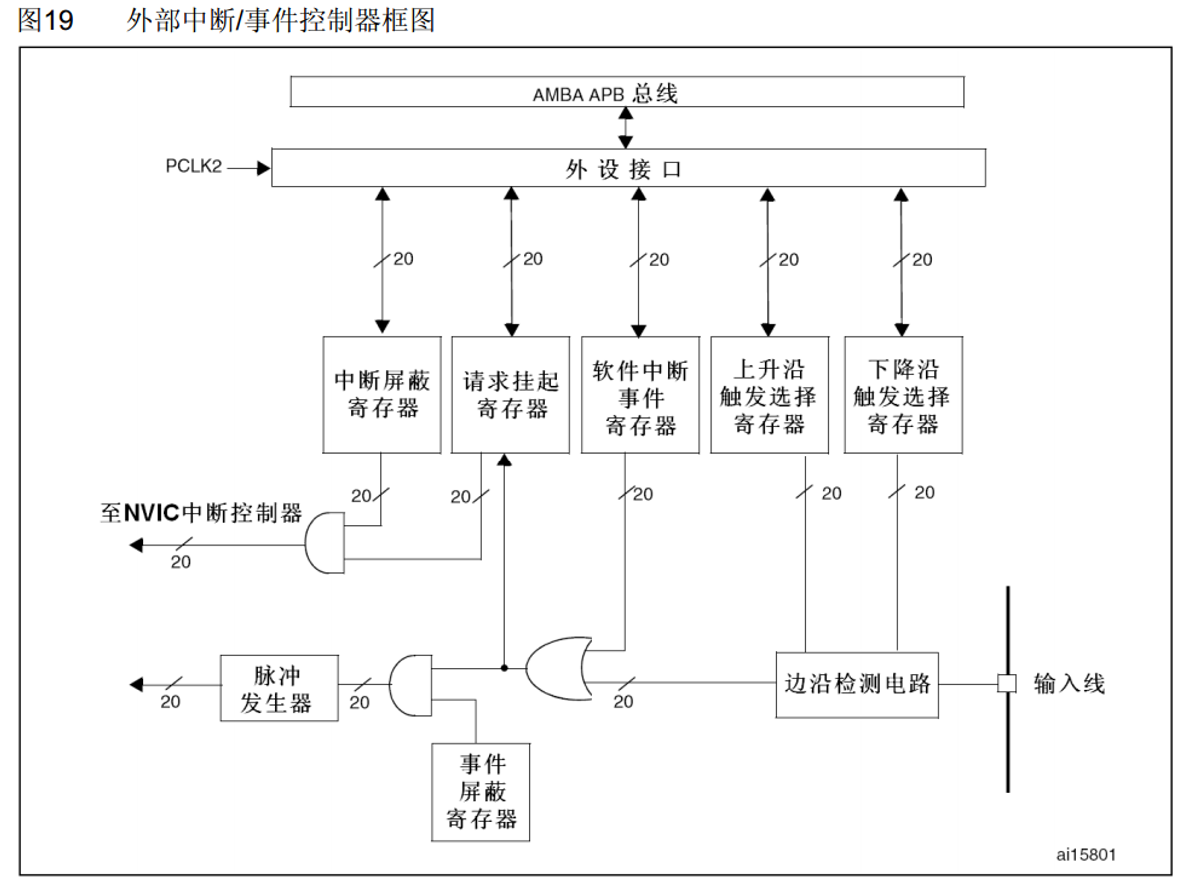
STM32_5(中断)
中断系统 中断:在主程序运行过程中,出现了特定的中断触发条件(中断源),使得CPU暂停当前正在运行的程序,转而去处理中断程序,处理完成后又返回原来被暂停的位置继续运行中断优先级:当…...

docker 部署hbase 并且java Api连接
首先先运行容器 docker run -d --name hbase -p 2181:2181 -p 16010:16010 -p16000:16000 -p 16020:16020 -p 16030:16030 harisekhon/hbase2.在本机的hosts中注册docker的id 因为docker内部集成了其他环境而其他环境 中的ip是docker id 所以需要在hosts中转换 192.168.80.120…...

EasyExcel listener无法通过Autowired注入xxMapper
easyexcel listener无法通过Autowired注入xxMapper 文章目录 easyexcel listener无法通过Autowired注入xxMapperbug记录:解决方案:easyexcel 使用例子controllerServiceImpllistener bug记录: productMapper注入一直为null,而procureDetailM…...

Android Spannable 使用注意事项
1、当前示例中间的 "评论",使用SpannableStringBuilder实现,点击评论会有高亮效果加粗,但再点击其它Bar时无法恢复默认样式。 2、因为SpannableString或SpannableStringBuilder中的效果是叠加的,恢复默认样式需要先移除…...
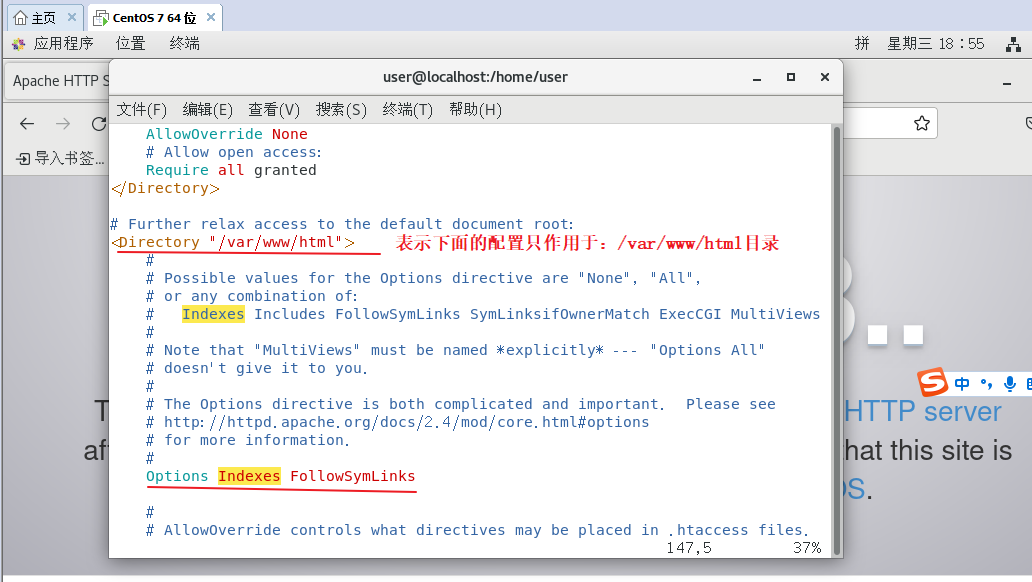
Apache访问控制
服务器相关的访问控制 Options指令 Options指令是Apache服务器配置文件中的一个重要指令,它可以用于控制特定目录启用哪些服务器特性。Options指令可以在Apache服务器的核心配置、虚拟主机配置、特定目录配置以及.htaccess文件中使用。 以下是一些常用的服务器特性选项: N…...

二、类与对象(二)
8 this指针 8.1 this指针的引入 我们先来定义一个日期的类Date: #include <iostream> using namespace std; class Date { public:void Init(int year, int month, int day){_year year;_month month;_day day;}void Print(){cout << _year <&l…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
