局部保持投影(Locality preserving projections,LPP)
局部保持投影(Locality preserving projections,LPP)
方法概述
核心思想
-
有映射 Y m ∗ n = f ( X d ∗ n ) \underset{m*n}{Y}=f(\underset {d*n}X) m∗nY=f(d∗nX),能够实现将d维的样本变换到m维空间之中
-
假设:对于一个好的降维方法,在高维空间下距离近(相似度高)的两个点,在低维空间下依旧保持相近的关系。高维空间相似度高的两个点在低维空间相似度依旧很高
-
考虑映射 Y = W T X Y=W^TX Y=WTX,即原样本空间中有 x i x_i xi与 x j x_j xj距离近, y i y_i yi 与 y j y_j yj( y i = W T x i y_i=W^T x_i yi=WTxi)仍保持相近关系
优化目标
- 定义优化目标:
m i n ∑ i ∑ j ∣ ∣ y i − y j ∣ ∣ 2 s i j min\sum_i \sum_j ||y_i - y_j||^2s_{ij} mini∑j∑∣∣yi−yj∣∣2sij
即在原始空间中近的点( s i j s_{ij} sij大),其在降维后应该尽可能接近( y i 与 y j 距离更小 y_i与y_j 距离更小 yi与yj距离更小)
方法推导:
- 对于LPP方法,有目标:
a r g m i n W ∑ i ∑ j ∣ ∣ y i − y j ∣ ∣ 2 s i j \underset{W}{arg\ min} \sum_i \sum_j ||y_i- y_j||^2s_{ij} Warg mini∑j∑∣∣yi−yj∣∣2sij
- 对于目标:
∑ i = 1 n ∑ j = 1 n ∣ ∣ y i − y j ∣ ∣ 2 s i j = ∑ i = 1 n ∑ j = 1 n ( y i T y i − y i T y j − y j T y i + y j T y j ) s i j = ∑ i = 1 n ( ∑ j = 1 n s i j ) 2 y i T y i − ∑ i = 1 n ∑ j = 1 n y i T y j s i j = 2 ∑ i n y i T y i d i i − 2 ∑ i n ∑ j n y i T y j s i j = 2 t r ( Y D Y T ) − 2 t r ( Y S Y T ) = 2 t r ( Y L Y T ) \sum_{i=1}^n \sum_{j=1}^n ||y_i- y_j||^2s_{ij}\\ =\sum_{i=1}^n \sum_{j=1}^n (y_i^Ty_i-y_i^Ty_j-y_j^Ty_i+y_j^Ty_j)s_{ij}\\ =\sum_{i=1}^n (\sum_{j=1}^ns_{ij})2y_i^Ty_i-\sum_{i=1}^n \sum_{j=1}^ny_i^Ty_js_{ij}\\ =2\sum_i^ny_i^Ty_id_{ii}-2\sum_i^n\sum_j^ny_i^Ty_js_{ij}\\ =2tr(YDY^T)-2tr(YSY^T)\\ =2tr(YLY^T)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=1∑nj=1∑n∣∣yi−yj∣∣2sij=i=1∑nj=1∑n(yiTyi−yiTyj−yjTyi+yjTyj)sij=i=1∑n(j=1∑nsij)2yiTyi−i=1∑nj=1∑nyiTyjsij=2i∑nyiTyidii−2i∑nj∑nyiTyjsij=2tr(YDYT)−2tr(YSYT)=2tr(YLYT)
去除乘数,最终优化目标为:
t r ( Y L Y T ) tr(YLY^T) tr(YLYT)
带入 Y = W T X Y = W^TX Y=WTX,得到最小化目标:
t r ( W T X L X T W ) tr(W^TXLX^TW) tr(WTXLXTW)
-
该目标存在平凡零解: W = O m ∗ d W=O_{m*d} W=Om∗d
此时L取最小值0,出现维度坍缩,所有样本映射到同一个点上,此解无意义
-
当W不取零矩阵时,由于没有添加尺度约束,在降维子空间一定(组成基向量方向一致)情况下,当尺度不断变小时,目标L会同时变小,无限趋于0,不存在最小值
-
因此,考虑对最小化目标变形为:
-
t r ( Y L Y T ) t r ( Y D Y T ) = t r ( W T X L X T W ) W T X D X T W \frac{tr(YLY^T)}{tr(YDY^T)} = \frac{tr(W^TXLX^TW)}{W^TXDX^TW} tr(YDYT)tr(YLYT)=WTXDXTWtr(WTXLXTW)
考虑到尺度因素,加以约束 Y D Y T = I YDY^T=I YDYT=I也即 W T X D X T W = I W^TXDX^TW=I WTXDXTW=I,
原始优化问题有多个解。由于是线性映射,若同比例缩小低维样本 y i y_i yi,得到的数据集Y都可作为最优的低维数据集。故加入约束: t r ( Y D Y ⊤ ) = ∑ i = 1 n d i i y i T y i = 1 tr(YDY^\top)=\sum_{i=1}^nd_{ii}y_i^Ty_i=1 tr(YDY⊤)=∑i=1ndiiyiTyi=1,通过限制 y i y_i yi的模长,使问题有唯一解。
-
-
参考LDA中提到的广义瑞利商,可知:
-
λ m i n ( ( X D X T ) − 1 ( X L X T ) ) ≤ t r ( W T X L X T W ) t r ( W T X D X T W ) ≤ λ m a x ( ( X D X T ) − 1 ( X L X T ) ) λ_{min}((XDX^T)^{-1}(XLX^T))≤\frac{tr(W^TXLX^TW)}{tr(W^TXDX^TW)}≤λ_{max}((XDX^T)^{-1}(XLX^T)) λmin((XDXT)−1(XLXT))≤tr(WTXDXTW)tr(WTXLXTW)≤λmax((XDXT)−1(XLXT))
变换矩阵: W = [ w 1 , w 2 , . . . , w m ] W=[w_1,w_2,...,w_m] W=[w1,w2,...,wm]由 ( X D X T ) − 1 ( X L X T ) (XDX^T)^{-1}(XLX^T) (XDXT)−1(XLXT)最小m个特征向量构成
-
-
矩阵形式推导:
由拉格朗日乘子法,构建L: L = t r ( W T X L X T W ) − t r ( Λ ( W T X D X T W − I ) ) L = tr(W^TXLX^TW)-tr(\Lambda(W^TXDX^TW-I)) L=tr(WTXLXTW)−tr(Λ(WTXDXTW−I))
对W求偏导并令为0:
2 X L X T W − 2 X D X T W Λ = 0 X L X T W = X D X T W Λ 有: ( X D X T ) − 1 X L X T W = W Λ 2XLX^TW-2XDX^TW\Lambda=0\\ XLX^TW= XDX^TW \Lambda\\ 有:(XDX^T)^{-1}XLX^TW=W\Lambda 2XLXTW−2XDXTWΛ=0XLXTW=XDXTWΛ有:(XDXT)−1XLXTW=WΛ
W由 ( X D X T ) − 1 X L X T (XDX^T)^{-1}XLX^T (XDXT)−1XLXT的特征向量作为列向量构成,且为了最小化目标函数,选取的特征向量应该是最小m个特征值对应的特征向量
相关定义
-
权重矩阵S:
-
定义样本 x i x_i xi和 x j x_j xj之间的权重 w i j w_{ij} wij, 原则是样本点之间距离越小,权重越大
-
权重矩阵S常用定义方式:
S i j = { s i j = e x p ( − ∣ ∣ x i − x j ∣ ∣ 2 t ) x i ∈ N k ( x j ) 即 x i 是 x j 的 k 近邻 s i j = 0 e l s e S_{ij} = \left\{ \begin{matrix} s_{ij} = exp(-\frac{||x_i - x_j||^2}{t})\ \ \ \ \ x_i∈N_k(x_j) 即x_i是x_j的k近邻\\ s_{ij}=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ else \end{matrix} \right. Sij={sij=exp(−t∣∣xi−xj∣∣2) xi∈Nk(xj)即xi是xj的k近邻sij=0 else
-
-
度矩阵D:
-
度矩阵D是一个对角阵,其对角元素 D i i = ∑ j = 1 n s i j D_{ii} = \sum_{j=1}^{n} s_{ij} Dii=∑j=1nsij
-
D = { ∑ j = 1 n s 1 j 0 . . . 0 0 ∑ j = 1 n s 2 j . . . 0 . . . . . . . . . . . . 0 0 . . . ∑ j = 1 n s n j } D= \left. \left \{ \begin{matrix} \sum_{j=1}^ns_{1j}\ \ \ \ 0\ \ \ \ ...\ \ \ \ 0 \\ 0\ \ \ \ \sum_{j=1}^ns_{2j}\ \ \ \ ...\ \ \ \ 0 \\ ...\ \ \ \ ...\ \ \ \ ...\ \ \ \ ... \\ 0\ \ \ \ 0\ \ \ \ ...\ \ \ \ \sum_{j=1}^ns_{nj} \end{matrix} \right. \right\} D=⎩ ⎨ ⎧∑j=1ns1j 0 ... 00 ∑j=1ns2j ... 0... ... ... ...0 0 ... ∑j=1nsnj⎭ ⎬ ⎫
-
-
拉普拉斯矩阵L:L=D-S
有运算:
Y D Y T = [ y 1 , y 2 , . . . , y n ] [ d 11 0 . . . 0 0 d 22 . . . 0 . . . . . . . . . . . . 0 0 . . . d n n ] [ y 1 T y 2 T . . . y n T ] = [ d 11 y 1 , d 22 y 2 , . . . , d n n y n ] [ y 1 T y 2 T . . . y n T ] = d 11 y 1 y 1 T + d 22 y 2 y 2 T + . . . + d n n y n y n T = ∑ i = 1 n y i d i i y i T = ∑ i = 1 n d i i y i y i T YDY^T = [y_1,y_2,...,y_n] \left. \left [ \begin{matrix} d_{11}\ \ \ \ 0\ \ \ \ ...\ \ \ \ 0 \\ 0\ \ \ \ d_{22}\ \ \ \ ...\ \ \ \ 0 \\ ...\ \ \ \ ...\ \ \ \ ...\ \ \ \ ... \\ 0\ \ \ \ 0\ \ \ \ ...\ \ \ \ d_{nn} \end{matrix} \right. \right] \left. \left [ \begin{matrix} y_1^T \\ y_2^T \\ ... \\ y_n^T \end{matrix} \right. \right] \\ =[d_{11}y_1,d_{22}y_2,...,d_{nn}y_n] \left. \left [ \begin{matrix} y_1^T \\ y_2^T \\ ... \\ y_n^T \end{matrix} \right. \right] \\ =d_{11}y_1y_1^T + d_{22}y_2y_2^T + ... + d_{nn}y_ny_n^T=\sum_{i=1}^ny_id_{ii}y_i^T=\sum_{i=1}^nd_{ii}y_iy_i^T\\ YDYT=[y1,y2,...,yn] d11 0 ... 00 d22 ... 0... ... ... ...0 0 ... dnn y1Ty2T...ynT =[d11y1,d22y2,...,dnnyn] y1Ty2T...ynT =d11y1y1T+d22y2y2T+...+dnnynynT=i=1∑nyidiiyiT=i=1∑ndiiyiyiT
因此有:
t r ( Y D Y T ) = ∑ i = 1 n d i i y i T y i tr(YDY^T) = \sum_{i=1}^nd_{ii}y_i^Ty_i tr(YDYT)=i=1∑ndiiyiTyi
类似可得:
t r ( Y S Y T ) = ∑ i = 1 n ∑ j = 1 n s i j y i T y j tr(YSY^T) = \sum_{i=1}^n\sum_{j=1}^ns_{ij}y_i^Ty_j tr(YSYT)=i=1∑nj=1∑nsijyiTyj
方法流程
1)由样本矩阵X构建权重矩阵S,度矩阵D,拉普拉斯矩阵L
2)求 ( X D X T ) − 1 X L X T (XDX^T)^{-1}XLX^T (XDXT)−1XLXT的特征向量,取最小m个作列向量构成变换矩阵W
3)由 Y = W T X Y=W^TX Y=WTX完成降维
相关文章:
)
局部保持投影(Locality preserving projections,LPP)
局部保持投影(Locality preserving projections,LPP) 方法概述 核心思想 有映射 Y m ∗ n f ( X d ∗ n ) \underset{m*n}{Y}f(\underset {d*n}X) m∗nYf(d∗nX),能够实现将d维的样本变换到m维空间之中 假设:对…...

Flutter:引领移动开发新潮流,跨平台应用程序的终极解决方案
文章目录 一、介绍二、环境搭建三、基础组件四、生命周期管理五、路由控制六、网络请求七、数据存储八、调试与优化《从零基础到精通Flutter开发》特色内容简介作者简介目录获取方式 一、介绍 Flutter是由Google开发的一款开源移动应用开发框架,它可以帮助开发者快…...
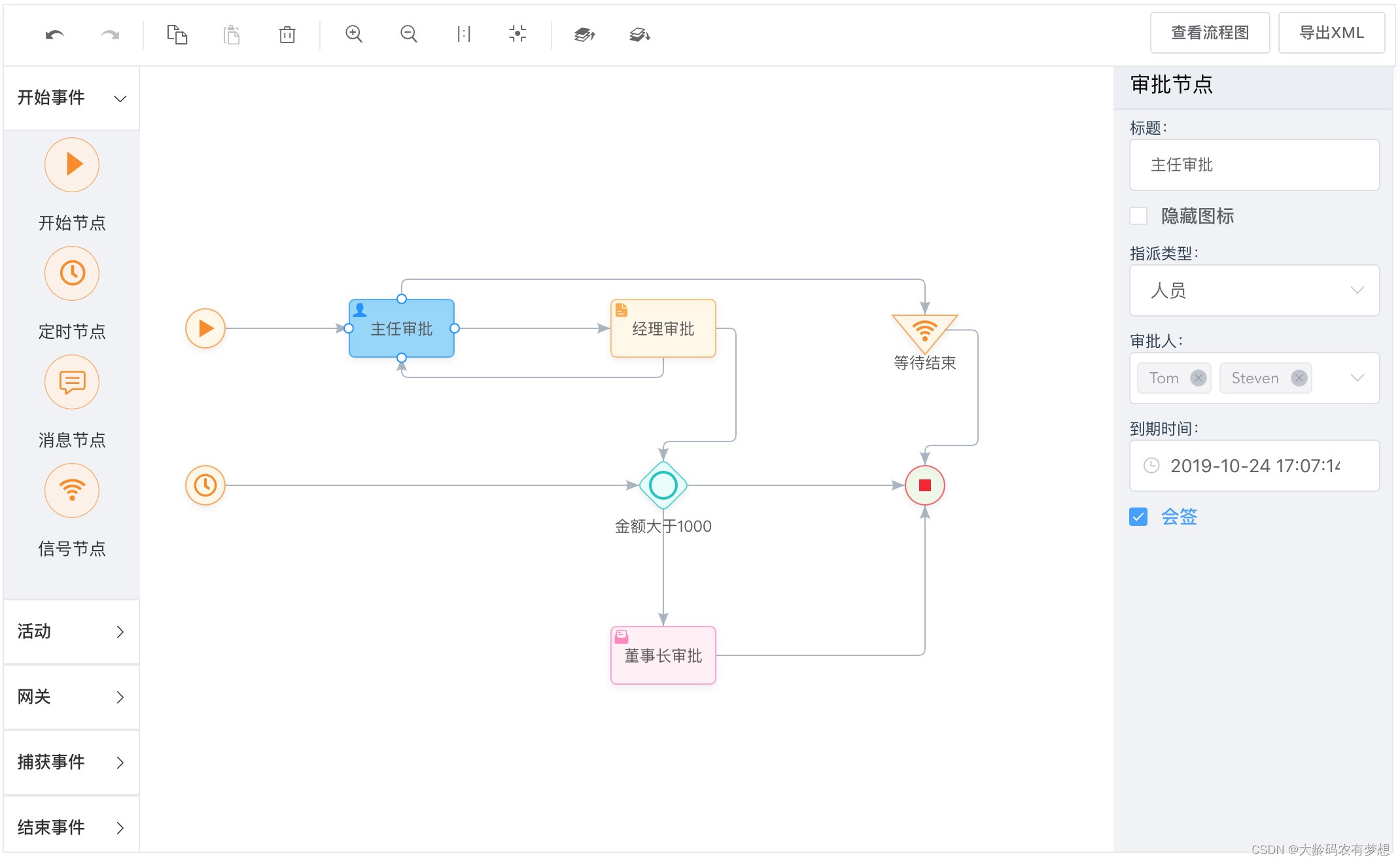
开源免费的流程设计器如何选型
大家在开发OA办公自动化、ERP、CRM、BPM、低代码平台等项目的时候,经常用到流程引擎,目前主流的开源流程引擎有activiti、flowable、camunda。这几个开源的流程引擎均基于BPMN2.0国际规范标准,其功能均比较强大,接口也很丰富。但涉…...

设置pdb自动启动
参考文档: How to Preserve Open Mode of PDBs When the CDB Restarts (Doc ID 1933511.1) -- 查看pdb的保留状态.无保留状态 select * from DBA_PDB_SAVED_STATES; SYScdbtest SQL> select * from DBA_PDB_SAVED_STATES;no rows selectedSYScdbtest SQL> -…...
抖店入驻成功后,新手需要怎么做?7天起店流程教会你!
我是电商珠珠 在抖店入驻成功后,很多新手并不知道怎么将抖店做起来。 我做抖店也已经3年时间了,期间也带着想做店的小伙伴一起,是第一波入驻抖店,并吃到抖店红利的商家。 虽然现在抖店起店比着去年、前年相对难了一些ÿ…...
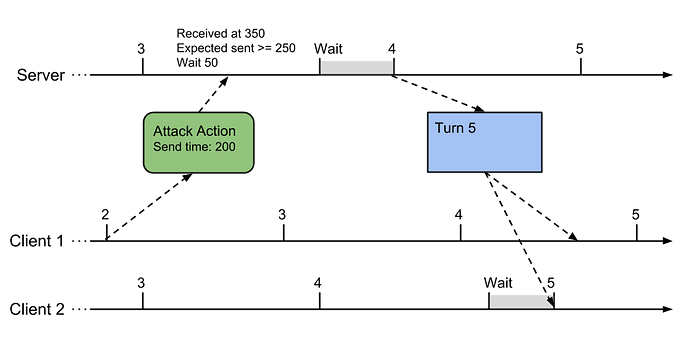
RTS 客户端-服务器网络
Stone Monarch 从一开始就支持多人游戏,但随着时间的推移,网络模型经历了多次迭代。我最初基于这篇著名的帝国时代文章实现了点对点锁步模型。 点对点锁定步骤有一些众所周知的问题。点对点方面使玩家很难相互连接,并增加了每个新玩家的网络…...

python连接数据库的方式
python连接数据库的方式 pyzenith.connect()函数就是连接数据库; exception.ScriptException()这一句是自定义异常,可以不用我这个; finally里面还有一个try finally是有必要的,防止…...

【腾讯云云上实验室-向量数据库】探索腾讯云向量数据库:全方位管理与高效利用多维向量数据的引领者
目录 前言1 腾讯云向量数据库介绍2 向量数据库信息及设置2.1 向量数据库实例信息2.2 实例监控2.3 密钥管理2.4 安全组2.5 Embedding2.6 可视化界面 3 可视化界面4 Embedding4.1 embedding_coll精确查询4.2 unenabled_embedding_coll精确查询 5 数据库5.1 创建数据库5.2 插入数据…...

二、sql手工注入
一、SQL注入的本质 解释:想要进行sql注入,肯定要发现注入点,一般简单的sql注入通过下面两种方式判断就能发现是否存在sql注入漏洞 1.字符型 注意:字符型注入可能为或" 查询语句: select * from student where…...

day61 layui和分页原理
昨日内容回顾 choices参数的使用 一般用在什么场景:当被存储的字段数据可能被列举完毕的时候一般会使用choices参数 性别 学历 来源 工作经验等 一般情况下不在数据表中直接存储中文,存数字、存字母来做映射 # 怎么使用 gender_choices ((1, 男),(2…...

Rust开发——变量、静态变量与常量
1.变量 在 Rust 中,类型安全是通过静态类型系统来实现的。变量绑定默认情况下是不可变的(immutable)。 在 Rust 中声明一个变量时,默认情况下它是不可变的。例如: fn main() {let x :i32 5; // 这是一个…...

javascript Math相关计算取值属性方法
*向上取整【只要有小数就+1】 Math.ceil(3.14); // 4 *向下取整【有小数就舍弃】 Math.floor(3.14); // 3 parseInt(3.14); // 3 // 常用于字符串类型的数字转为十进制的数据 四舍五入【小数点后部分】 Math.round(11.5)); //12 Math.round(-11.5)); //-11 取两数…...

git reset hard,mixed,soft
首先,我们得了解git reset命令的形式之一: git reset [<mode>] [<commit>] 此命令的作用是恢复HEAD分支到<commit>位置,并根据<mode>决定是否恢复index file和working tree。恢复是指将staging area和working tree…...

Cookie与Session知识
目录 一.Cookie与Session的发展史 1.Cookie的发展史 2.Session的发展史 3.Cookie和Session的关系 4.总结 二.Cookie与Session详解 1.Cookie 2.Session 3.token 4.总结 三.Django操作Cookie 1.设置Cookie 2.获取Cookie 3.设置超时时间 4.注销Cookie 5.登录功能实…...
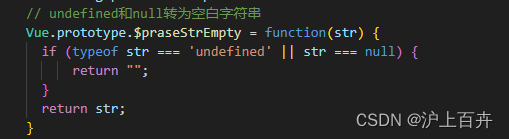
Vue批量全局处理undefined和null转为““ 空字符串
我们在处理后台返回的信息,有的时候返回的是undefined或者null,这种字符串容易引起用户的误解,所以需要我们把这些字符串处理一下。 如果每个页面都单独处理,那么页面会很冗余,并且后期如果有修改容易遗漏,…...
【2023年APMCM亚太杯C题】完整数据与解题思路
2023年亚太杯C题 数据下载与搜集重点数据其余数据第一问第二问第三问第四问第五问第六问 数据与思路获取 数据下载与搜集 该题并没有提供数据集,对所需数据进行收集整理是对题目进行求解的基础。在本题中,主要需要以下数据:新能源汽车历史销…...
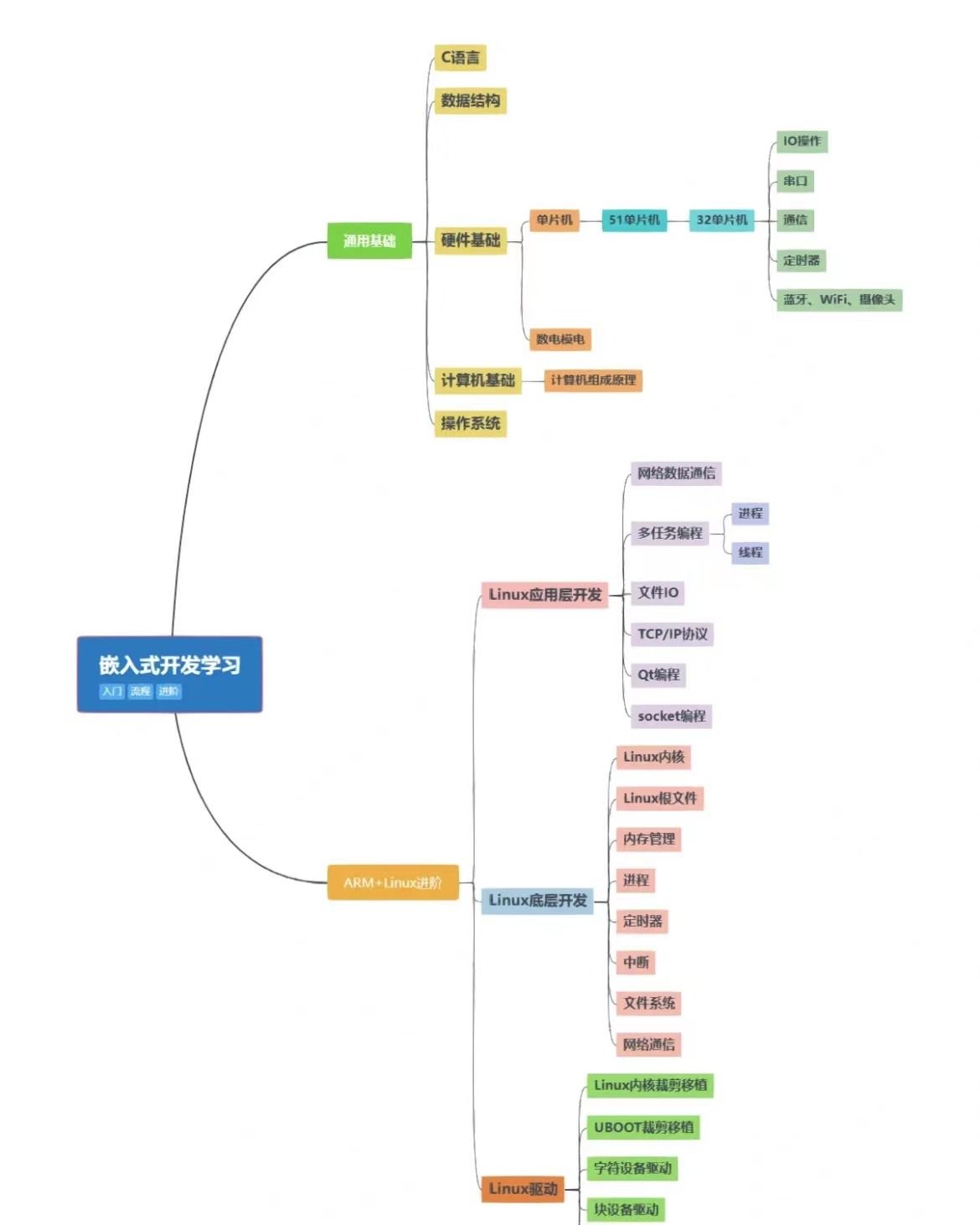
嵌入式单片机方向和Linux驱动开发方向哪个发展前景好?
嵌入式单片机方向和Linux驱动开发方向哪个发展前景好? 在某些平台上看到很多人鼓吹嵌入式Linux开发比单片机开发要好,让所有人都去做嵌入式Linux开发。说这种话的人大多数是嵌入式Linux的培训机构,或者是一开始就以嵌入式Linux入门的那一批人…...
如何搭建Zblog网站并通过内网穿透将个人博客发布到公网
文章目录 1. 前言2. Z-blog网站搭建2.1 XAMPP环境设置2.2 Z-blog安装2.3 Z-blog网页测试2.4 Cpolar安装和注册 3. 本地网页发布3.1. Cpolar云端设置3.2 Cpolar本地设置 4. 公网访问测试5. 结语 1. 前言 想要成为一个合格的技术宅或程序员,自己搭建网站制作网页是绕…...
)
2:kotlin集合(Collections)
集合有助于数据分组,方便后续操作 集合类型说明Lists有序的可重复的集合Sets无序的不可重复的集合Maps键值对映射集合,键唯一,且一个键只能映射到一个值 每个集合类型都可以是可变的或者只读的 List List按照添加的顺序存储内容ÿ…...
小诺2.0开源版工程启动
小诺是一款开源的前后端开发框架,同若依、SpringBladex一样可作为私活、外包脚手架。 开源地址:Snowy: 最新:💖国内首个国密前后分离快速开发平台💖,采用Vue3AntDesignVue3 ViteSpringBootMpHuToolSaToke…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
