容斥 C. Strange Function改编题
补题:
题目详情 - 9.段坤爱取模%%% - SUSTOJ
本题或许是参考 Problem - C - Codeforces
根据题意,f(i)就是不能被整除的最小的一个质因子。
打表发现,当15个质因子相乘后,长度就大于18。

因此可以知道小于等于1e16内的正整数x,f(x)一定是前20个质因子之一,且合数一定不行。
前20个质因子:2 3 5 7 11 13 17 19 23 29 31 37 41 43 。在第15个质因子相乘时就大于1e16,因此max(f(i))是小于40的。
现在就是要求:第1个质因子在[l, r]的个数 乘上 第1个质因子,加上 第2个质因子在[l, r]的个数 乘上 第2个质因子个数, … 。需要保证i在[l, r]内仅且一次被计算。考虑容斥。
对于f(i) = k来说,i可以被1 ... k - 1任何一个整除,但是不能被k整除。
f()值为k的个数有:
⌊ r l c m ( 1 , . . . k − 1 ) − r l c m ( 1 , . . . k ) ⌋ − ⌊ l l c m ( 1 , . . . k − 1 ) − l l c m ( 1 , . . . k ) ⌋ \lfloor { \frac {r} {lcm(1, ... k-1)} } - { \frac {r} {lcm(1, ... k)} } \rfloor - \lfloor { \frac {l} {lcm(1, ... k-1)} } - { \frac {l} {lcm(1, ... k)} } \rfloor ⌊lcm(1,...k−1)r−lcm(1,...k)r⌋−⌊lcm(1,...k−1)l−lcm(1,...k)l⌋
如果将[l, r]分成两部分[1, l]和[1, r]来处理的话。
以r为例,f()为k的个数:
⌊ r l c m ( 1 , . . . k − 1 ) − r l c m ( 1 , . . . k ) ⌋ \lfloor { \frac {r} {lcm(1, ... k-1)} } - { \frac {r} {lcm(1, ... k)} } \rfloor ⌊lcm(1,...k−1)r−lcm(1,...k)r⌋
那么,[1, r]内sum就是:
∑ k ≥ 2 k × ( ⌊ r l c m ( 1 , . . . k − 1 ) − r l c m ( 1 , . . . k ) ⌋ ) = 2 × ( r − ⌊ r l c m ( 1 , 2 ) ⌋ ) + 3 × ( ⌊ r l c m ( 1 , 2 ) − r l c m ( 1 , 2 , 3 ) ⌋ ) + . . . = r + ∑ k ≥ 1 ⌊ r l c m ( 1 , . . . , k ) ⌋ \sum_{k \ge 2}k \times(\lfloor { \frac {r} {lcm(1, ... k-1)} } - { \frac {r} {lcm(1, ... k)} } \rfloor) \\ = 2 \times (r - \lfloor \frac r {lcm(1,2)} \rfloor) + 3 \times (\lfloor { \frac {r} {lcm(1,2)} } - { \frac {r} {lcm(1,2,3)} } \rfloor) + ... \\ = r + \sum_{k \ge 1} \lfloor \frac r {lcm(1, ..., k)} \rfloor k≥2∑k×(⌊lcm(1,...k−1)r−lcm(1,...k)r⌋)=2×(r−⌊lcm(1,2)r⌋)+3×(⌊lcm(1,2)r−lcm(1,2,3)r⌋)+...=r+k≥1∑⌊lcm(1,...,k)r⌋
同理,可得[1, l]内的sum,两者相减即为答案。对于cf上的C,[1, r]即可。
时间复杂度:前面稠密,后面稀疏,最大为O(41 * 2)。
const int mod = 998244353;
// https://codeforces.com/contest/1542/problem/C
void solve() {int l,r; cin>>l>>r;int sum = 0;int v = 1;auto lcm = [&](int a, int b) {return a * b / __gcd(a,b);};for(int i = 1; v <= r; v = lcm(i, v), ++i) {sum = (sum + r / v) % mod;}v = 1;for(int i = 1; v <= l - 1; v = lcm(i,v), ++i) {sum = (sum - (l - 1) / v + mod) % mod;}cout<<sum<<endl;
}
总结
赛时对这题容斥没有找到切入点。这个容斥处理极具有思维性,还是需要多做思维题!
参考:
[Codeforces] number theory (R1600) Part.11 - 知乎 (zhihu.com)
Submission #121200660 - Codeforces
相关文章:

容斥 C. Strange Function改编题
补题: 题目详情 - 9.段坤爱取模%%% - SUSTOJ 本题或许是参考 Problem - C - Codeforces 根据题意,f(i)就是不能被整除的最小的一个质因子。 打表发现,当15个质因子相乘后,长度就大于18。 因此可以知道小于等于1e16内的正整数x…...

C++笔记
文章目录 类模板类函数什么是友元函数?什么是内联函数?VECTOR哈希表栈队列映射与解除映射mmap()munmap可变参数 va_start()-va_send()vsnprintf()C/C++异常处理list红黑树类 基类、父类、顶层类、抽象类 子类、派生类 模板类 在C++中,模板类(Template Class)是一种通用…...
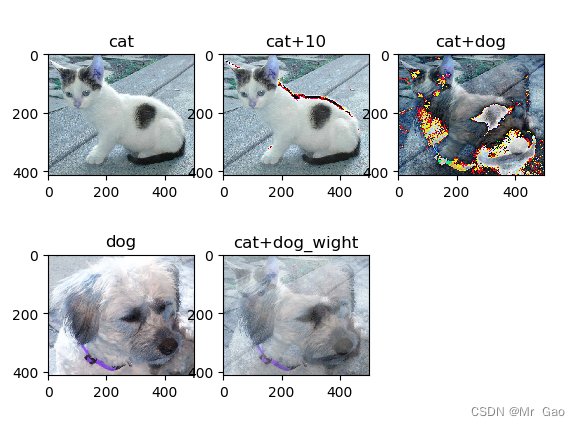
python-opencv 培训课程笔记(1)
python-opencv 培训课程笔记(1) 博主参加了一次opencv库的培训课程,把课程所学整理成笔记,供大家学习,第一次课程包括如下内容: 1.读取图像 2.保存图像 3.使用opencv库显示图像 4.读取图像为灰度图像 …...
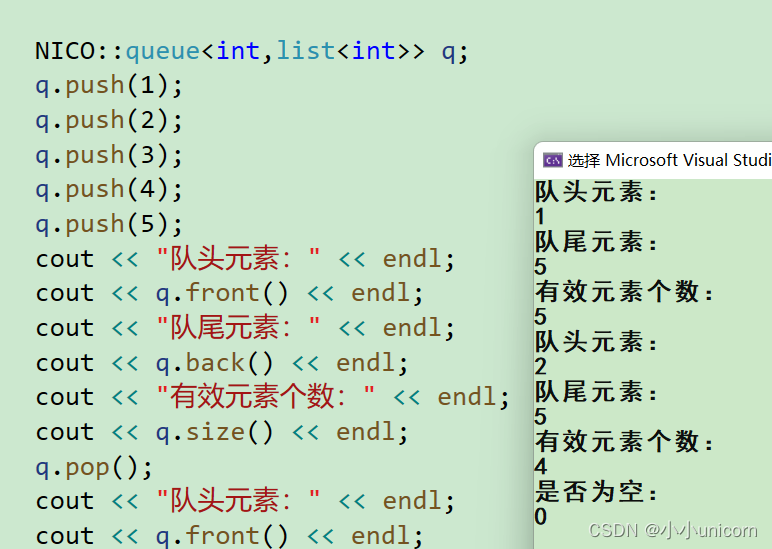
【C++初阶】STL详解(七)Stack与Queue的模拟实现
本专栏内容为:C学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚代码仓库:小小unicorn的代码仓库&…...

校园报修抢修小程序系统开发 物业小区报修预约上门维修工单系统
开发的功能模块有: 1.报修工单提交:学生、教职员工等可以使用小程序提交报修请求。这通常包括选择报修的问题类型(如水漏、电器故障、照明问题等),地点,报修联系人,联系电话等,并提供…...

【Android】Hilt比Android好在哪里
Hilt框架的功能和设计理念,和Dagger基本是完全一致的,Hilt也是完全在Dagger基础上进行开发的 但是Dagger的用法比较繁琐,Hilt主要是做了便用性上的改进,主要有以下点 提供常用Component,不用再为每个InjectTarget都创…...
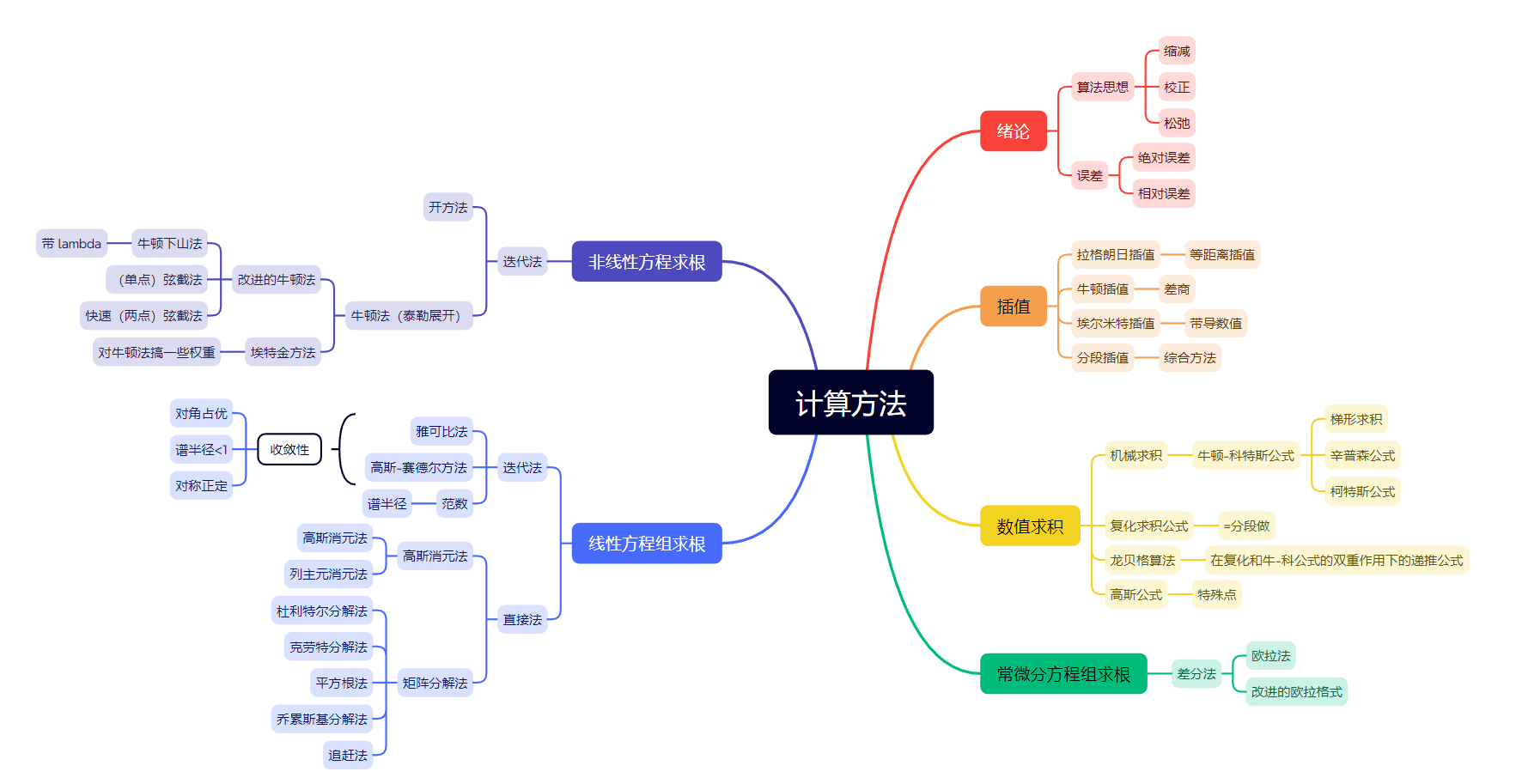
计算方法 期末总结
思维导图 绪论 算法的性质: 有穷性、确切性、有输入输出、可行性 算法的描述方法: 自然语言、伪代码、流程图、N-S流程图 算法设计思想: 化大为小的缩减技术:二分法化难为易的校正技术:开方法化粗为精的松弛技术&a…...

【面试】jvm中堆是分配对象存储的唯一选择吗
目录 一、说明二、逃逸分析2.1 说明2.2 参数设置 一、说明 1.在《深入理解Java虚拟机》中关于Java堆内存有这样一段描述:随着JIT编译期的发展与逃逸分析技术逐渐成熟,栈上分配、标量替换优化技术将会导致一些微妙的变化,所有的对象都分配到堆上也渐渐变得…...

音视频同步笔记 - 以音频时间为基
音视频同步 - 以音频时间为基 上图介绍: 该图是以音频的时间为基,对视频播放时间的延迟控制方案,只调整视频的播放延时。delayTime是视频播放的延迟时间,初始值是1 / FPS * 1000 (ms),如果FPS为25帧率,初始…...
之间的关系)
JavaScript 原始数据类型和对应的对象类型(内置对象)之间的关系
JavaScript 原始数据类型和对应的对象类型(内置对象)之间的关系 JavaScript 的原始(primitive)数据类型包括包括数字(Number)、字符串(String)、布尔值(Boolean…...

报错For debugging consider passing CUDA_LAUNCH_BLOCKING=1.
.报错For debugging consider passing CUDA_LAUNCH_BLOCKING1. /aten/src/ATen/native/cuda/NLLLoss2d.cu:103: nll_loss2d_forward_kernel: block: [29,0,0], thread: [707,0,0] Assertion t > 0 && t < n_classes failed. 报错信息如下: ./aten/…...
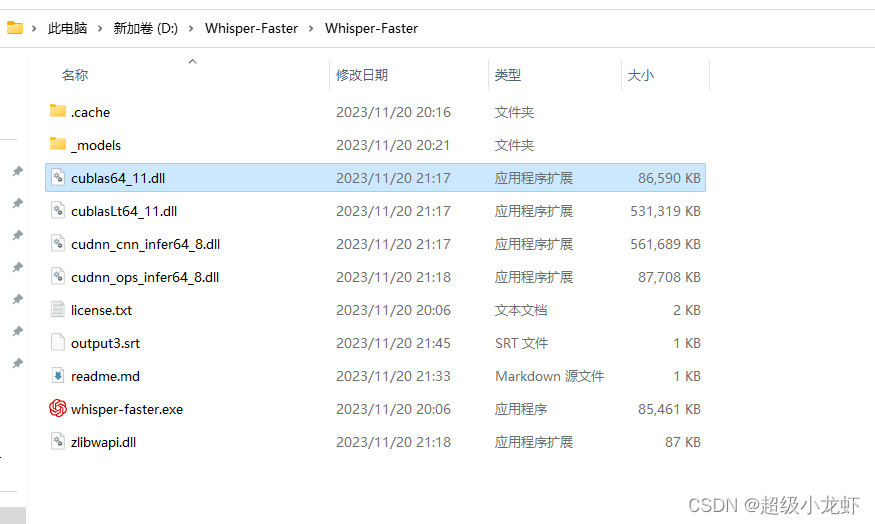
whisper使用方法
看这个 github https://github.com/Purfview/whisper-standalone-win/tags下载 视频提取音频 ffmpeg -i 222.mp4 -vn -b:a 128k -c:a mp3 output.mp3截取4秒后的音频 ffmpeg -i output.mp3 -ss 4 -c copy output2.mp3使用 whisper-faster.exe 生成字幕 whisper-faster.exe …...

通过easyexcel实现数据导入功能
上一篇文章通过easyexcel导出数据到excel表格已经实现了简单的数据导出功能,这篇文章也介绍一下怎么通过easyexcel从excel表格中导入数据。 目录 一、前端代码 index.html index.js 二、后端代码 controller service SongServiceImpl 三、功能预览 四、后端…...

Springboot_文件下载功能(前端后端)
遇到的问题: 文件下载后文件一直被破坏,无法正常打开文件名乱码,如图 刚开始一直在纠结,是不是后端没有写对,然后导致下载不能使用 后来搜索了一些资料,发现后端没什么问题 然后就开始找到其他项目对比…...
Vue框架学习笔记——v-bind数据单向绑定和v-model数据双向绑定
文章目录 v-bind,数据单向绑定简写形态(省略v-bind,只留冒号)示例一(将输入框数据改为:哈哈哈哈哈):实例二(将Vue实例中的name改为字符串:"单向绑定&quo…...

将对象转成URL参数
背景 有的时候前端跳转到其他平台的页面需要携带额外的参数,需要将对象转成用 & 连接的字符串拼接在路径后面。 实现方法...

【论文阅读】MAG:一种用于航天器遥测数据中有效异常检测的新方法
文章目录 摘要1 引言2 问题描述3 拟议框架4 所提出方法的细节A.数据预处理B.变量相关分析C.MAG模型D.异常分数 5 实验A.数据集和性能指标B.实验设置与平台C.结果和比较 6 结论 摘要 异常检测是保证航天器稳定性的关键。在航天器运行过程中,传感器和控制器产生大量周…...
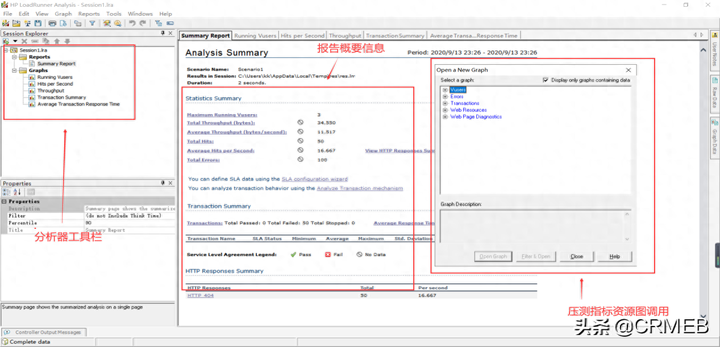
超级武器!深入LoadRunner性能测试流程及极速分析结果!
性能测试目的 1 什么是性能测试? 性能测试是通过性能的测试工具模拟多种正常、峰值以及异常负载条件来对系统的各项性能指标进行测试。 负载测试和压力测试都属于性能测试,两者可以结合进行。通过负载测试,确定在各种工作负载下系统的性能࿰…...

解决requests库进行爬虫ip请求时遇到的错误的方法
目录 一、超时错误 二、连接错误 三、拒绝服务错误 四、内容编码错误 五、HTTP错误 在利用requests库进行网络爬虫的IP请求时,我们可能会遇到各种错误,如超时、连接错误、拒绝服务等等。这些错误通常是由目标网站的限制、网络问题或我们的爬虫代码中…...

大语言模型领域的重要术语解释
前言 本人对人工智能非常感兴趣,目前是一名初学者,在研究大语言模型的一些内容。很多模型都是用英文提出的,其中也包括很多概念,有些概念的中文翻译和其想表达的意思不完全一样,所以在这里,想更加精准地帮…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
