bug场景记录
项目场景:
mapper.xml文件中sql语句执行失败,显示输入的参数数量不对
问题描述
<select id="page" resultType="com.sky.entity.Employee">select * from employee<where><if test="name != null and name !=''">and name like concat('%','#{name}','%')</if></where>order by create_time desc</select>
xml文件出错
原因分析:
当name的输入为中文字符串时,例如 “标准" 二字会导致mybatis无法自动注入name
解决方案:
将xml文件中的sql语句修改为
<select id="page" resultType="com.sky.entity.Employee">select * from employee<where><if test="name != null and name !=''">and name like concat('%',#{name},'%')</if></where>order by create_time desc</select>
去掉单引号即可
相关文章:

bug场景记录
项目场景: mapper.xml文件中sql语句执行失败,显示输入的参数数量不对 问题描述 <select id"page" resultType"com.sky.entity.Employee">select * from employee<where><if test"name ! null and name !"…...

【云备份】第三方库的认识与使用
文章目录 json库粗略认识详细认识writer 类reader类jsoncpp序列化实现jsoncpp反序列化实现 bundle文件压缩库简单认识bundle库实现文件压缩bundle库实现文件解压缩 httplib库Request类Response类Server类Client类 json库 粗略认识 json是一种数据交换格式,采用完全…...

6.2.SDP协议
那今天呢?我们来介绍一下sdp协议,那实际上呢?sdp协议非常的简单。我们如果拿到一个stp的文档去看的话,那你要分阅里边的所有的内容会觉得很枯燥,但实际上呢,如果我们按照这张图所展示的结构去看stp的话。你…...

[汇编实操]DOSBox工具安装——Ubuntu18.04系统
一、下载&安装 sudo apt install -y dosbox 二、启动 dosbox 三、C盘挂载 将上述文件下载放在任意路径,将DEBUG目录映射为虚拟C盘 MASM.EXE 是用来编译的,LINK.EXE 用来链接,这俩是必须的。 执行如下命令: mount c /m…...

前端 HTML 的 DOM 事件相关知识有哪些?
HTML 的 DOM 事件是指在网页上发生的各种事件,如点击、鼠标移动、键盘输入等。 通过 JavaScript 脚本可以对这些事件进行监听和处理,以实现交互效果。以下是一些常见的 DOM 事件及其相关知识点: 1、click:点击事件,在…...
Mac自带的看图如何连续查看多张图片
一、问题 mac看访达里的图片时,双击打开一张图片,然后按上下左右键都没法切换到另外的图片。而且也没找到像window一样单击缩略图可以看到预览图。其实是自己不懂得怎么使用,哈哈哈😂 二、方法 2.1、图标方式 可以看到缩略图&a…...
HTTP四大参数类型及请求参数的方式和如何接收
HTTP 请求中4大参数类型和接收方法。 1、请求头参数head 请求头参数顾名思义,是存放在请求头中发送给服务器的参数,服务器通过解析请求头获取参数内容。通常会存放本次请求的基本设置,以帮助服务器理解并解析本次请求的body体。 参数形式如…...

【C++11】default、delete与Noncopyable
C11 oop中的default、delete与Noncopyable default 在C11标准中,可以使用default关键字来显式地声明默认的构造函数和析构函数。 使用default关键字可以用来显式声明默认的构造函数和析构函数。这样做可以让编译器自动生成默认实现 –>->->关于构造函数…...
【心得】基于flask的SSTI个人笔记
目录 计算PIN码 例题1 SSTI的引用链 例题2 SSTI利用条件: 渲染字符串可控,也就说模板的内容可控 我们通过模板 语法 {{ xxx }}相当于变相的执行了服务器上的python代码 利用render_template_string函数参数可控,或者部分可控 render_…...

ubuntu20.04 nginx 部署静态网页
1、安装nginx Ubuntu环境下安装部署Nginx(有网)_ubuntu 安装nginx_荒Huang的博客-CSDN博客 2、压缩并上传文件到服务器指定位置(unzip命令),修改nginx配置文件,指定root目录为文件的目录,index 值为指定的html文件 …...

vue脚手架的基础搭建过程
MVVM架构 Vue框架底层设计遵循MVVM架构。 Model层(M)模型层(业务逻辑层) View层(V)视图层 主管UI ViewModel层(VM) 将项目代码划分清晰的层次结构后,非常有利于后期代…...

函数与数组
一.函数 1、函数的作用 定义较为复杂的但是需要重复使用的内容,以便再次使用,可以直接调用,节约时间,提高效率。 语句块定义成函数约等于别名,定义函数,再引用函数。 封装的可重复利用的具有特定功能的…...

2023年【安全生产监管人员】考试题及安全生产监管人员找解析
题库来源:安全生产模拟考试一点通公众号小程序 安全生产监管人员考试题参考答案及安全生产监管人员考试试题解析是安全生产模拟考试一点通题库老师及安全生产监管人员操作证已考过的学员汇总,相对有效帮助安全生产监管人员找解析学员顺利通过考试。 1、…...
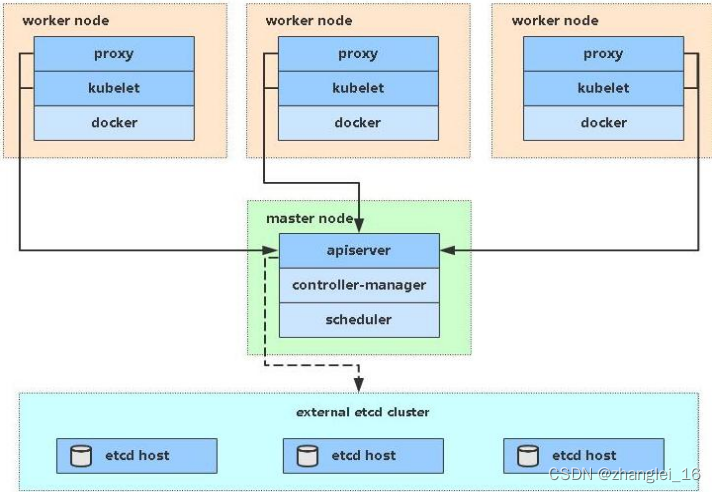
K8S(一)
一、kubernetes 概述 1、kubernetes 基本介绍 kubernetes,简称 K8s,是用 8 代替 8 个字符“ubernete”而成的缩写。是一个开源的,用于管理云平台中多个主机上的容器化的应用,Kubernetes 的目标是让部署容器化的 应用简单并且高效…...
Linux快速显示文件行号并跳转
有时候,想要在线上直接查看日志文件,搜索到关键词后,如果一直按n找下去,很麻烦,我们可以先显示出行号,确定好我们要找内容对应的行号,直接跳转过去。 esc进入命令模式,输入:set nu命…...
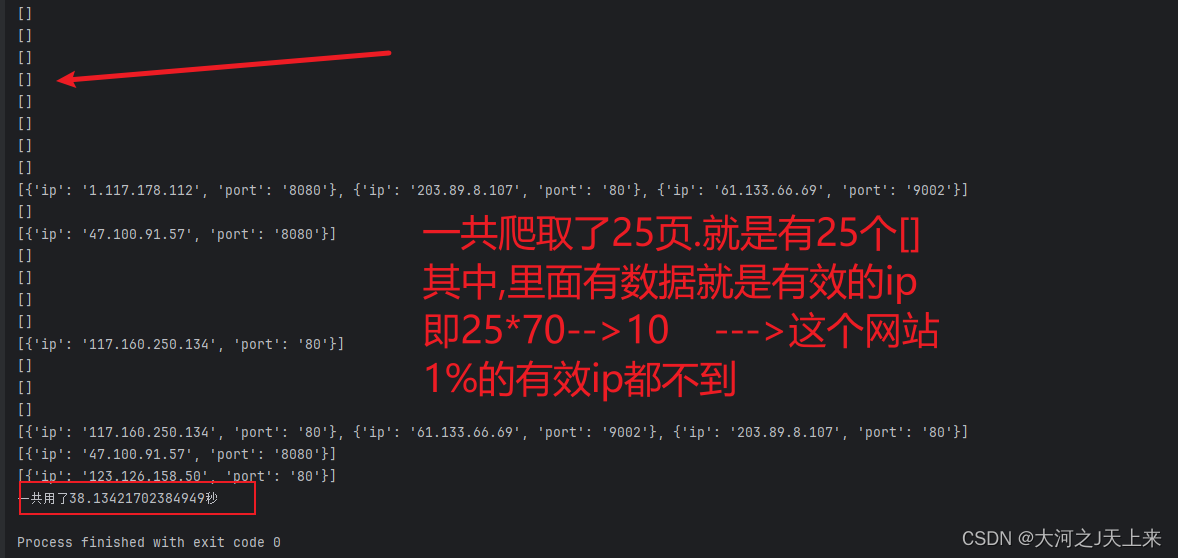
异步爬取+多线程+redis构建一个运转丝滑且免费http-ip代理池 (二)
继上一章: CSDN 本次需要做的是进行有效ip的验证! 我们知道,从网页上爬取上千上万个ip之后,因为是免费的代理,所以,对这上千上万个ip进行验证有效性就需要考虑效率上的问题了; 而验证ip有效性的唯一办法,就是通过对网络发起请求;如果state200,就是有效,否则就是无效; 而上…...

HugeGraph安装与使用
1、HugeGraph-Server与HugeGraph-Hubble下载 HugeGraph官方地址:https://hugegraph.apache.org/ 环境为:linux 官网是有模块版本对应关系,尽量下载较新版本,hubble1.5.0之前是studio功能比较少。官网已经下架server,其他模块下载也比较慢。可以在网上找…...

计算机端口
前言 计算机端口(Port)是一种用于在计算机网络中标识特定服务或应用程序的机制。 端口是一个数字,范围从0到65535,用于将网络通信分配给不同的应用程序或服务。 在 Internet 协议套件(TCP/IP)中࿰…...
激发创新,助力研究:CogVLM,强大且开源的视觉语言模型亮相
项目设计集合(人工智能方向):助力新人快速实战掌握技能、自主完成项目设计升级,提升自身的硬实力(不仅限NLP、知识图谱、计算机视觉等领域):汇总有意义的项目设计集合,助力新人快速实…...

centos 6.10 安装 perl 5.14
下载安装包 运行下面命令: wget http://www.cpan.org/src/5.0/perl-5.14.2.tar.gz也可以直接下载好安装包,再拷到虚拟机 安装 执行下面命令 tar -xvzf perl-5.14.2.tar.gz #解压安装包 cd perl-5.14.2 ./Configure -des -Dprefix/usr/local/perl ma…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
