数据结构与算法【B树】的Java实现+图解
目录
B树
特性
实现
节点准备
大体框架
实现分裂
实现新增
实现删除
完整代码
B树
也是一种自平衡的树形数据结构,主要用于管理磁盘上的数据管理(减少磁盘IO次数)。而之前说的AVL树与红黑树适合用于内存数据管理。存储一个100w的数据使用AVL存储,树高大约为20层(),如果使用磁盘IO查询20次效率较低。
特性
度degree:指树中节点孩子数
阶order:指所有节点孩子数中最大值
一棵 B-树具有以下性质
特性1:每个节点 x 具有
- 属性 n,表示节点 x 中 key 的个数
- 属性 leaf,表示节点是否是叶子节点
- 节点 key 可以有多个,以升序存储
特性2:每个节点最多具有m个孩子,其中m叫做B-树的阶
特性3:除根结点与叶子节点外,每个节点至少有ceil(m/2)个孩子,根节点不是叶子节点时,最少有两个孩子。叶子节点没有孩子
特性2:每个非叶子节点中的孩子数是 n + 1。而n的取值为ceil(m/2)-1<=n<=m-1。
特性3:最小度数t(节点的孩子数称为度)和节点中键数量的关系如下:
| 最小度数t | 键数量范围 |
|---|---|
| 2 | 1 ~ 3 |
| 3 | 2 ~ 5 |
| 4 | 3 ~ 7 |
| ... | ... |
| n | (n-1) ~ (2n-1) |
其中,当节点中键数量达到其最大值时,即 3、5、7 ... 2n-1,需要分裂
特性4:叶子节点的深度都相同
实现
节点准备
B树的节点属性,与其他树不太相同,首先是key可以有多个,因此要设置为数组,孩子节点也未知,因此也要设置为数组。本应该还存在一个value属性,这里简化掉,不添加该属性。
static class Node {boolean leaf = true; //是否是叶子节点int keyNumber; //有效keyint t; //最小度int[] keys; // keys数组Node[] children; //孩子节点数组public Node(int t) {this.t = t;this.keys = new int[2 * t - 1];this.children = new Node[2 * t];//最大孩子节点个数为为2*t}@Overridepublic String toString() {return Arrays.toString(Arrays.copyOfRange(keys, 0, keyNumber));}/*** 根据key获取对应节点** @param key* @return*/Node get(int key) {int i = 0;while (i < keyNumber) {//如果在该节点找到,那么直接返回即可if (keys[i] == key) {return this;}//说明要找的元素可能在children[i]中if (keys[i] > key) {break;}i++;}//如果是叶子节点,直接返回nullif (leaf) {return null;}return children[i].get(key);}/*** 指定位置插入元素** @param key* @param index*/void insertKey(int key, int index) {System.arraycopy(keys, index, keys, index + 1, keyNumber - index);keys[index] = key;keyNumber++;}/*** 向节点中插入孩子节点* @param child* @param index*/void insertChild(Node child, int index) {System.arraycopy(children, index, children, index + 1, keyNumber - index);children[index] = child;}
}这里我采用了静态数组,因此需要多添加一个keyNumber参数来获取有效key的数量,如果使用ArrayList,可以通过size方法获取,因此不需要添加这个属性。
大体框架
public class BTree {private Node root;private int t;//最小度数final int MAX_KEY_NUMBER;//最大key数量final int MIN_KEY_NUMBER;//最小key数量。用于分裂使用public BTree(int t) {this.t = t;root = new Node(t);MAX_KEY_NUMBER = 2 * t - 1;MIN_KEY_NUMBER = 2 * t;}static class Node {boolean leaf = true; //是否是叶子节点int keyNumber; //有效keyint t; //最小度int[] keys; // keys数组Node[] children; //孩子节点数组public Node(int t) {this.t = t;this.keys = new int[2 * t - 1];this.children = new Node[2 * t];//最大孩子节点个数为为2*t}@Overridepublic String toString() {return Arrays.toString(Arrays.copyOfRange(keys, 0, keyNumber));}/*** 根据key获取对应节点** @param key* @return*/Node get(int key) {int i = 0;while (i < keyNumber) {//如果在该节点找到,那么直接返回即可if (keys[i] == key) {return this;}//说明要找的元素可能在children[i]中if (keys[i] > key) {break;}i++;}//如果是叶子节点,直接返回nullif (leaf) {return null;}return children[i].get(key);}/*** 指定位置插入元素** @param key* @param index*/void insertKey(int key, int index) {System.arraycopy(keys, index, keys, index + 1, keyNumber - index);keys[index] = key;keyNumber++;}/*** 向节点中插入孩子节点** @param child* @param index*/void insertChild(Node child, int index) {System.arraycopy(children, index, children, index + 1, keyNumber - index);children[index] = child;}}
}实现分裂
先说分裂规律,当新增一个节点后使节点中的key满足2t-1,那么该节点就会被分裂。
- 创建一个新的节点,暂时称为right节点(分裂后会在被分裂节点的右边)
- 被分裂节点把 t 以后的 key 和 child 都拷贝到right节点
- t-1 处的 key 插入到 parent 的 index 处,index 指被分裂节点作为孩子时的索引
- right 节点作为 parent 的孩子插入到 index + 1 处
图示如下:
红色部分的意思是当前节点是父结点中作为孩子的下标。黑色部分是key,小数字代表key的下标。
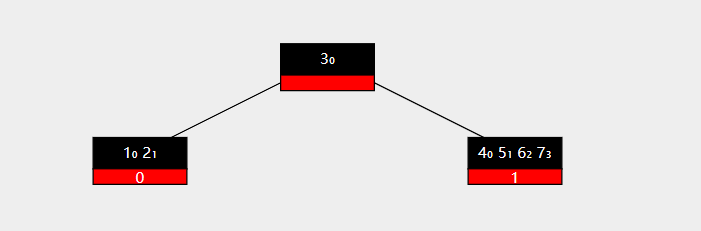
起始存在一个t为3的B树。那么最大key就为 2*3-1 。此时作为父结点孩子下标为1的节点以及存在 4 个key,再添加一个key就会触发分裂。
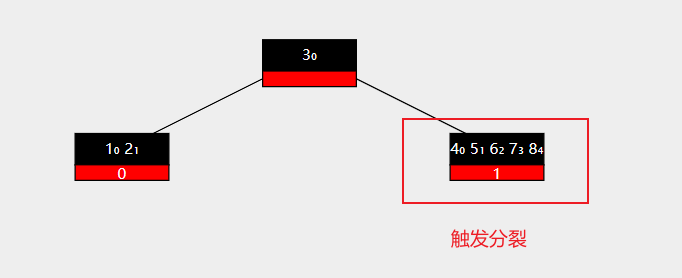
现在,再添加一个新的key值 8 ,此时到达最大key数,触发分裂



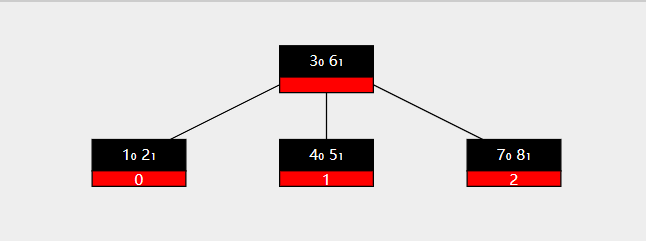
此时分裂结束,分裂后结果如下
具体实现代码如下
private void split(Node parent, int index, Node split) {if (parent == null) {//说明分割根节点,除了需要创建right节点之外,还需要创建parent节点parent = new Node(t);parent.leaf = false;parent.insertChild(split, 0);root = parent;}Node right = new Node(t);//将被分裂节点的一部分key放入right节点中。System.arraycopy(split.keys, index, right.keys, 0, t - 1);//新建的节点与被分裂节点在同一层,因此leaf属性应该和被分裂节点一样right.leaf = split.leaf;right.keyNumber = t - 1;//如果被分裂节点不是叶子节点,也需要将孩子节点一并拷贝到right节点中if (!split.leaf) {System.arraycopy(split.children, t, right.children, 0, t);}split.keyNumber = t - 1;//将t-1节点放入父结点中int mid = split.keys[t - 1];parent.insertKey(mid, index);parent.insertChild(right, index + 1);
}实现新增
- 首先查找本节点中的插入位置 i,如果没有空位(key 被找到),应该走更新的逻辑。
- 接下来分两种情况
- 如果节点是叶子节点,可以直接插入了
- 如果节点是非叶子节点,需要继续在 children[i] 处继续递归插入
- 无论哪种情况,插入完成后都可能超过节点 keys 数目限制,此时应当执行节点分裂
- 参数中的 parent 和 index 都是给分裂方法用的,代表当前节点父节点,和分裂节点是第几个孩子
具体实现代码如下
public void put(int key) {doPut(null, 0, root, key);
}private void doPut(Node parent, int index, Node node, int key) {int i = 0;while (i < node.keyNumber && node.keys[i] < key) {i++;}// TODO i<node.keyNumber是否多余?if (i < node.keyNumber && node.keys[i] == key) {return;}if (node.leaf) {node.insertKey(key, i);} else {doPut(node, i, node.children[i], key);}if (isFull(node)) {split(parent, index, node);}
}private boolean isFull(Node node) {return node.keyNumber == MAX_KEY_NUMBER;
}实现删除
删除节点会存在下面几种情况
case 1:当前节点是叶子节点,没找到。直接返回null
case 2:当前节点是叶子节点,找到了。直接移除节点即可
case 3:当前节点是非叶子节点,没找到。递归寻找孩子节点是否存在该key
case 4:当前节点是非叶子节点,找到了。找到后驱节点交换key,并将交换后的key删除
case 5:删除后 key 数目 < 下限(不平衡)。需要进行调整
在兄弟节点中keyNumber数量充足的情况下可以通过旋转调整平衡。图示如下
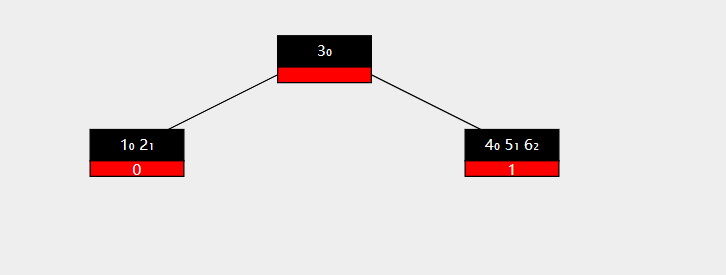
现在要删除节点 2
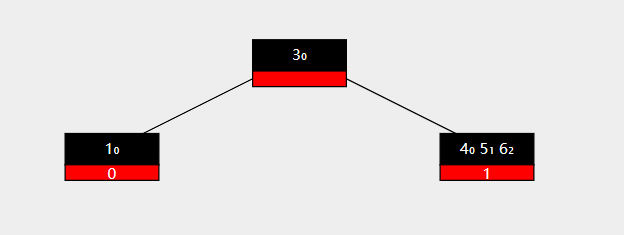
删除之后,左侧孩子的key数量少于最小限度,因此需要进行一次左旋。

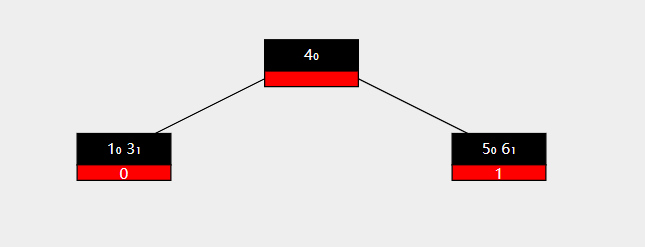
父结点 3 移动到左侧孩子节点中,右侧孩子节点中的第一个key 5 移动到父结点中,左旋结束。
但如果兄弟节点的key数量是最小限度,那么此时应该进行合并,而不是旋转。
合并时,我们通常选择将右侧的节点合并到左侧节点中去。图示如下
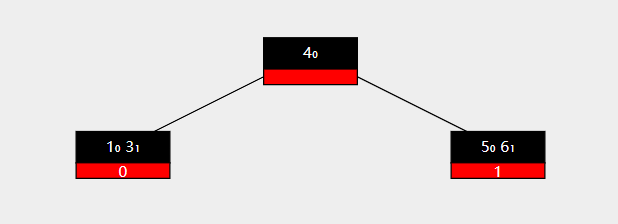
此时要删除key 3 ,右侧兄弟节点无法再向被删除节点提供key。
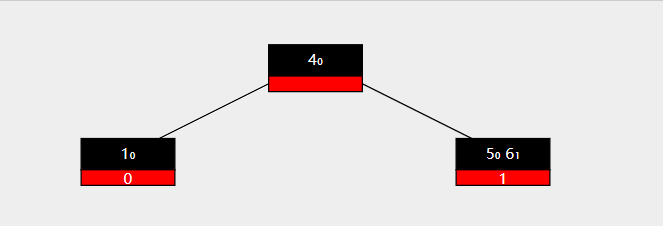


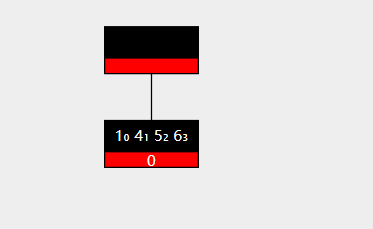
于是将右侧节点移除,同时将父结点的值与被移除节点的值都放在最初的左孩子节点中。
case 6:根节点
当经过合并之后,根结点可能会存在为null的情况,此时让根节点中的 0 号孩子替代掉根节点就好。
具体实现代码如下
/*** 移除指定元素** @param key*/
public void remove(int key) {doRemove(null,root,0, key);
}private void doRemove(Node parent,Node node,int index, int key) {//首先要获取指定元素int i = 0;while (i < node.keyNumber && node.keys[i] < key) {i++;}if (node.leaf) {if (node.keys[i] == key) {//case 2:如果找到了并且是叶子节点node.removeKey(i);} else {//case 1:如果没找到并且是叶子节点return;}} else {if (node.keys[i] == key) {//case 4:如果找到了但不是叶子节点//找到后驱节点并交换位置Node child = node.children[i + 1];while (!child.leaf) {child = child.children[0];}int nextKey = child.keys[0];node.keys[i] = nextKey;//之所以不直接调用孩子节点的removeKey方法是为了避免删除后发生不平衡//child.removeKey(0);doRemove(node,child,i+1, nextKey);} else {//case 3:如果没找到但不是叶子节点doRemove(node,node.children[i],i, key);}}//如果删除后,节点中的key少于下限,那么需要进行调整if (node.keyNumber < MIN_KEY_NUMBER) {//平衡调整balance(parent,node,index);}
}/*** 调整B树** @param parent 父结点* @param node 被调整节点* @param index 被调整节点在父结点中的孩子数组下标*/
private void balance(Node parent, Node node, int index) {//case 6 根节点if (node == root) {if (node.keyNumber==0 && node.children[0]!=null){root = node.children[0];}return;}Node leftChild = parent.leftSibling(index);Node rightChild = parent.rightSibling(index);//如果左边孩子节点中的key值充足if (leftChild != null && leftChild.keyNumber > MIN_KEY_NUMBER) {//将父结点中的key赋值给nodenode.insertKey(parent.keys[index - 1], 0);if (!leftChild.leaf) {//如果左侧孩子不是一个叶子节点,在旋转过后,会导致keysNumber+1!=children。//因此将多出来的孩子赋值更多出来一个key的被调整节点node.insertChild(leftChild.removeRightmostChild(), 0);}//将左孩子中最右侧元素赋值给父结点parent.keys[index - 1] = leftChild.removeRightmostKey();return;}//如果右边充足if (rightChild != null && rightChild.keyNumber > MIN_KEY_NUMBER) {node.insertKey(parent.keys[index], node.keyNumber);if (!rightChild.leaf) {node.insertChild(rightChild.removeLeftmostChild(), node.keyNumber);}parent.keys[index] = rightChild.removeLeftmostKey();return;}//合并//如果删除节点存在左兄弟,向左合并if (leftChild != null) {//将被删除节点从父结点上移除parent.removeChild(index);//将父结点的被移除节点的前驱节点移动到左兄弟上leftChild.insertKey(parent.removeKey(index - 1), leftChild.keyNumber);node.moveToTarget(leftChild);} else {//如果没有左兄弟,那么移除右兄弟节点,并将右兄弟移动到被删除节点上。parent.removeChild(index+1);node.insertKey(parent.removeKey(index),node.keyNumber);rightChild.moveToTarget(node);}
}完整代码
public class BTree {private Node root;private int t;//最小度数private final int MAX_KEY_NUMBER;private final int MIN_KEY_NUMBER;public BTree(int t) {this.t = t;root = new Node(t);MAX_KEY_NUMBER = 2 * t - 1;MIN_KEY_NUMBER = t-1;}static class Node {boolean leaf = true; //是否是叶子节点int keyNumber; //有效keyint t; //最小度int[] keys; // keys数组Node[] children; //孩子节点数组public Node(int t) {this.t = t;this.keys = new int[2 * t - 1];this.children = new Node[2 * t];//最大孩子节点个数为为2*t}@Overridepublic String toString() {return Arrays.toString(Arrays.copyOfRange(keys, 0, keyNumber));}/*** 根据key获取对应节点** @param key* @return*/Node get(int key) {int i = 0;while (i < keyNumber) {//如果在该节点找到,那么直接返回即可if (keys[i] == key) {return this;}//说明要找的元素可能在children[i]中if (keys[i] > key) {break;}i++;}//如果是叶子节点,直接返回nullif (leaf) {return null;}return children[i].get(key);}/*** 指定位置插入元素** @param key* @param index*/void insertKey(int key, int index) {System.arraycopy(keys, index, keys, index + 1, keyNumber - index);keys[index] = key;keyNumber++;}/*** 向节点中插入孩子节点** @param child* @param index*/void insertChild(Node child, int index) {System.arraycopy(children, index, children, index + 1, keyNumber - index);children[index] = child;}//移除指定元素int removeKey(int index) {int t = keys[index];System.arraycopy(keys, index + 1, keys, index, --keyNumber - index);return t;}//移除最左边的元素int removeLeftmostKey() {return removeKey(0);}//移除最右边的元素int removeRightmostKey() {return removeKey(keyNumber - 1);}//移除指定位置的孩子节点Node removeChild(int index) {//获取被移除的节点Node t = children[index];//将被移除节点的后面元素向前移动一位System.arraycopy(children, index + 1, children, index, keyNumber - index);//将之前最后一位的引用释放children[keyNumber] = null;//返回被引用元素return t;}//移除最左边的孩子节点Node removeLeftmostChild() {return removeChild(0);}//移除最右边的孩子节点Node removeRightmostChild() {return removeChild(keyNumber);}//移动指定节点到目标节点void moveToTarget(Node target) {int start = target.keyNumber;if (!leaf) {for (int i = 0; i <= keyNumber; i++) {target.children[start + i] = children[i];}}for (int i = 0; i < keyNumber; i++) {target.keys[target.keyNumber++] = keys[i];}}//获取指定孩子节点的左边节点Node leftSibling(int index) {return index > 0 ? children[index - 1] : null;}//获取指定孩子节点的右边节点Node rightSibling(int index) {return index == keyNumber ? null : children[index + 1];}}/*** 查询key值是否在树中** @param key* @return*/public boolean contains(int key) {return root.get(key) != null;}/*** 新增节点** @param key*/public void put(int key) {doPut(null, 0, root, key);}//index的作用是,给分割方法提供参数private void doPut(Node parent, int index, Node node, int key) {//寻找插入位置int i = 0;while (i < node.keyNumber && node.keys[i] < key) {i++;}//如果找到了,直接更新if (node.keys[i] == key) {return;}//如果没找到,查看是否是叶子节点,如果不是,向下寻找if (node.leaf) {node.insertKey(key, i);} else {doPut(node, i, node.children[i], key);}if (isFull(node)) {split(parent, index, node);}}private boolean isFull(Node node) {return node.keyNumber == MAX_KEY_NUMBER;}/*** 分裂节点** @param parent* @param index 分割节点在父结点的孩子下标* @param split*/private void split(Node parent, int index, Node split) {if (parent == null) {//说明分割根节点,除了需要创建right节点之外,还需要创建parent节点parent = new Node(t);parent.leaf = false;parent.insertChild(split, 0);root = parent;}Node right = new Node(t);//将被分裂节点的一部分key放入right节点中。System.arraycopy(split.keys, t, right.keys, 0, t - 1);//新建的节点与被分裂节点在同一层,因此leaf属性应该和被分裂节点一样right.leaf = split.leaf;right.keyNumber = t - 1;//如果被分裂节点不是叶子节点,也需要将孩子节点一并拷贝到right节点中if (!split.leaf) {System.arraycopy(split.children, t, right.children, 0, t);for (int i =t;i<=split.keyNumber;i++){split.children[i]=null;}}split.keyNumber = t - 1;//将t-1节点放入父结点中int mid = split.keys[t - 1];parent.insertKey(mid, index);parent.insertChild(right, index + 1);}/*** 移除指定元素** @param key*/public void remove(int key) {doRemove(null,root,0, key);}private void doRemove(Node parent,Node node,int index, int key) {//首先要获取指定元素int i = 0;while (i < node.keyNumber && node.keys[i] < key) {i++;}if (node.leaf) {if (node.keys[i] == key) {//case 2:如果找到了并且是叶子节点node.removeKey(i);} else {//case 1:如果没找到并且是叶子节点return;}} else {if (node.keys[i] == key) {//case 4:如果找到了但不是叶子节点//找到后驱节点并交换位置Node child = node.children[i + 1];while (!child.leaf) {child = child.children[0];}int nextKey = child.keys[0];node.keys[i] = nextKey;//之所以不直接调用孩子节点的removeKey方法是为了避免删除后发生不平衡//child.removeKey(0);doRemove(node,child,i+1, nextKey);} else {//case 3:如果没找到但不是叶子节点doRemove(node,node.children[i],i, key);}}//如果删除后,节点中的key少于下限,那么需要进行调整if (node.keyNumber < MIN_KEY_NUMBER) {//平衡调整balance(parent,node,index);}}/*** 调整B树** @param parent 父结点* @param node 被调整节点* @param index 被调整节点在父结点中的孩子数组下标*/private void balance(Node parent, Node node, int index) {//case 6 根节点if (node == root) {if (node.keyNumber==0 && node.children[0]!=null){root = node.children[0];}return;}Node leftChild = parent.leftSibling(index);Node rightChild = parent.rightSibling(index);//如果左边孩子节点中的key值充足if (leftChild != null && leftChild.keyNumber > MIN_KEY_NUMBER) {//将父结点中的key赋值给nodenode.insertKey(parent.keys[index - 1], 0);if (!leftChild.leaf) {//如果左侧孩子不是一个叶子节点,在旋转过后,会导致keysNumber+1!=children。//因此将多出来的孩子赋值更多出来一个key的被调整节点node.insertChild(leftChild.removeRightmostChild(), 0);}//将左孩子中最右侧元素赋值给父结点parent.keys[index - 1] = leftChild.removeRightmostKey();return;}//如果右边充足if (rightChild != null && rightChild.keyNumber > MIN_KEY_NUMBER) {node.insertKey(parent.keys[index], node.keyNumber);if (!rightChild.leaf) {node.insertChild(rightChild.removeLeftmostChild(), node.keyNumber);}parent.keys[index] = rightChild.removeLeftmostKey();return;}//合并//如果删除节点存在左兄弟,向左合并if (leftChild != null) {//将被删除节点从父结点上移除parent.removeChild(index);//将父结点的被移除节点的前驱节点移动到左兄弟上leftChild.insertKey(parent.removeKey(index - 1), leftChild.keyNumber);node.moveToTarget(leftChild);} else {//如果没有左兄弟,那么移除右兄弟节点,并将右兄弟移动到被删除节点上。parent.removeChild(index+1);node.insertKey(parent.removeKey(index),node.keyNumber);rightChild.moveToTarget(node);}}}
相关文章:

数据结构与算法【B树】的Java实现+图解
目录 B树 特性 实现 节点准备 大体框架 实现分裂 实现新增 实现删除 完整代码 B树 也是一种自平衡的树形数据结构,主要用于管理磁盘上的数据管理(减少磁盘IO次数)。而之前说的AVL树与红黑树适合用于内存数据管理。存储一个100w的数…...
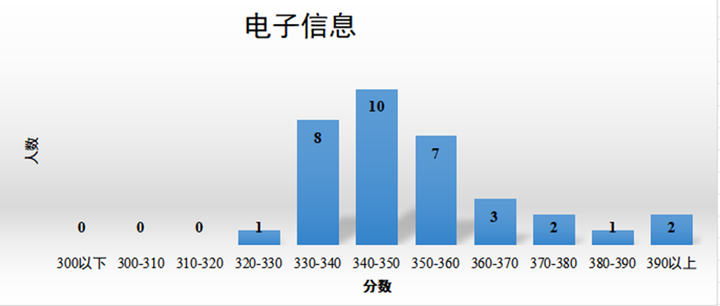
2024中国人民大学计算机考研分析
24计算机考研|上岸指南 中国人民大学 中国人民大学计算机考研招生学院是信息学院。目前均已出拟录取名单。 中国人民大学在1978年创立了经济信息管理系,它是国内最早建立的将数学与信息技术在经济管理领域应用为特色的系科。1986年,在原系计算站的基础…...

无人智能货柜:提升购物体验
无人智能货柜:提升购物体验 随着移动支付的普及,人们日常生活中的主要场景已经渗透了这一支付方式。同时,无人智能货柜作为购物的重要渠道,正在崭露头角。通过人工智能、图像识别和物联网技术的应用,无人智能货柜将使购…...
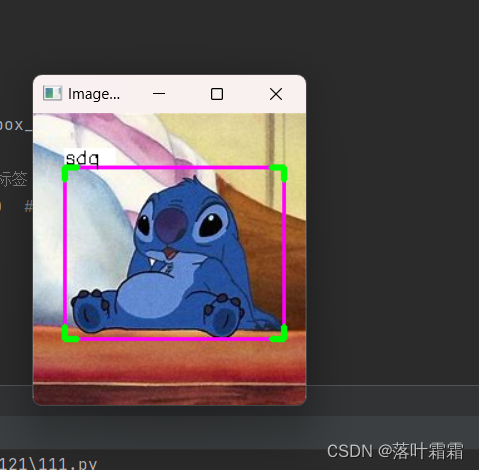
【OpenCV实现图像:可视化目标检测框】
文章目录 概要画框函数代码实现标签美化角点美化透明效果小结 概要 目标检测框的可视化在计算机视觉和机器学习领域中是一项重要的任务,有助于直观地理解和评估目标检测算法的性能。通过使用Python和相关的图像处理库,可以轻松实现目标检测框的可视化。…...

C/C++---------------LeetCode第1436. 旅行终点站
旅行的终点站 题目及要求哈希算法在main内使用 题目及要求 给你一份旅游线路图,该线路图中的旅行线路用数组 paths 表示,其中 paths[i] [cityAi, cityBi] 表示该线路将会从 cityAi 直接前往 cityBi 。请你找出这次旅行的终点站,即没有任何可…...

如何在AD上创建完整的项目
首先,我们先安装好AD,这里我使用的是AD22,安装过程如下: Altium Designer 22下载安装教程-CSDN博客 Altium Designer 22是全球领先的PCB设计软件之一,为电路板设计师提供了一种集成的解决方案,旨在简化和加…...
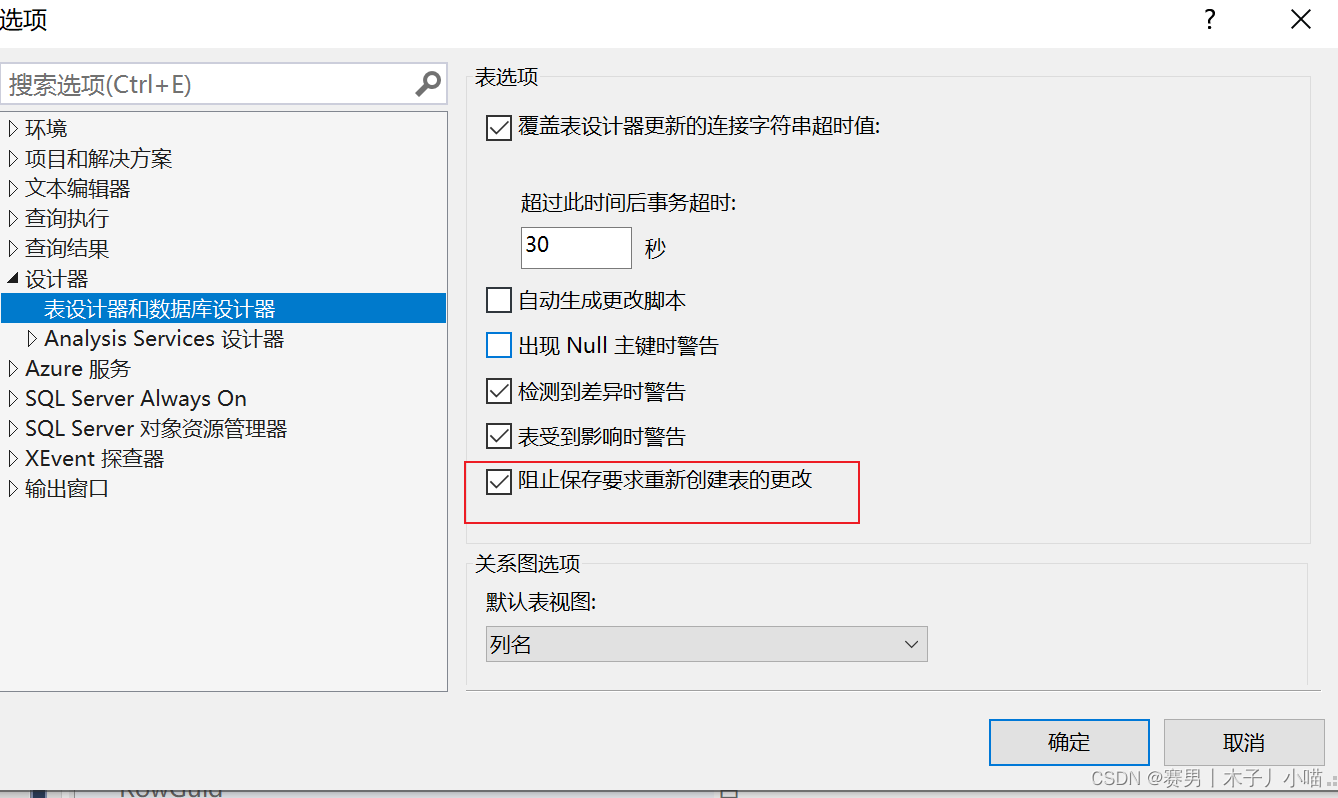
实时错误’-2147217887‘多步OLB DB 操作产生错误。如果可能,请检查OLE DB状态值
目录 背景问题问题分析问题解决 错误解决与定位技巧总结 背景 仍旧是学生信息管理系统的问题,当时做的时候没发现这么多问题呢,只能说明一件事,做的时候没有站在用户的角度考虑需求,设置了什么内容,就按照设置好的去测…...
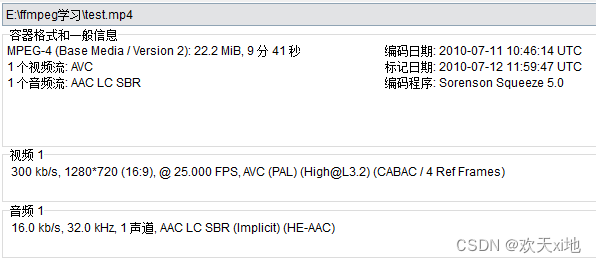
九、ffmpeg命令转封装
开了几天小差,今天继续学习ffmpeg。 准备测试使用的视频,并查看其信息 # 查看视频信息。使用Mediainfo也可以 ffprobe test.mp4 视频格式的信息如下。 保持编码格式:ffmpeg -i test.mp4 -vcodec copy -acodec copy test_copy.tsffmpeg -i…...
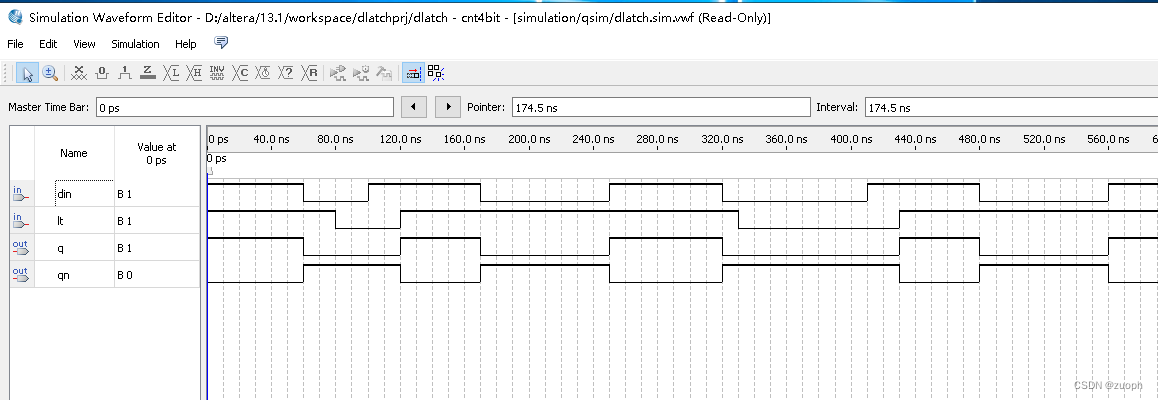
数字逻辑电路基础-时序逻辑电路之锁存器
文章目录 一、锁存器简介二、verilog源码三、综合及仿真结果 一、锁存器简介 本文介绍数字逻辑电路中一种常用的基础时序逻辑电路-锁存,顾名思义,它的功能就是将输入在控制信号有效时透明传输到输出端,当控制信号无效时,输出值保…...
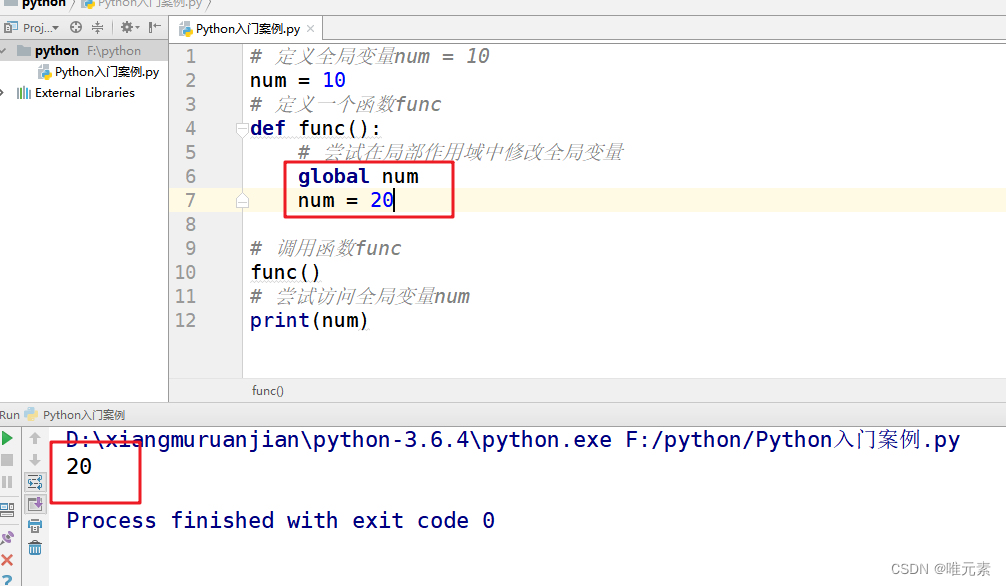
Python---global关键字---设置全局变量
global 英 /ˈɡləʊb(ə)l/ adj. 全球的,全世界的;全面的,整体的;(计算机)全局的;球形的 需求:如果有一个数据,在函数A和函数B中都要使用,该怎么办&…...

bug场景记录
项目场景: mapper.xml文件中sql语句执行失败,显示输入的参数数量不对 问题描述 <select id"page" resultType"com.sky.entity.Employee">select * from employee<where><if test"name ! null and name !"…...

【云备份】第三方库的认识与使用
文章目录 json库粗略认识详细认识writer 类reader类jsoncpp序列化实现jsoncpp反序列化实现 bundle文件压缩库简单认识bundle库实现文件压缩bundle库实现文件解压缩 httplib库Request类Response类Server类Client类 json库 粗略认识 json是一种数据交换格式,采用完全…...

6.2.SDP协议
那今天呢?我们来介绍一下sdp协议,那实际上呢?sdp协议非常的简单。我们如果拿到一个stp的文档去看的话,那你要分阅里边的所有的内容会觉得很枯燥,但实际上呢,如果我们按照这张图所展示的结构去看stp的话。你…...

[汇编实操]DOSBox工具安装——Ubuntu18.04系统
一、下载&安装 sudo apt install -y dosbox 二、启动 dosbox 三、C盘挂载 将上述文件下载放在任意路径,将DEBUG目录映射为虚拟C盘 MASM.EXE 是用来编译的,LINK.EXE 用来链接,这俩是必须的。 执行如下命令: mount c /m…...

前端 HTML 的 DOM 事件相关知识有哪些?
HTML 的 DOM 事件是指在网页上发生的各种事件,如点击、鼠标移动、键盘输入等。 通过 JavaScript 脚本可以对这些事件进行监听和处理,以实现交互效果。以下是一些常见的 DOM 事件及其相关知识点: 1、click:点击事件,在…...
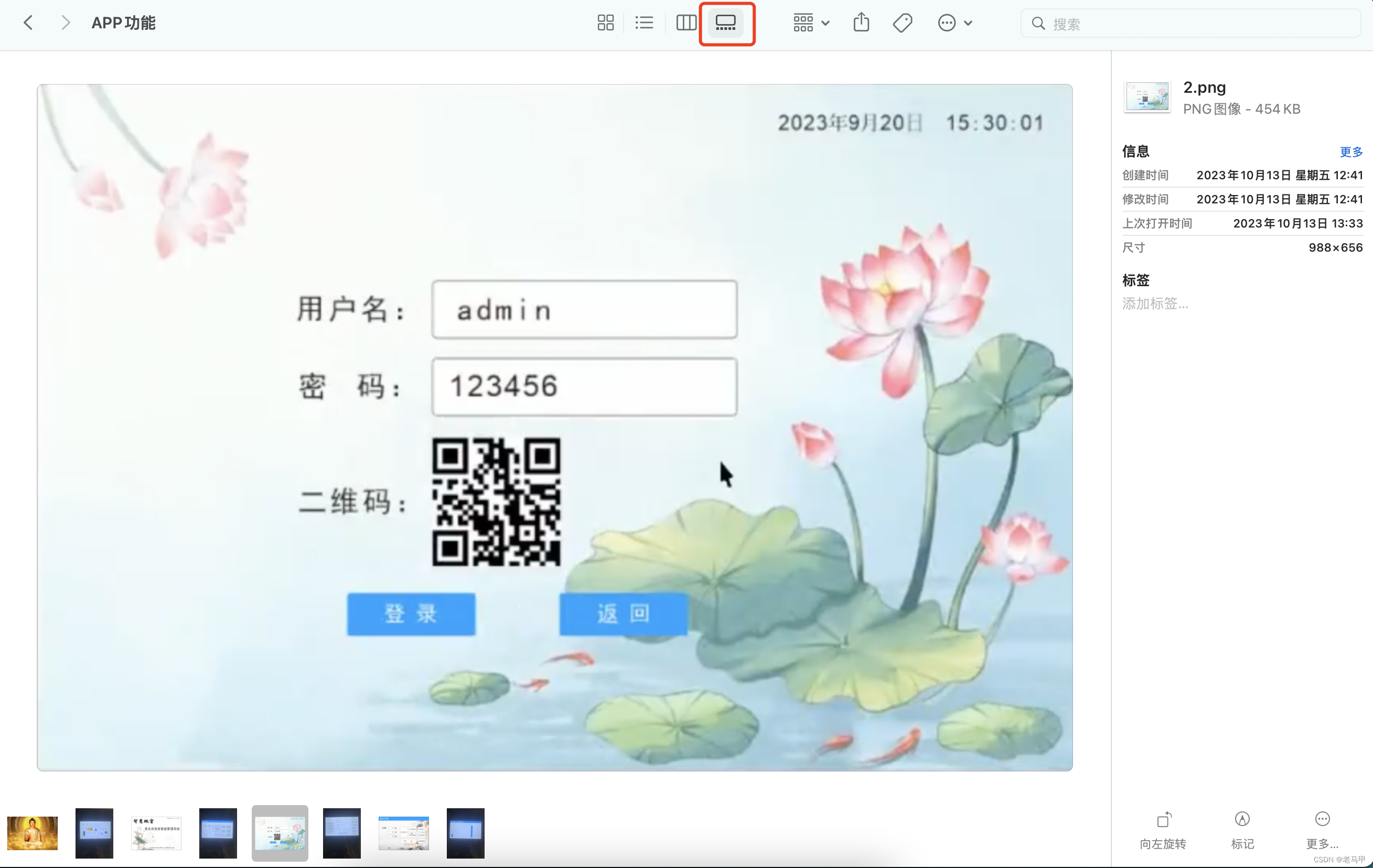
Mac自带的看图如何连续查看多张图片
一、问题 mac看访达里的图片时,双击打开一张图片,然后按上下左右键都没法切换到另外的图片。而且也没找到像window一样单击缩略图可以看到预览图。其实是自己不懂得怎么使用,哈哈哈😂 二、方法 2.1、图标方式 可以看到缩略图&a…...
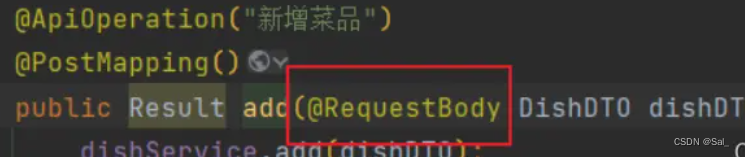
HTTP四大参数类型及请求参数的方式和如何接收
HTTP 请求中4大参数类型和接收方法。 1、请求头参数head 请求头参数顾名思义,是存放在请求头中发送给服务器的参数,服务器通过解析请求头获取参数内容。通常会存放本次请求的基本设置,以帮助服务器理解并解析本次请求的body体。 参数形式如…...

【C++11】default、delete与Noncopyable
C11 oop中的default、delete与Noncopyable default 在C11标准中,可以使用default关键字来显式地声明默认的构造函数和析构函数。 使用default关键字可以用来显式声明默认的构造函数和析构函数。这样做可以让编译器自动生成默认实现 –>->->关于构造函数…...
【心得】基于flask的SSTI个人笔记
目录 计算PIN码 例题1 SSTI的引用链 例题2 SSTI利用条件: 渲染字符串可控,也就说模板的内容可控 我们通过模板 语法 {{ xxx }}相当于变相的执行了服务器上的python代码 利用render_template_string函数参数可控,或者部分可控 render_…...

ubuntu20.04 nginx 部署静态网页
1、安装nginx Ubuntu环境下安装部署Nginx(有网)_ubuntu 安装nginx_荒Huang的博客-CSDN博客 2、压缩并上传文件到服务器指定位置(unzip命令),修改nginx配置文件,指定root目录为文件的目录,index 值为指定的html文件 …...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
