leedcode 刷题 - 除自身以外数组的乘积 - 和为 K 的子数组
I238. 除自身以外数组的乘积 - 力扣(LeetCode)
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]提示:2 <= nums.length <= 105
-30 <= nums[i] <= 30
保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内进阶:你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)题目已经给的很明显了,就是使用前缀积 和 后缀积 的方式来求解,这种方式其实 是一个简化的 动态规划。
用两个数组,分别存储 从起始位置到 i 位置的乘积 和 从 末尾位置 到 i 位置的乘积;
上述两个结果对应的就是 f[i] 和 g[i] 。
递推公式:
f[i] = f[i - 1] * nums[i - 1];g[i] = g[i + 1] * nums[i + 1];f[0] 和 g[nums.size()] 都是需要自己手动算的,上述递推公式是算不出来的。
如果我们像计算题目描述的某个位置(比如是 i 位置)的 前缀积 和 后缀积的话,只需要计算 f[i] * g[i] 既可,因为 f[i] 表示的就是 i 之前的 所有积,g[i] 表示的就是 i 之后的所有的积。
完整代码:
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {vector<int> f(nums.size(), 1);vector<int> g(nums.size(), 1);vector<int> ret(nums.size());for(int i = 1;i < nums.size(); i++) f[i] = f[i - 1] * nums[i - 1];for(int i = nums.size() - 2; i >= 0; i--) g[i] = g[i + 1] * nums[i + 1];for(int i = 0;i < nums.size();i++) ret[i] = g[i] * f[i];return ret;
}
};I560. 和为 K 的子数组 - 力扣(LeetCode)
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1:输入:nums = [1,1,1], k = 2
输出:2
示例 2:输入:nums = [1,2,3], k = 3
输出:2还是使用前缀和,我们可以使用 找到一个前缀和 sum[i] 就表示,从数组 0 号位置开始,到 i 位置的所有元素之和。
那么,我们只需要在这个区间当中找到 在 [0,i] 这个区间当中,某一个位置作为起始位置(假设为 j ),到 i 位置,这个子数组的 元素之和等于k,那么 ,[0,j] 这个区间当中各个 元素之和就是 sum[i] - k;
往后,只需要 i 往后寻找,就不会找漏。
但是,上述还是有一个问题,如果我们直接遍历 sum 数组的,来找到 j 这个位置的话,在加上 创建 sum 数组的时间复杂度,实际上,这个算法的整个 时间复杂度其实还不如 暴力解法。
所以,其实我们不用 循环一个一个 去找 j 位置,我们可以利用一个 hash 表来 代替 sum 存储的这些 前缀和的值,也就是代替 sum 存储 其中的每一个元素。
哈希表: hash<前缀和值, 前缀和出现次数>
这样,如果我们 想 在 [0,i] 这个区间当中, 找到 j 这个位置,只需要 利用 hash 表的快速查找来查找 在当前hash 表当中有没有 sum[i] - k 这个前缀和,同时,利用 hash 表当中的 count()函数,可以快速查找,这个 sum[i] - k 出现次数。
关于前缀和加入hash 表的时机:
因为我们的前缀和算法,是要找的是 在 [0,i] 这个区间当中 ,有多少个 前缀和 等于sum[i] - k; 。
如果直接 在一开始就把 sum 计算出来,然后把 区间当中 前缀和 和 前缀和出现的次数加入到 hash 表当中是会计算到 i 后面的值。所以不行。
所以,我们在计算 i 位置之前,哈希表里面值存储 [0, i - 1] 位置的前缀和。
还有一种情况,当 当前的整个的 前缀和 等于 k 的话,那么,在上述的算法当中,其实我们是找不到这个情况的,因为 我们找到的是 等于 k 的子区间,这个子区间的起始位置上述说过了,是 j ,那么 满足 sum[i] - k; 的 区间就是 [0, j - 1], 那么在这个情况当中就是 [0, -1] 这个区间,这个区间是不存在的。
所以,我们开始就要默认 数组当中有一个 和为 0 的前缀和,即: hash[0] = 1;
完整代码:
class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> hash(nums.size());hash[0] = 1;int sum = 0, ret = 0; // sum 代替sum数组,利用变量给 hash 当中赋值;ret 返回个数for(auto& e : nums){sum += e; // 计算当前的前缀和// 计算满足 条件的区间,是否在 hash 当中出现。count()函数判断是否出现// 出现计数器 加上 这个前缀和 在 hash 当中出现的次数if(hash.count(sum - k)) ret += hash[sum - k]; hash[sum]++; }return ret;}
};I974. 和可被 K 整除的子数组 - 力扣(LeetCode)
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的(连续、非空) 子数组 的数目。
子数组 是数组的 连续 部分。
示例 1:输入:nums = [4,5,0,-2,-3,1], k = 5
输出:7
解释:
有 7 个子数组满足其元素之和可被 k = 5 整除:
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例 2:输入: nums = [5], k = 9
输出: 0要解决这道题目,首先要知道 同于定理

也就是 如果 a 和 b 的差值,除上 p ,如果是整除的话,也就是余数是零的话,a 除上 p 的余数 = b 除上 p 的余数。
而且,还需要清楚,在C++ 当中, [负数 % 正数] 的结果是 一个负数。
也就是说,其实[负数 % 正数] 其实结果也是一个 余数,但是这个余数是负数。
所以,针对这种情况,我们要对这个负数进行修正,把他修正为 正数。
所以,当我们在计算 [负数 % 正数] 的 结果之时,其实,计算出的负数的结果在加上 模数(也就是其中的正数),其实就是对应的正数的结果。如下图所示:

上述的计算方式对于 a 是负数的情况来说,计算出的结果就是修正之后的结果,也就是修正为 正数之后的结果。
但是上述的 修正方式对于 a 是正数的情况是 计算错误的,因为 对于 a 是正数的情况来说, a % b 本来就是 正确的结果,但是后面又加上了 一个 b,所以是不正确的。
所以,为了 正数和负数统一,我们共用的方式就是 在上述计算式子当中,再 % b 即可。

上述式子就是我们想要的i修正公式了。
所以,按照和这个问题其实就和上述 和为K的子数组求解方式一样了。
先求出所有的 从 0 号数组位置开始的 所以前缀模,保存到一个数组当中,然后 求出 与 K 模的余数即可。
同样优化方式和上述一样,不需要多定义一个 数组来保存 前缀模,这样也不好 查找对应的前缀模,只需要 用一个 hash表来存储即可。
上述问题就被简化为了 在 [0, i - 1] 这个区间当中,找到有多少个前缀和 的 余数等于 (sum % k + k ) % k。
完整代码:
class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int, int> hash;hash[0 % k] = 1; // 0 这数的余数int sum = 0, ret = 0;for(auto& e : nums){sum += e;int r = (sum%k + k) % k;if(hash.count(r)) ret += hash[r];hash[r]++;}return ret;}
};I525. 连续数组 - 力扣(LeetCode)
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
示例 1:输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。
示例 2:输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。在数组当中,所有的 元素的值要么是 0 ,要么是1。我们需要找到一个 符合要求的最长的连续的子数组,返回这个子数组的长度。
我们在统计个数的时候,其实是可以做到转化的,如果把 0 全部替换为-1,那么我们统计个数的问题,其实就 转化成了 找到一个 元素之和等于 0 的子数组。
所以,这道题目就可以使用前缀和的方法来解决。
使用hash 表来存储 前缀和为 sum 的区间,所以吗,应该是 unordered_map<sum, i > (其中 sum 是前缀和,i 是这个前缀和区间的下标)。
当找到某一个下标,和为 sum,计算出 这个区间的长度,就把这个 对应的 绑定的值存入到哈希表当中。
如果有重复的 sum,但是区间不一样,不需要重新更新原本在 hash 表当中的 <sum , i>, 只需要保留之前存入的 <sum, i> 即可。因为 ,我们需要找到 子区间最长的子数组,那么 下标应该是越考左 ,那么 计算出的 子区间 长度才是最大的。
同样,为了处理特殊情况:当 [0 , i] 这个子区间计算出的前缀和就是0了,那么按照上述 和为K的子数组 这个题目当中逻辑去 找到子区间的话,就会在 -1 为开始的区间去找。
所以,我们需要 在开始 默认 一个子区间的前缀和是0,即 hash[0] = -1;
上述的过程就可以找出所有的 合法的子数组了,现在就是如何计算这个子数组的区间大小?
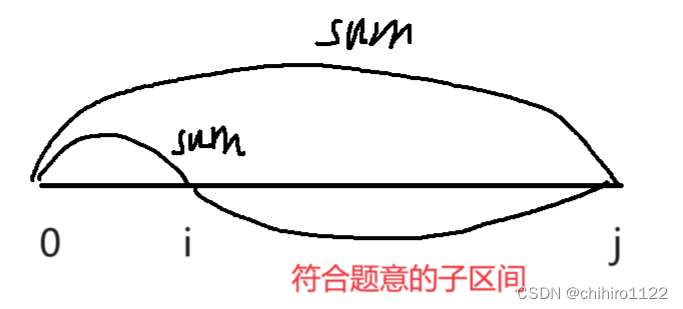
如上,我们只需要找出 i 和 j 两个下标,使得 [0, i] 的 前缀和 和 [0, j] 的前缀和 相等即可。
所以我们计算出的 区间的 长度就是 i - j 。
完整代码:
class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int ,int> hash;hash[0] = -1; // 默认 刚开始 哈希表当中有一个 前缀和为0 的区间int sum = 0, ret = 0;for(int i = 0 ;i < nums.size(); i++){sum += nums[i] == 0 ? -1 : 1; // 如果是 0 就加-1,如是1 就加 1// 如果 sum 在hash 当中存在,说明此时就已经找到了 符合条件的子区间// 那么就更新的 ret 返回值。if(hash.count(sum)) ret = max(ret, i - hash[sum] + 1 - 1);else hash[sum] = i; // sum 在 hash 当中不存在,那么 就添加一个 hash 元素}return ret;}
};相关文章:

leedcode 刷题 - 除自身以外数组的乘积 - 和为 K 的子数组
I238. 除自身以外数组的乘积 - 力扣(LeetCode) 给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在…...
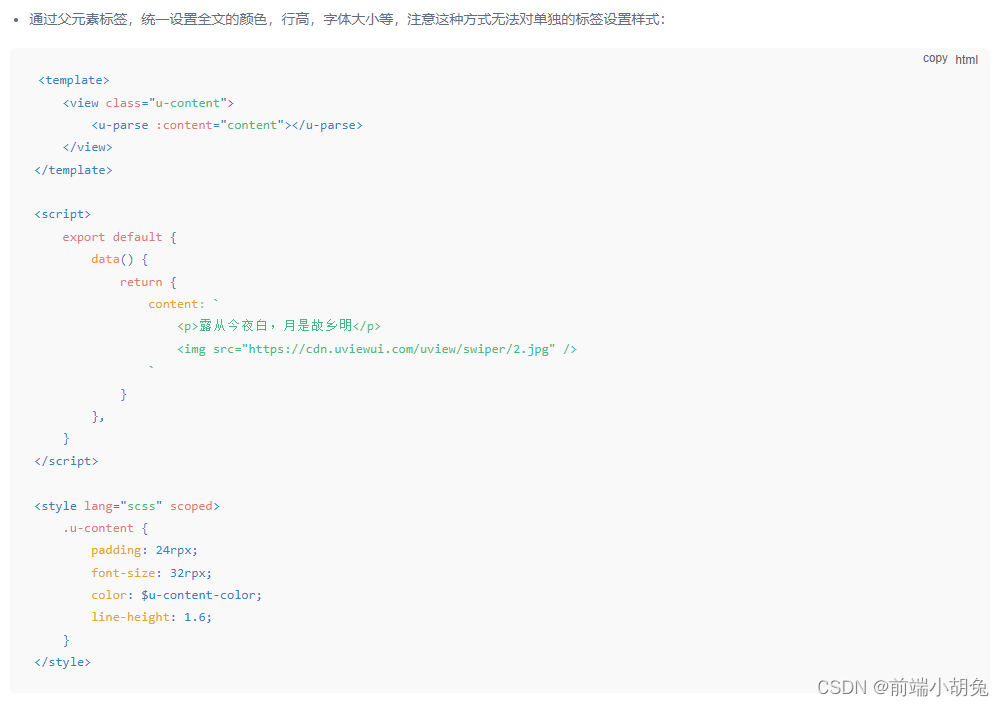
uniapp 富文本以及移动端富文本的展示问题
富文本展示有几种方式: 1.<view v-html"content"></view> 2. uniapp自带组件 rich-text rich-text | uni-app官网 <rich-text :nodes"content"></rich-text> 3.uView组件 u-parse Parse 富文本解析器 | uView 2.0 - 全面兼…...

JAVA sql 查询
-- 1. 查询员工表所有数据,并说明使用*的缺点 SELECT * from employees -- *号查询效率低 -- 2. 查询所员工的 email 全名,公司 email 统一以 "qq.com " 结尾. SELECT email from employees WHERE email like "%qq.com" -- 3. 打印公司里…...

掌握Katalon Studio 导入 swagger 接口文档,接口测试效率提升100%
katalon studio大家都已经不陌生了,是一款现在非常主流的自动化测试工具,包括了web、api、APP,甚至PC应用程序都可以使用它来完成自动化测试。 swagger是一款RESTFUL接口的文档在线自动生成软件,swagger是一个规范和完整的框架&a…...

程序员最奔溃的瞬间
作为一名程序员,我刚刚步入职场不久,经历了许多有趣又令人崩溃的瞬间。这些瞬间让我既感到气馁又好笑,同时也让我更加坚定了对编程的热爱和追求。 首先,我想分享一个令我崩溃的瞬间。有一天,我在调试一个复杂的bug时花…...

java字符串的常见用法
java字符串的常见用法 Java中的字符串是一个非常常用的对象,它属于Java的内置类String类的实例。字符串在Java中是不可变的,即一旦创建了一个字符串对象,就不能修改它的值。 下面是一些关于Java字符串的详细用法: 1)创…...
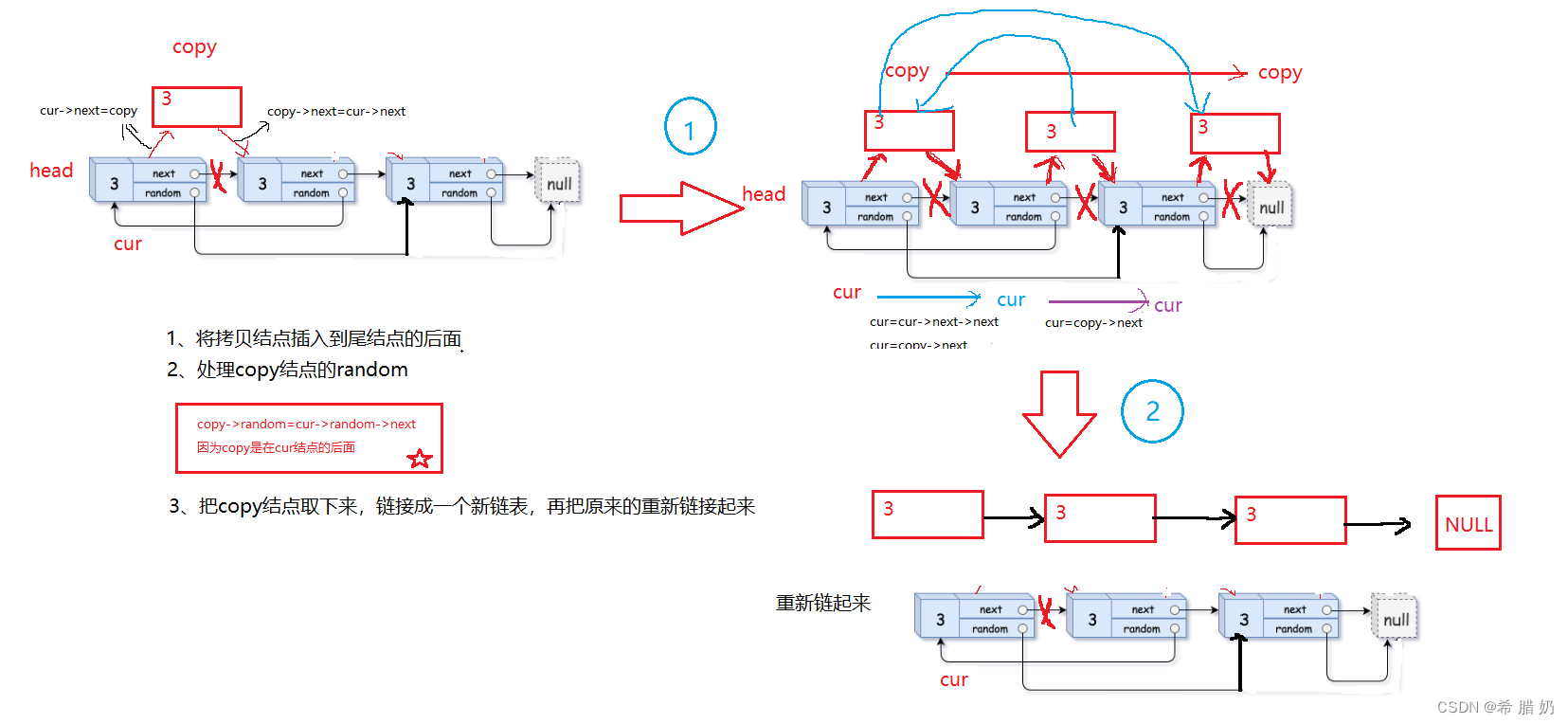
链表OJ--下
文章目录 前言一、链表分割二、环形链表I三、环形链表II四、链表的回文结构五、随机链表的复制 前言 一、链表分割 牛客网CM11:链表分割- - -点击此处传送 题解: 思路图: 代码: 二、环形链表I 力扣141:环形链表…...

FreeRTOS源码阅读笔记4--semphr.h
信号量是特殊的队列--无法存储消息的队列,相关的接口函数声明在semphr.h中,通过宏定义替换队列函数实现。 4.1创建二值信号量xSemaphoreCreateBinary() 4.1.1函数原型 queueQUEUE_TYPE_BINARY_SEMAPHORE:一个宏,表示创建队列的…...

面试:MyBatis问题
文章目录 什么是MyBatis?MyBatis的核心组件有哪些?能说说MyBatis的工作原理吗?MyBatis的工作流程是怎样的?Mybaits 的优点 & 缺点MyBatis 与 JPA 有哪些不同?MyBatis一二级缓存的区别?MyBatis如何处理延迟加载&am…...
跳转及传值的几种方式 router-link + query + params)
vue中页面(路由)跳转及传值的几种方式 router-link + query + params
vue中页面(路由)跳转及传值的几种方式 知道query 和 params 是什么 参考文案:https://www.php.cn/js-tutorial-382859.html 跳转的几种方式与传值 1、router-link 1.1 根据路由路径(无参数与有参数) <router-link to = "/page">跳转到page页面</…...
媒体格式转换软件Permute 3 mac中文版软件特点
Permute mac是一款媒体格式转换软件,可以帮助用户快速地将各种音频、视频和图像文件转换成所需格式,并提供了一些常用工具以便于用户进行编辑和处理。 Permute mac软件特点 - 支持大量格式:支持几乎所有常见的音频、视频和图像格式ÿ…...

Docker实用篇
Docker实用篇 0.学习目标 1.初识Docker 1.1.什么是Docker 微服务虽然具备各种各样的优势,但服务的拆分通用给部署带来了很大的麻烦。 分布式系统中,依赖的组件非常多,不同组件之间部署时往往会产生一些冲突。在数百上千台服务中重复部署…...
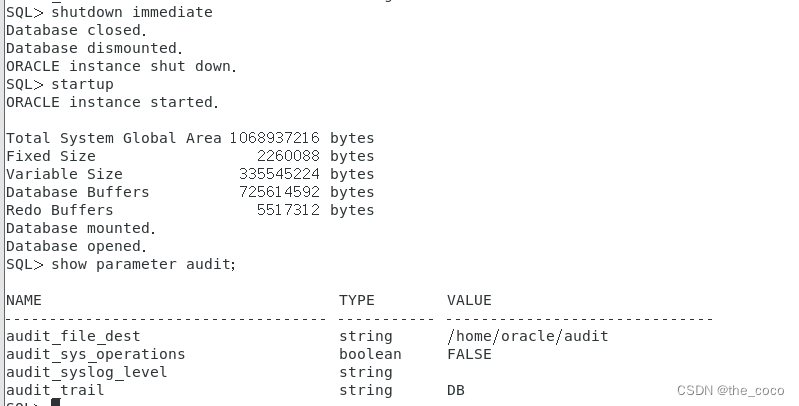
开启数据库审计(db,extended级别或os级别),并将审计文件存放到/home/oracle/audit下
文章目录 开启数据库审计(db,extended级别或os级别),并将审计文件存放到/home/oracle/audit下一. 简介二. 配置2.1. 审计是否安装2.2. 审计表空间迁移2.3. 审计参数2.4. 审计级别2.5. 其他审计选项2.6. 审计相关视图 三. 使用3.1. 开启/关闭审…...

单片机语音芯片开发要解决的问题
在单片机语音芯片开发过程中,可能会遇到多种问题,这些问题可能来自于技术层面,也可能来自于芯片本身的设计和应用层面。下面让我们具体从芯片的功耗、语音识别的准度、芯片的尺寸和芯片的可靠性四个方面开展讨论。 1.芯片的功耗问题 首先&a…...
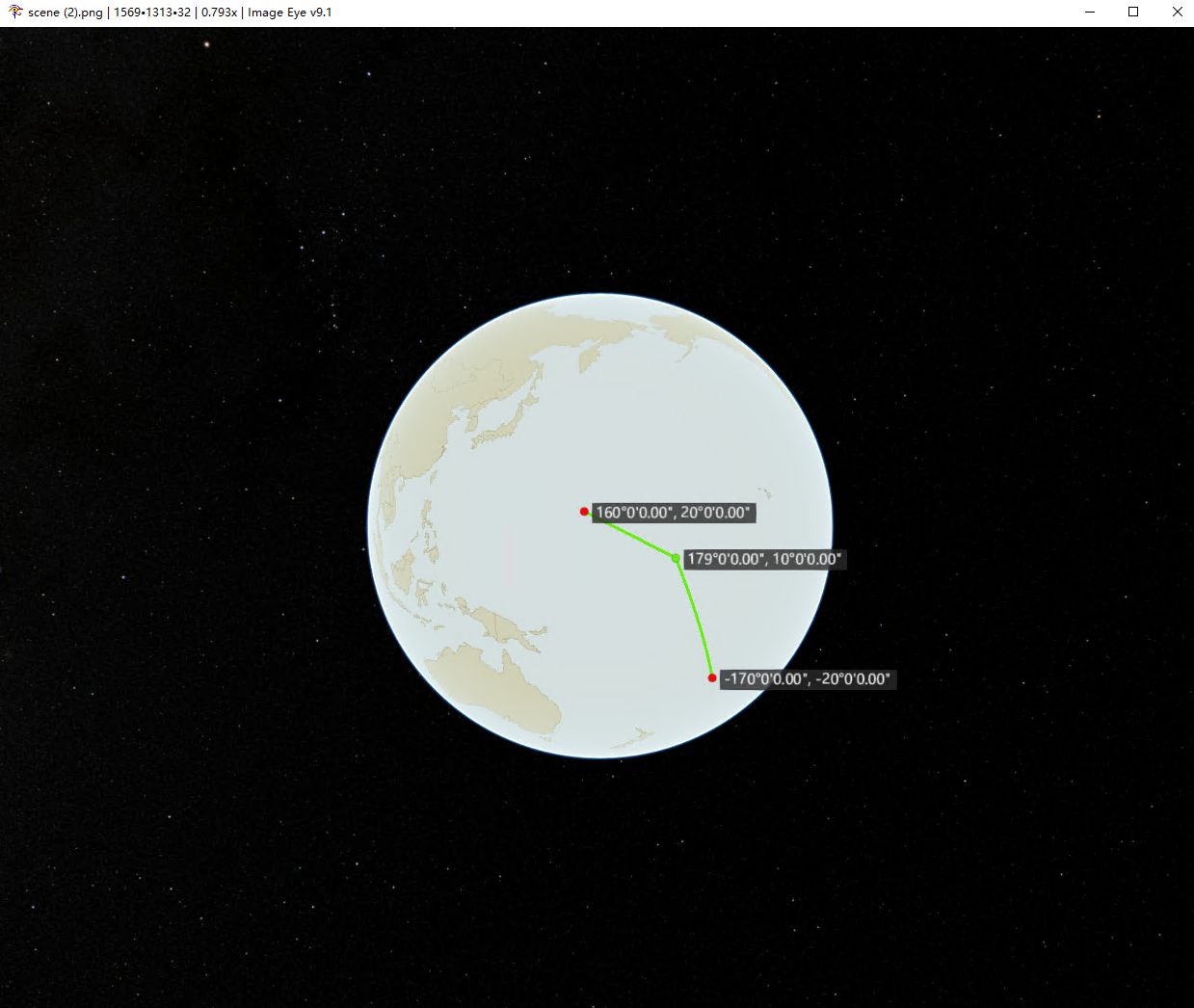
Cesium 展示——地球以及渲染数据导出(下载)为图片或 pdf
文章目录 需求分析新加需求分析第一种方式第二种方式需求 将 Cesium 球体以及渲染数据导出为 jpg/png/pdf 分析 获取场景 scene 信息,转为image 的 octet-stream 流 进行下载为图片 /*** @todo canvas 导出图片* @param {string} dataurl - 地址* @return {Blob}*/ functio…...

大数据平台红蓝对抗 - 磨利刃,淬精兵! | 京东云技术团队
一、背景 目前大促备战常见备战工作:专项压测(全链路压测、内部压测)、灾备演练、降级演练、限流、巡检(监控、应用健康度)、混沌演练(红蓝对抗),如下图所示。随着平台业务越来越复…...
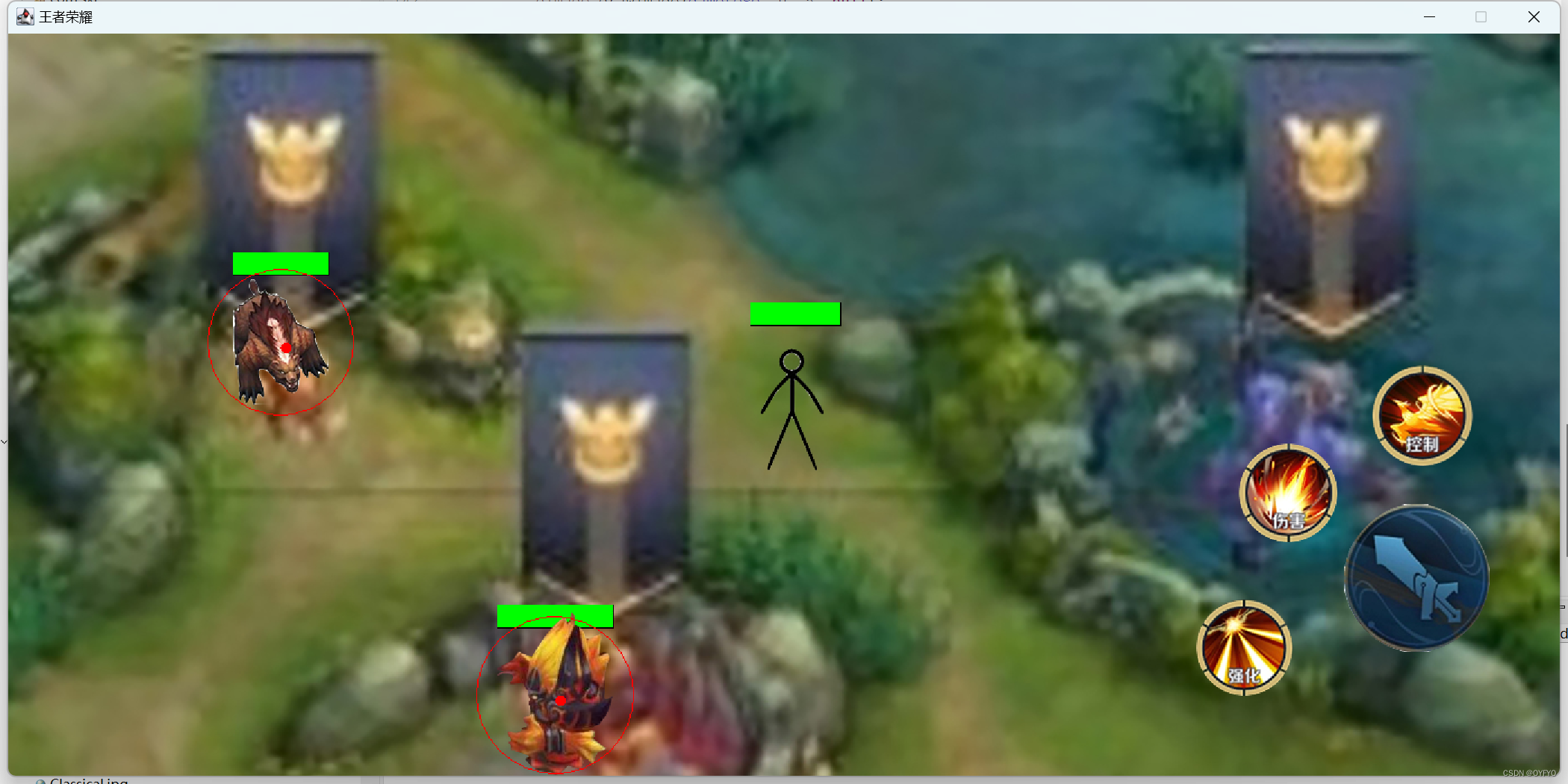
java游戏制作-王者荣耀游戏
一.准备工作 首先创建一个新的Java项目命名为“王者荣耀”,并在src下创建两个包分别命名为“com.sxt"、”com.stx.beast",在相应的包中创建所需的类。 创建一个名为“img”的文件夹来储存所需的图片素材。 二.代码呈现 package com.sxt;import javax.sw…...
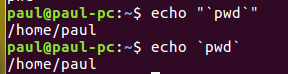
Linux实验三:shell程序设计: shell基础
实验目的: 进一步巩固shell程序设计语言基本语法,加深对所学知识理解。 实验要求 1. 四种变量的使用 2. 配置环境变量 3. 元字符和正则表达式 4. 引号 1. 本地变量 $ var1"hello Linux" //定义本地变量var1 $ read var2 //定义本地变量vae…...
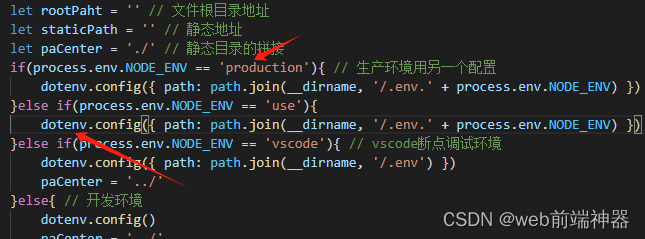
webpack环境变量的设置
现在虽然vite比较流行,但对于用node写后端来说,webpack倒是成了一个很好的打包工具,可以很好的保护后端的代码。所以这块的学习还是不能停下来,接下来我们来针对不同的环境做不同的设置写好笔记。 引用场景主要是针对服务器的各种…...
基于51单片机音乐盒设计( proteus仿真+程序+原理图+PCB+报告+讲解视频)
音乐盒 主要功能:仿真原理图PCB图程序设计:设计报告实物图资料清单(提供资料清单所有文件):资料下载链接: 基于51单片机音乐盒仿真设计( proteus仿真程序原理图PCB报告讲解视频) 仿真图proteus …...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
