【机器学习】算法性能评估常用指标总结
考虑一个二分问题,即将实例分成正类(positive)或负类(negative)。对一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被 预测成正类,即为真正类(True positive),如果实例是负类被预测成正类,称之为假正类(False positive)。相应地,如果实例是负类被预测成负类,称之为真负类(True negative),正类被预测成负类则为假负类(false negative)。
TP:正确肯定的数目;
FN:漏报,没有正确找到的匹配的数目;
FP:误报,给出的匹配是不正确的;
TN:正确拒绝的非匹配对数;
列联表如下表所示,1代表正类,0代表负类:
| 预测1 | 预测0 | |
| 实际1 | True Positive(TP) | False Negative(FN) |
| 实际0 | False Positive(FP) | True Negative(TN) |
1. TPR、FPR&TNR
从列联表引入两个新名词。其一是真正类率(true positive rate ,TPR), 计算公式为
TPR = TP / (TP + FN)
刻画的是分类器所识别出的 正实例占所有正实例的比例。
另外一个是负正类率(false positive rate, FPR),计算公式为
FPR = FP / (FP+ TN)
计算的是分类器错认为正类的负实例占所有负实例的比例。
还有一个真负类率(True Negative Rate,TNR),也称为specificity,计算公式为
TNR = TN /(FP+ TN) = 1 - FPR
2. 精确率Precision、召回率Recall和F1值
精确率(正确率)和召回率是广泛用于信息检索和统计学分类领域的两个度量值,用来评价结果的质量。其中精度是检索出相关文档数与检索出的文档总数的比率,衡量的是检索系统的查准率;召回率是指检索出的相关文档数和文档库中所有的相关文档数的比率,衡量的是检索系统的查全率。
一般来说,Precision就是检索出来的条目(比如:文档、网页等)有多少是准确的,Recall就是所有准确的条目有多少被检索出来了,两者的定义分别如下:
Precision = 提取出的正确信息条数 / 提取出的信息条数
Recall = 提取出的正确信息条数 / 样本中的信息条数
为了能够评价不同算法的优劣,在Precision和Recall的基础上提出了F1值的概念,来对Precision和Recall进行整体评价。F1的定义如下:
F1值 = 正确率 * 召回率 * 2 / (正确率+ 召回率)
不妨举这样一个例子:
某池塘有1400条鲤鱼,300只虾,300只鳖。现在以捕鲤鱼为目的。撒一大网,逮着了700条鲤鱼,200只虾,100只鳖。那么,这些指标分别如下:
正确率 = 700 / (700+ 200+100) = 70%
召回率 = 700 / 1400 = 50%
F1值 = 70% * 50% * 2 / (70%+50%) = 58.3%
不妨看看如果把池子里的所有的鲤鱼、虾和鳖都一网打尽,这些指标又有何变化:
正确率 = 1400 / (1400+ 300+ 300) = 70%
召回率 = 1400 / 1400 = 100%
F1值 = 70% * 100% * 2 / (70%+ 100%) = 82.35%
由此可见,正确率是评估捕获的成果中目标成果所占得比例;召回率,顾名思义,就是从关注领域中,召回目标类别的比例;而F值,则是综合这二者指标的评估指标,用于综合反映整体的指标。
当然希望检索结果Precision越高越好,同时Recall也越高越好,但事实上这两者在某些情况下有矛盾的。比如极端情况下,我们只搜索出了一个结果,且是准确的,那么Precision就是100%,但是Recall就很低;而如果我们把所有结果都返回,那么比如Recall是100%,但是Precision就会很低。因此在不同的场合中需要自己判断希望Precision比较高或是Recall比较高。如果是做实验研究,可以绘制Precision-Recall曲线来帮助分析。
3. 综合评价指标F-measure
Precision和Recall指标有时候会出现的矛盾的情况,这样就需要综合考虑他们,最常见的方法就是F-Measure(又称为F-Score)。
F-Measure是Precision和Recall加权调和平均:
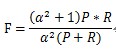
当参数α=1时,就是最常见的F1。因此,F1综合了P和R的结果,当F1较高时则能说明试验方法比较有效。
4. ROC曲线和AUC
4.1 为什么引入ROC曲线?
Motivation1:在一个二分类模型中,对于所得到的连续结果,假设已确定一个阀值,比如说 0.6,大于这个值的实例划归为正类,小于这个值则划到负类中。如果减小阀值,减到0.5,固然能识别出更多的正类,也就是提高了识别出的正例占所有正例 的比类,即TPR,但同时也将更多的负实例当作了正实例,即提高了FPR。为了形象化这一变化,引入ROC,ROC曲线可以用于评价一个分类器。
Motivation2:在类不平衡的情况下,如正样本90个,负样本10个,直接把所有样本分类为正样本,得到识别率为90%。但这显然是没有意义的。单纯根据Precision和Recall来衡量算法的优劣已经不能表征这种病态问题。
4.2 什么是ROC曲线?
ROC(Receiver Operating Characteristic)翻译为"接受者操作特性曲线"。曲线由两个变量1-specificity 和 Sensitivity绘制. 1-specificity=FPR,即负正类率。Sensitivity即是真正类率,TPR(True positive rate),反映了正类覆盖程度。这个组合以1-specificity对sensitivity,即是以代价(costs)对收益(benefits)。
此外,ROC曲线还可以用来计算“均值平均精度”(mean average precision),这是当你通过改变阈值来选择最好的结果时所得到的平均精度(PPV)。
为了更好地理解ROC曲线,我们使用具体的实例来说明:
如在医学诊断中,判断有病的样本。那么尽量把有病的揪出来是主要任务,也就是第一个指标TPR,要越高越好。而把没病的样本误诊为有病的,也就是第二个指标FPR,要越低越好。
不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的第一个指标应该会很高,但是第二个指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么第一个指标达到1,第二个指标也为1。
我们以FPR为横轴,TPR为纵轴,得到如下ROC空间。
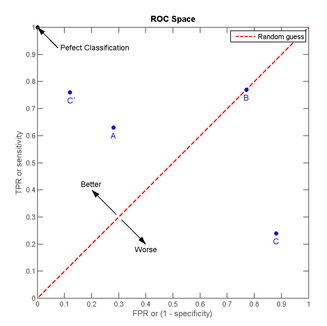
我们可以看出,左上角的点(TPR=1,FPR=0),为完美分类,也就是这个医生医术高明,诊断全对。点A(TPR>FPR),医生A的判断大体是正确的。中线上的点B(TPR=FPR),也就是医生B全都是蒙的,蒙对一半,蒙错一半;下半平面的点C(TPR<FPR),这个医生说你有病,那么你很可能没有病,医生C的话我们要反着听,为真庸医。上图中一个阈值,得到一个点。现在我们需要一个独立于阈值的评价指标来衡量这个医生的医术如何,也就是遍历所有的阈值,得到ROC曲线。
还是一开始的那幅图,假设如下就是某个医生的诊断统计图,直线代表阈值。我们遍历所有的阈值,能够在ROC平面上得到如下的ROC曲线。
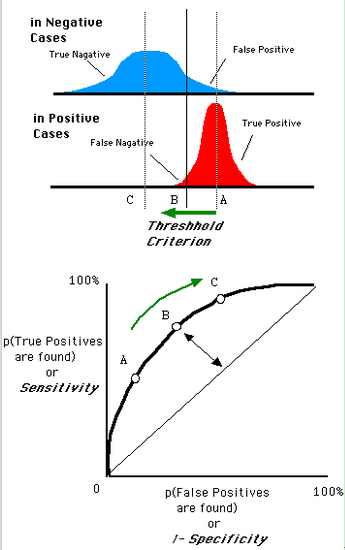
曲线距离左上角越近,证明分类器效果越好。
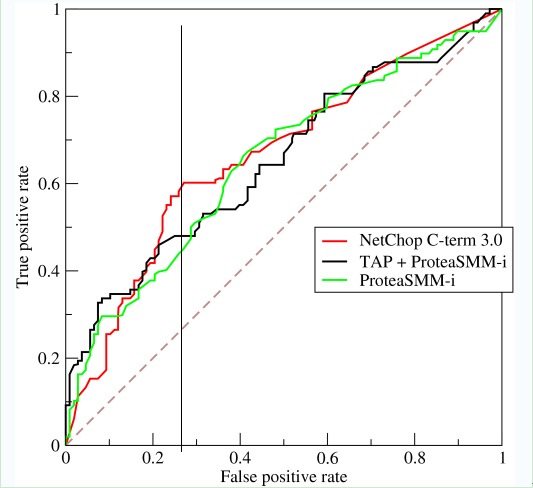
如上,是三条ROC曲线,在0.23处取一条直线。那么,在同样的低FPR=0.23的情况下,红色分类器得到更高的PTR。也就表明,ROC越往上,分类器效果越好。我们用一个标量值AUC来量化它。
4.3 什么是AUC?
AUC值为ROC曲线所覆盖的区域面积,显然,AUC越大,分类器分类效果越好。
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
AUC的物理意义:假设分类器的输出是样本属于正类的socre(置信度),则AUC的物理意义为,任取一对(正、负)样本,正样本的score大于负样本的score的概率。
4.4 怎样计算AUC?
第一种方法:AUC为ROC曲线下的面积,那我们直接计算面积可得。面积为一个个小的梯形面积之和。计算的精度与阈值的精度有关。
第二种方法:根据AUC的物理意义,我们计算正样本score大于负样本的score的概率。取NM(N为正样本数,M为负样本数)个二元组,比较score,最后得到AUC。时间复杂度为O(NM)。
第三种方法:与第二种方法相似,直接计算正样本score大于负样本的概率。我们首先把所有样本按照score排序,依次用rank表示他们,如最大score的样本,rank=n(n=N M),其次为n-1。那么对于正样本中rank最大的样本,rank_max,有M-1个其他正样本比他score小,那么就有(rank_max-1)-(M-1)个负样本比他score小。其次为(rank_second-1)-(M-2)。最后我们得到正样本大于负样本的概率为
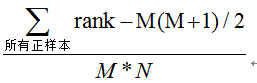
时间复杂度为O(N+M)。
相关文章:
【机器学习】算法性能评估常用指标总结
考虑一个二分问题,即将实例分成正类(positive)或负类(negative)。对一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被 预测成正类,即为真正类(True positive࿰…...

前端 JavaScript 与 HTML 怎么实现交互?
前端的交互性是通过JavaScript与HTML结合实现的。JavaScript作为一种脚本语言,可以嵌入HTML中,通过对DOM(文档对象模型)的操作,实现与用户的交互。以下将详细介绍前端JavaScript与HTML如何实现交互,包括事件…...
命令执行总结
之前做了一大堆的题目 都没有进行总结 现在来总结一下命令执行 我遇到的内容 这里我打算按照过滤进行总结 依据我做过的题目 过滤system 下面是一些常见的命令执行内容 system() passthru() exec() shell_exec() popen() proc_open() pcntl_exec() 反引号 同shell_exec() …...
)
机器学习——词向量模型(CBOW代码实现-未开始)
本来是不打算做这个CBOW代码案例的,想快马加鞭看看前馈神经网络 毕竟书都买好了 可是…可是…我看书的时候,感觉有点儿困难,哭的很大声… 感觉自己脑细胞可能无法这么快接受 要不,还是退而求个稍微难度没那么大的事,想…...

智慧海岛/海域方案:助力海洋空间智慧化、可视化管理
随着我国海洋经济的快速发展,海域海岛的安防技术也获得了进步。传统的安防监控模式已经满足不了海域海岛的远程监管需求。伴随着人工智能、边缘计算、大数据、通信传输技术、视频技术、物联网等信息化技术的发展,海岛海域在监管手段上,也迎来…...

Bin、Hex、ELF、AXF的区别
1.Bin Bin文件是最纯粹的二进制机器代码, 或者说是"顺序格式"。按照assembly code顺序翻译成binary machine code,内部没有地址标记。Bin是直接的内存映象表示,二进制文件大小即为文件所包含的数据的实际大小。 BIN文件就是直接的二进制文件&…...
IDEA安装教程
文章目录 1 下载IntelliJ IDEA2 安装3 IDEA配置4 创建项目 1 下载IntelliJ IDEA 官方网站上下载最新版本的IntelliJ IDEA。官方网站提供了两个版本:Community版和Ultimate版。 Community版是免费的,适用于个人和非商业用途。Ultimate版则需要付费购…...
DRF-项目-(1):构建纯净版的drf项目,不再使用django的后台管理,django的认证,django的session等功能,作为一个纯接口项目
项目的目录结构: -HeartFailure |-- apps |--user |--HeartFailure |-- static |--manage.py 一、django项目相关的 1、命令行中创建django项目 #1、切换到指定的虚拟环境中 workon my_drf#2、该虚拟环境已经安装好django和rest_framework了 django-admin startp…...

ubuntu 手动清理内存cache
/proc是一个虚拟文件系统,我们可以通过对它的读写操作来做为与kernel实体间进行通信的一种手段。也就是说可以通过修改/proc中的文件,来对当前kernel的行为做出调整。 那么我们可以通过调整/proc/sys/vm/drop_caches来释放内存。操作如下: …...
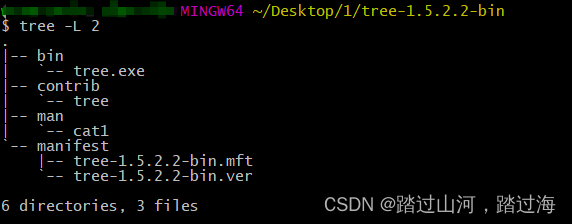
gitBash中如何使用Linux中的tree命令
文章目录 在gitBash中安装tree的目的如何安装安装完成,就可以直接完美适配Linux系统了 在gitBash中安装tree的目的 如下图,powershell虽然可以看做是window下的Linux系统,但是根本就不适配很多Linux中的命令 如何安装 tree.exe安装网址 下载 tree 命令的 二进制包…...

【鸿蒙应用ArkTS开发系列】- 灌水区,鸿蒙ArkTs开发有问题可以在该帖中反馈
大家好, 这是一篇水贴,给大家提供一个交流沟通鸿蒙开发遇到问题的地方。 新增新增这个文章呢,大家在开发使用ArkTS开发鸿蒙应用或者鸿蒙服务的时候,有遇到疑问或者问题,可以在本文章评论区提问,我看到了如果知道怎么…...
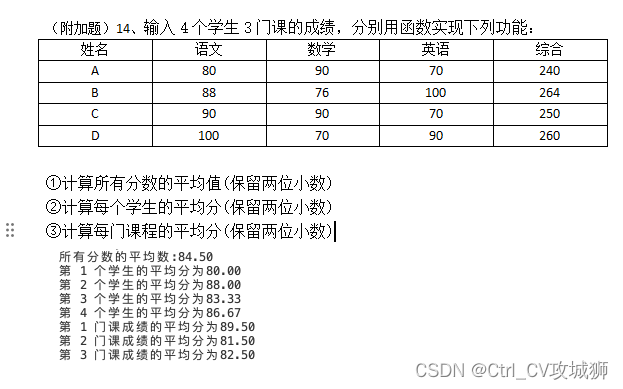
c语言习题1124
分别定义函数求圆的面积和周长。 写一个函数,分别求三个数当中的最大数。 写一个函数,计算输入n个数的乘积 一个判断素数的函数,在主函数输入一个整数,输出是否为素数的信息 写一个函数求n! ,利用该函数求1!2&…...

线段树---数据结构学习
线段树的教程可以参照线段树 这里推荐 https://oi-wiki.org/ 这个网站,数据结构讲的非常透。 线段树学了很多次忘了很多次,这次打算记录一下以后方便回顾(leetcode这类题遇见的不算特别多)。 样板例题 leltcode-307 #题目样板 class NumArray {private …...
linux基础5:linux进程1(冯诺依曼体系结构+os管理+进程状态1)
冯诺依曼体系结构os管理 一.冯诺依曼体系结构:1.简单介绍(准备一)2.场景:1.程序的运行:2.登录qq发送消息: 3.为什么需要内存:1.简单的引入:2.计算机存储体系:3.内存的意义…...
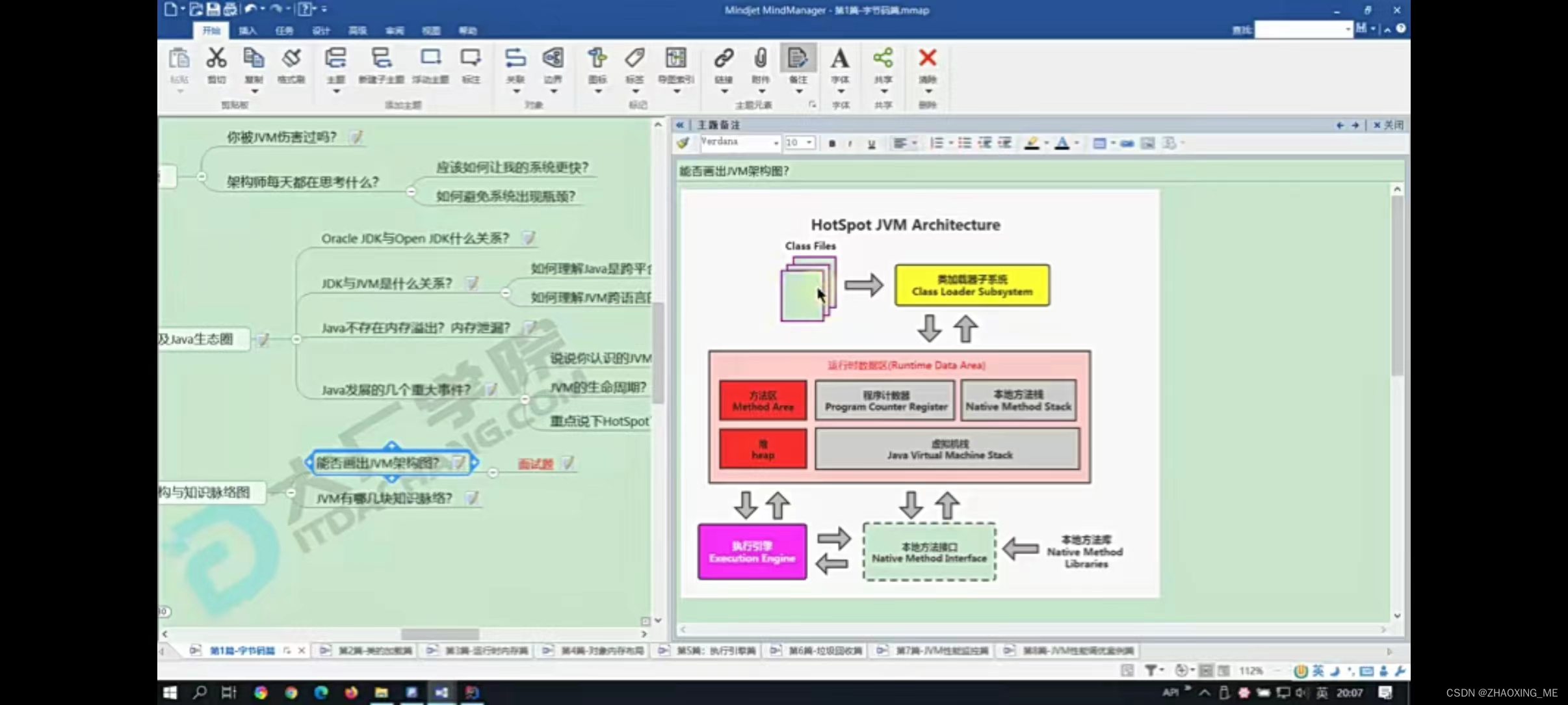
JVM-基础
jdk7及以前: 通过-XX:PermSize 来设置永久代初始分配空间,默认值是20.75m -XX:MaxPermSize来设定永久代最大可分配空间,32位是64m,64位是82m jdk8及之后: 通过-XX:MetaspaceSize 来设置永久代初始分配空间ÿ…...

Baidu Comate 基于百度文心一言的智能编码助手
本心、输入输出、结果 文章目录 Baidu Comate 基于百度文心一言的智能编码助手前言产品能力主要功能特性JetBrains IntelliJ IDEA 插件安装相关链接花有重开日,人无再少年实践是检验真理的唯一标准Baidu Comate 基于百度文心一言的智能编码助手 编辑:简简单单 Online zuozuo …...

基本微信小程序的图书馆座位管理系统
项目介绍 图书馆因有良好的学习氛围、大量的学习资源吸引大家前来学习,图书馆还未开馆就有大量的用户在门口排队等待,有限的座位与日益增加的自主学习者之间形成了供不应求的现象,再加上不了解图书馆的座位使用情况和恶意占座等现象,使得有限的学习座位越发紧张。本团队针对此…...
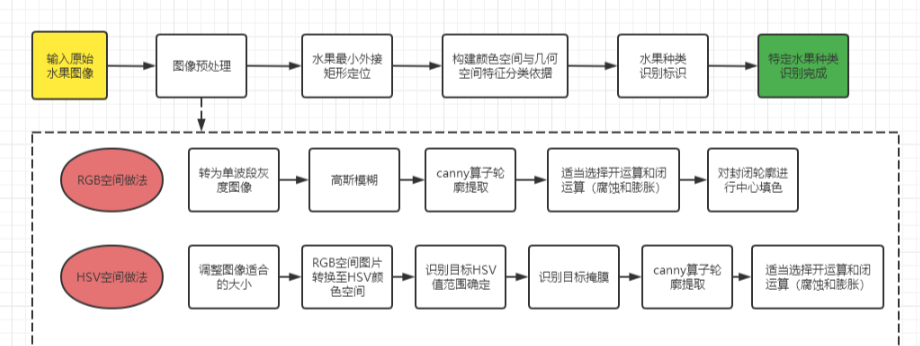
2023年亚太杯数学建模A题水果采摘机器人的图像识别功能(免费思路)
中国是世界上最大的苹果生产国,年产量约为 3500 万吨。同时,中国也是世界上最大的苹果出口国,世界上每两个苹果中就有一个出口到国。世界上每两个苹果中就有一个来自中国,中国出口的苹果占全球出口量的六分之一以上。来自中国。中…...

AWS CLI和EKSCTL的客户端设置
文章目录 小结过程安装AWS CLI安装EKSCTL在两个Kubernetes Cluster之间切换 参考 小结 在Linux环境中对AWS CLI和EKSCTL的客户端进行了设置。 过程 安装AWS CLI 使用以下指令安装: curl "https://awscli.amazonaws.com/awscli-exe-linux-x86_64.zip"…...

分组背包问题学习笔记 AcWing 9. 分组背包问题
原题 有 N� 组物品和一个容量是 V� 的背包。 每组物品有若干个,同一组内的物品最多只能选一个。 每件物品的体积是 vij���,价值是 wij���,其中 …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
