2304. 网格中的最小路径代价 : 从「图论最短路」过渡到「O(1) 空间的原地模拟」
题目描述
这是 LeetCode 上的 「2304. 网格中的最小路径代价」 ,难度为 「中等」。
Tag : 「最短路」、「图」、「模拟」、「序列 DP」、「动态规划」
给你一个下标从 0 开始的整数矩阵 grid,矩阵大小为 m x n,由从 0 到 的不同整数组成。
你可以在此矩阵中,从一个单元格移动到下一行的任何其他单元格。
如果你位于单元格 ,且满足 ,你可以移动到 , , ..., 中的任何一个单元格。注意: 在最后一行中的单元格不能触发移动。
每次可能的移动都需要付出对应的代价,代价用一个下标从 0 开始的二维数组 moveCost 表示,该数组大小为 ,其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。
grid 一条路径的代价是:所有路径经过的单元格的值之和加上所有移动的代价之和 。从第一行任意单元格出发,返回到达最后一行任意单元格的最小路径代价。
示例 1: 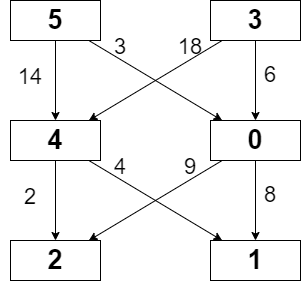
输入:grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
输出:17
解释:最小代价的路径是 5 -> 0 -> 1 。
- 路径途经单元格值之和 5 + 0 + 1 = 6 。
- 从 5 移动到 0 的代价为 3 。
- 从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。
示例 2:
输入:grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
输出:6
解释:
最小代价的路径是 2 -> 3 。
- 路径途经单元格值之和 2 + 3 = 5 。
- 从 2 移动到 3 的代价为 1 。
路径总代价为 5 + 1 = 6 。
提示:
-
-
-
-
grid由从0到m * n - 1的不同整数组成 -
-
-
建新图 + 建虚拟点 + 堆优化 Dijkstra
❝注意:可以直接使用解法二的方法,但先认真看完本做法,再去看解法二,会有相当丝滑的体验。
❞
每次移动,「实际路径权值 = 经过边的权值 + 目的地的权值」。
利用原图,构建新图:「每个单元格视为一个点,除最后一行外,每个点对下一行的所有点连一条有向边,边权 = 原图中该边的权值 + 原图中该目的地的权值」。
分析新图中的点边数量:
-
点:共 个点,数量为 -
边:不算最后一行,共 个点,这些点与下一行的每个点均有一条有向边,合计 条边,数量为
原问题转换为:求点 到 的最短路,其中点 所在位置为第 行,点 所在位置为第 行。
这似乎是一个「多源汇最短路」问题?但求解多源汇最短路的 Floyd 算法是 的,会超时。
实际上,我们也并不真的关心图中任意点之间的最短路,仅仅关心第一行到最后一行的最短路。
因此,「我们可通过建立“虚拟源点”和“虚拟汇点”的方式,来将“多源汇最短路”问题转换为“单源最短路”问题。」
具体的,我们创建一个“虚拟源点”,该点向所有第一行的点连权值为 的有向边;同时创建一个“虚拟汇点”,最后一行的所有点向该点连权值为 的有向边。
问题进一步转化为:求“虚拟源点”到“虚拟汇点”的最短路。
至此,我们通过 「建新图 -> 创建虚拟源汇点(转换为单源最短路)-> 套用单源最短路算法」 解决本题。
将新图中点的数量记为 ,边数记为 ,朴素 Dijkstra 复杂度为 ,堆优化的 Dijkstra 的复杂度为 ,当 (相对稀疏)时,优先使用堆优化 Dijkstra。
Java 代码:
class Solution {
int N = 50 * 50 + 2, M = 50 * 50 * 50, idx = 0, n;
int[] he = new int[N], e = new int[M], ne = new int[M], w = new int[M];
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = he[a];
w[idx] = c;
he[a] = idx++;
}
public int minPathCost(int[][] grid, int[][] moveCost) {
int N = grid.length, M = grid[0].length;
int S = N * M, T = S + 1;
n = N * M + 2;
Arrays.fill(he, -1);
//「虚拟源点」向「第一行」进行连边
for (int i = 0; i < M; i++) add(S, grid[0][i], grid[0][i]);
// 转换原图
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < M; j++) {
int a = grid[i][j];
for (int k = 0; k < M; k++) {
int b = grid[i + 1][k];
add(a, b, moveCost[a][k] + b);
}
}
}
//「最后一行」向「虚拟汇点」进行连边
for (int i = 0; i < M; i++) add(grid[N - 1][i], T, 0);
// 最短路
int[] dist = dijkstra(S);
return dist[T];
}
int[] dijkstra(int x) {
// 起始先将所有的点标记为「未更新」和「距离为正无穷」
int[] dist = new int[n];
Arrays.fill(dist, 0x3f3f3f3f);
boolean[] vis = new boolean[n];
dist[x] = 0;
// 使用「优先队列」存储所有可用于更新的点
// 以 (点编号, 到起点的距离) 进行存储,优先弹出「最短距离」较小的点
PriorityQueue<int[]> q = new PriorityQueue<>((a,b)->a[1]-b[1]);
q.add(new int[]{x, 0});
while (!q.isEmpty()) {
// 每次从「优先队列」中弹出
int[] poll = q.poll();
int u = poll[0], step = poll[1];
// 如果弹出的点被标记「已更新」,则跳过
if (vis[u]) continue;
// 标记该点「已更新」,并使用该点更新其他点的「最短距离」
vis[u] = true;
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] <= dist[u] + w[i]) continue;
dist[j] = dist[u] + w[i];
q.add(new int[]{j, dist[j]});
}
}
return dist;
}
}
C++ 代码:
class Solution {
public:
static const int N = 50 * 50 + 2, M = 50 * 50 * 50;
int he[N], e[M], ne[M], w[M], idx, n, INF = 0x3f3f3f3f;
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = he[a];
w[idx] = c;
he[a] = idx++;
}
int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
int N = grid.size(), M = grid[0].size();
int S = N * M, T = S + 1;
n = N * M + 2;
fill(he, he + n, -1);
//「虚拟源点」向「第一行」进行连边
for (int i = 0; i < M; i++) add(S, grid[0][i], grid[0][i]);
// 转换原图
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < M; j++) {
int a = grid[i][j];
for (int k = 0; k < M; k++) {
int b = grid[i + 1][k];
add(a, b, moveCost[a][k] + b);
}
}
}
//「最后一行」向「虚拟汇点」进行连边
for (int i = 0; i < M; i++) add(grid[N - 1][i], T, 0);
// 最短路
vector<int> dist = dijkstra(S);
return dist[T];
}
vector<int> dijkstra(int x) {
vector<int> dist(n, 0x3f3f3f3f);
vector<bool> vis(n, false);
dist[x] = 0;
// 使用「优先队列」存储所有可用于更新的点
// 以 (到起点的距离, 点编号) 进行存储,优先弹出「最短距离」较小的点
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
q.push({0, x});
while (!q.empty()) {
// 每次从「优先队列」中弹出
auto [step, u] = q.top();
q.pop();
// 如果弹出的点被标记「已更新」,则跳过
if (vis[u]) continue;
// 标记该点「已更新」,并使用该点更新其他点的「最短距离」
vis[u] = true;
for (int i = he[u]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] <= dist[u] + w[i]) continue;
dist[j] = dist[u] + w[i];
q.push({dist[j], j});
}
}
return dist;
}
};
Python 代码:
import heapq
class Solution:
def minPathCost(self, grid, moveCost):
N, M = len(grid), len(grid[0])
S, T = N * M, N * M + 1
n = N * M + 2
he = [-1] * n
e, ne, w = [-1] * (50 * 50 * 50), [-1] * (50 * 50 * 50), [-1] * (50 * 50 * 50)
idx = 0
def add(a, b, c):
nonlocal idx
e[idx] = b
ne[idx] = he[a]
w[idx] = c
he[a] = idx
idx += 1
def dijkstra(x):
dist = [float('inf')] * n
vis = [False] * n
dist[x] = 0
# 使用「优先队列」存储所有可用于更新的点
# 以 (到起点的距离, 点编号) 进行存储,优先弹出「最短距离」较小的点
q = [(0, x)]
heapq.heapify(q)
while q:
# 每次从「优先队列」中弹出
step, u = heapq.heappop(q)
# 如果弹出的点被标记「已更新」,则跳过
if vis[u]: continue
# 标记该点「已更新」,并使用该点更新其他点的「最短距离」
vis[u] = True
i = he[u]
while i != -1:
j, c = e[i], w[i]
i = ne[i]
if dist[j] <= dist[u] + c: continue
dist[j] = dist[u] + c
heapq.heappush(q, (dist[j], j))
return dist
#「虚拟源点」向「第一行」进行连边
for i in range(M):
add(S, grid[0][i], grid[0][i])
# 转换原图
for i in range(N - 1):
for j in range(M):
a = grid[i][j]
for k in range(M):
b = grid[i + 1][k]
add(a, b, moveCost[a][k] + b)
#「最后一行」向「虚拟汇点」进行连边
for i in range(M):
add(grid[N - 1][i], T, 0)
# 最短路
dist = dijkstra(S)
return dist[T]
-
时间复杂度: ,其中 为新图中的点数 , 为新图中的边数 -
空间复杂度:
堆优化 Dijkstra
什么?你说你实在不想建新图,也不想搞什么虚拟点,就想用你心爱的 BFS 来做?!
我懂你意思,但那不叫 BFS。
只是将「建新图」和「建虚拟点」的过程省掉,仍需要使用优先队列(堆)来每次取出当前“路径代价最小”的点来进行扩充,执行过程仍为堆优化 Dijkstra 的核心操作。
尤其所谓“省掉” 建新图 和 建虚拟点,真就字面上的“省掉”,并非不存在,因为两种做法思路是完全一致的。可简单列举「本解法」与「解法一」的对应关系:
-
起始往队列放入首行元素,对应了解法一的“建立虚拟源点”过程; -
从队列中取元素出来扩充时,若当前元素所在行是最后一行时,用当前路径代价来更新答案,对应了解法一的“建立虚拟汇点”过程; -
扩充时直接遍历列(即下一行的所有点),对应的解法一的“用原图边建新图”的过程。
Java 代码:
class Solution {
public int minPathCost(int[][] grid, int[][] moveCost) {
int m = grid.length, n = grid[0].length, INF = 0x3f3f3f3f, ans = INF;
int[][] dist = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) dist[i][j] = INF;
}
PriorityQueue<int[]> d = new PriorityQueue<>((a,b)->a[2]-b[2]);
for (int i = 0; i < n; i++) {
d.add(new int[]{0, i, grid[0][i]});
dist[0][i] = grid[0][i];
}
while (!d.isEmpty()) {
int[] info = d.poll();
int x = info[0], y = info[1], cur = info[2];
if (x == m - 1) {
ans = Math.min(ans, cur);
continue;
}
for (int i = 0; i < n; i++) {
int step = moveCost[grid[x][y]][i], ne = grid[x + 1][i];
int tot = cur + step + ne;
if (tot >= ans || dist[x + 1][i] <= tot) continue;
dist[x + 1][i] = tot;
d.add(new int[]{x + 1, i, tot});
}
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
int m = grid.size(), n = grid[0].size(), INF = 0x3f3f3f3f, ans = INF;
vector<vector<int>> dist(m, vector<int>(n, INF));
priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;
for (int i = 0; i < n; i++) {
pq.push({0, i, grid[0][i]});
dist[0][i] = grid[0][i];
}
while (!pq.empty()) {
vector<int> info = pq.top();
pq.pop();
int x = info[0], y = info[1], cur = info[2];
if (x == m - 1) {
ans = min(ans, cur);
continue;
}
for (int i = 0; i < n; i++) {
int step = moveCost[grid[x][y]][i], ne = grid[x + 1][i];
int tot = cur + step + ne;
if (tot >= ans || dist[x + 1][i] <= tot) continue;
dist[x + 1][i] = tot;
pq.push({x + 1, i, tot});
}
}
return ans;
}
};
Python 代码:
class Solution:
def minPathCost(self, grid, moveCost):
m, n, INF = len(grid), len(grid[0]), float('inf')
ans = INF
dist = [[INF] * n for _ in range(m)]
for i in range(n):
dist[0][i] = grid[0][i]
pq = [(0, i, grid[0][i]) for i in range(n)]
while pq:
x, y, cur = heapq.heappop(pq)
if x == m - 1:
ans = min(ans, cur)
continue
for i in range(n):
step, ne = moveCost[grid[x][y]][i], grid[x + 1][i]
tot = cur + step + ne
if tot >= ans or dist[x + 1][i] <= tot: continue
dist[x + 1][i] = tot
heapq.heappush(pq, (x + 1, i, tot))
return ans
-
时间复杂度: ,其中 为新图中的点数 , 为新图中的边数 -
空间复杂度:
原地模拟
什么?你说你连图论的方法都不想用,想就着题意做一遍?
可以。甚至当你调整更新方向,还能利用已有的 grid,实现原地模拟。
具体的,我们将“从上往下走”调整为“从下往上走”,这样可以确保当我们使用底下一行 来更新当前行 时,所用到的 不会被覆盖。
Java 代码:
class Solution {
public int minPathCost(int[][] grid, int[][] moveCost) {
int m = grid.length, n = grid[0].length, INF = 0x3f3f3f3f, ans = INF;
for (int i = m - 2; i >= 0; i--) {
for (int j = 0; j < n; j++) {
int cur = INF;
for (int k = 0; k < n; k++) cur = Math.min(cur, grid[i + 1][k] + moveCost[grid[i][j]][k]);
grid[i][j] += cur;
}
}
for (int i = 0; i < n; i++) ans = Math.min(ans, grid[0][i]);
return ans;
}
}
C++ 代码:
class Solution {
public:
int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
int m = grid.size(), n = grid[0].size(), INF = INT_MAX, ans = INF;
for (int i = m - 2; i >= 0; i--) {
for (int j = 0; j < n; j++) {
int cur = INF;
for (int k = 0; k < n; k++) cur = min(cur, grid[i + 1][k] + moveCost[grid[i][j]][k]);
grid[i][j] += cur;
}
}
for (int i = 0; i < n; i++) ans = min(ans, grid[0][i]);
return ans;
}
};
Python 代码:
class Solution:
def minPathCost(self, grid, moveCost):
m, n = len(grid), len(grid[0])
for i in range(m - 2, -1, -1):
for j in range(n):
grid[i][j] += min([grid[i + 1][k] + moveCost[grid[i][j]][k] for k in range(n)])
return min([grid[0][i] for i in range(n)])
TypeScript 代码:
function minPathCost(grid: number[][], moveCost: number[][]): number {
let m = grid.length, n = grid[0].length, INF = 0x3f3f3f3f, ans = INF;
for (let i = m - 2; i >= 0; i--) {
for (let j = 0; j < n; j++) {
let cur = INF;
for (let k = 0; k < n; k++) cur = Math.min(cur, grid[i + 1][k] + moveCost[grid[i][j]][k]);
grid[i][j] += cur;
}
}
for (let i = 0; i < n; i++) ans = Math.min(ans, grid[0][i]);
return ans;
};
-
时间复杂度: ,其中 和 分别代表给定 grid的长宽 -
空间复杂度:
最后
这是我们「刷穿 LeetCode」系列文章的第 No.2304 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
相关文章:

2304. 网格中的最小路径代价 : 从「图论最短路」过渡到「O(1) 空间的原地模拟」
题目描述 这是 LeetCode 上的 「2304. 网格中的最小路径代价」 ,难度为 「中等」。 Tag : 「最短路」、「图」、「模拟」、「序列 DP」、「动态规划」 给你一个下标从 0 开始的整数矩阵 grid,矩阵大小为 m x n,由从 0 到 的不同整数组成。 你…...
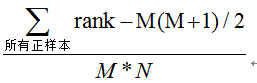
【机器学习】算法性能评估常用指标总结
考虑一个二分问题,即将实例分成正类(positive)或负类(negative)。对一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被 预测成正类,即为真正类(True positive࿰…...

前端 JavaScript 与 HTML 怎么实现交互?
前端的交互性是通过JavaScript与HTML结合实现的。JavaScript作为一种脚本语言,可以嵌入HTML中,通过对DOM(文档对象模型)的操作,实现与用户的交互。以下将详细介绍前端JavaScript与HTML如何实现交互,包括事件…...
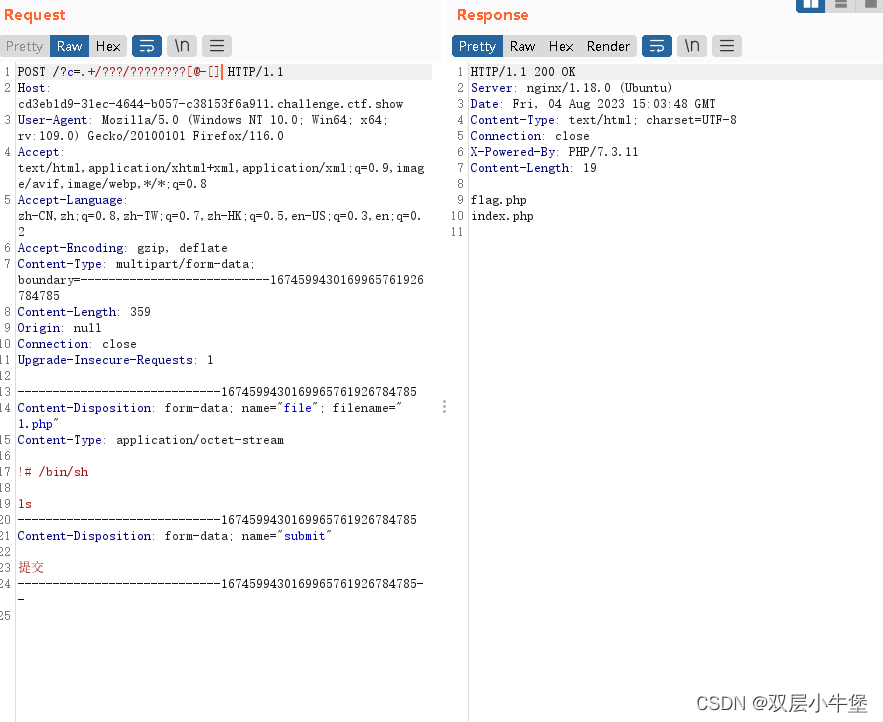
命令执行总结
之前做了一大堆的题目 都没有进行总结 现在来总结一下命令执行 我遇到的内容 这里我打算按照过滤进行总结 依据我做过的题目 过滤system 下面是一些常见的命令执行内容 system() passthru() exec() shell_exec() popen() proc_open() pcntl_exec() 反引号 同shell_exec() …...
)
机器学习——词向量模型(CBOW代码实现-未开始)
本来是不打算做这个CBOW代码案例的,想快马加鞭看看前馈神经网络 毕竟书都买好了 可是…可是…我看书的时候,感觉有点儿困难,哭的很大声… 感觉自己脑细胞可能无法这么快接受 要不,还是退而求个稍微难度没那么大的事,想…...

智慧海岛/海域方案:助力海洋空间智慧化、可视化管理
随着我国海洋经济的快速发展,海域海岛的安防技术也获得了进步。传统的安防监控模式已经满足不了海域海岛的远程监管需求。伴随着人工智能、边缘计算、大数据、通信传输技术、视频技术、物联网等信息化技术的发展,海岛海域在监管手段上,也迎来…...

Bin、Hex、ELF、AXF的区别
1.Bin Bin文件是最纯粹的二进制机器代码, 或者说是"顺序格式"。按照assembly code顺序翻译成binary machine code,内部没有地址标记。Bin是直接的内存映象表示,二进制文件大小即为文件所包含的数据的实际大小。 BIN文件就是直接的二进制文件&…...
IDEA安装教程
文章目录 1 下载IntelliJ IDEA2 安装3 IDEA配置4 创建项目 1 下载IntelliJ IDEA 官方网站上下载最新版本的IntelliJ IDEA。官方网站提供了两个版本:Community版和Ultimate版。 Community版是免费的,适用于个人和非商业用途。Ultimate版则需要付费购…...
DRF-项目-(1):构建纯净版的drf项目,不再使用django的后台管理,django的认证,django的session等功能,作为一个纯接口项目
项目的目录结构: -HeartFailure |-- apps |--user |--HeartFailure |-- static |--manage.py 一、django项目相关的 1、命令行中创建django项目 #1、切换到指定的虚拟环境中 workon my_drf#2、该虚拟环境已经安装好django和rest_framework了 django-admin startp…...

ubuntu 手动清理内存cache
/proc是一个虚拟文件系统,我们可以通过对它的读写操作来做为与kernel实体间进行通信的一种手段。也就是说可以通过修改/proc中的文件,来对当前kernel的行为做出调整。 那么我们可以通过调整/proc/sys/vm/drop_caches来释放内存。操作如下: …...
gitBash中如何使用Linux中的tree命令
文章目录 在gitBash中安装tree的目的如何安装安装完成,就可以直接完美适配Linux系统了 在gitBash中安装tree的目的 如下图,powershell虽然可以看做是window下的Linux系统,但是根本就不适配很多Linux中的命令 如何安装 tree.exe安装网址 下载 tree 命令的 二进制包…...

【鸿蒙应用ArkTS开发系列】- 灌水区,鸿蒙ArkTs开发有问题可以在该帖中反馈
大家好, 这是一篇水贴,给大家提供一个交流沟通鸿蒙开发遇到问题的地方。 新增新增这个文章呢,大家在开发使用ArkTS开发鸿蒙应用或者鸿蒙服务的时候,有遇到疑问或者问题,可以在本文章评论区提问,我看到了如果知道怎么…...
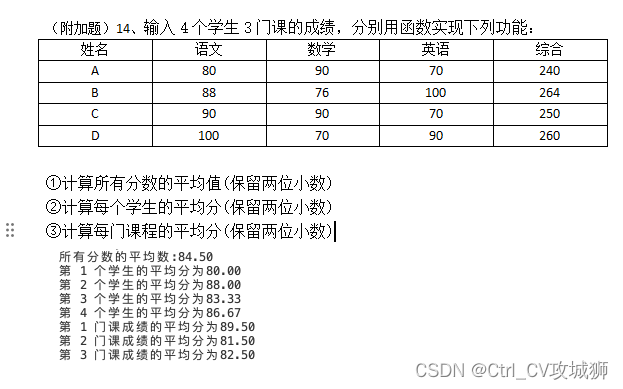
c语言习题1124
分别定义函数求圆的面积和周长。 写一个函数,分别求三个数当中的最大数。 写一个函数,计算输入n个数的乘积 一个判断素数的函数,在主函数输入一个整数,输出是否为素数的信息 写一个函数求n! ,利用该函数求1!2&…...

线段树---数据结构学习
线段树的教程可以参照线段树 这里推荐 https://oi-wiki.org/ 这个网站,数据结构讲的非常透。 线段树学了很多次忘了很多次,这次打算记录一下以后方便回顾(leetcode这类题遇见的不算特别多)。 样板例题 leltcode-307 #题目样板 class NumArray {private …...
linux基础5:linux进程1(冯诺依曼体系结构+os管理+进程状态1)
冯诺依曼体系结构os管理 一.冯诺依曼体系结构:1.简单介绍(准备一)2.场景:1.程序的运行:2.登录qq发送消息: 3.为什么需要内存:1.简单的引入:2.计算机存储体系:3.内存的意义…...
JVM-基础
jdk7及以前: 通过-XX:PermSize 来设置永久代初始分配空间,默认值是20.75m -XX:MaxPermSize来设定永久代最大可分配空间,32位是64m,64位是82m jdk8及之后: 通过-XX:MetaspaceSize 来设置永久代初始分配空间ÿ…...

Baidu Comate 基于百度文心一言的智能编码助手
本心、输入输出、结果 文章目录 Baidu Comate 基于百度文心一言的智能编码助手前言产品能力主要功能特性JetBrains IntelliJ IDEA 插件安装相关链接花有重开日,人无再少年实践是检验真理的唯一标准Baidu Comate 基于百度文心一言的智能编码助手 编辑:简简单单 Online zuozuo …...

基本微信小程序的图书馆座位管理系统
项目介绍 图书馆因有良好的学习氛围、大量的学习资源吸引大家前来学习,图书馆还未开馆就有大量的用户在门口排队等待,有限的座位与日益增加的自主学习者之间形成了供不应求的现象,再加上不了解图书馆的座位使用情况和恶意占座等现象,使得有限的学习座位越发紧张。本团队针对此…...
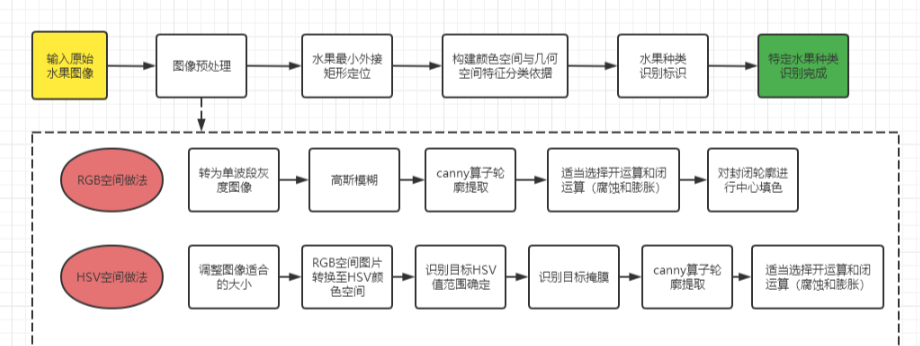
2023年亚太杯数学建模A题水果采摘机器人的图像识别功能(免费思路)
中国是世界上最大的苹果生产国,年产量约为 3500 万吨。同时,中国也是世界上最大的苹果出口国,世界上每两个苹果中就有一个出口到国。世界上每两个苹果中就有一个来自中国,中国出口的苹果占全球出口量的六分之一以上。来自中国。中…...

AWS CLI和EKSCTL的客户端设置
文章目录 小结过程安装AWS CLI安装EKSCTL在两个Kubernetes Cluster之间切换 参考 小结 在Linux环境中对AWS CLI和EKSCTL的客户端进行了设置。 过程 安装AWS CLI 使用以下指令安装: curl "https://awscli.amazonaws.com/awscli-exe-linux-x86_64.zip"…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
