UVa 12569 Planning mobile robot on Tree (EASY Version) 树上机器人规划(简单版) BFS 二进制
题目链接:Planning mobile robot on Tree (EASY Version)
题目描述:
给定一棵树,树上有一个位置存在一个机器人,其他mmm个位置存在石头,保证初始状态一个结点最多一个物体(一个石头或者一个机器人或者为空),你的任务是用尽量少的操作将机器人移动到目标结点,如果不能到达输出−1-1−1,如果可以输出路径,如果存在多条最小路径输出任意一条即可。你可以执行的操作如下:
- 将一个机器人移动到与其相邻的某个空结点上。
- 将一个石头移动到与其相邻的某个空结点上。
题解:
本题可以使用BFSBFSBFS来做,由于最多有151515个结点,我们可以用一个151515位的二进制来表示某个结点是否存在石头或者机器人,同时我们可以用一个变量来记录某个状态的机器人的位置。那么我们只需要进行简单的BFSBFSBFS即可找到最短路径:
dis[s][i]dis[s][i]dis[s][i]表示当前状态为sss,机器人的位置在jjj时需要的移动次数。那么移动的操作(u,v)(u,v)(u,v)可行的条件是:
- sss中uuu位置有东西
- u,vu,vu,v之间存在边
- sss中vvv位置没有东西(一个不能存在两个物体)
如何进行路径点的输出?路径的输出有很多种方法,我采用的是记录每个状态的上一次的状态,然后通过递归来输出状态(这里也可以使用一个栈来输出,只要满足先进后出即可),当前的状态与转移到当前状态的标记不同的结点就是发生了移动操作的结点。
代码:
#include <bits/stdc++.h>const int MAXN = 15;
const int MAXM = MAXN - 2;using namespace std;int dis[1 << 16][MAXN];
int haveStone[MAXN], head[MAXN];
int T, n, m, s, t, stonePos, caseID, ecnt, u, v;typedef pair<int, int> State;State ans;
State pre[1 << 16][MAXN];struct EdgeList
{int to;int nex;
}es[MAXN << 1];void addEdge(int u, int v)
{es[ecnt].to = v;es[ecnt].nex = head[u];head[u] = ecnt++;
}State getInitialState()
{int status = 0;for (int i = 0; i < n; i++) { status |= (int)haveStone[i] << i; }status |= 1 << s;return make_pair(status, s);
}void bfs()
{queue<State> q;State &&initialState = getInitialState();dis[initialState.first][initialState.second] = 0;q.push(initialState);State now, newState;while (!q.empty()) {now = q.front();q.pop();if (now.second == t) {ans = now;return;}for (int u = 0; u < n; u++) {if (((1 << u) & now.first) == 0) { continue; }for (int i = head[u]; i != -1; i = es[i].nex) {int v = es[i].to; // 进行u->v的移动if (((1 << v) & now.first) != 0) { continue; }newState.first = now.first ^ (1 << u) ^ (1 << v);if (u == now.second) { newState.second = v; }else { newState.second = now.second; }if (dis[newState.first][newState.second] != -1) { continue; }dis[newState.first][newState.second] = dis[now.first][now.second] + 1;pre[newState.first][newState.second] = now;q.push(newState);}}}
}void print(State &now)
{if (now.second == -1 || pre[now.first][now.second].second == -1) { return; }print(pre[now.first][now.second]);for (int i = 0; i < n; i++) {if ((now.first & (1 << i)) == 0 && (pre[now.first][now.second].first & (1 << i)) != 0) {u = i + 1;}if ((now.first & (1 << i)) != 0 && (pre[now.first][now.second].first & (1 << i)) == 0) {v = i + 1;}}cout << u << " " << v << endl;
}void printPath()
{caseID++;cout << "Case " << caseID << ": ";if (ans.second == -1) {cout << "-1" << endl;return;}cout << dis[ans.first][ans.second] << endl;print(ans);cout << endl;
}void init()
{ecnt = 0;ans.second = -1;memset(pre, -1, sizeof(pre));memset(dis, -1, sizeof(dis));memset(head, -1, sizeof(head));memset(haveStone, 0, sizeof(haveStone));
}int main()
{cin >> T;while (T--) {init();cin >> n >> m >> s >> t; s--; t--;for (int i = 0; i < m; i++) {cin >> stonePos; stonePos--;haveStone[stonePos] = true;}for (int i = 0; i < n - 1; i++) {cin >> u >> v; u--; v--;addEdge(u, v); addEdge(v, u);}bfs();printPath();}return 0;
}相关文章:
 树上机器人规划(简单版) BFS 二进制)
UVa 12569 Planning mobile robot on Tree (EASY Version) 树上机器人规划(简单版) BFS 二进制
题目链接:Planning mobile robot on Tree (EASY Version) 题目描述: 给定一棵树,树上有一个位置存在一个机器人,其他mmm个位置存在石头,保证初始状态一个结点最多一个物体(一个石头或者一个机器人或者为空…...
intel的集成显卡(intel(r) uhd graphics) 配置stable diffusion
由于很多商务本没有独立显卡,只有Intel的集成显卡,在配置安装stable diffusion 时候需要特殊对待,参考不少帖子,各取部分现稍加整合。整体思路分两个部分:第一步是先配置环境,主要是安装Anaconda Pytorch&…...

【数据库的基础知识(2)】
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Docker部署实战
文章目录Docker部署应用准备制作容器镜像启动容器上传镜像docker exec数据卷(Volume)声明原理实践Docker部署 应用准备 这一次,我们来用 Docker 部署一个用 Python 编写的 Web 应用。这个应用的代码部分(app.py)非常…...

RestTemplate 相关使用
RestTemplate介绍简单接口调用(getForObject)添加 Header 和 Cookie(exchange)介绍 在项目中,当我们需要远程调用一个 HTTP 接口时,我们经常会用到 RestTemplate 这个类。这个类是 Spring 框架提供的一个工…...
新手小白亚马逊注册最全教程在此
自从龙哥出了Walmart注册教程后,立刻看到私信有兄弟问这个亚马逊的注册。亚马逊是跨境电商的鼻祖,资源和流量是无容置疑的。作为一个重产品,轻店铺的平台,是比较看中客户体验的,要求卖家要有好的资源。而且亚马逊有强大…...
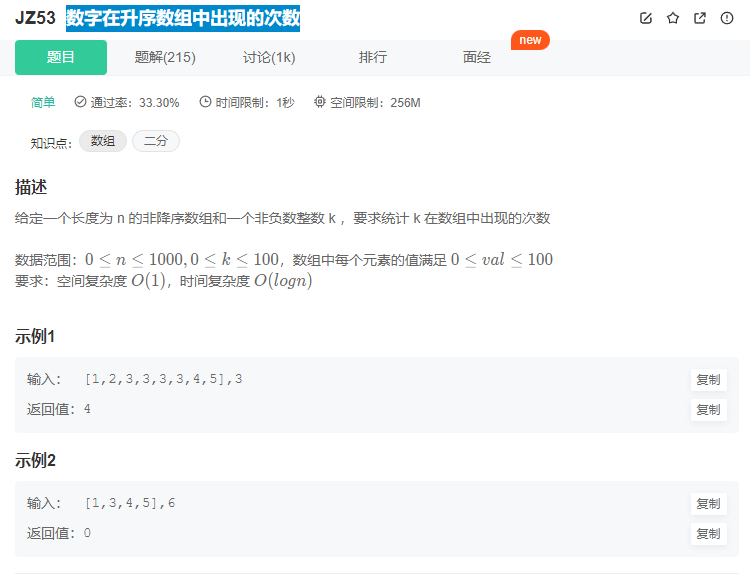
二分查找重复情况 找最左边或最右边的位置下标
目录二分找最左边二分找最右边综合应用(剑指offer)二分找最左边 核心思想: 先mid (lr)/2每次向左取整; 然后命中target的时候,右边界逼近到mid; 因为每次mid向左取整,mid命中target时l代替mid位置,则循环迭代最后会卡出重复数字最左侧的位置…...
智慧扫码点餐系统源码
智慧餐厅扫码点餐小程序系统源码 1. 开发语言:JAVA 2. 数据库:MySQL 3. 原生小程序 4. Saas 模式 5. 带调试部署视频 6、总后台管理端商家端门店端小程序用户端 智慧扫码点餐系统支持多店铺运营,单店铺运营以及连锁店铺运营。系统功能支…...
)
分布式环境并发场景下,如何操作抢红包(或者减少库存)
文章目录简介思考lua 对 redis 的原子操作其他解决方式一些问题简介 在分布式场景高并发环境中,无论是抢红包还是减库存,其实本质上都是如何处理高并发中共享资源的问题,保证高并发资源分配的安全性 相互学习,如有错误还请指正&…...

明星的孩子也在做的感统训练,真的有用吗?
林志颖曾经在社交网站晒过带他儿子“模拟过山车”的视频。孩子大脑前庭受到适当的刺激,可以有效地锻炼前庭平衡感。 除此之外,还能看见地上的感统教具:过河石、平衡桥,看来明星老爸在陪孩子做感统游戏的日常一点也不含糊。 其实在…...
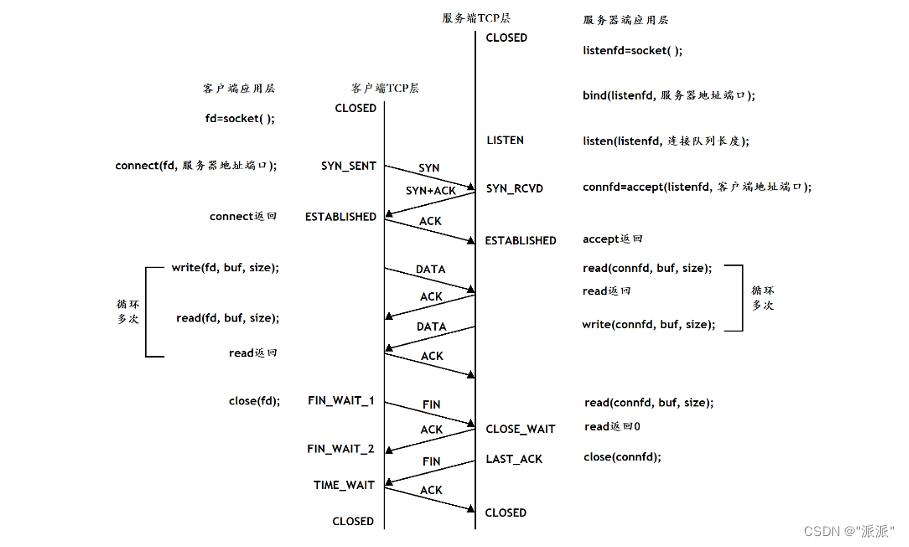
守护进程与TCP通讯
目录 一.守护进程 1.1进程组与会画 1.2守护进程 二.创建守护进程 setsid函数: 三. TCP通讯流程 3.1三次握手: 3.2 数据传输的过程 3.3四次挥手 一.守护进程 1.1进程组与会画 进程组:进程组由一个进程或者多个进程组成,每…...
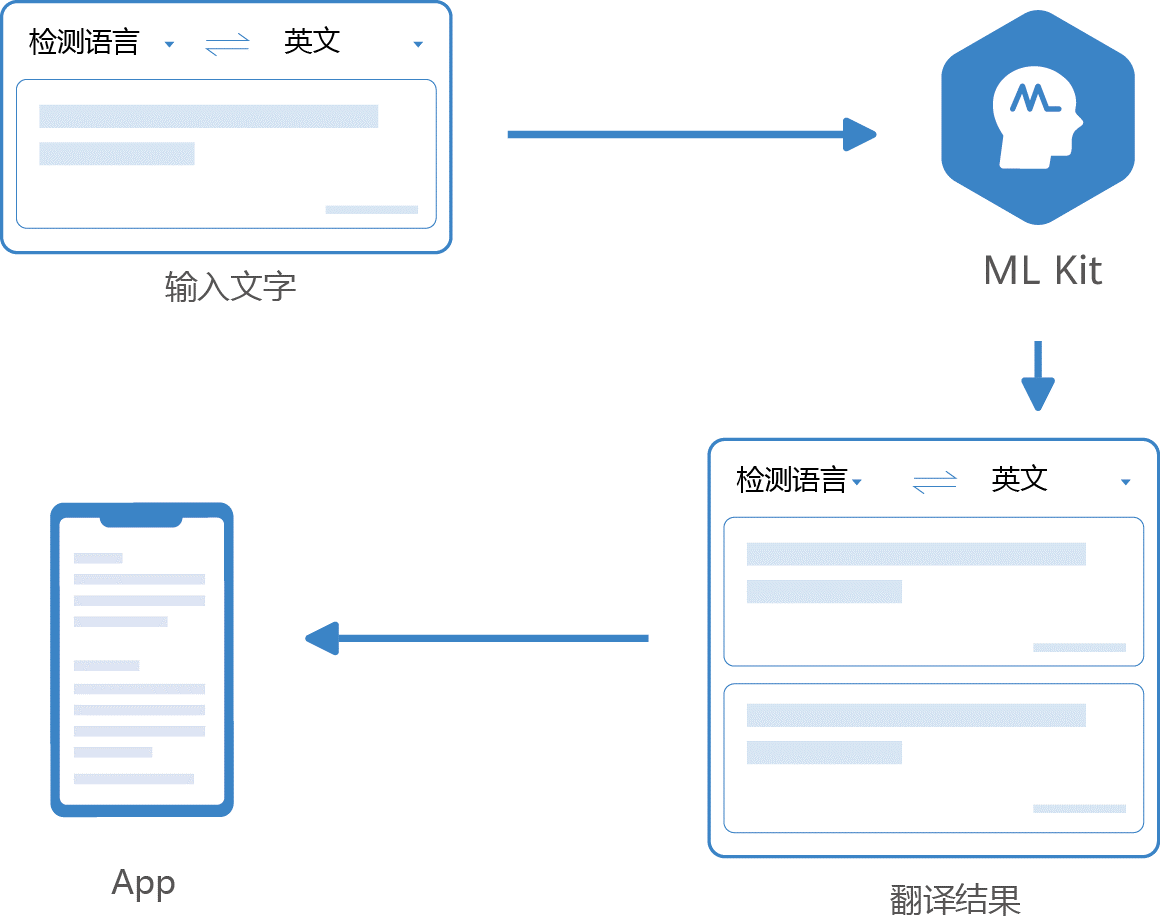
在线文本翻译能力新增14个直译模型,打造以中文为轴心语言的翻译系统
经济全球化的今天,人们在工作和生活中经常会与外语打交道。相较传播性较广的英语而言,其他语种的识别和阅读对大多数人来说是一件难事,此时就需要借助语言翻译软件来帮助理解。 华为 HMS Core 机器学习服务(ML Kit)翻…...
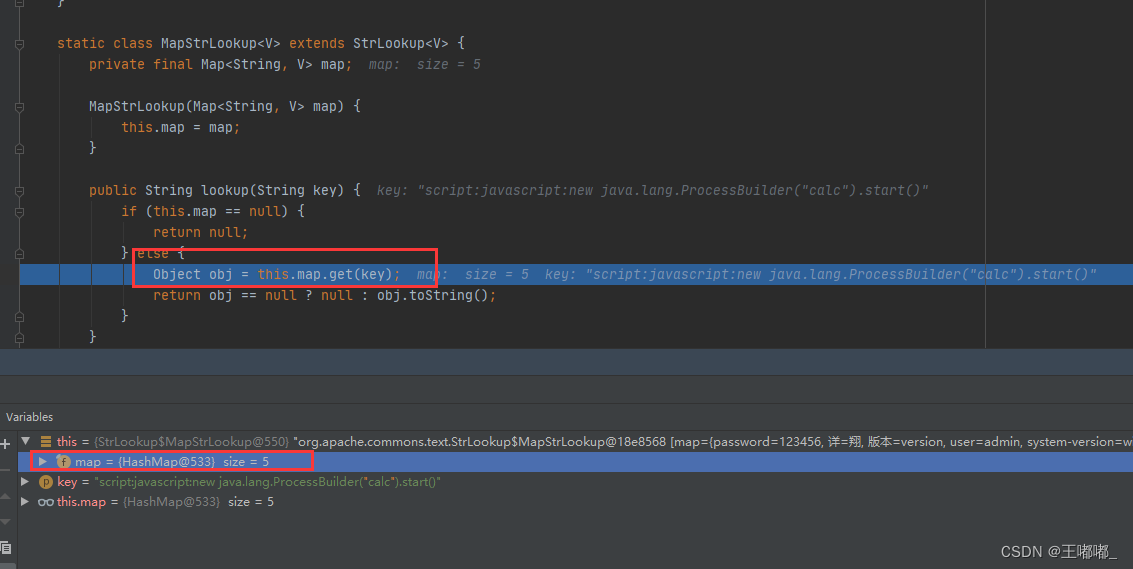
CVE-2022-42889 Apache Commons Text 漏洞
0x00 前言 所幸遇到,就简单看看,其中没有啥比较难的地方,仅做记录。10月13日的漏洞。 cve链接可以看下面这个: https://cve.mitre.org/cgi-bin/cvename.cgi?nameCVE-2022-42889 git地址: https://github.com/apache…...

20- widedeep及函数式构建模型 (TensorFlow系列) (深度学习)
知识要点 wide&deep: 模型构建中, 卷积后数据和原始数据结合进行输出.fetch_california_housing:加利福尼亚的房价数据,总计20640个样本,每个样本8个属性表示,以及房价作为target,所有属性值均为number࿰…...
大家一起做测试的,凭什么你现在拿20k,我却还只有10k?...
最近我发现一个神奇的事情,我一个97年的朋友居然已经当上了测试项目组长,据我所知他去年还是在深圳的一家创业公司做苦逼的测试狗,短短8个月,到底发生了什么? 于是我立刻私聊他八卦一番。 原来他所在的公司最近正在裁…...

>>数据管理:DAMA简介「考试和续期」
关于DAMA,这里就不再多做描述,可以参考以前写的一些简介或官方介绍。下面就考试再做一些详细介绍。 1 区别 CDGA:数据治理工程师(Certified Data Governance Associate),“DAMA中国”组织的数据治理方面的职业认证考试。 CDGP:数据治理专家(Certified Data Governa…...

React的生命周期详细讲解
什么是生命周期? 所谓的React生命周期,就是指组件从被创建出来,到被使用,最后被销毁的这么一个过程。而在这个过程中,React提供了我们会自动执行的不同的钩子函数,我们称之为生命周期函数。**组件的生命周期…...

蓝蓝算法二期工程day3,一万年太久,只争朝夕
思路: 最好想的是用hashmap,当然用c的话也可以用两个数组,一个数组用于存放字符串,自动对应ACSII码,一个将对应ACSII码的数字对应其下标,当然这也是用的映射的思想。 import java.util.*;public class Cac…...

程序代码的自动化生成方案设计
程序设计就能够适用这种代码自动化生成方法的前提是:PLC 程序代码具有高度重复性,执行的是相同数据处理或者逻辑判断,而相关变量组 是离 散 的,没 有规 律 可循 。以 I/O 变量和中间 变量的地 址 映 射 程序为例 ,程序代码为赋 值 语 句 ,高度重复;IO 变量和与 其 对应 的中间 …...

Go 稀疏数组学习与实现
仍然还是一个数组 基本介绍 一般就是指二维以上的数组 当一个数组中大部分元素是0 ,或者为同一个值的数组时,可以使用系数数组来保存该数组. 稀疏数组的处理方法: 记录数组一共有几行几列,有多少个不同的值把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
