Go 稀疏数组学习与实现
仍然还是一个数组
基本介绍
一般就是指二维以上的数组
当一个数组中大部分元素是0 ,或者为同一个值的数组时,可以使用系数数组来保存该数组.
稀疏数组的处理方法:
- 记录数组一共有几行几列,有多少个不同的值
- 把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模.
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SlBq9xxF-1677594413402)(…/…/images/Pasted%20image%2020230228201055.png)]
这就是一个六行七列的二维数组.
所以用一个n行三类的二维数组来记录这个数组
第一列是行数, 第二列是列数, 第三列是值
6 7 0
0 3 22
0 6 15
…
5 2 28
这里的6 7 0 记录的是这个二维数组有6 行7 列 的0 值
其余行记录不一样的值的位置
这是一种压缩
但是我们可以发现,一个数值会多出两个值(行列)来表示,所以如果有值的数,大于了原来数组的1/3 就得不偿失了
代码实现
一个二维数组转换成稀疏数组
package main //稀疏数组 type ValueNode struct { row int col int Val int
} func main() { // 创建一个原始的数组 var chessMap [11][11]int chessMap[1][2] = 1 chessMap[2][3] = 2 // 1 代表黑子 //2 代表白子 //输出原始数组 for _, item1 := range chessMap { for _, item2 := range item1 { print(item2) } println() } // 转换成稀疏数组 /* 思路 1.遍历数组,如果发现有一个元素的值不是0 ,就创建一个node结构体 2.将其放入到对应的切片中就可以了 */ var SparseArr []ValueNode //标准的稀疏数组要记录二维数组的行和列 valueNode := ValueNode{ row: 11, col: 11, Val: 0, } SparseArr = append(SparseArr, valueNode) // 结构体切片 //还是要全部扫描一遍的 for i, item1 := range chessMap { for j, item2 := range item1 { if item2 != 0 { // 创节点了 valueNode = ValueNode{ row: i, col: j, Val: item2, } SparseArr = append(SparseArr, valueNode) } } } // 输出稀疏数组 for i, valueNode := range SparseArr { println(i, valueNode.row, valueNode.col, valueNode.Val) } }将稀疏数组输入到一个文件中
package main import ( "bufio" "fmt" "os") //稀疏数组 type ValueNode struct { row int col int Val int
} func main() { path := "./resources/class.data" // 创建一个原始的数组 var chessMap [11][11]int chessMap[1][2] = 1 chessMap[2][3] = 2 // 1 代表黑子 //2 代表白子 //输出原始数组 for _, item1 := range chessMap { for _, item2 := range item1 { print(item2) } println() } //Arr2Sparse(chessMap) // 转换成稀疏数组 /* 思路 1.遍历数组,如果发现有一个元素的值不是0 ,就创建一个node结构体 2.将其放入到对应的切片中就可以了 */ var SparseArr []ValueNode //标准的稀疏数组要记录二维数组的行和列 valueNode := ValueNode{ row: 11, col: 11, Val: 0, } SparseArr = append(SparseArr, valueNode) // 结构体切片 //还是要全部扫描一遍的 for i, item1 := range chessMap { for j, item2 := range item1 { if item2 != 0 { // 创节点了 valueNode = ValueNode{ row: i, col: j, Val: item2, } SparseArr = append(SparseArr, valueNode) } } } //输出稀疏数组 file, err := os.OpenFile(path, os.O_WRONLY, 0666) if err != nil { fmt.Println("文件打开失败", err) } defer file.Close() for _, valueNode := range SparseArr { s := fmt.Sprintf("%d %d %d\n", valueNode.row, valueNode.col, valueNode.Val) write := bufio.NewWriter(file) write.WriteString(s) write.Flush() if err != nil { println("写入失败") } } }
稀疏数组变成二维数组
package main import ( "bufio" "fmt" "os") //稀疏数组 type ValueNode struct { row int col int Val int
} func main() { path := "./resources/class.data" // 恢复原始的数组 // 打开稀疏数组的文件 // 文件转换成稀疏数组(切片) var sparse []ValueNode file, _ := os.Open(path) defer file.Close() r := bufio.NewReader(file) for true { line, _, err := r.ReadLine() if err != nil { break } str := string(line) var ( num1 int num2 int num3 int ) fmt.Sscanf(str, "%d %d %d", &num1, &num2, &num3) //println(num1, num2, num3) valnode := ValueNode{ row: num1, col: num2, Val: num3, } sparse = append(sparse, valnode) } //fmt.Println(sparse) // 得到数据 //创建一个二维数组 chessMap := make([][]int, sparse[0].row) for i := 0; i < sparse[0].row; i++ { chessMap[i] = make([]int, sparse[0].col) } //fmt.Println(chessMap) // 遍历稀疏数组 for _, valNode := range sparse { //跳过第一个,不然会数组越界 if valNode.Val == 0 { continue } /* 或者 if index !=0 { chessMap[valNode.row][valNode.col] = valNode.Val } */ chessMap[valNode.row][valNode.col] = valNode.Val } // 输出恢复后的数据 for _, v := range chessMap { for _, v2 := range v { print(v2) } println() }
}
相关文章:

Go 稀疏数组学习与实现
仍然还是一个数组 基本介绍 一般就是指二维以上的数组 当一个数组中大部分元素是0 ,或者为同一个值的数组时,可以使用系数数组来保存该数组. 稀疏数组的处理方法: 记录数组一共有几行几列,有多少个不同的值把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程…...

MySQL 学习笔记(借鉴黑马程序员MySQL)
MySQL视频课链接 MySQL概述 数据库相关概念 数据库是存储数据的仓库,数据是有组织的进行存储(DataBase) 数据库管理系统是操纵和管理数据库的大型软件(DataBase Management System) SQL是操作关系型数据库的编程语…...

中级工程师职称申报到底需要参加答辩不?
获得中级工程师职称的方式有认定、评审、考试这几种形式。 甘建二老师先来简单说一下关于认定和考试这两种: 1.认定:中级职称认定一般是根据各地职称认定政策,如果你想走认定渠道,首先本人简历条件、业绩、奖项等非常优秀&#…...
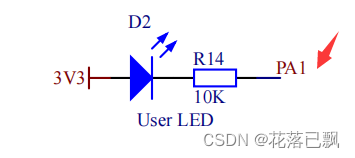
MM32开发教程(LED灯)
文章目录前言一、MM32介绍和STM32的区别二、板载LED灯原理图三、代码编写总结前言 今天将为大家介绍一款性能高体积小的MM32,这款开发板出自百问网团队。他就是灵动的MM32F3273,他体积非常小便于携带。 有128KB的SRAM、512KB的Flash、而且还支持双TypeC…...
win10安装docker
1.win10安装docker,前提必须是要安装WSL2。 现在Docker Desktop默认使用WSL 2来运行,而不是以前的Hyper-V。 WSL2 全称是Windows Subsystem on Linux。意思是,在win10,可以直接启动一个Linux。因为docker依赖Linux内核。 可查看…...
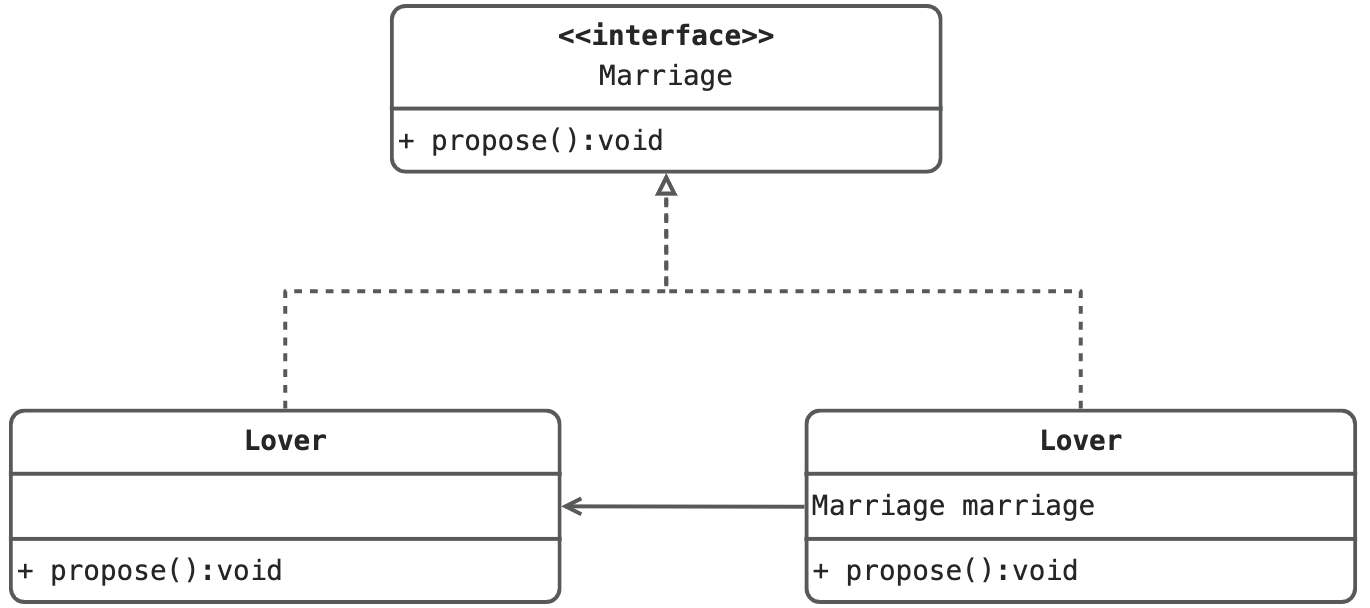
设计模式系列 - 代理模式及动态代理详解
定义 为其他对象提供一种代理以控制对这个对象的访问。在某些情况下,一个对象不适合或者不能直接引用另一个对象,而代理对象可以在客户端和目标对象之间起到中介的作用。 结构 抽象角色:通过接口或抽象类声明真实角色实现的业务方法。 代…...

【分享】订阅集简云畅捷通T+cloud连接器自动同步财务费用单至畅捷通
方案场景 伴随公司发展和数字化水平提高,大量的财务单据需要手动审核和录入,这些重复机械的操作占据大量人力,同时极容易出现数据出错或丢失等情况,严重影响着企业经营效率。 使用集简云提供服务的畅捷通TCloud钉钉连接器完成财…...

GPT的发展历程
GPT是当前最火的人工智能技术之一,自推出以来就广受关注。但大家对这个技术了解多少,又知道它经历了什么? GPT的诞生离不开谷歌在人工智能领域的努力和研究。2004年,谷歌成立了人工智能实验室(现已成为谷歌 AI实验室&…...

iOS开发笔记之九十八——关于Memory Leak总结笔记
*****阅读完此文,大概需要3分钟******关于Memory leak(内存泄漏)的问题,如果是面试被问这个问题以及此类问题,主要涉及下面3个方面:内存泄漏的常见场景有哪些,列举几个常见的例子?开…...
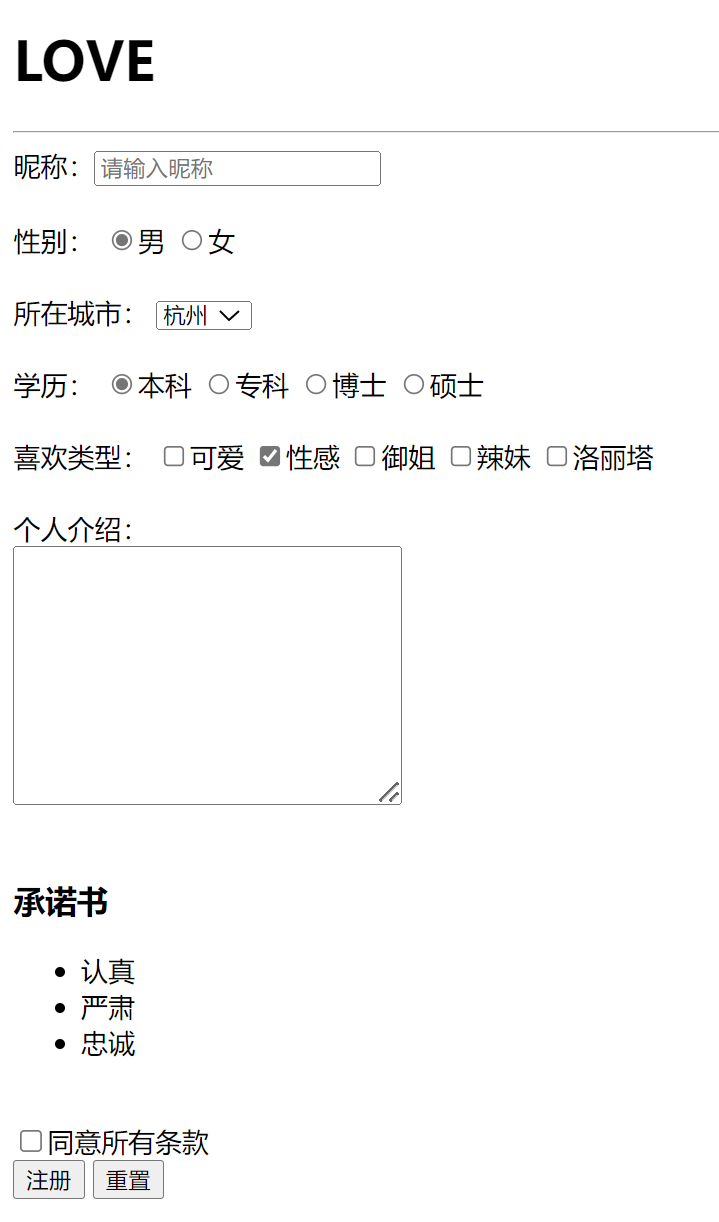
HTML基础语法
一 前端简介构成语言说明结构HTML页面元素和内容表现CSS网页元素的外观和位置等页面样式(美化)行为JavaScript网页模型的定义和页面交互二 HTML1.简介HTML(Hyper Text Markup Language):超文本标记语言。网页结构整体&…...

微软新版必应gpt人工智能体验教程
大家好,我是雄雄,欢迎关注微信公众号:** 雄雄的小课堂 ** 现在是:2023年2月28日18:35:02 前言 前几天,发了一篇文章,主要介绍了如何申请新必应的内测名单,其实一共也就那几步,然后等着就行: 文章连接:new bing如何快速申请内测资格,从而体验人工智能? 今天,终于…...

你问我答|虚拟机、容器和无服务器,怎么选?
在新技术层出不穷的当下,每家企业都希望不断降低成本,并提高运营效率,一个方法就是寻找不同的技术方案来优化运营。 例如,曾经一台服务器只能运行一个应用(裸机);接着,一台服务器的资源可以划分为多个块,从而运行多个应用(虚拟化);再到后来,应用越来越多,为了方便它们…...
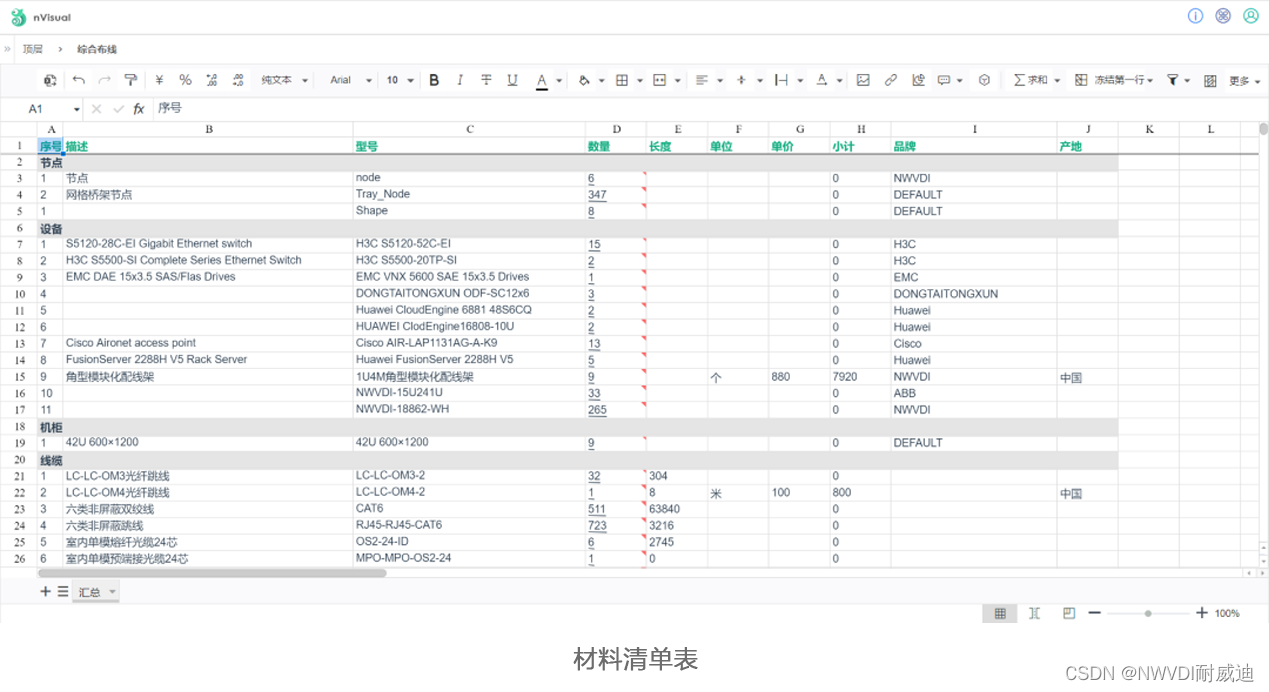
某建筑设计研究院“综合布线管理软件”应用实践
某建筑设计研究院有限公司(简称“某院”)隶属于国务院国资委直属的大型骨干科技型中央企业。“某院”前身为中央直属设计公司,创建于1952年。成立近70年来,始终秉承优良传统,致力于推进国内勘察设计产业的创新发展&…...
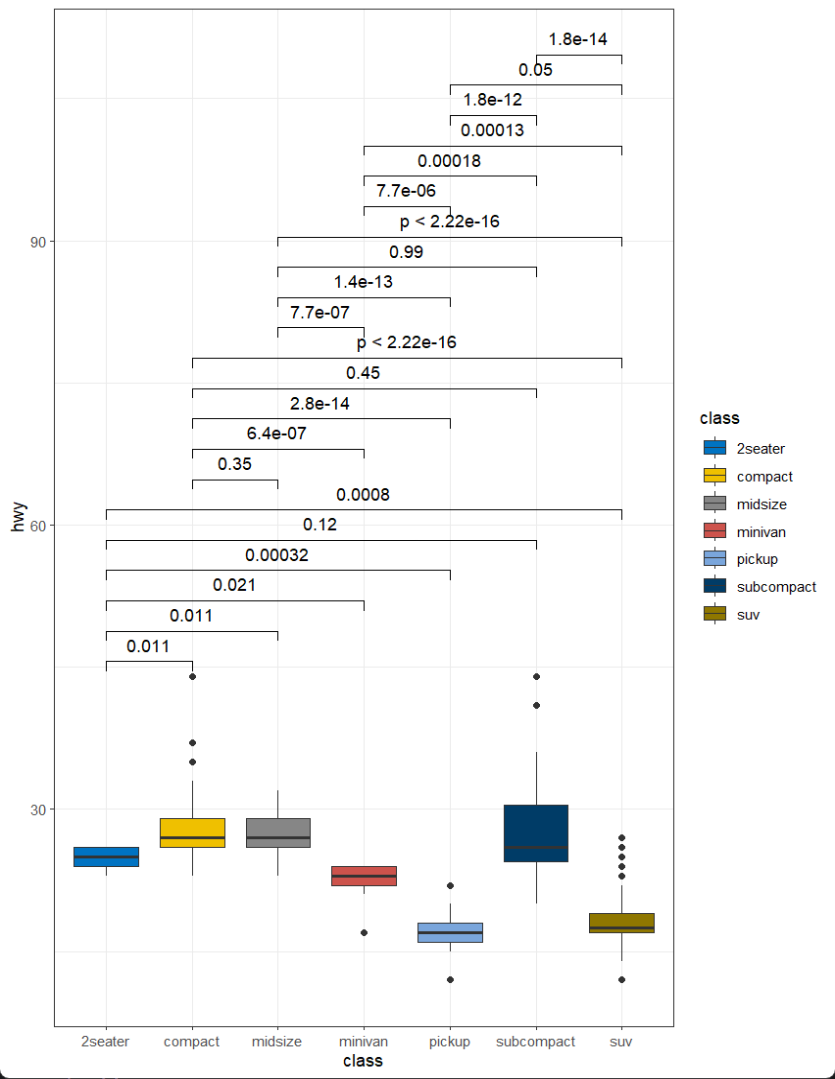
R语言绘制SCI论文中常见的箱线散点图,并自动进行方差分析计算显著性水平
显著性标记箱线散点图 本篇笔记的内容是在R语言中利用ggplot2,ggsignif,ggsci,ggpubr等包制作箱线散点图,并计算指定变量之间的显著性水平,对不同分组进行特异性标记,最终效果如下。 加载R包 library(ggplo…...

redux-saga
redux-saga 官网:About | Redux-Saga 中文网:自述 Redux-Saga redux-saga 是一个用于管理 异步获取数据(副作用) 的redux中间件;它的目标是让副作用管理更容易,执行更高效,测试更简单,处理故障时更容易… …...

【C++】-- 智能指针
目录 智能指针意义 智能指针的使用及原理 RAII 智能指针的原理 std::auto_ptr std::auto_ptr的模拟实现 std::unique_ptr std::unique_ptr模拟实现 std::shared_ptr std::shared_ptr的模拟实现 循环引用问题 智能指针意义 #问:为什么需要智能指针&#…...
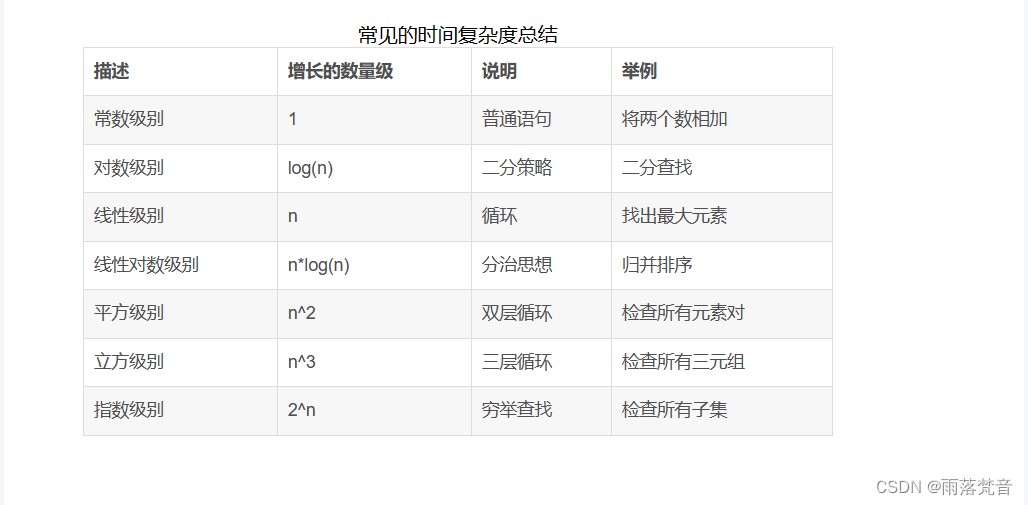
数据结构与算法——4时间复杂度分析2(常见的大O阶)
这篇文章是时间复杂度分析的第二篇。在前一篇文章中,我们从0推导出了为什么要用时间复杂度,时间复杂度如何分析以及时间复杂度的表示三部分内容。这篇文章,是对一些常用的时间复杂度进行一个总结,相当于是一个小结论 1.常见的大O…...

IIS解析漏洞
IIS 6.0在解析文件时存在以下两个解析漏洞。 ①当建立*.asa、*.asp格式的文件夹时,其目录下的任意文件都将被IIS当作asp文件来解析。 例如:建立文件夹 parsing.asp,在 parsing.asp 文件夹内新建一个文本文档 test.txt,其内容为&…...
)
2023 年腾讯云轻量和CVM服务器租用价格表出炉(CPU/内存/带宽/系统盘)
腾讯云服务器的价格表是用户比较关心的问题,服务器的价格组成包括云服务器的机型价格、磁盘价格和宽带价格,主机教程网来详细说下腾讯云最新的云服务器价格表。我们以北京一区、Linux系统的云服务器为例,其他地域的价格会有所差异,…...

Java学习之路002——面向对象编程
【说明】部分内容来源于网络,如有冲突,请联系作者删除。 一、面向对象编程(OOP) 2.1 对象和类的关系 2.2 面向对象的特征 2.2.1 封装 2.2.2 继承 2.2.3 多态 3、抽象 使用abstract关键字修饰的类或者方法 定义抽象类(使用abstract) // 1、定义抽象方法…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
