数据结构与算法——4时间复杂度分析2(常见的大O阶)
这篇文章是时间复杂度分析的第二篇。在前一篇文章中,我们从0推导出了为什么要用时间复杂度,时间复杂度如何分析以及时间复杂度的表示三部分内容。这篇文章,是对一些常用的时间复杂度进行一个总结,相当于是一个小结论
1.常见的大O阶
1.1线性阶
一般含有非嵌套循环(就是单层循环)涉及线性阶,线性阶就是随着输入规模的扩大,对应计算次数呈直线增长,例如下面的代码:
public static void main(String[] args) {int sum = 0;int n = 100;for (int i = 1; i <=n ; i++) {sum += i;}System.out.println("sum="+sum);}上面这段代码,它的循环的时间复杂度为O(n),因为循环体中的代码需要执行n次
1.2平方阶
一般嵌套循环(就是双层循环)属于这种时间复杂度
public static void main(String[] args) {int sum = 0;int n = 100;for (int i = 1; i <=n ; i++) {for (int j = 1; j <=n ; j++) {sum += i;}}System.out.println("sum="+sum);}上面这段代码,n=100,也就是说,外层循环每执行一次,内层循环就执行100次,那总共程序想要从这两个循环中出来,就需要执行100*100次,也就是n的平方次,所以这段代码的时间复杂度是O(n^2)
1.3立方阶
一般三层嵌套循环属于这种时间复杂度
public static void main(String[] args) {int x = 0;int n = 100;for (int i = 1; i <=n ; i++) {for (int j = 1; j <=n ; j++) {for (int k = 1; k <=n ; k++) {x ++; }}}System.out.println("x="+x);}上面这段代码,n=100,也就是说,外层循环每执行一次,中间循环循环就执行100次,中间循环每执行一次,最内层循环需要执行100次,那总共程序想要从这三个循环中出来,就需要执行100*100*100次,也就是n的立方,所以这段代码的时间复杂度是O(n^3)
1.4对数阶
对数,属于高中数学的内容,我们分析程序以程序为主,数学为辅,所以不用过分担心。
public static void main(String[] args) {int i = 0;int n = 100;while (i<n){i = i*2;}System.out.println("i="+i);}分析:
由于每次i*2之后,就距离n更近一步。我们假设有x个2相乘后大于n,那么x个2相乘后就会退出循环。那么就有公式:2^x=n,得到x=log(2)n。所以这个循环的时间复杂度为O(logn);
问:为什么底数可以忽略?
答:对于对数阶,由于随着输入规模n的增大,不管底数为多少,他们的增长趋势是一样的,所以我们会忽略底数。(其实就是找输入规模n与执行次数之间的抽象关系,抓取主要的,忽略次要的)
下面给出表和图,可以体会一下增长趋势:
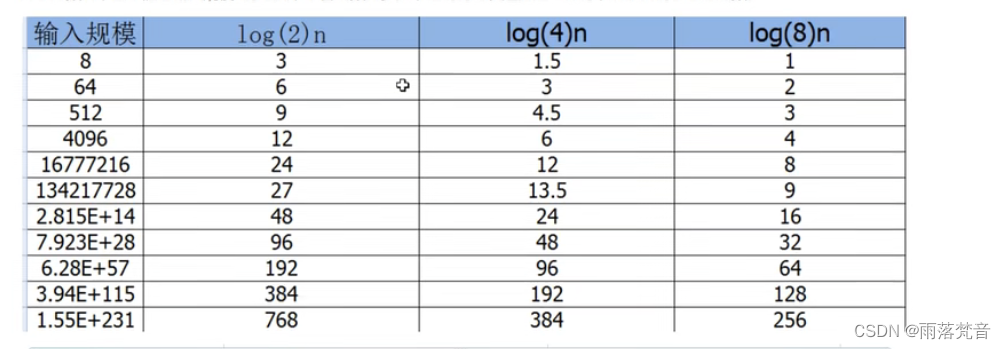
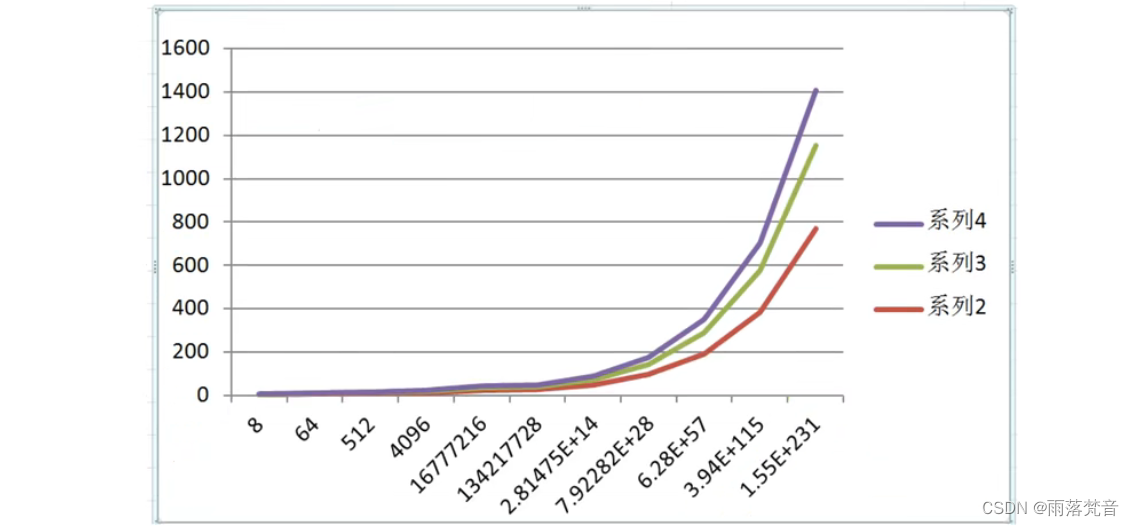
1.5常数阶
一般不涉及循环操作的都是常数阶,因为它不会随着n的增长而增加操作次数。例如︰
public static void main(String[] args) {int n = 100;int i = n+2;System.out.println("i="+i);}上述代码,不管输入规模n是多少,都执行2次,根据大O推导法则,常数用1来替换,所以上述代码的时间复杂度为O(1)
1.6小结
下面是对常见时间复杂度的一个总结:
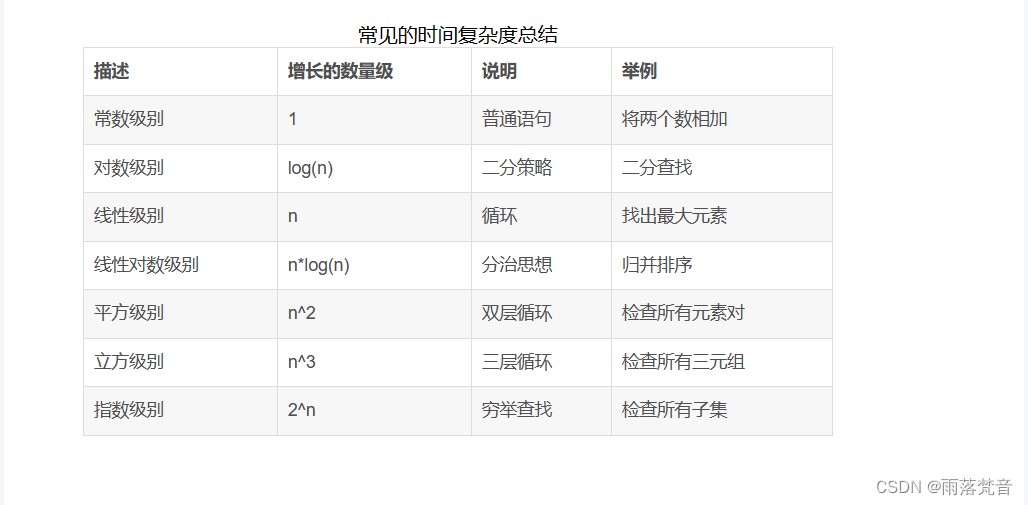
他们的时间复杂度从高到低依次是:
O(1)<O( log(n) )<O(n)<O(n*log(n))<O(n^2)<O(n^3)
根据前面的折线图分析,我们会发现,从平方阶开始,随着输入规模的增大,时间成本会急剧增大,所以,我们的算法,尽可能的追求的是O(1),O(log(n)),O(n),O(n^log(n))这几种时间复杂度,而如果发现算法的时间复杂度为平方阶、立方阶或者更复杂的,那我们可以分为这种算法是不可取的,需要优化。
2.函数调用的时间复杂度分析
之前,我们分析的都是单个函数内,算法代码的时间复杂度,接下来我们分析函数调用过程中时间复杂度。
2.1几个案例
案例一:
public static void main(String[] args) {int n = 100;for (int i = 0; i < n; i++) {show(i);}}public static void show(int i){System.out.println(i);}在main方法中,有一个for循环,循环体调用了show方法,由于show方法内部只执行了一行代码,所以show的时间复杂度为O(1),那main方法的时间复杂度就是O(n)
案例二:
public static void main(String[] args) {int n = 100;for (int i = 0; i < n; i++) {show(i);}}public static void show(int i){for (int j = 0; j < i; j++) {System.out.println(i);}}在main方法中,有一个for循环,循环体调用了show方法,由于show方法内部也有一个for循环,所以show方法的时间复杂度为O(n),那main方法的时间复杂度为O(n^2)
案例三:
public static void main(String[] args) {int n = 100;for (int i = 0; i < n; i++) {show(i);}for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {System.out.println(j);}}}public static void show(int i){for (int j = 0; j < i; j++) {System.out.println(i);}}在show方法中,有一个for循环,所以show方法的时间复杂度为o(n),在main方法中,show(n)这行代码内部执行的次数为n,第一个for循环内调用了show方法,所以其执行次数为n^2,第二个嵌套for循环内只执行了一行代码,所以其执行次数为n^2,那么main方法总执行次数为n+n^2+n^2=2n^2+n。
根据大O推导规则,去掉n保留最高阶项,并去掉最高阶项的常数因子2,所以最终main方法的时间复杂度为O(n^2)
2.2最坏情况
从心理学角度讲,每个人对发生的事情都会有一个预期,比如看到半杯水,有人会说︰哇哦,还有半杯水哦!但也有人会说∶天哪,只有半杯水了。一般人处于一种对未来失败的担忧,而在预期的时候趋向做最坏的打算,这样即使最糟糕的结果出现,当事人也有了心理准备,比较容易接受结果。假如最糟糕的结果并没有出现,当事人会很快乐。
算法分析也是类似,假如有一个需求∶
有一个存储了n个随机数字的数组,请从中查找出指定的数字。
public static void main(String[] args) {int a = search(5);System.out.println(a);}public static int search(int num){int[] arr = {11,5,3,6,7,15,6,9};for (int i = 0; i < arr.length; i++) {if (num == arr[i]) {return i;}}return -1;}最好情况:
查找的第一个数字就是期望的数字,那么算法的时间复杂度为O(1)
最坏情况:
查找的最后一个数字,才是期望的数字,那么算法的时间复杂度为O(n)
平均情况:
任何数字查找的平均成本是O(n/2)
最坏情况是一种保证,在应用中,这是一种最基本的保障,即使在最坏情况下,也能够正常提供服务,所以,除非特别指定,我们提到的运行时间都指的是最坏情况下的运行时间。
3.小结
这篇文章,我们总结了一些常见的大O阶,然后给出了相应的表格,这属于是一种结论,可以记下来的。然后我们分析了函数调用时的时间复杂度,其实和之前的分析方法是一样的。最后,我们讲了一下最坏情况的分析。
至此,算法的时间复杂度的讲解已经完毕了。如果有失误的地方,敬请各位指出,谢谢大家!
相关文章:

数据结构与算法——4时间复杂度分析2(常见的大O阶)
这篇文章是时间复杂度分析的第二篇。在前一篇文章中,我们从0推导出了为什么要用时间复杂度,时间复杂度如何分析以及时间复杂度的表示三部分内容。这篇文章,是对一些常用的时间复杂度进行一个总结,相当于是一个小结论 1.常见的大O…...

IIS解析漏洞
IIS 6.0在解析文件时存在以下两个解析漏洞。 ①当建立*.asa、*.asp格式的文件夹时,其目录下的任意文件都将被IIS当作asp文件来解析。 例如:建立文件夹 parsing.asp,在 parsing.asp 文件夹内新建一个文本文档 test.txt,其内容为&…...
)
2023 年腾讯云轻量和CVM服务器租用价格表出炉(CPU/内存/带宽/系统盘)
腾讯云服务器的价格表是用户比较关心的问题,服务器的价格组成包括云服务器的机型价格、磁盘价格和宽带价格,主机教程网来详细说下腾讯云最新的云服务器价格表。我们以北京一区、Linux系统的云服务器为例,其他地域的价格会有所差异,…...

Java学习之路002——面向对象编程
【说明】部分内容来源于网络,如有冲突,请联系作者删除。 一、面向对象编程(OOP) 2.1 对象和类的关系 2.2 面向对象的特征 2.2.1 封装 2.2.2 继承 2.2.3 多态 3、抽象 使用abstract关键字修饰的类或者方法 定义抽象类(使用abstract) // 1、定义抽象方法…...
VR直播丨颠覆性技术革命,新型直播已经到来
细数当下最火热的营销手段,首先浮现脑海的无疑是“直播”。前有罗永浩、李佳琦,后有刘畊宏和东方甄选,直播如日中天,俨然成了大众足不出户就能休闲娱乐的重要途径。 而随着虚拟现实在“十四五规划”中被列入“建设数字中国”数字…...

【微信小程序】-- WXSS 模板样式- rpx import (十三)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...
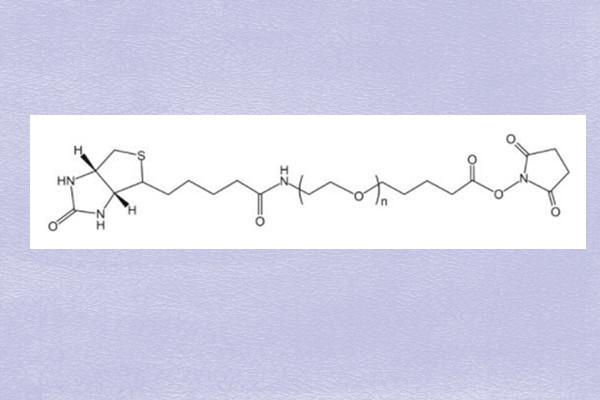
Biotin-PEG-SVA,生物素聚乙二醇琥珀酰亚胺戊酸酯,可用于检测或分子标记
Biotin-PEG-SVA 结构式:PEG分子量: 1000,2000,3400,5000,10000中文名称:生物素聚乙二醇琥珀酰亚胺戊酸酯,生物素-PEG-琥珀酰亚胺戊酸酯英文名称:Biotin-PEG-SVA …...
云原生是什么?核心概念和应用方法解析
什么是云原生? 云原生是一种基于容器、微服务和自动化运维的软件开发和部署方法。它可以使应用程序更加高效、可靠和可扩展,适用于各种不同的云平台。 如果要更直接通俗的来解释下上面的概念。云原生更准确来说就是一种文化,是一种潮流&…...
Editor工具开发实用篇:EditorGUI/EditorGUILayout的区别和EditorGUILayout的方法介绍
目录 一:EditorGUI和EditorGUILayout区别 二:EditorGUILayout 1.EditorGUILayout.BeginFadeGroup(float value); 2.EditorGUILayout.BeginHorizontal EditorGUILayout.BeginVertical 3.EditorGUILayout.BeginScrollView 4.EditorGUILayout.BeginT…...

(五十二)大白话不断在表中插入数据时,物理存储是如何进行页分裂的?.md
上回我们讲到了数据页的物理存储结构,数据页之间是组成双向链表的,数据页内部的数据行是组成单向链表的,每个数据页内根据主键做了一个页目录 然后一般来说,你没有索引的情况下,所有的数据查询,其实在物理…...

Unity 渲染顺序
Unity中的渲染顺序自上而下大致分为三层渲染优先级 Camera depth > Sorting Layer > Order in Layer > RenderQueueCamera depth:越小越优先(大的显示在小的前面)如图:尽管Sphere距离摄像机较远,但由于Camera_Sphere dep…...

短视频美颜sdk人脸编辑技术详解、美颜sdk代码分析
短视频美颜sdk中人脸编辑技术可以将人像风格进行转变,小编认为这也是未来的美颜sdk的一个重要发展方向,下文小编将为大家讲解一下短视频美颜sdk中人脸编辑的关键点。 一、人脸编辑的细分关键点 1、年龄 通过更改人脸的年龄属性,可用于模仿人…...

error: expected declaration specifiers or ‘...’ before ‘(’ token
一、问题 最近写函数时,遇到了一个比较奇怪的问题,相信也好多人遇到一下的问题: error: expected declaration specifiers or ‘...’ before ‘(’ token代码如下: #include<stdio.h> struct stu{char *name;int score;…...

系列七、索引
一、索引概述 1.1、概述 索引(index)是帮助MySQL高效获取数据的数据结构(有序)。在数据之外,数据库系统还维护着满足特定查找算法的数据结构,这些数据结构以某种方式引用(指向)数据, 这样就可以…...
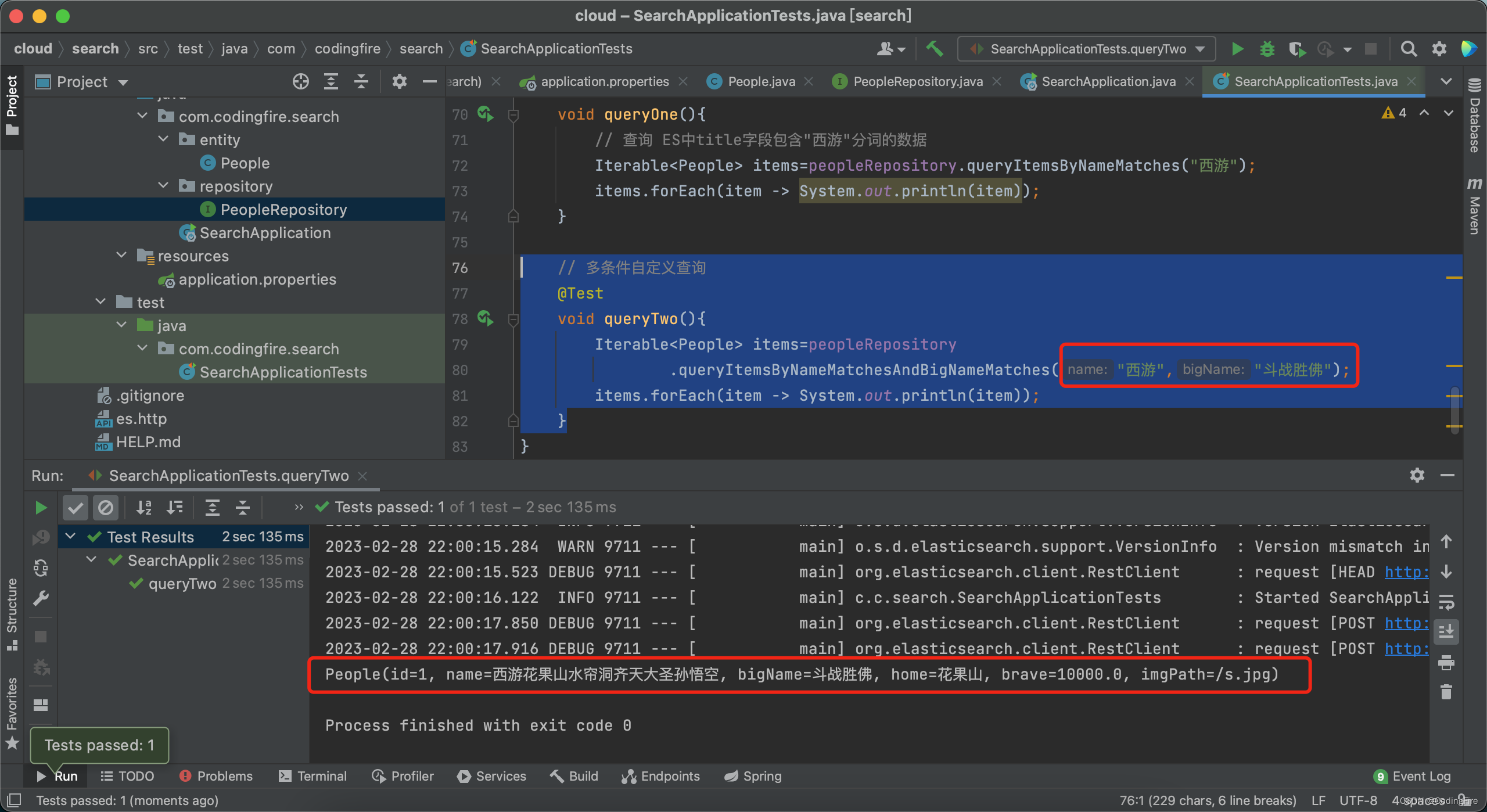
Java开发 - Elasticsearch初体验
目录 前言 什么是es? 为什么要使用es? es查询的原理? es需要准备什么? es基本用法 创建工程 添加依赖 创建操作es的文件 使用ik分词插件 Spring Data 项目中引入Spring Data 添加依赖 添加配置 创建操作es的业务逻…...
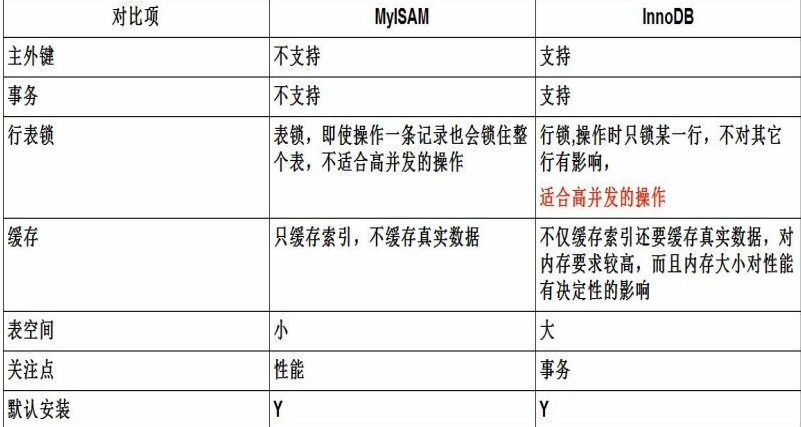
mysql进阶
mysql进阶视图视图是一个基于查询的虚拟表,封装了一条sql语句,通俗的解释,视图就是一条select查询之后的结果集,视图并不存储数据,数据仍旧存储在表中。创建视图语句:create view view_admin as select * from admin使…...
SD卡损坏了?储存卡恢复数据就靠这3个方法
作为一种方便的储存设备,SD卡在我们的日常生活中使用非常广泛。但是,有时候我们可能会遇到SD卡损坏的情况,这时候里面存储的数据就会受到影响。SD卡里面保存着我们很多重要的数据,有些还是工作必须要使用的。 如果您遇到了这种情…...
)
springboot+实践(总结到位)
一。【SpringBoot注解-1】 牛逼:云深i不知处 【SpringBoot注解-1】:常见注解总览_云深i不知处的博客-CSDN博客 二。【SpringBoot-3】Lombok使用详解 【SpringBoot-3】Lombok使用详解_云深i不知处的博客-CSDN博客_springboot lombok 三࿰…...
CorelDRAW2023新功能有哪些?最新版cdr下载安装教程
使用 CorelDRAW2023,随时随都能进行设计创作。在 Windows或Mac上使用专为此平台设计的直观界面,以自己的风格尽情自由创作。同全球数百万信赖CorelDRAW Graphics Suite 的艺术家、设计者及小型企业主一样,大胆展现真我,创作出众的…...

PLC 程序设计标准化方法
PLC 程序设计的标准化方法先从内容或者方法层面进行流程的分解,将分解的内容称为要素,要素的有机结合便构成了标准化的设计。流程标准化设计完成之后需要对各个要素分别进行标准化的设计。2.1、 PLC 程序设计的要素分解与有机结合根据软件程序设计的一般性方法结合PLC 程序设计…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
