【视觉SLAM十四讲学习笔记】第三讲——Eigen库
专栏系列文章如下:
【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍
【视觉SLAM十四讲学习笔记】第二讲——初识SLAM
【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动?
Eigen
Eigen是一个C++开源线性代数库。它提供了快速的有关矩阵的线性代数运算,还包括解方程等功能。
请输入以下命令进行安装:
sudo apt-get install libeigen3-dev
与其他库相比,Eigen的特殊之处在于,它是一个纯用头文件搭建起来的库,这意味着你只能找到它的头文件,而没有类似.so或者.a的二进制文件。在使用时,只需引入Eigen的头文件即可,不需要链接库文件(因为它没有库文件)。接下来对这个库的使用做一些示例:
#include <iostream>using namespace std;#include <ctime>
// Eigen 核心部分
#include <Eigen/Core>
// 稠密矩阵的代数运算(逆,特征值等)
#include <Eigen/Dense>using namespace Eigen;int main(int argc, char **argv) {// Eigen 中所有向量和矩阵都是Eigen::Matrix,它是一个模板类。它的前三个参数为:数据类型,行,列// 声明一个2*3的float矩阵Matrix<float, 2, 3> matrix_23;// 同时,Eigen 通过 typedef 提供了许多内置类型,不过底层仍是Eigen::Matrix// 例如 Vector3d 实质上是 Eigen::Matrix<double, 3, 1>,即三维向量Vector3d v_3d;// 这是一样的Matrix<float, 3, 1> vd_3d;// Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>Matrix3d matrix_33 = Matrix3d::Zero(); //初始化为零// 如果不确定矩阵大小,可以使用动态大小的矩阵Matrix<double, Dynamic, Dynamic> matrix_dynamic;// 更简单的MatrixXd matrix_x;// 这种类型还有很多,我们不一一列举// 下面是对Eigen阵的操作// 输入数据(初始化)matrix_23 << 1, 2, 3, 4, 5, 6;// 输出cout << "matrix 2x3 from 1 to 6: \n" << matrix_23 << endl;// 用()访问矩阵中的元素cout << "print matrix 2x3: " << endl;for (int i = 0; i < 2; i++) {for (int j = 0; j < 3; j++) cout << matrix_23(i, j) << "\t";cout << endl;}return 0;
}
输出结果:
matrix 2x3 from 1 to 6:
1 2 3
4 5 6
print matrix 2x3:
1 2 3
4 5 6
矩阵运算:
#include <iostream>using namespace std;#include <ctime>
#include <Eigen/Core>
#include <Eigen/Dense>using namespace Eigen;int main(int argc, char **argv) {// Eigen 中所有向量和矩阵都是Eigen::Matrix,它是一个模板类。它的前三个参数为:数据类型,行,列// 声明一个2*3的float矩阵Matrix<float, 2, 3> matrix_23;Vector3d v_3d;Matrix<float, 3, 1> vd_3d;// Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>Matrix3d matrix_33 = Matrix3d::Zero(); //初始化为零// 下面是对Eigen阵的操作// 输入数据(初始化)matrix_23 << 1, 2, 3, 4, 5, 6;// 矩阵和向量相乘(实际上仍是矩阵和矩阵)v_3d << 3, 2, 1;vd_3d << 4, 5, 6;// 但是在Eigen里你不能混合两种不同类型的矩阵,像这样是错的// Matrix<double, 2, 1> result_wrong_type = matrix_23 * v_3d;// 应该显式转换Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;cout << "[1,2,3;4,5,6]*[3,2,1]=" << result.transpose() << endl;Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;cout << "[1,2,3;4,5,6]*[4,5,6]: " << result2.transpose() << endl;// 一些矩阵运算// 四则运算就不演示了,直接用+-*/即可。matrix_33 = Matrix3d::Random(); // 随机数矩阵cout << "random matrix: \n" << matrix_33 << endl;cout << "transpose: \n" << matrix_33.transpose() << endl; // 转置cout << "sum: " << matrix_33.sum() << endl; // 各元素和cout << "trace: " << matrix_33.trace() << endl; // 迹cout << "times 10: \n" << 10 * matrix_33 << endl; // 数乘cout << "inverse: \n" << matrix_33.inverse() << endl; // 逆cout << "det: " << matrix_33.determinant() << endl; // 行列式// 特征值// 实对称矩阵可以保证对角化成功SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33);cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;return 0;
}
输出结果:
[1,2,3;4,5,6]*[3,2,1]=10 28
[1,2,3;4,5,6]*[4,5,6]: 32 77
random matrix: 0.680375 0.59688 -0.329554
-0.211234 0.823295 0.5364590.566198 -0.604897 -0.444451
transpose: 0.680375 -0.211234 0.5661980.59688 0.823295 -0.604897
-0.329554 0.536459 -0.444451
sum: 1.61307
trace: 1.05922
times 10: 6.80375 5.9688 -3.29554
-2.11234 8.23295 5.364595.66198 -6.04897 -4.44451
inverse:
-0.198521 2.22739 2.83571.00605 -0.555135 -1.41603-1.62213 3.59308 3.28973
det: 0.208598
Eigen values =
0.02428990.9921541.80558
Eigen vectors =
-0.549013 -0.735943 0.3961980.253452 -0.598296 -0.760134
-0.796459 0.316906 -0.514998
解方程:
#include <iostream>
#include <ctime>
#include <Eigen/Core>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;#define MATRIX_SIZE 50int main(int argc, char **argv) {// 解方程// 我们求解 matrix_NN * x = v_Nd 这个方程// N的大小在前边的宏里定义,它由随机数生成// 直接求逆自然是最直接的,但是求逆运算量大Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN= MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);matrix_NN = matrix_NN * matrix_NN.transpose(); // 保证半正定Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);clock_t time_stt = clock(); // 计时// 直接求逆Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;cout << "time of normal inverse is "<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;cout << "x = " << x.transpose() << endl;// 通常用矩阵分解来求,例如QR分解,速度会快很多time_stt = clock();x = matrix_NN.colPivHouseholderQr().solve(v_Nd);cout << "time of Qr decomposition is "<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;cout << "x = " << x.transpose() << endl;// 对于正定矩阵,还可以用cholesky分解来解方程time_stt = clock();x = matrix_NN.ldlt().solve(v_Nd);cout << "time of ldlt decomposition is "<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;cout << "x = " << x.transpose() << endl;return 0;
}
结果如下:
time of normal inverse is 2.606ms
x = -55.7896 -298.793 130.113 -388.455 -159.312 160.654 -40.0416 -193.561 155.844 181.144 185.125 -62.7786 19.8333 -30.8772 -200.746 55.8385 -206.604 26.3559 -14.6789 122.719 -221.449 26.233 -318.95 -78.6931 50.1446 87.1986 -194.922 132.319 -171.78 -4.19736 11.876 -171.779 48.3047 84.1812 -104.958 -47.2103 -57.4502 -48.9477 -19.4237 28.9419 111.421 92.1237 -288.248 -23.3478 -275.22 -292.062 -92.698 5.96847 -93.6244 109.734
time of Qr decomposition is 3.419ms
x = -55.7896 -298.793 130.113 -388.455 -159.312 160.654 -40.0416 -193.561 155.844 181.144 185.125 -62.7786 19.8333 -30.8772 -200.746 55.8385 -206.604 26.3559 -14.6789 122.719 -221.449 26.233 -318.95 -78.6931 50.1446 87.1986 -194.922 132.319 -171.78 -4.19736 11.876 -171.779 48.3047 84.1812 -104.958 -47.2103 -57.4502 -48.9477 -19.4237 28.9419 111.421 92.1237 -288.248 -23.3478 -275.22 -292.062 -92.698 5.96847 -93.6244 109.734
time of ldlt decomposition is 1.38ms
x = -55.7896 -298.793 130.113 -388.455 -159.312 160.654 -40.0416 -193.561 155.844 181.144 185.125 -62.7786 19.8333 -30.8772 -200.746 55.8385 -206.604 26.3559 -14.6789 122.719 -221.449 26.233 -318.95 -78.6931 50.1446 87.1986 -194.922 132.319 -171.78 -4.19736 11.876 -171.779 48.3047 84.1812 -104.958 -47.2103 -57.4502 -48.9477 -19.4237 28.9419 111.421 92.1237 -288.248 -23.3478 -275.22 -292.062 -92.698 5.96847 -93.6244 109.734
这个例程演示了Eigen矩阵的基本操作与运算。要编译它,需要在CMakeLists.txt里指定Eigen的头文件目录:
#添加头文件
include_directories("/usr/include/eigen3")
因为Eigen库只有头文件,所以不需要再用target_link_libraries语句将程序链接到库上。
相关文章:

【视觉SLAM十四讲学习笔记】第三讲——Eigen库
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵 本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动? Eigen…...
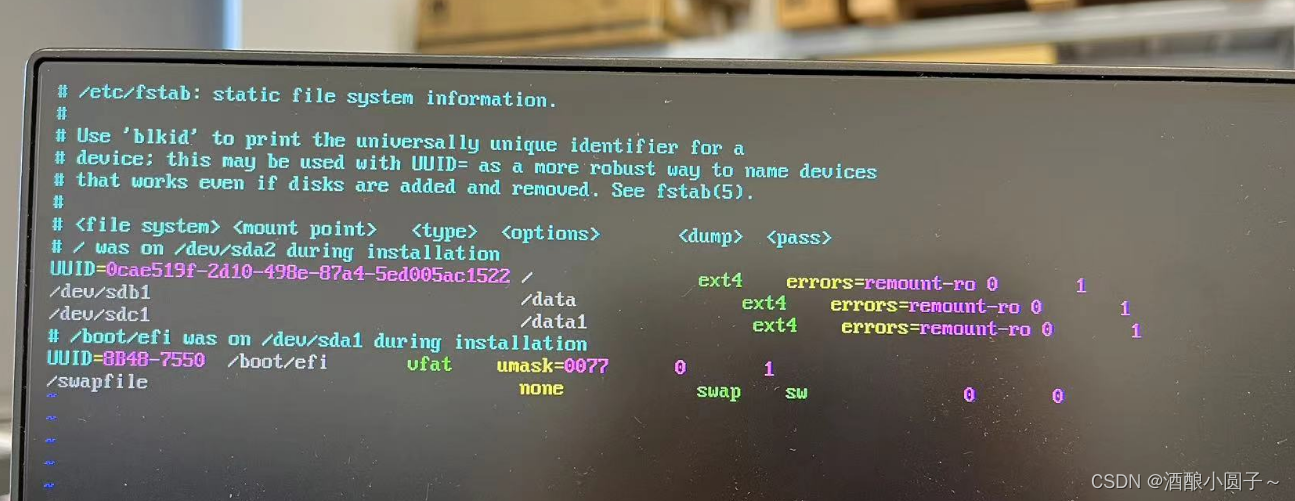
Ubuntu开机显示recovering journal,进入emergency mode
在一次正常的shutdown -r now之后,服务器启动不起来了,登录界面显示recovering journal,主要报错信息如下所示: /dev/sda2:recovering journal /dev/sda2:Clearn... You are in emergency mode. After logging in, type journalc…...

C++_String增删查改模拟实现
C_String增删查改模拟实现 前言一、string默认构造、析构函数、拷贝构造、赋值重载1.1 默认构造1.2 析构函数1.3 拷贝构造1.4 赋值重载 二、迭代器和范围for三、元素相关:operator[ ]四、容量相关:size、resize、capacity、reserve4.1 size、capacity4.2…...
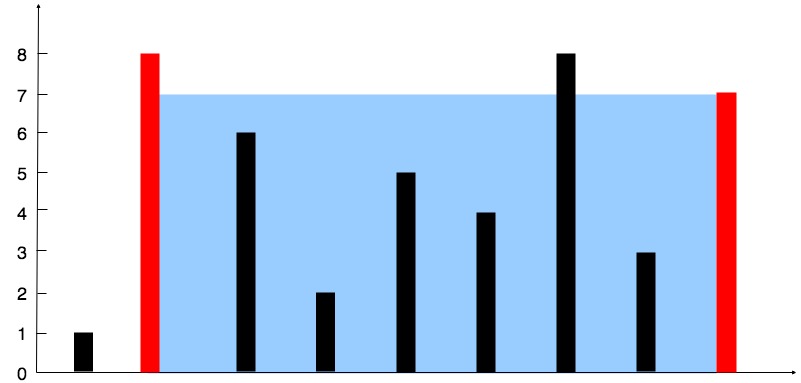
LeeCode前端算法基础100题(2)- 最多水的容器
一、问题详情: 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:…...

排序算法--归并排序
实现逻辑 ① 将序列每相邻两个数字进行归并操作,形成floor(n/2)个序列,排序后每个序列包含两个元素 ② 将上述序列再次归并,形成floor(n/4)个序列,每个序列包含四个元素 ③ 重复步骤②,直到所有元素排序完毕 void pri…...

【LeetCode:1410. HTML 实体解析器 | 模拟+哈希表+字符串+库函数】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
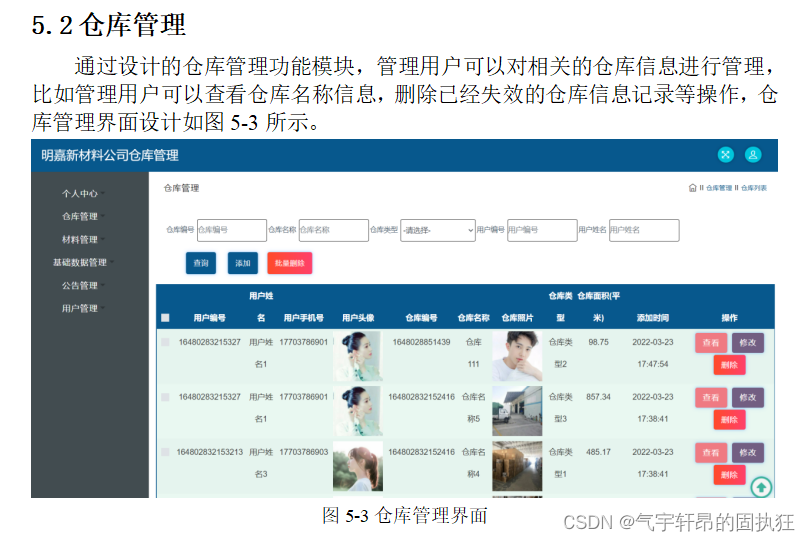
基于SSM的公司仓库管理系统(有报告)。Javaee项目
演示视频: 基于SSM的公司仓库管理系统(有报告)。Javaee项目 项目介绍: 采用M(model)V(view)C(controller)三层体系结构,通过Spring SpringMvc …...
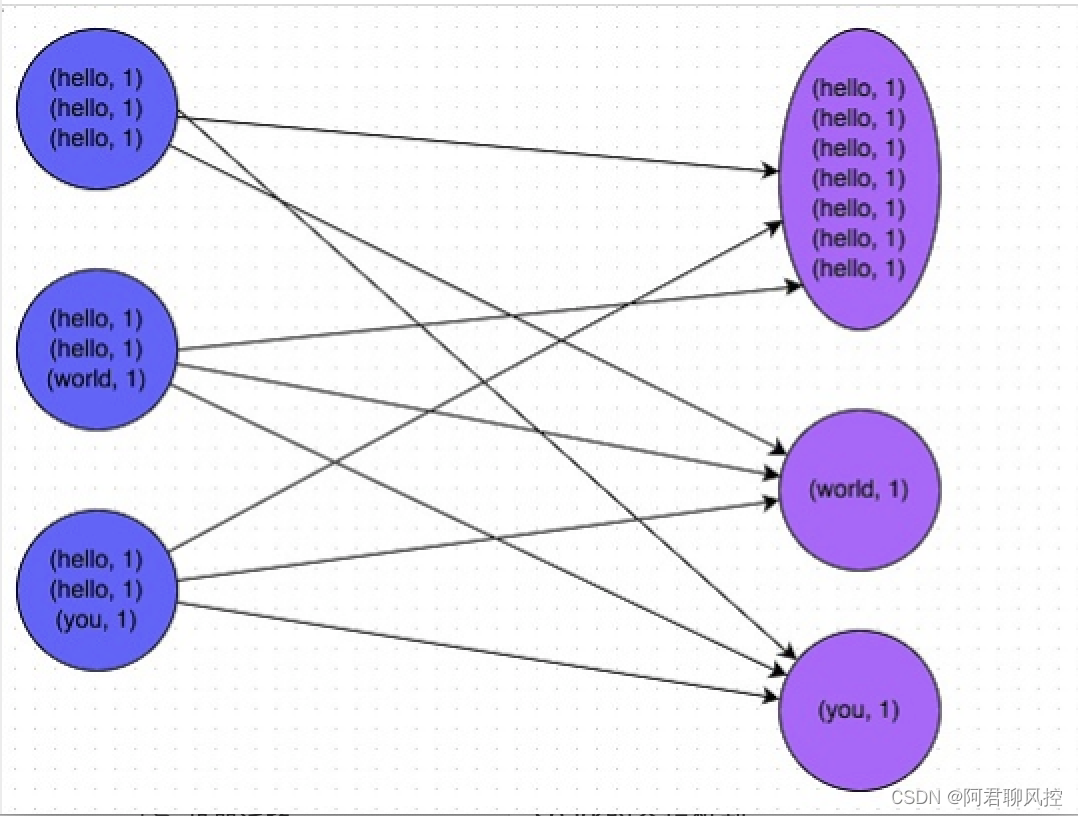
spark数据倾斜的解决思路
数据倾斜是:多个分区中,某个分区的数据比其他分区的数据多的多 数据倾斜导致的问题: 导致某个spark任务耗时较长,导致整个任务耗时增加,甚至出现OOM运行速度慢:主要发生在shuffle阶段,同样的k…...
Python武器库开发-前端篇之html概述(二十八)
前端篇之html概述(二十八) html概述 HTML5是构建Web内容的一种语言描述方式。HTML5是互联网的下一代标准,是构建以及呈现互联网内容的一种语言方式.被认为是互联网的核心技术之一。HTML产生于1990年,1997年HTML4成为互联网标准,…...
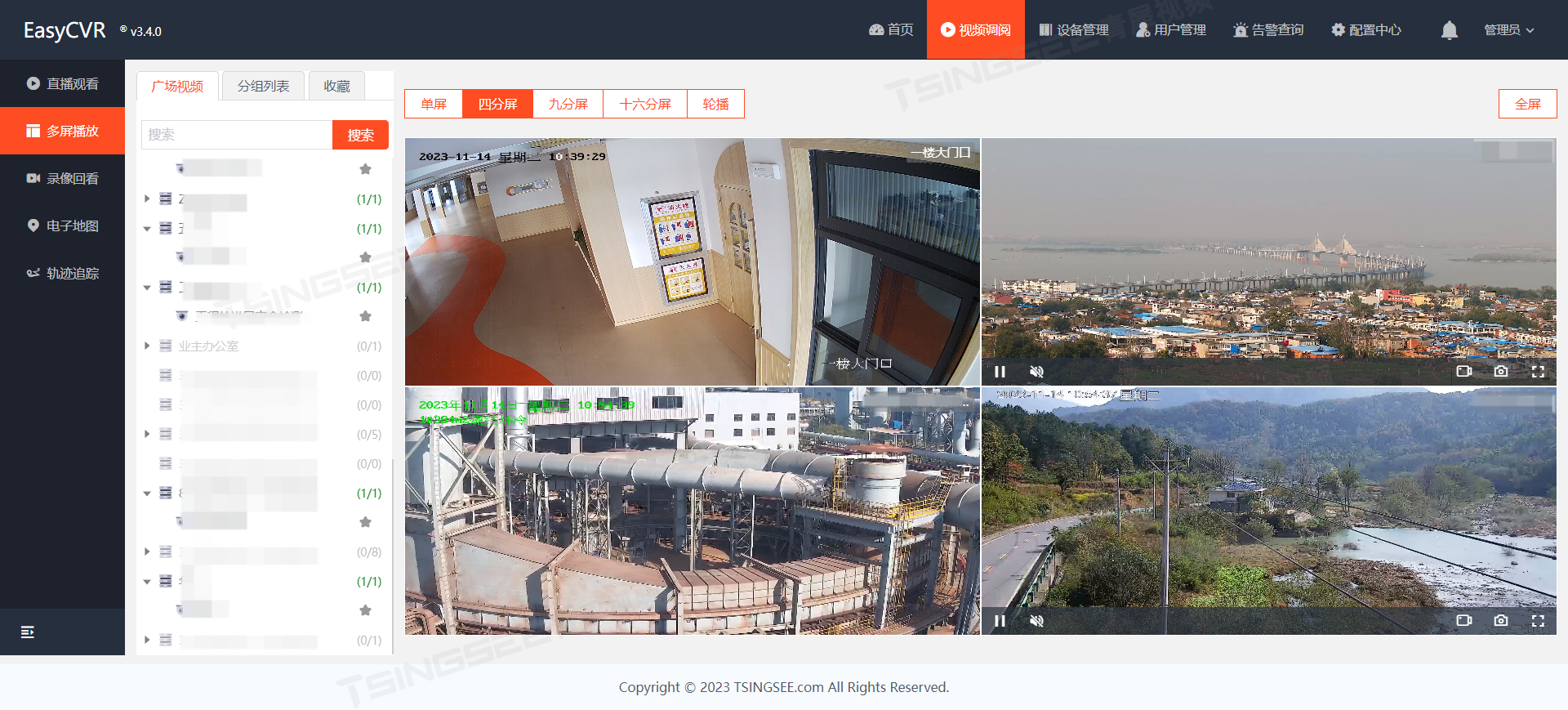
安防视频EasyCVR平台太阳能供电+4G摄像头视频监控方案的建设
在工地、光伏、风电站、水库河道等场景中,以及一些偏远地区的项目现场,会存在无网无电情况,大大制约了视频监控系统建设的效率及可行性。在这种场景中,我们也可以通过太阳能供电4G监控摄像机的方案,满足偏远地区无网无…...
)
12.位运算的性质(异或的性质)
文章目录 异或的性质求异或和问题[421. 数组中两个数的最大异或值](https://leetcode.cn/problems/maximum-xor-of-two-numbers-in-an-array/)[2935. 找出强数对的最大异或值 II](https://leetcode.cn/problems/maximum-strong-pair-xor-ii/) 异或前缀和问题(最..回…...
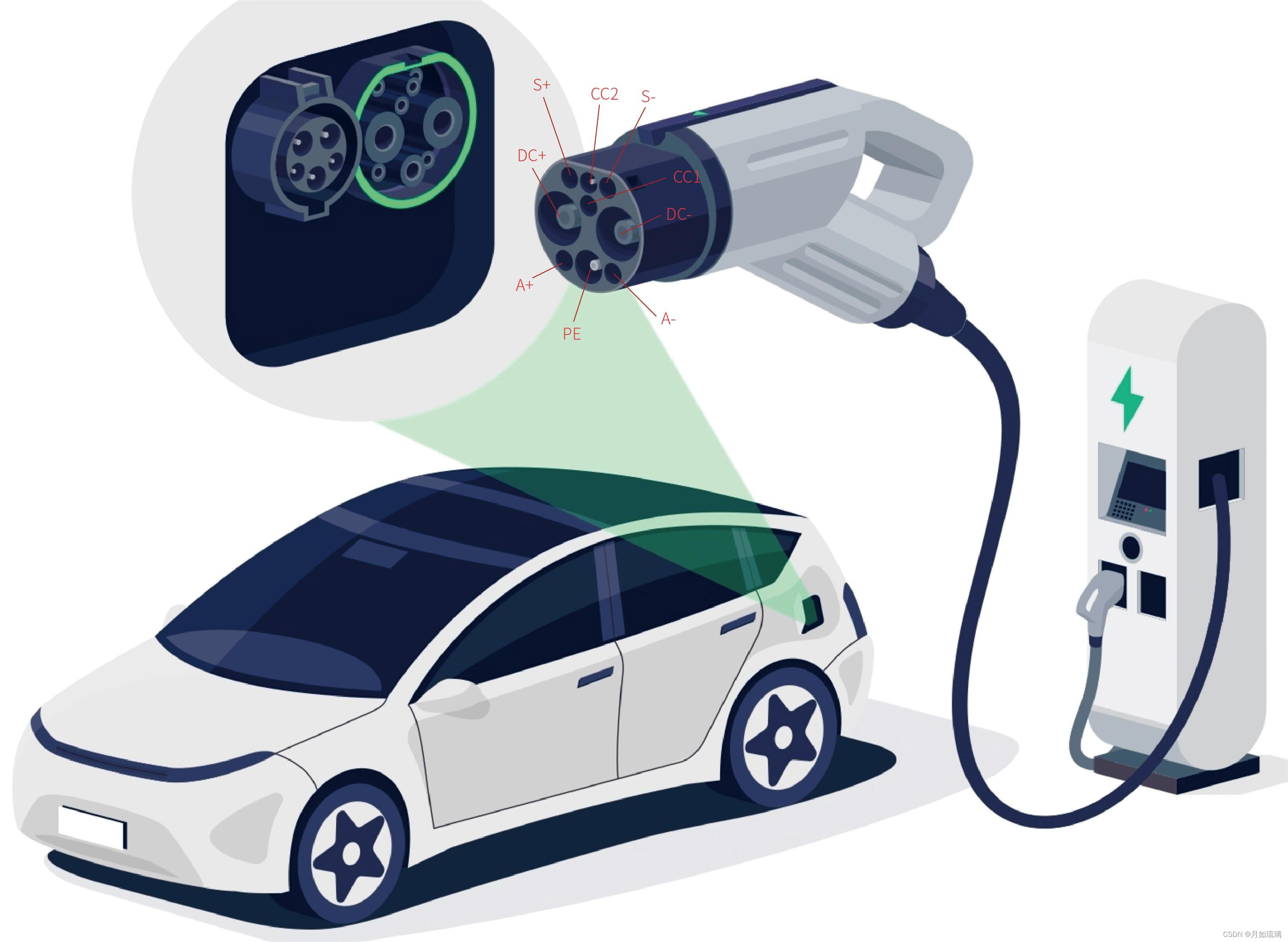
国标直流充电枪9孔分别啥意思?
DC:直流电源正 DC-:直流电源负 PE:接地(搭铁)S:通讯CAN-H S-:通讯CAN-L CC1:充电连接确认 CC2:充电连接确认 A:12V A-:12V- 以上就是国标直流充电…...

关于 Google AMP 和 SEO
Google 于 2015 年首次推出 AMP,即加速移动页面。借助开源 AMP 框架,网页设计师可以制作快速加载的移动网页。该框架的创建是为了应对使用移动设备访问互联网的个人数量的增加。从那时起,谷歌一直在推动使用 AMP 来增强移动设备上的 SEO 和用…...
【SpringMVC】 对请求的不同响应
前言 本文学习如何运用不同的注解来返回不同的响应. 1.返回静态页面Controller 返回index.html页面 Controller 和 RestController的区别 controller 只有加上这个注解,Spring才会帮我们管理这个代码.后续我们访问时才能访问到. RestController 等同于 Controller ResponseBo…...

SQL进阶学习
1.[NISACTF 2022]join-us sql报错注入和联合注入 过滤: as IF rand() LEFT by updatesubstring handler union floor benchmark COLUMN UPDATE & sys.schema_auto_increment_columns && 11 database case AND right CAST FLOOR left updatexml DATABA…...

邦芒解析:做好职场规划防止跳槽失败
为了防止跳槽进入不适合自己的工作环境,你可以采取以下措施: 1、做好调研:在决定跳槽之前,尽可能了解新公司的情况。这包括公司的文化、工作氛围、发展前景以及团队成员之间的关系等。通过搜索公司网站、阅读员工评价以及与公司内…...

基于springboot实现实习管理系统的设计与实现项目【项目源码+论文说明】计算机毕业设计
基于sprinmgboot实现实习管理系统的设计与实现演示 摘要 随着信息化时代的到来,管理系统都趋向于智能化、系统化,实习管理也不例外,但目前国内仍都使用人工管理,市场规模越来越大,同时信息量也越来越庞大,…...

【华为OD题库-031】比赛的冠亚季军-java
题目 有N(3<N<10000)个运动员,他们的id为0到N-1,他们的实力由一组整数表示。他们之间进行比赛,需要决出冠亚军。比赛的规则是0号和1号比赛,2号和3号比赛,以此类推,每一轮,相邻的运动员进行比赛&#…...
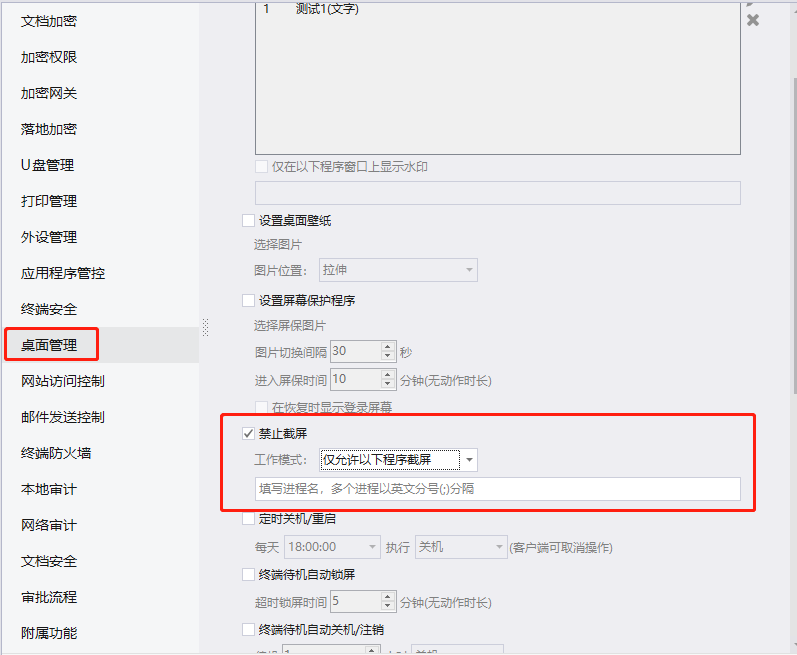
电脑如何禁止截屏
禁止电脑截屏是一项重要的安全措施,可以保护用户隐私和防止恶意软件的使用。以下是几种禁止电脑截屏的方法: 形式一: 一刀切,全部禁止截屏 可以在域之盾软件后,点击桌面管理,然后选择禁止截屏。就能禁止所…...
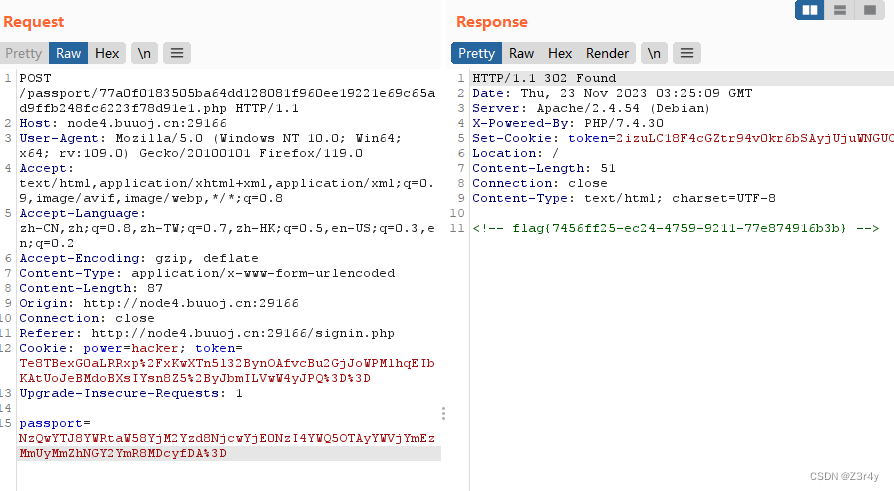
【Web】NewStarCTF Week1 个人复现
目录 ①泄露的秘密 ②Begin of Upload ③Begin of HTTP ④ErrorFlask ⑤Begin of PHP ⑥R!C!E! ⑦EasyLogin ①泄露的秘密 盲猜/robots.txt,访问得到flag前半部分 第二个没试出来,老老实实拿dirsearch扫吧 访问/www.zip 下载附件,拿到第二部分…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...
