【数据结构】树与二叉树(廿二):树和森林的遍历——后根遍历(递归算法PostOrder、非递归算法NPO)
文章目录
- 5.1 树的基本概念
- 5.1.1 树的定义
- 5.1.2 森林的定义
- 5.1.3 树的术语
- 5.2 二叉树
- 5.3 树
- 5.3.1 树的存储结构
- 1. 理论基础
- 2. 典型实例
- 3. Father链接结构
- 4. 儿子链表链接结构
- 5. 左儿子右兄弟链接结构
- 5.3.2 获取结点的算法
- 5.3.3 树和森林的遍历
- 1. 先根遍历(递归、非递归)
- 2. 后根遍历(递归)
- a.理论
- b. ADL算法PostOrder
- c. 代码实现
- 3. 后根遍历(非递归)
- a. ADL算法NPO
- b. NPO算法解析
- c. 代码实现
- 3. 森林的遍历
- 4. 代码整合
5.1 树的基本概念
5.1.1 树的定义
- 一棵树是结点的有限集合T:
- 若T非空,则:
- 有一个特别标出的结点,称作该树的根,记为root(T);
- 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0),其中T1, T2, …, Tm又都是树,称作root(T)的子树。
- T 空时为空树,记作root(T)=NULL。
- 若T非空,则:
5.1.2 森林的定义
一个森林是0棵或多棵不相交(非空)树的集合,通常是一个有序的集合。换句话说,森林由多个树组成,这些树之间没有交集,且可以按照一定的次序排列。在森林中,每棵树都是独立的,具有根节点和子树,树与树之间没有直接的连接关系。
森林是树的扩展概念,它是由多个树组成的集合。在计算机科学中,森林也被广泛应用于数据结构和算法设计中,特别是在图论和网络分析等领域。
5.1.3 树的术语
- 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(ancestor)
- 度(degree)、叶子节点(leaf node)、分支节点(internal node)
- 结点的层数
- 路径、路径长度、结点的深度、树的深度
参照前文:【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
5.2 二叉树
5.3 树
5.3.1 树的存储结构
1. 理论基础
2. 典型实例
3. Father链接结构
4. 儿子链表链接结构
【数据结构】树与二叉树(十八):树的存储结构——Father链接结构、儿子链表链接结构
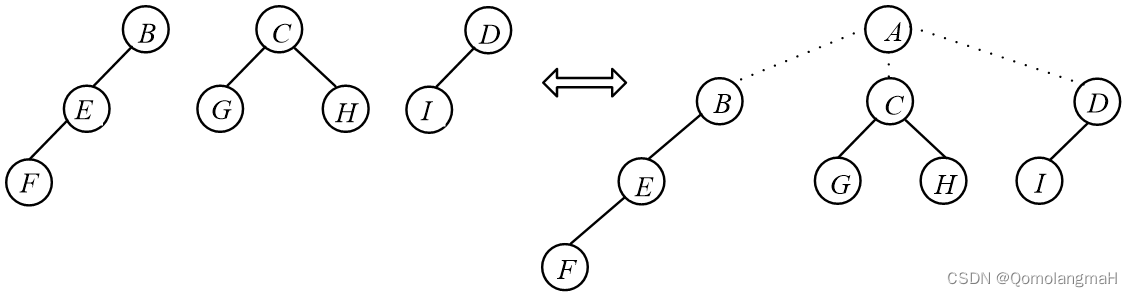
5. 左儿子右兄弟链接结构
【数据结构】树与二叉树(十九):树的存储结构——左儿子右兄弟链接结构(树、森林与二叉树的转化)
左儿子右兄弟链接结构通过使用每个节点的三个域(FirstChild、Data、NextBrother)来构建一棵树,同时使得树具有二叉树的性质。具体来说,每个节点包含以下信息:
- FirstChild: 存放指向该节点的大儿子(最左边的子节点)的指针。这个指针使得我们可以迅速找到一个节点的第一个子节点。
- Data: 存放节点的数据。
- NextBrother: 存放指向该节点的大兄弟(同一层中右边的兄弟节点)的指针。这个指针使得我们可以在同一层中迅速找到节点的下一个兄弟节点。
通过这样的结构,整棵树可以用左儿子右兄弟链接结构表示成一棵二叉树。这种表示方式有时候被用于一些特殊的树结构,例如二叉树、二叉树的森林等。这种结构的优点之一是它更紧凑地表示树,而不需要额外的指针来表示兄弟关系。
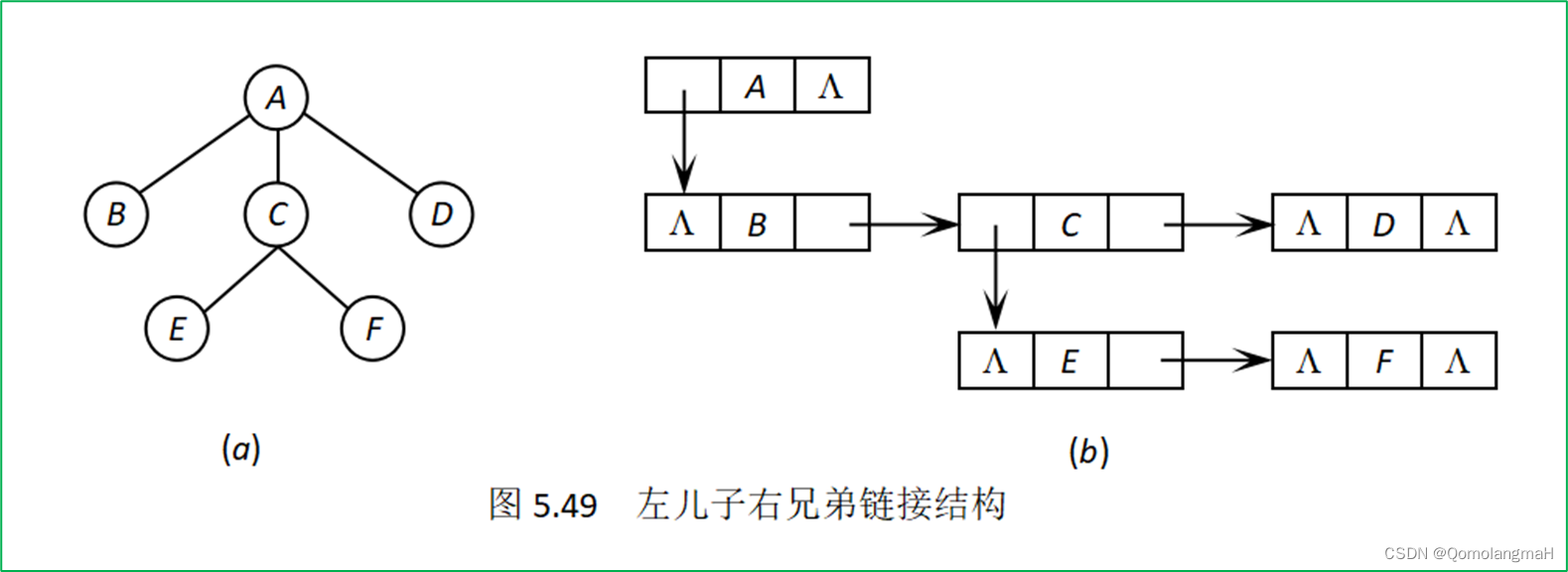
A/|\B C D/ \E F
A
|
B -- C -- D|E -- F
即:
A/ B \C/ \ E D\F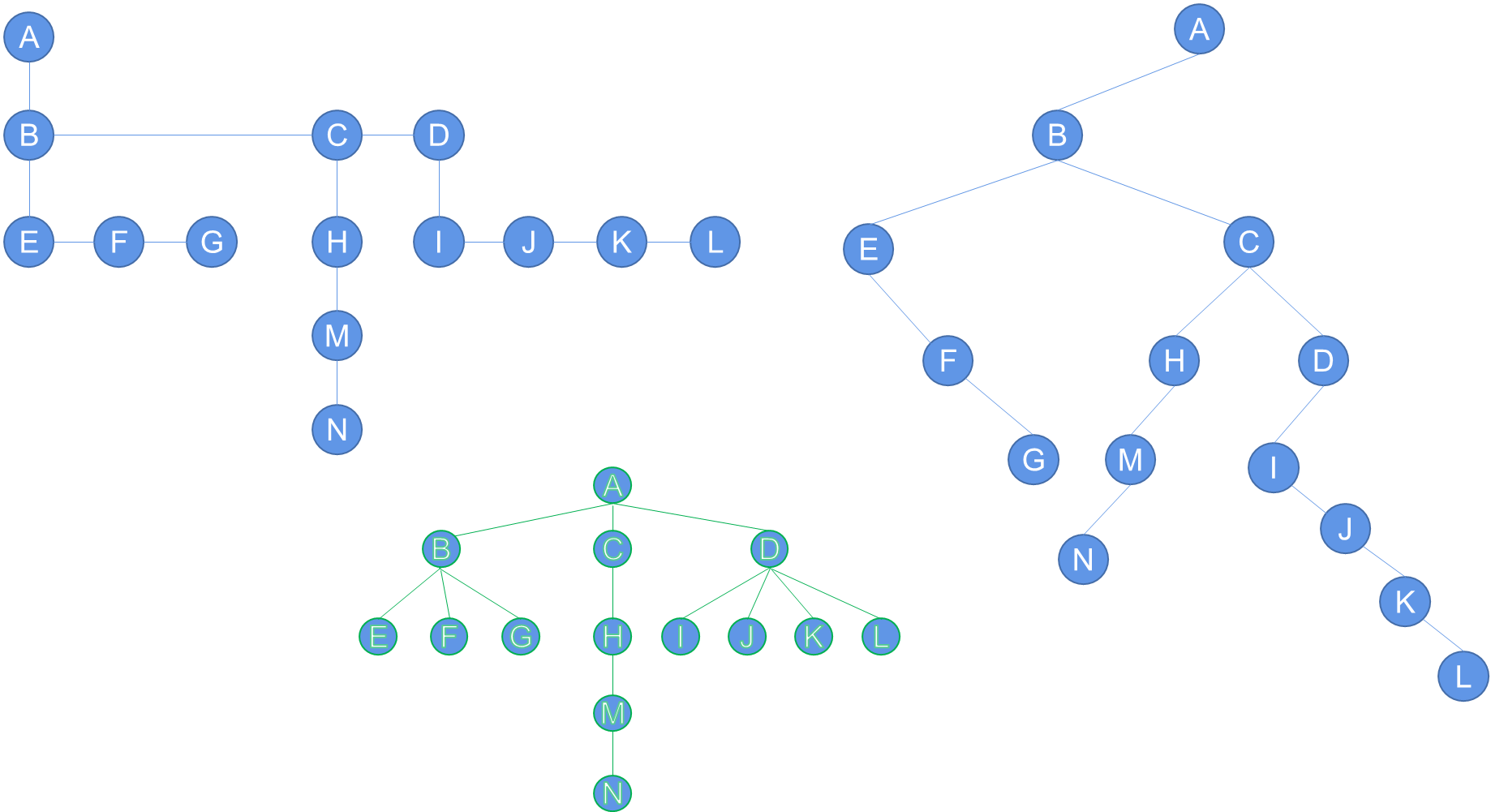
5.3.2 获取结点的算法
【数据结构】树与二叉树(二十):树获取大儿子、大兄弟结点的算法(GFC、GNB)
5.3.3 树和森林的遍历
【数据结构】树与二叉树(七):二叉树的遍历(先序、中序、后序及其C语言实现)
1. 先根遍历(递归、非递归)
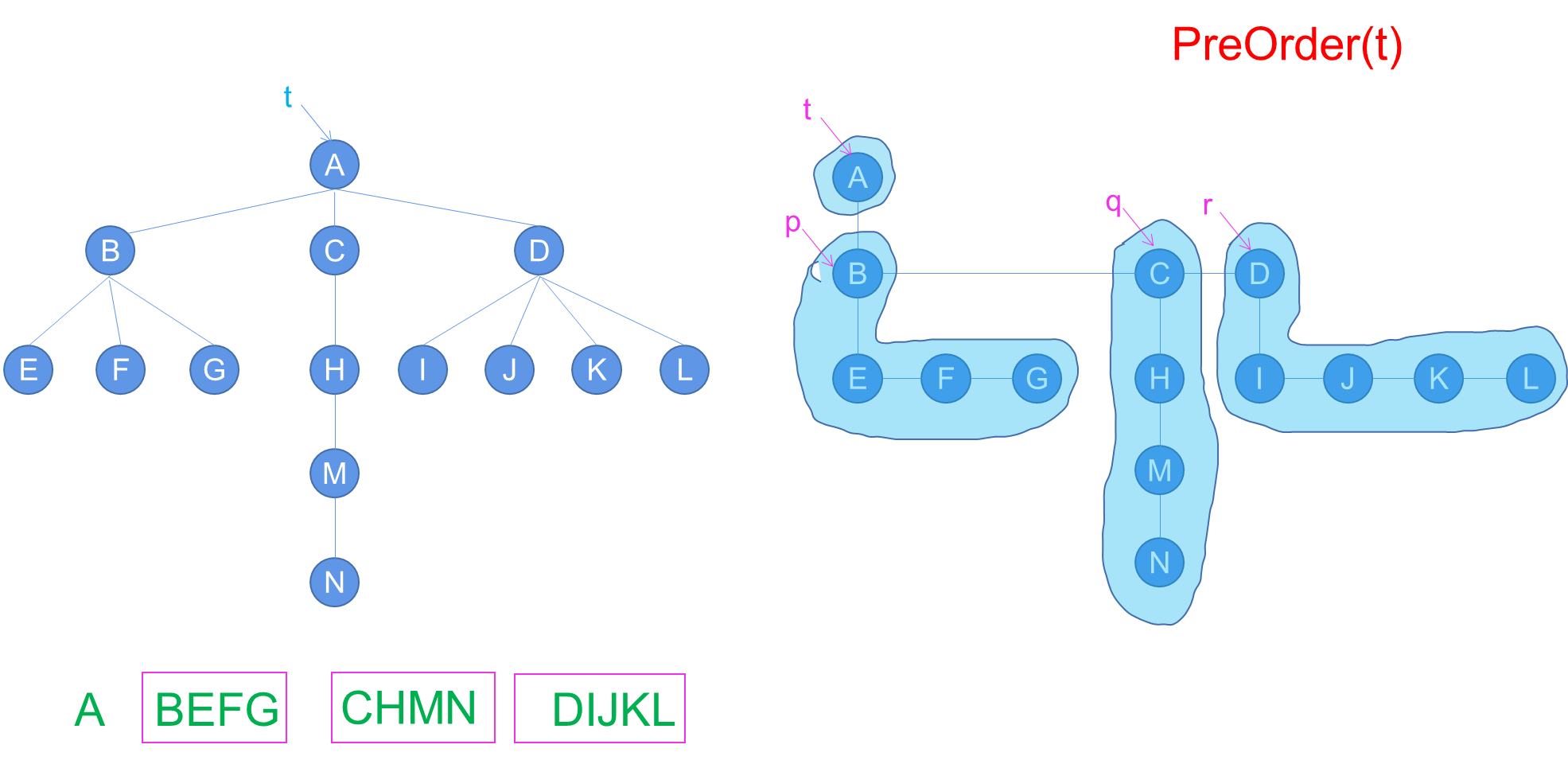
【数据结构】树与二叉树(廿一):树和森林的遍历——先根遍历(递归算法PreOrder、非递归算法NPO)
2. 后根遍历(递归)
a.理论
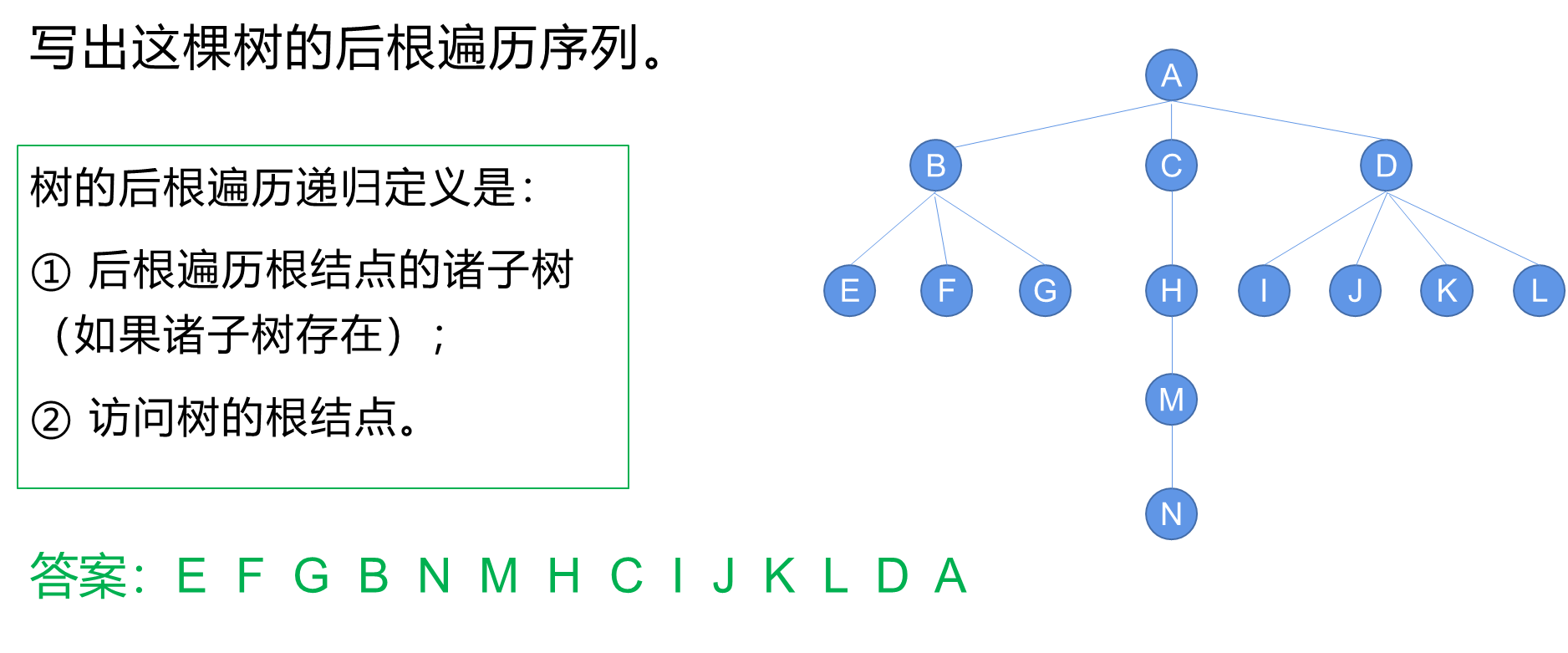
b. ADL算法PostOrder

-
基本条件检查:
IF t=NULL THEN RETURN.:如果树的根节点t为空,直接返回,递归的出口条件。
-
递归调用子树的后根遍历:
PostOrder(t.child).:递归调用后根遍历算法,对当前节点t的第一个孩子进行遍历。
-
迭代调用右兄弟节点的后根遍历:
WHILE child≠∧ DO:使用WHILE循环,判断当前节点的第一个孩子是否存在(child≠∧)。PostOrder(child).:递归调用先根遍历算法,对当前节点child进行遍历。GNB(child.child).:调用算法GNB获取当前节点child的下一个兄弟节点,然后继续遍历。
-
打印根节点数据:
PRINT(Data(t)).:打印当前树节点t的数据。
通过递归地调用后根遍历算法,依次访问树的根节点、根节点的孩子节点、孩子节点的兄弟节点……以此类推,完成对整个树的后根遍历。
c. 代码实现
void PostOrder(TreeNode* t) {if (t == NULL) {return;}// 递归调用子树的后根遍历TreeNode* child = getFirstChild(t);while (child != NULL) {PostOrder(child);// 迭代调用右兄弟节点的后根遍历child = getNextBrother(child);}// 打印当前树节点的数据printf("%c ", t->data);
}3. 后根遍历(非递归)
a. ADL算法NPO
b. NPO算法解析
暂时仅提供c语言代码,ADL语言及代码解析,有缘再见……
c. 代码实现
// 后根遍历的非递归算法
void NorecPostOrder(TreeNode* root) {if (root == NULL) {return;}TreeNode* stack1[100];TreeNode* stack2[100];int top1 = -1;int top2 = -1;TreeNode* p = root;stack1[++top1] = p;while (top1 != -1) {p = stack1[top1--];stack2[++top2] = p;TreeNode* child = getFirstChild(p);while (child != NULL) {stack1[++top1] = child;child = getNextBrother(child);}}while (top2 != -1) {printf("%c ", stack2[top2--]->data);}
}-
参数:
root: 树的根节点。
-
局部变量:
stack[100]: 用于模拟栈的数组,存储待访问的节点。
3. 森林的遍历

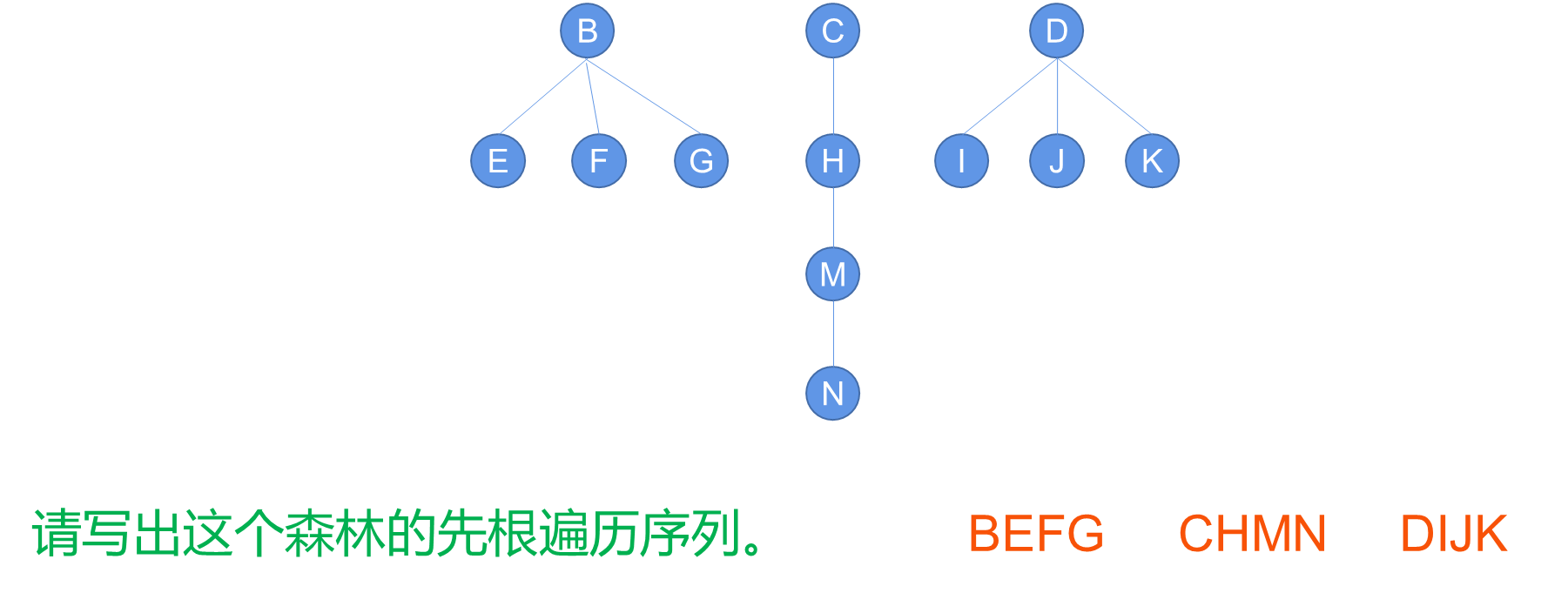
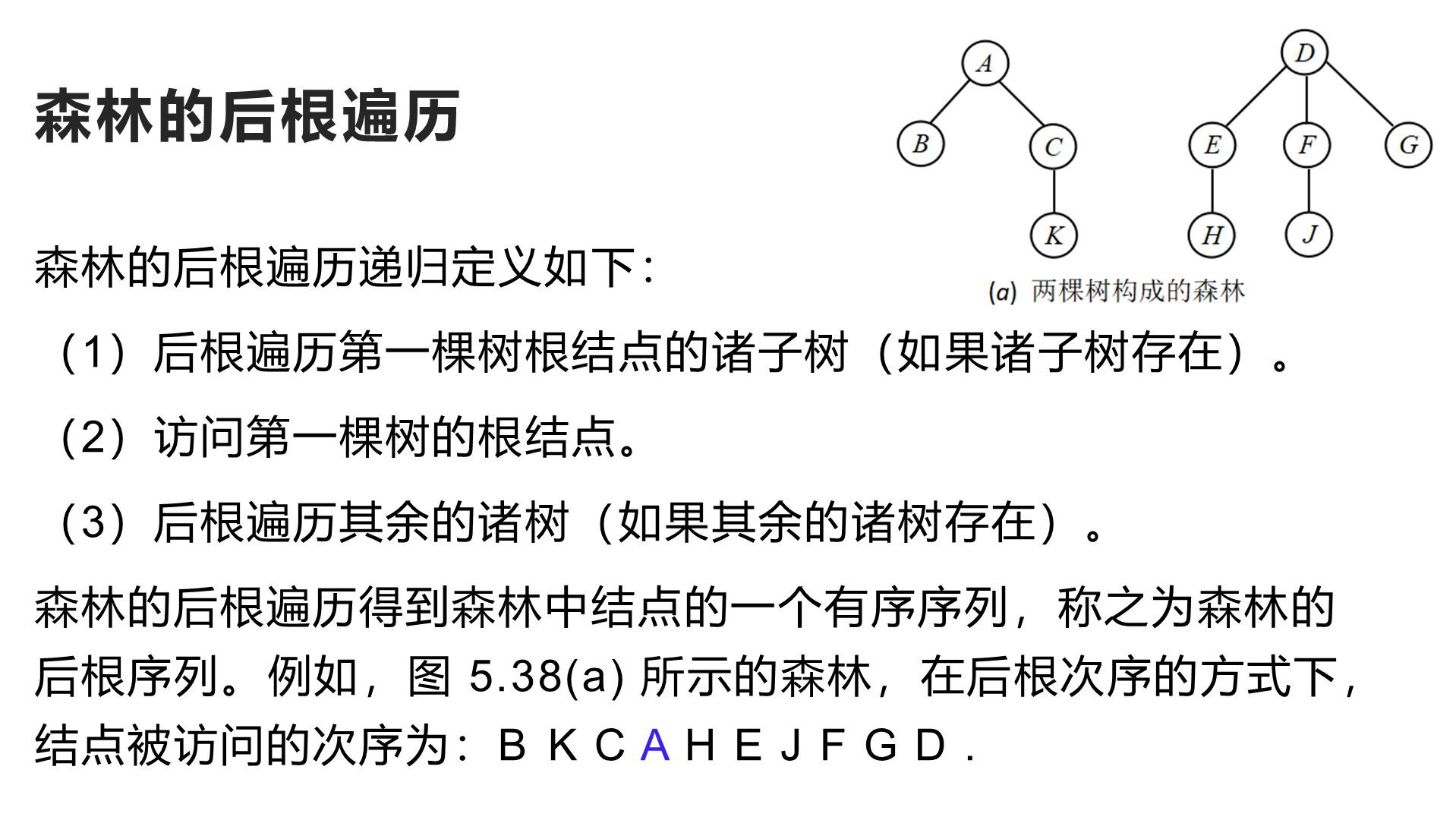
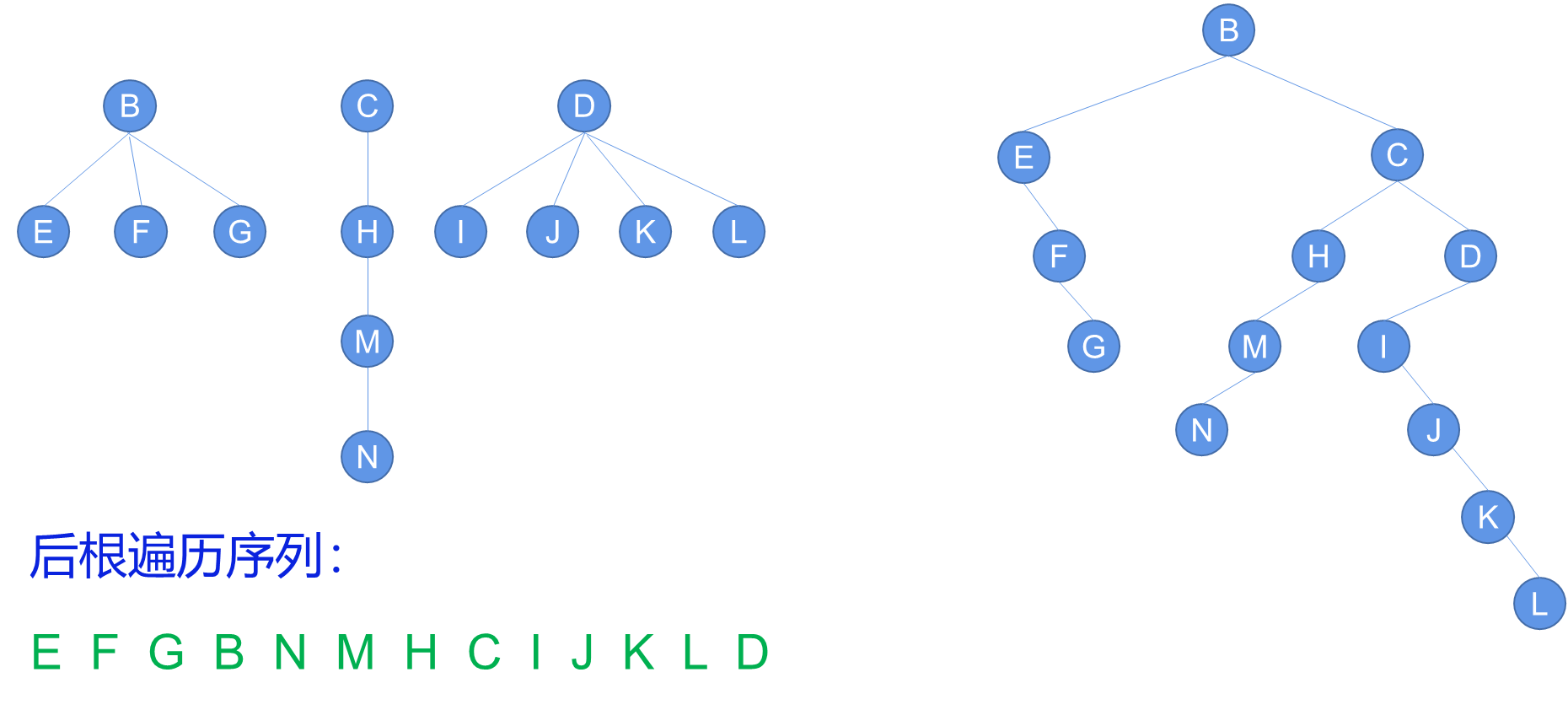
4. 代码整合
#include <stdio.h>
#include <stdlib.h>// 定义树节点
typedef struct TreeNode {char data;struct TreeNode* firstChild;struct TreeNode* nextBrother;
} TreeNode;// 创建树节点
TreeNode* createNode(char data) {TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));if (newNode != NULL) {newNode->data = data;newNode->firstChild = NULL;newNode->nextBrother = NULL;}return newNode;
}// 释放树节点及其子树
void freeTree(TreeNode* root) {if (root != NULL) {freeTree(root->firstChild);freeTree(root->nextBrother);free(root);}
}// 算法GFC:获取大儿子结点
TreeNode* getFirstChild(TreeNode* p) {if (p != NULL && p->firstChild != NULL) {return p->firstChild;}return NULL;
}// 算法GNB:获取下一个兄弟结点
TreeNode* getNextBrother(TreeNode* p) {if (p != NULL && p->nextBrother != NULL) {return p->nextBrother;}return NULL;
}/* 使用已知的getFirstChild和getNextBrother函数实现后根遍历以t为根指针的树。*/
void PostOrder(TreeNode* t) {if (t == NULL) {return;}// 递归调用子树的后根遍历TreeNode* child = getFirstChild(t);while (child != NULL) {PostOrder(child);// 迭代调用右兄弟节点的后根遍历child = getNextBrother(child);}// 打印当前树节点的数据printf("%c ", t->data);
}// 后根遍历的非递归算法
void NorecPostOrder(TreeNode* root) {if (root == NULL) {return;}TreeNode* stack1[100];TreeNode* stack2[100];int top1 = -1;int top2 = -1;TreeNode* p = root;stack1[++top1] = p;while (top1 != -1) {p = stack1[top1--];stack2[++top2] = p;TreeNode* child = getFirstChild(p);while (child != NULL) {stack1[++top1] = child;child = getNextBrother(child);}}while (top2 != -1) {printf("%c ", stack2[top2--]->data);}
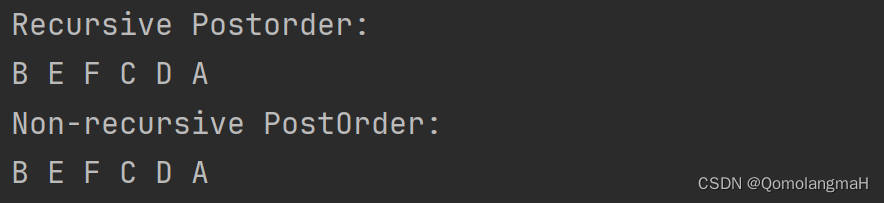
}int main() {// 构建左儿子右兄弟链接结构的树TreeNode* A = createNode('A');TreeNode* B = createNode('B');TreeNode* C = createNode('C');TreeNode* D = createNode('D');TreeNode* E = createNode('E');TreeNode* F = createNode('F');A->firstChild = B;B->nextBrother = C;C->nextBrother = D;C->firstChild = E;E->nextBrother = F;// 使用递归后根遍历算法printf("Recursive Postorder: \n");PostOrder(A);printf("\n");// 使用非递归后根遍历算法printf("Non-recursive PostOrder: \n");NorecPostOrder(A);printf("\n");// 释放树节点freeTree(A);return 0;
}
相关文章:

【数据结构】树与二叉树(廿二):树和森林的遍历——后根遍历(递归算法PostOrder、非递归算法NPO)
文章目录 5.1 树的基本概念5.1.1 树的定义5.1.2 森林的定义5.1.3 树的术语 5.2 二叉树5.3 树5.3.1 树的存储结构1. 理论基础2. 典型实例3. Father链接结构4. 儿子链表链接结构5. 左儿子右兄弟链接结构 5.3.2 获取结点的算法5.3.3 树和森林的遍历1. 先根遍历(递归、非…...
-安全管控之防暴露、限制访问、防DDos攻击、防爬虫、防非法引用)
精通Nginx(17)-安全管控之防暴露、限制访问、防DDos攻击、防爬虫、防非法引用
安全是每个系统都需要考虑的关键因素,Nginx在这方面提供了丰富的功能,使我们可以就实际情形做很精细调整。这些功能包括防信息暴露、客户端访问限制、通讯加密、防DDos攻击、防爬虫、防非法引用及防非法域名请求等。 目录 防信息暴露 关闭版本号 关闭目录列表 客户端访问…...
STM32 Flash
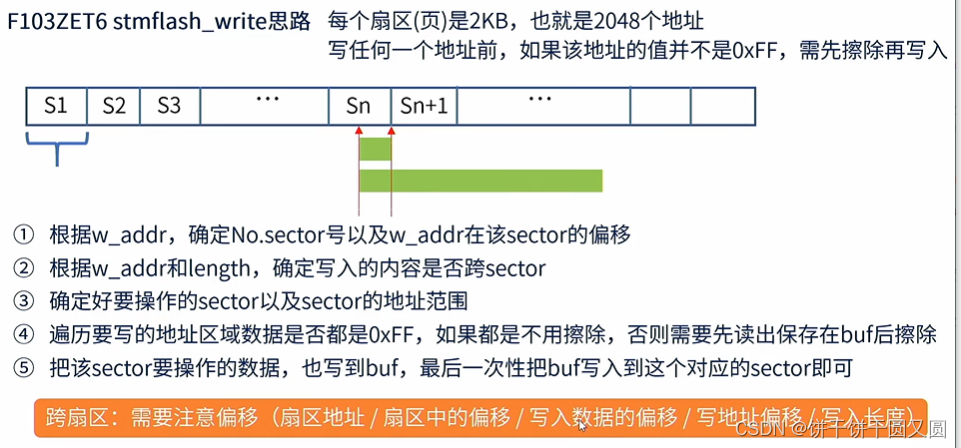
FLASH简介 Flash是常用的用于存储数据的半导体器件,它具有容量大,可重复擦写,按“扇区/块”擦除、掉电后数据可继续保存的特性。 常见的FLASH主要有NOR FLASH和NAND FLASH两种类型。NOR和NAND是两种数字门电路,可以简单地认为FL…...

文件批量重命名技巧:图片文件名太长怎么办?告别手动改名方法
在日常生活中,常常会遇到文件名过长导致的问题。尤其是在处理大量图片文件时,过长的文件名可能会使得文件管理变得混乱不堪。现在来看下云炫文件管理器如何批量重命名,让图片文件名变得更简洁,提高工作效率。 操作1、在云炫文件…...

微信小程序手写滑动tab
微信小程序手写滑动tab index.wxml <view class"tab-bar"> <scroll-view scroll-x class"tab-scroll"> <block wx:for"{{tabs}}" wx:key"index"> <view class"tab-item {{currentIndex index ? acti…...

一文读懂如何安全地存储密码
目录 引言 明文存储 基本哈希存储 加盐哈希存储 适应性哈希算法 密码加密存储 小结 引言 密码是最常用的身份验证手段,既简单又高效。密码安全是网络安全的基石,对保护个人和组织信息的安全具有根本性的作用。然而有关密码泄漏的安全问题一再发生…...
buffer和cache的区别)
【运维面试100问】(六)buffer和cache的区别
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...

创建域名邮箱邮件地址的方法与步骤
如何创建域名邮箱邮件地址?使用Zoho Mail创建域名邮箱邮件地址的步骤简单易懂,操作便捷。从其他邮箱迁移到Zoho Mail的过程也相当顺畅,您可以轻松为所有员工创建具有企业邮箱域名的电子邮件地址。 步骤1:添加并验证您的域名 首先,…...
)
Qt框架学习(1)
1.安装Qt官网 安装需注意的是,要安装开源版(有钱当我没说),而安装包都是一样的,主要是在注册账户时选择个人开发,而不要选公司,否则在安装时登录账号后会安装商业版Qt. 2.Qt中的快捷键 快捷键解释F4头文件和实现文件切换ShiftF…...
3D电路板在线渲染案例
从概念上讲,这是有道理的,因为PCB印制电路板上的走线从一个连接到下一个连接的路线基本上是平面的。 然而,我们生活在一个 3 维世界中,能够以这种方式可视化电路以及相应的组件,对于设计过程很有帮助。本文将介绍KiCad中基本的3D查看功能,以及如何使用NSDT 3DConvert在线…...
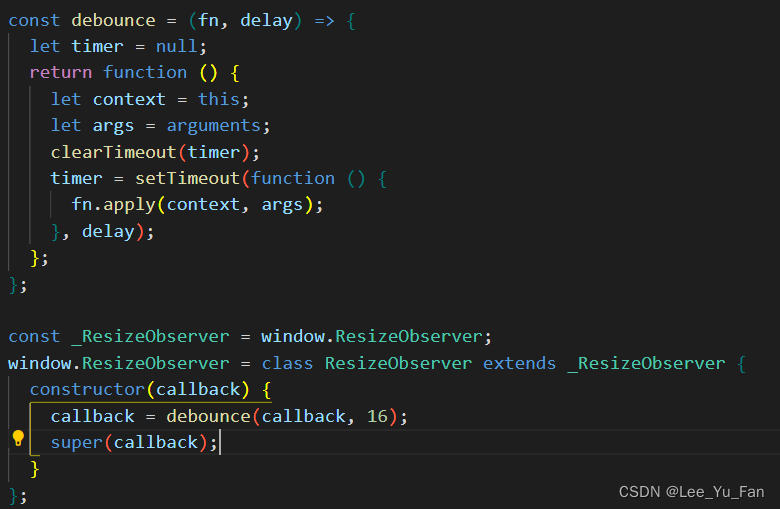
ResizeObserver loop limit exceeded报错解决方案
前言: 控制台没有报错,但是开发Vue项目过程中一直报ResizeObserver loop limit exceeded 错,找到以下解决方式。在main.js文件中重写 ResizeObserver 方法。 main.js文件 (完整版) import { createApp } from "v…...

【OpenCV实现图像:使用OpenCV进行图像处理之透视变换】
文章目录 概要计算公式举个栗子实际应用小结 概要 透视变换(Perspective Transformation)是一种图像处理中常用的变换手段,它用于将图像从一个视角映射到另一个视角,常被称为投影映射。透视变换可以用于矫正图像中的透视畸变&…...

Vue中学习笔记-数据代理
文章目录 前文提要数据代理的概念MVVM模型和Vue中的数据代理M,模型V,视图VM,视图模型 前文提要 本人仅做个人学习记录,如有错误,请多包涵 数据代理的概念 使用一个对象代理对另一个对象中属性的操作。 MVVM模型和Vu…...
IDEA 配置maven结合案例使用篇
1. 项目需求和结构分析 需求案例:搭建一个电商平台项目,该平台包括用户服务、订单服务、通用工具模块等。 项目架构: 用户服务:负责处理用户相关的逻辑,例如用户信息的管理、用户注册、登录等。 spring-context 6.0.…...

基于白鲸算法优化概率神经网络PNN的分类预测 - 附代码
基于白鲸算法优化概率神经网络PNN的分类预测 - 附代码 文章目录 基于白鲸算法优化概率神经网络PNN的分类预测 - 附代码1.PNN网络概述2.变压器故障诊街系统相关背景2.1 模型建立 3.基于白鲸优化的PNN网络5.测试结果6.参考文献7.Matlab代码 摘要:针对PNN神经网络的光滑…...
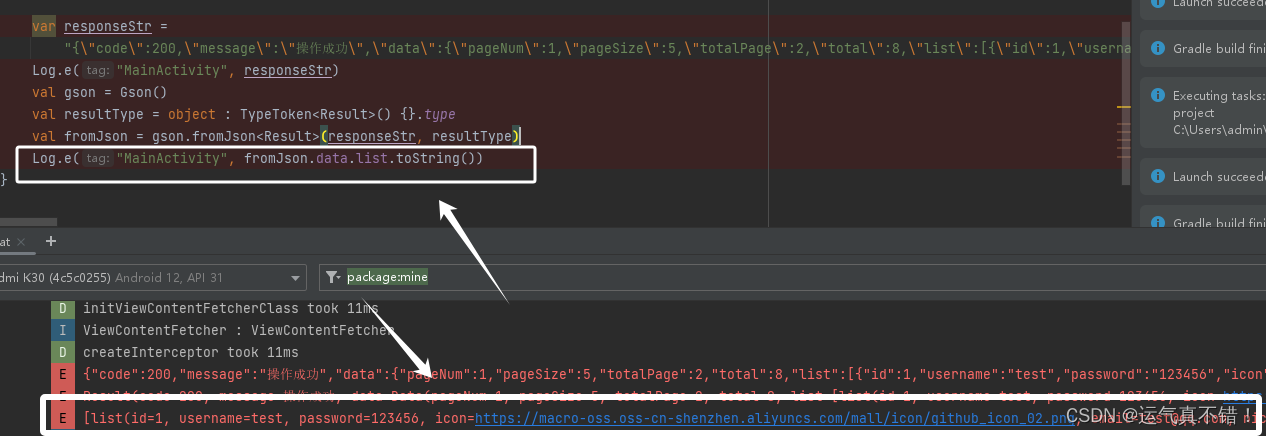
Android使用Kotlin利用Gson解析多层嵌套Json数据
文章目录 1、依赖2、解析 1、依赖 build.gradle(app)中加入 dependencies { implementation com.google.code.gson:gson:2.8.9 }2、解析 假设这是要解析Json数据 var responseStr "{"code": 200,"message": "操作成功","data&quo…...

DOM事件的传播机制
DOM事件的传播机制是指当一个事件在DOM树中触发时,它是如何在各个元素之间传播的。DOM事件传播机制分为三个阶段:捕获阶段、目标阶段和冒泡阶段。此外,还有一种常用的技术称为事件委托,它能够简化事件处理程序的绑定和管理。本文将…...
gitlab利用CI多工程持续构建
搭建CI的过程中有多个工程的时候,一个完美的构建过程往往是子工程上的更新(push 或者是merge)触发父工程的构建,这就需要如下建立一个downstream pipeline 子仓库1 .gitlab-ci.yml stages:- buildbuild_job:stage: buildtrigger:project: test_user/tes…...

【C++初阶】四、类和对象(构造函数、析构函数、拷贝构造函数、赋值运算符重载函数)
相关代码gitee自取: C语言学习日记: 加油努力 (gitee.com) 接上期: 【C初阶】三、类和对象 (面向过程、class类、类的访问限定符和封装、类的实例化、类对象模型、this指针) -CSDN博客 引入:类的六个默认成员函数…...

js粒子效果(二)
效果: 代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Particle Animation</title><…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
