acwing算法基础之数学知识--求卡特兰数
目录
- 1 基础知识
- 2 模板
- 3 工程化
1 基础知识
题目:给定n个0和n个1,它们将按照某种顺序排成长度为2n的序列,求它们能排成的所有序列中,能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个?
输出的答案对 1 0 9 + 7 10^9+7 109+7取模。
原题目等价于,
在平面直角坐标系xoy下,起点为(0,0),终点为(n,n),每次只能向上走一格或向右走一格,问从起点走到终点,且路径上横坐标大于等于纵坐标恒成立,求有多少种走法?
用下图表示即为,
在不触碰到红线(即 y = x + 1 y=x+1 y=x+1)的情况下,从起点(0,0)走到终点(n,n),有多少种走法。

考虑一种触碰到红线,走到终点(n,n)的路径,如下图粗蓝色所显示路径。我们将从首次触碰到红线的点,记作红点。那么,将接下来的路径按照红线( y = x + 1 y=x+1 y=x+1)对称,可以得到粗绿色所显示路径,最终走到点(n-1,n+1)。

也就是说,任何一条触碰红线,走到终点(n,n)的路径,都可以等效成,一条走到(n-1,n+1)的路径。而从起点走到点(n-1,n+1)的路径数为 C 2 n n − 1 C_{2n}^{n-1} C2nn−1,故触碰红线走到终点的路径数目为 C 2 n n − 1 C_{2n}^{n-1} C2nn−1。
题目要计算的是,不触碰红线走到终点(n,n)的路径数目,它等于总路径数目减去触碰红线走到终点(n,n)的路径数目,即答案可计算如下,
C 2 n n − C 2 n n − 1 = ( 2 n ) ! n ! ⋅ n ! − ( 2 n ) ! ( n − 1 ) ! ⋅ ( n + 1 ) ! C_{2n}^n-C_{2n}^{n-1}=\frac{(2n)!}{n!\cdot n!} - \frac{(2n)!}{(n-1)!\cdot (n+1)!} C2nn−C2nn−1=n!⋅n!(2n)!−(n−1)!⋅(n+1)!(2n)!
= ( 2 n ) ! ( n − 1 ) ! ⋅ n ! ⋅ ( 1 n − 1 n + 1 ) = ( 2 n ) ! ( n − 1 ) ! ⋅ n ! ⋅ 1 n ( n + 1 ) =\frac{(2n)!}{(n-1)!\cdot n!}\cdot (\frac{1}{n} - \frac{1}{n+1})=\frac{(2n)!}{(n-1)!\cdot n!}\cdot \frac{1}{n(n+1)} =(n−1)!⋅n!(2n)!⋅(n1−n+11)=(n−1)!⋅n!(2n)!⋅n(n+1)1
= ( 2 n ) ! n ! ⋅ n ! ⋅ 1 n + 1 = C 2 n n n + 1 =\frac{(2n)!}{n!\cdot n!} \cdot \frac{1}{n+1}=\frac{C_{2n}^n}{n+1} =n!⋅n!(2n)!⋅n+11=n+1C2nn
其中 C 2 n n n + 1 \frac{C_{2n}^{n}}{n+1} n+1C2nn即为卡特兰数。
转换为代码,如下,
#include <iostream>using namespace std;const int mod = 1e9 + 7;int qmi(int a, int k, int p) {int res = 1;while (k) {if (k & 1) res = (long long)res * a % p;k >>= 1;a = (long long)a * a % p;}return res;
}int main() {int n;cin >> n;//计算C[2 * n][n] / (n + 1) % modint res = 1;for (int i = 1, j = 2 * n; i <= n; ++i, --j) {res = (long long)res * j % mod;res = (long long)res * qmi(i, mod - 2, mod) % mod;} res = (long long)res * qmi(n + 1, mod - 2, mod) % mod;cout << res << endl;return 0;
}
2 模板
暂无。。。
3 工程化
暂无。。。
相关文章:

acwing算法基础之数学知识--求卡特兰数
目录 1 基础知识2 模板3 工程化 1 基础知识 题目:给定n个0和n个1,它们将按照某种顺序排成长度为2n的序列,求它们能排成的所有序列中,能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个? 输出的答案对 1 0 …...
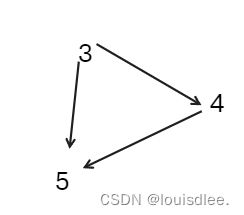
《洛谷深入浅出基础篇》P4017最大食物链————拓扑排序
上链接:P4017 最大食物链计数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P4017 上题干: 题目背景 你知道食物链吗?Delia 生物考试的时候,数食物链条数的题目全都错了,因为她总是…...
设置定时自动请求测试_自动定时循环发送http_post请求---postman工作笔记001
其实就是创建接口文件夹的时候,有个monitor collection 用来监听接口执行情况,这里就可以设置 可以看到多久执行一次对吧,这里可以设置每几分钟执行一次,一共执行多少次等等 但是这里要说明一下,如果需要使用monitor功能,必须需要登录, 所以如果这里点击monitor collection…...

Vue3封装全局插件
定义一个全局加载组件 一、首先定义dom元素 定义一个index.vue文件 <template><div class"loading">loading...</div> </template> <script setup lang"ts"></script> <style scoped> .loading {display: fl…...

【Python 训练营】N_6 求素数
题目 判断101-200之间有多少个素数,并输出所有素数。 分析 判断素数的方法:用一个数分别去除2到sqrt(这个数),如果能被整除,则表明此数不是素数,反之是素数。 答案 h 0 leap 1 from math import sqrt from sys …...
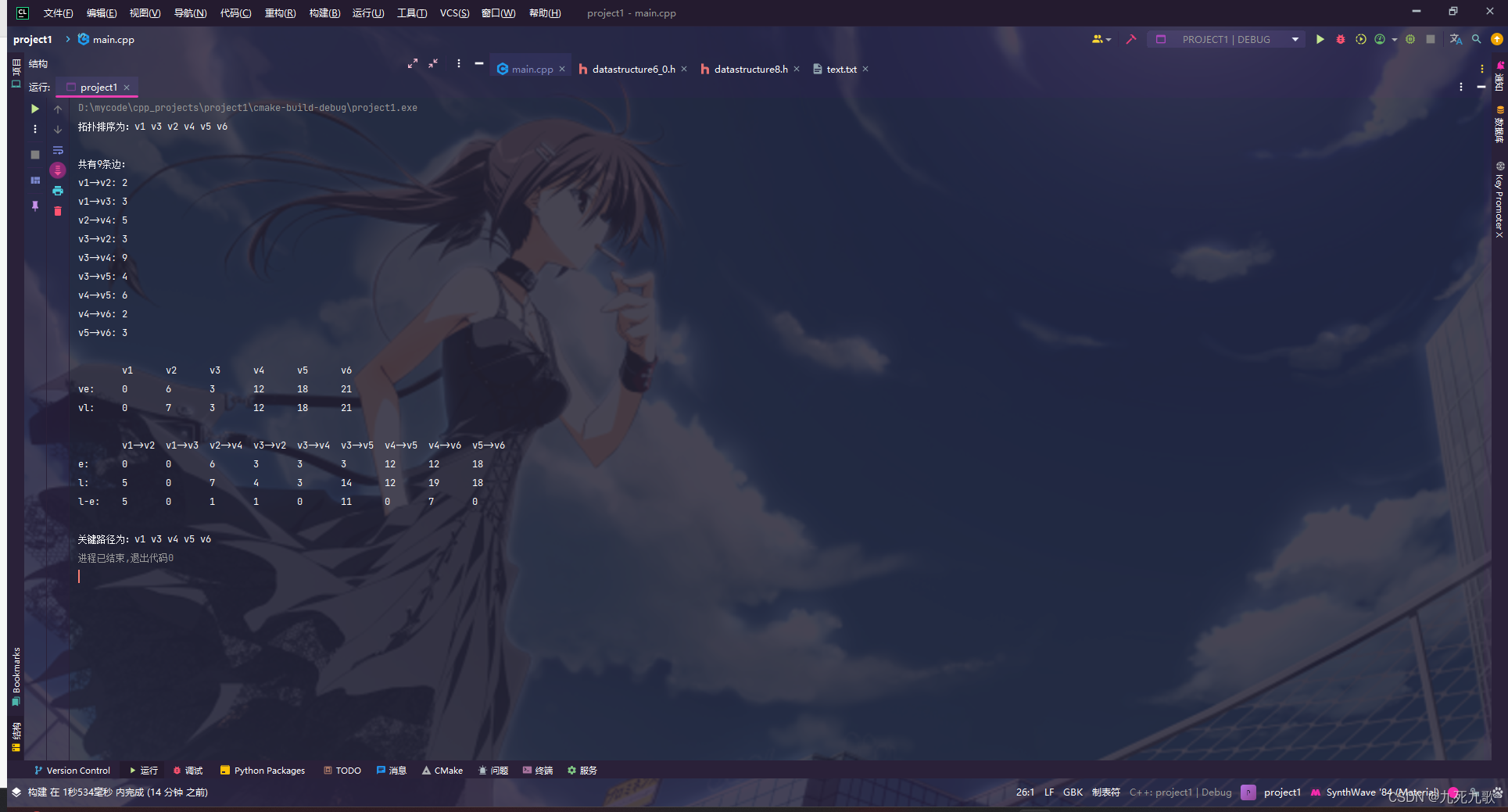
【图论】关键路径求法c++
代码结构如下图: 其中topologicalSort(float**, int, int*, bool*, int, int)用来递归求解拓扑排序,topologicalSort(float**, int*&, int, int, int)传参图的邻接矩阵mat与结点个数n,与一个引用变量数组topo,返回一个布尔值…...

基于51单片机电子钟万年历LCD1602显示
51单片机的电子钟万年历LCD1602显示 🔴 🔵51单片机的电子钟万年历LCD1602显示🔴 🔵主要功能:🔴 🔵讲解视频🔴 🔵仿真图:🔴 🔵程序&…...
时间复杂度和运算
时间复杂度 在算法和数据结构中,有许多时间复杂度比 O(1) 更差的情况。以下是一些常见的时间复杂度,按照从最优到最差的顺序排列: O(1): 常数时间复杂度,操作的运行时间与输入规模无关,是最理想的情况。 O…...

深入Tailwind CSS中的文本样式
深入Tailwind CSS中的文本样式 样式文本是网页设计的一个基本组成部分,而 Tailwind CSS 提供了范围广泛的实用类,使文本样式设计既高效又有效。 在本本中,我们将探索文本样式的常见最佳实践,讨论潜在的陷阱,并推荐设计方法。我们…...
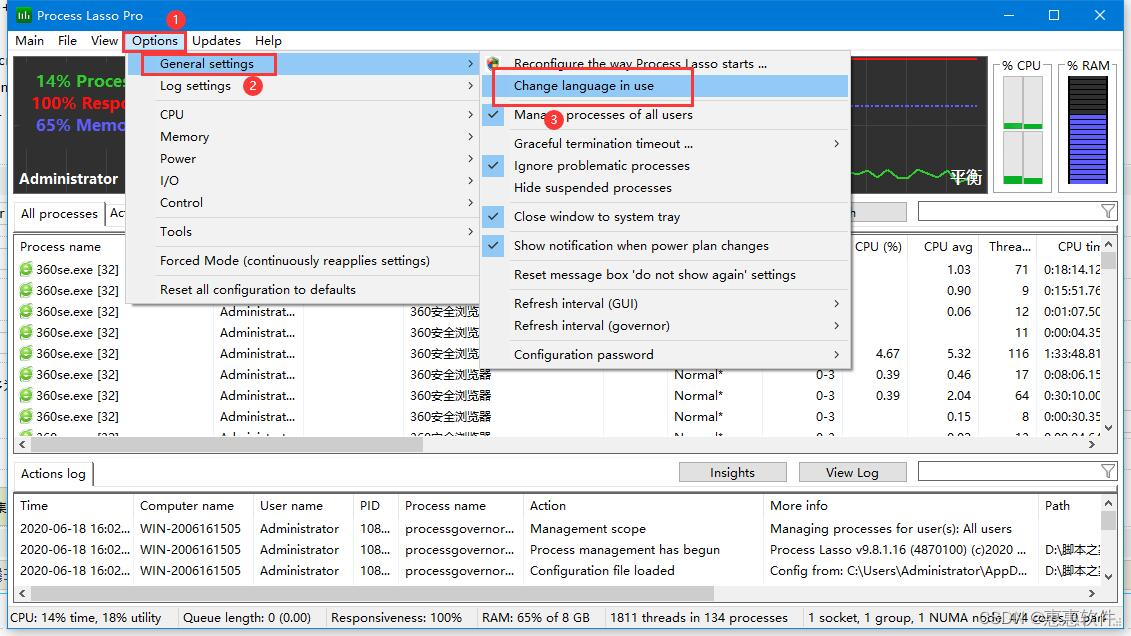
系统优化软件Bitsum Process Lasso Pro v12.4,供大家学习研究参考
1、自动或手动调整进程优先级;将不需要抑制的进程添加到排除列表; 2、设置动态提升前台运行的进程/线程的优先级 3、设置进程黑名单,禁止无用进程(机制为启动即结束,而非拦截其启动)。 4、优化I/O优先级以及电源模式自动化。 5、ProBalance功能。翻译成中文是“进程平衡…...

敏捷DevOps专家王立杰:端到端DevOps持续交付的5P法则 | IDCF
今天有一个流行的英文缩写词用来刻画这个风云变幻的时代:VUCA(乌卡时代)。四个英文字母分别表示动荡性(Volatility)、不确定性(Uncertainty)、复杂性(Complexity)和模糊性…...

分布式锁详解
文章目录 分布式锁1. [传统锁回顾](https://blog.csdn.net/qq_45525848/article/details/134608044?csdn_share_tail%7B%22type%22:%22blog%22,%22rType%22:%22article%22,%22rId%22:%22134608044%22,%22source%22:%22qq_45525848%22%7D)1.1. 从减库存聊起1.2. 环境准备1.3. 简…...
——算术运算符)
Python入门学习篇(二)——算术运算符
1 算术运算符 1.1 分类 类型含义示例注意事项加号12➡3“12”“3"➡"123”数值之间,是加法运算(True为1,False为0)字符串之间,是进行拼接数值和字符串之间是不可以使用加法运算的,会报错-减号1-2➡-1*乘号2*3➡6/除法2/1➡2.0除法的结果永远为小数%取余10%2➡0//取…...
微软发布最新.NET 8长期支持版本,云计算、AI应用支持再强化
11 月 15 日开始的为期三天的 .NET Conf 在线活动的开幕日上,.NET 8作为微软的开源跨平台开发平台正式发布。.NET 团队着重强调云、性能、全栈 Blazor、AI 和 .NET MAUI 是.NET 8的主要亮点。.NET团队在 .NET Conf 2023 [1]活动开幕式上表示:“通过这个版…...
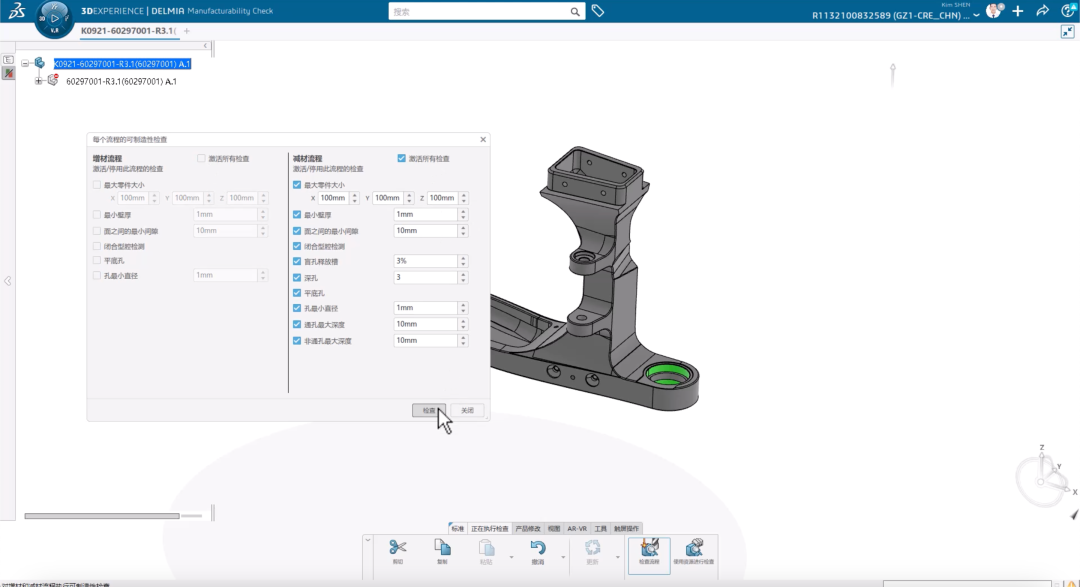
达索系统3DEXPERIENCE WORKS 2024 Fabrication新功能
当发现产品的制造环节,以及因产品模型本身的设计而导致制造环节存在不合理性,从而导致加工制造成本增加。 快速判断,轻松协作 在达索系统3DEXPERIENCE WORKS 2024中我们可以快速的判断产品的可制造性,以及快速与前端设计沟通协作…...

Web3与Web3.0: Web3指的是去中心化和基于区块链的网络,Web3.0指的是链接或语义网络。
目录 Web3与Web3.0: Web3指的是去中心化和基于区块链的网络 Web3.0指的是链接或语义网络。...

98、Text2Room: Extracting Textured 3D Meshes from 2D Text-to-Image Models
简介 github 利用预训练的2D文本到图像模型来合成来自不同姿势的一系列图像。为了将这些输出提升为一致的3D场景表示,将单目深度估计与文本条件下的绘画模型结合起来,提出了一个连续的对齐策略,迭代地融合场景帧与现有的几何形状࿰…...
)
MySQL 优化器 Index Condition Pushdown下推(ICP)
ICP 测试 准备数据 CREATE TABLE icp (employee_id int(6) NOT NULL AUTO_INCREMENT,first_name varchar(20) DEFAULT NULL,last_name varchar(25) DEFAULT NULL,email varchar(25) DEFAULT NULL,phone_number varchar(20) DEFAULT NULL,PRIMARY KEY (employee_id) );insert i…...
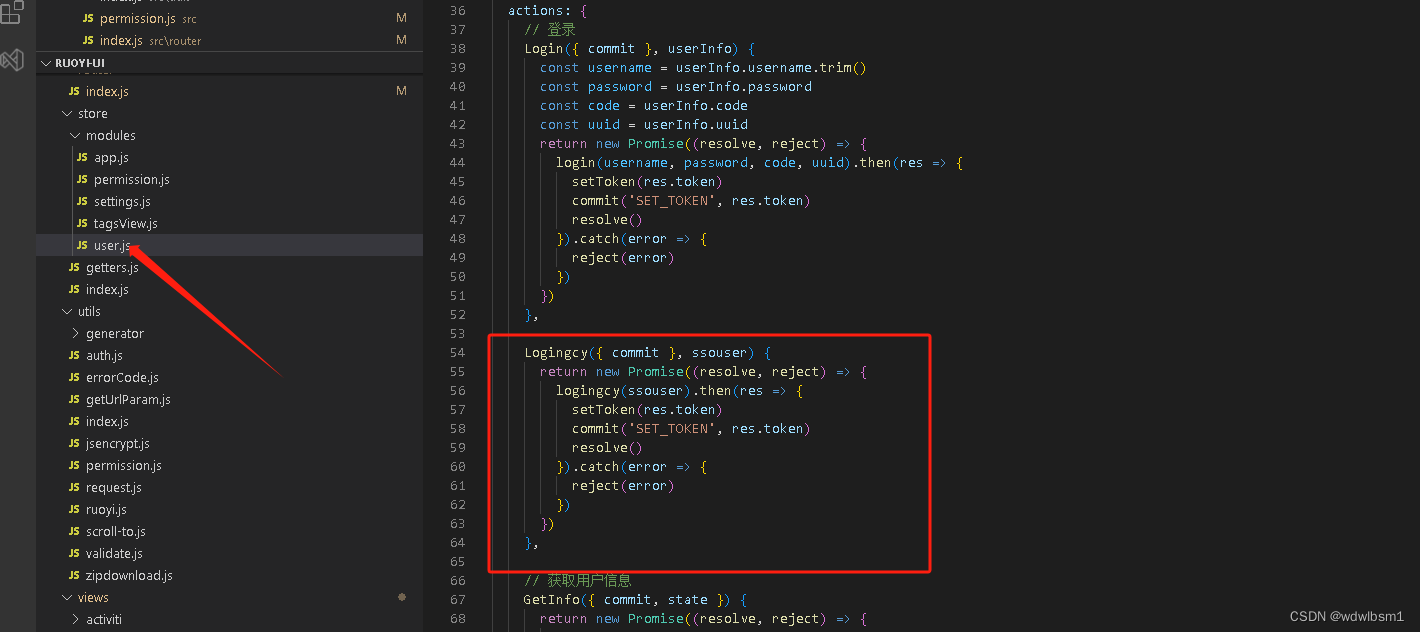
ruoyi 若依框架采用第三方登录
在项目中,前后端分离的若依项目,需要通过统一认证,或者是第三方协带认证信息跳转到本系统的指定页面。需要前后端都做相应的改造,由于第一次实现时已过了很久,再次重写时,发现还是搞了很长时间,…...

dom api
dom的全称为Document Object Model,即文档对象模型.所谓文档就是html页面,对象就是js里的对象,通过这个模型把页面上的元素和js里的对象关联起来. 下面是关于dom api的一些常用方法 1.获取元素 使用querySelector()方法获取一个元素 使用querySelectorAll()方法获取所有元素 当…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
