【图论】关键路径求法c++
代码结构如下图:

其中topologicalSort(float**, int, int*, bool*, int, int)用来递归求解拓扑排序,topologicalSort(float**, int*&, int, int, int)传参图的邻接矩阵mat与结点个数n,与一个引用变量数组topo,返回一个布尔值表示该图是否存在拓扑排序,同时将引用变量数组topo赋值为该图的拓扑序列。
getEdges(float**, int**&, int)传参图的邻接矩阵mat,引用变量二维数组edge,结点数n。然后将返回该图的边数,同时将float赋值为一个存储图的边的起点与终点的edgeNum * 2维的数组。
aoe(float**, int, int*&, int&, float*&, float*&, float*&, float*&, int*&, int**&, int&)分别传参邻接矩阵mat,结点数n,引用变量criticalPath表示关键路径,引用变量ve,vl,e,l正如名字所示,topo与edges表示拓扑序列与边,edgeNum表示边的数量。
aoe(float**, int, int*&, int&, float*&, float*&, float*&, float*&)与上一个函数差不多,只是少了topo与edges,edgeNum两个参数,并且多了一个布尔类型的返回值,返回的是关键路径是否存在。
aoe(float**, int*&, int&)则更是只有三个参数,他不对ve,vl,e,l进行返回。
aoe
static const float INF = 1.0f/0.0f;// x is what you are, and y is meaning to you are the no.y numbers to sort.
void topologicalSort(float** mat, int n, int* arr, bool* flags, int x=0, int y=0) {arr[y] = x;flags[x] = true;float tmp[n];// first, set all the elements of the no.x row to INF, and store the original value to tmp;// just like delete this vertexfor (int i = 0; i < n; ++i) {tmp[i] = mat[x][i];mat[x][i] = INF;}for (int i = 0; i < n; ++i) {int k = (x + i) % n;// if k have not recorded in arr.if (!flags[k]) {bool flag = true;// this loop is aim to find a vertex whose in_degree is equals to 0.for (int j = 0; j < n; ++j) {if (j != k && mat[j][k] != INF) {flag = false;break;}}// if you delete x, the in_degree of k is equals to 0. so do a recursive call.if (flag) {topologicalSort(mat, n, arr, flags, k, y+1);}}}// restore the no.x rowfor (int i = 0; i < n; ++i) {mat[x][i] = tmp[i];}}bool topologicalSort(float** mat, int* &topo, int n, int x=0, int y=0) {topo = new int[n];bool *flags = new bool[n];for (int i = 0; i < n; ++i) {flags[i] = false;}topologicalSort(mat, n, topo, flags, x, y);for (int i = 0; i < n; ++i) {if (!flags[i]) return false;}return true;}int getEdges(float** mat, int** &edges, int n) {// e is for the edges, whose account is unsure// ans is for the number of edgesint ans = 0;int** e = new int*[n * (n - 1)];for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j || mat[i][j] == INF) continue;e[ans++] = new int[]{i, j};}}// copy e into edgesedges = new int*[ans];for (int i = 0; i < ans; ++i) {edges[i] = e[i];}delete[] e;return ans;}void aoe(float** mat, int n, int* &criticalPath, int &length, float* &ve, float* &vl, float* &e, float* &l, int* &topo, int** &edges, int &edgeNum) {ve = new float[n];vl = new float[n];e = new float[edgeNum];l = new float[edgeNum];for (int i = 0; i < n; ++i) {ve[i] = 0;}for (int i = 1; i < n; ++i) {int max = i;for (int j = 0; j < i; ++j) {if (mat[topo[j]][topo[i]] == 0 || mat[topo[j]][topo[i]] == INF) continue;if (ve[topo[j]] + mat[topo[j]][topo[i]] > ve[topo[max]] + mat[topo[max]][topo[i]]) {max = j;}}ve[topo[i]] = ve[topo[max]] + mat[topo[max]][topo[i]];}for (int i = 0; i < n; ++i) {vl[i] = ve[topo[n - 1]];}for (int i = n - 2; i >= 0; --i) {int min = i;for (int j = i + 1; j < n; ++j) {if (mat[topo[i]][topo[j]] == 0 || mat[topo[i]][topo[j]] == INF) continue;if (vl[topo[j]] - mat[topo[i]][topo[j]] < vl[topo[min]] - mat[topo[i]][topo[min]]) {min = j;}}vl[topo[i]] = vl[topo[min]] - mat[topo[i]][topo[min]];}for (int i = 0; i < edgeNum; ++i) {e[i] = ve[edges[i][0]];l[i] = vl[edges[i][1]] - mat[edges[i][0]][edges[i][1]];}int* critical = new int[n];critical[0] = topo[0];length = 1;for (int i = 0; i < n; ++i) {critical[i] = -1;}for (int i = 0; i < edgeNum; ++i) {float le = l[i] - e[i];if (le < 1e-32) {critical[edges[i][0]] = edges[i][1];length++;}}criticalPath = new int[length];int p = 0;int q = 0;while (p != -1) {criticalPath[q++] = p;p = critical[p];}delete[] critical;}bool aoe(float** mat, int n, int* &criticalPath, int &length, float* &ve, float* &vl, float* &e, float* &l) {int* topo;int flag = topologicalSort(mat, topo, n);if (!flag) return false;int** edges;int edgeNum = getEdges(mat, edges, n);aoe(mat, n, criticalPath, length, ve, vl, e, l, topo, edges, edgeNum);return true;}bool aoe(float** mat, int n, int* &criticalPath, int &length) {float* ve;float* vl;float* e;float* l;return aoe(mat, n, criticalPath, length, ve, vl, e, l);}
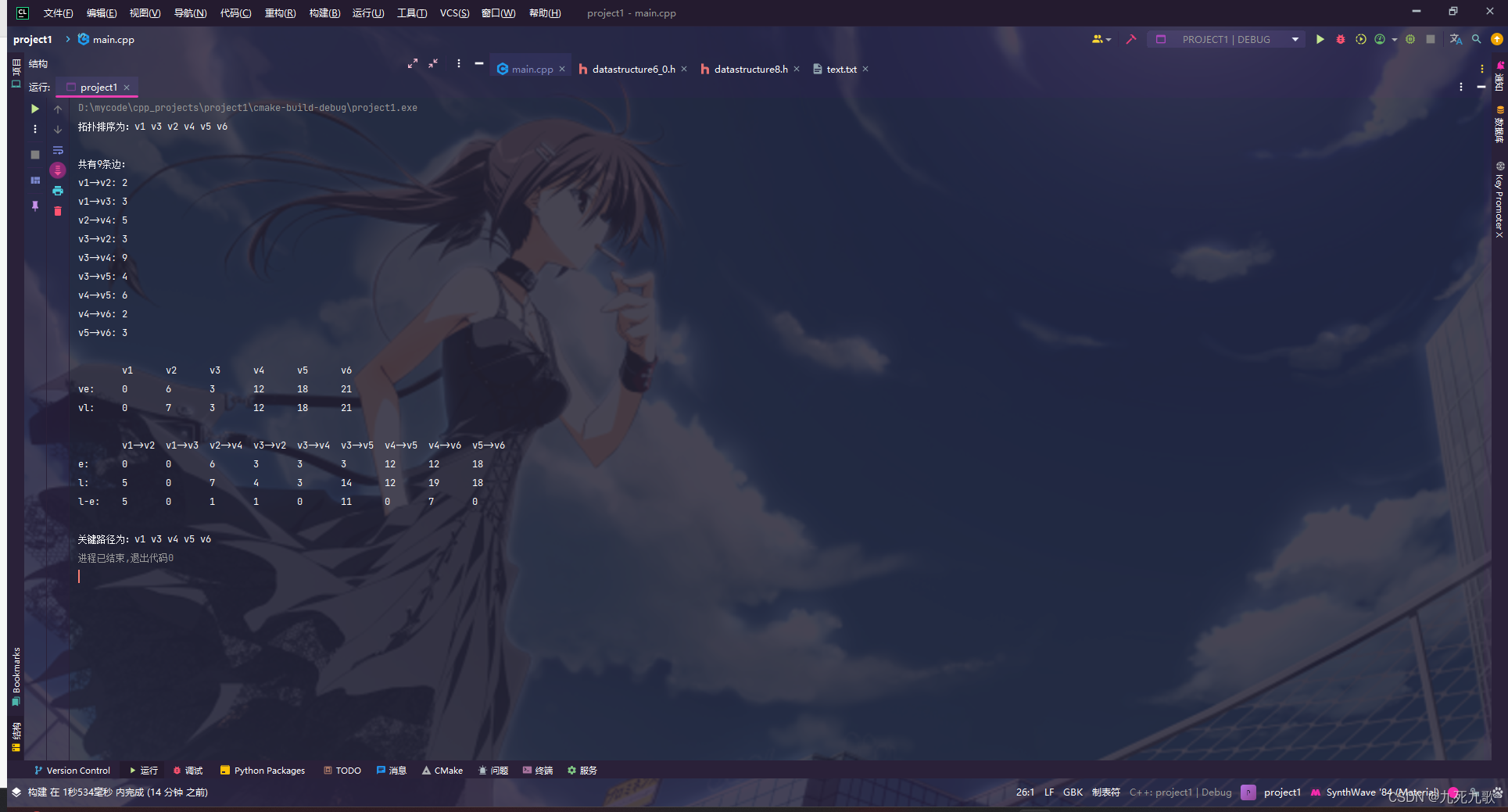
在main函数中进行一个测试,传参如下图:
int main() {int n = 6;float** mat = new float*[] {new float[] {0, 2, 3, INF, INF, INF },new float[] {INF, 0, INF, 5, INF, INF },new float[] {INF, 3, 0, 9, 4, INF },new float[] {INF, INF, INF, 0, 6, 2 },new float[] {INF, INF, INF, INF, 0, 3 },new float[] {INF, INF, INF, INF, INF, 0 }};char** value = new char*[n]{"v1", "v2", "v3", "v4", "v5", "v6"};float *ve, *vl, *e, *l;int* criticalPath;int length;int** edges;int* topo;topologicalSort(mat, topo, n);int edgeNum = getEdges(mat, edges, n);aoe(mat, n, criticalPath, length, ve, vl, e, l);cout << "拓扑排序为:";for (int i = 0; i < n; ++i) {cout << value[topo[i]] << " ";}cout << "\n\n";cout << "共有" << edgeNum << "条边:\n";for (int i = 0; i < edgeNum; ++i) {cout << value[edges[i][0]] << "->" << value[edges[i][1]] << ": " << mat[edges[i][0]][edges[i][1]] << endl;}cout << endl;for (int i = 0; i < n; ++i) {cout << '\t' << value[i];}cout << endl;cout << "ve:";for (int i = 0; i < n; ++i) {cout << '\t' << ve[i];}cout << endl;cout << "vl:";for (int i = 0; i < n; ++i) {cout << '\t' << vl[i];}cout << "\n\n";for (int i = 0; i < edgeNum; ++i) {cout << '\t' << value[edges[i][0]] << "->" << value[edges[i][1]];}cout << endl;cout << "e:";for (int i = 0; i < edgeNum; ++i) {cout << '\t' << e[i];}cout << endl;cout << "l:";for (int i = 0; i < edgeNum; ++i) {cout << '\t' << l[i];}cout << endl;cout << "l-e:";for (int i = 0; i < edgeNum; ++i) {cout << '\t' << l[i] - e[i];}cout << "\n\n";cout << "关键路径为:";for (int i = 0; i < length; ++i) {cout << value[criticalPath[i]] << " ";}return 0;}
运行结果如下:
相关文章:

【图论】关键路径求法c++
代码结构如下图: 其中topologicalSort(float**, int, int*, bool*, int, int)用来递归求解拓扑排序,topologicalSort(float**, int*&, int, int, int)传参图的邻接矩阵mat与结点个数n,与一个引用变量数组topo,返回一个布尔值…...

基于51单片机电子钟万年历LCD1602显示
51单片机的电子钟万年历LCD1602显示 🔴 🔵51单片机的电子钟万年历LCD1602显示🔴 🔵主要功能:🔴 🔵讲解视频🔴 🔵仿真图:🔴 🔵程序&…...
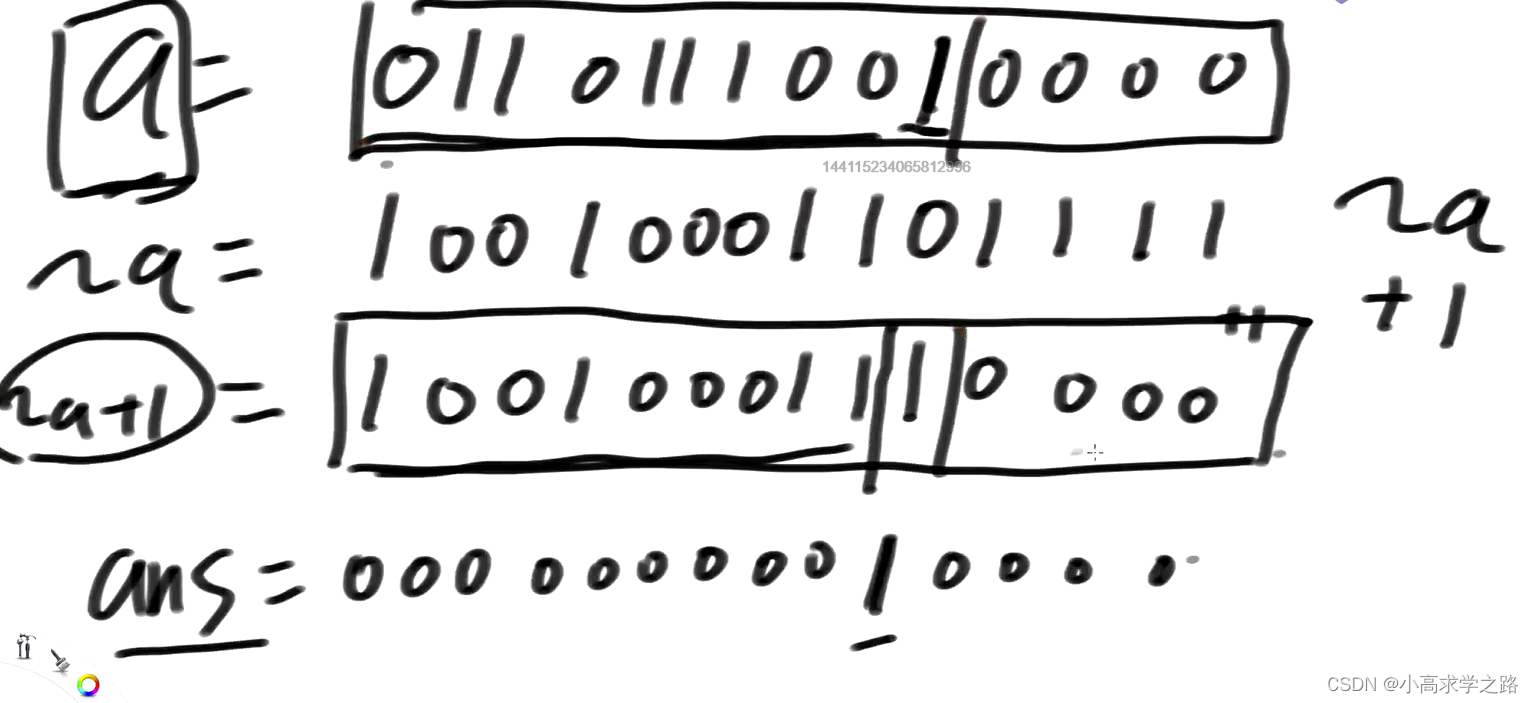
时间复杂度和运算
时间复杂度 在算法和数据结构中,有许多时间复杂度比 O(1) 更差的情况。以下是一些常见的时间复杂度,按照从最优到最差的顺序排列: O(1): 常数时间复杂度,操作的运行时间与输入规模无关,是最理想的情况。 O…...

深入Tailwind CSS中的文本样式
深入Tailwind CSS中的文本样式 样式文本是网页设计的一个基本组成部分,而 Tailwind CSS 提供了范围广泛的实用类,使文本样式设计既高效又有效。 在本本中,我们将探索文本样式的常见最佳实践,讨论潜在的陷阱,并推荐设计方法。我们…...
系统优化软件Bitsum Process Lasso Pro v12.4,供大家学习研究参考
1、自动或手动调整进程优先级;将不需要抑制的进程添加到排除列表; 2、设置动态提升前台运行的进程/线程的优先级 3、设置进程黑名单,禁止无用进程(机制为启动即结束,而非拦截其启动)。 4、优化I/O优先级以及电源模式自动化。 5、ProBalance功能。翻译成中文是“进程平衡…...

敏捷DevOps专家王立杰:端到端DevOps持续交付的5P法则 | IDCF
今天有一个流行的英文缩写词用来刻画这个风云变幻的时代:VUCA(乌卡时代)。四个英文字母分别表示动荡性(Volatility)、不确定性(Uncertainty)、复杂性(Complexity)和模糊性…...

分布式锁详解
文章目录 分布式锁1. [传统锁回顾](https://blog.csdn.net/qq_45525848/article/details/134608044?csdn_share_tail%7B%22type%22:%22blog%22,%22rType%22:%22article%22,%22rId%22:%22134608044%22,%22source%22:%22qq_45525848%22%7D)1.1. 从减库存聊起1.2. 环境准备1.3. 简…...
——算术运算符)
Python入门学习篇(二)——算术运算符
1 算术运算符 1.1 分类 类型含义示例注意事项加号12➡3“12”“3"➡"123”数值之间,是加法运算(True为1,False为0)字符串之间,是进行拼接数值和字符串之间是不可以使用加法运算的,会报错-减号1-2➡-1*乘号2*3➡6/除法2/1➡2.0除法的结果永远为小数%取余10%2➡0//取…...
微软发布最新.NET 8长期支持版本,云计算、AI应用支持再强化
11 月 15 日开始的为期三天的 .NET Conf 在线活动的开幕日上,.NET 8作为微软的开源跨平台开发平台正式发布。.NET 团队着重强调云、性能、全栈 Blazor、AI 和 .NET MAUI 是.NET 8的主要亮点。.NET团队在 .NET Conf 2023 [1]活动开幕式上表示:“通过这个版…...
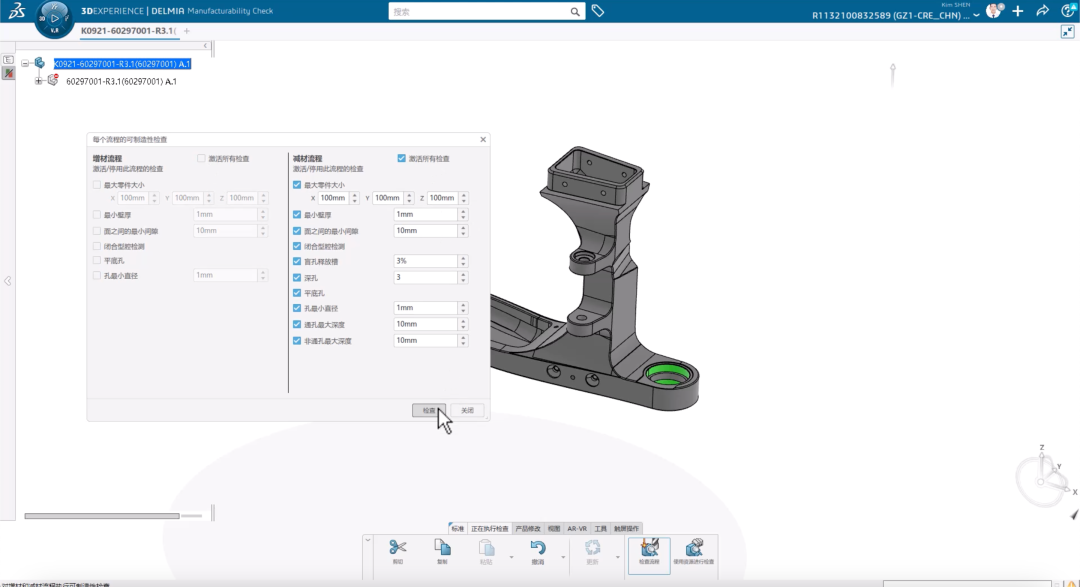
达索系统3DEXPERIENCE WORKS 2024 Fabrication新功能
当发现产品的制造环节,以及因产品模型本身的设计而导致制造环节存在不合理性,从而导致加工制造成本增加。 快速判断,轻松协作 在达索系统3DEXPERIENCE WORKS 2024中我们可以快速的判断产品的可制造性,以及快速与前端设计沟通协作…...

Web3与Web3.0: Web3指的是去中心化和基于区块链的网络,Web3.0指的是链接或语义网络。
目录 Web3与Web3.0: Web3指的是去中心化和基于区块链的网络 Web3.0指的是链接或语义网络。...

98、Text2Room: Extracting Textured 3D Meshes from 2D Text-to-Image Models
简介 github 利用预训练的2D文本到图像模型来合成来自不同姿势的一系列图像。为了将这些输出提升为一致的3D场景表示,将单目深度估计与文本条件下的绘画模型结合起来,提出了一个连续的对齐策略,迭代地融合场景帧与现有的几何形状࿰…...
)
MySQL 优化器 Index Condition Pushdown下推(ICP)
ICP 测试 准备数据 CREATE TABLE icp (employee_id int(6) NOT NULL AUTO_INCREMENT,first_name varchar(20) DEFAULT NULL,last_name varchar(25) DEFAULT NULL,email varchar(25) DEFAULT NULL,phone_number varchar(20) DEFAULT NULL,PRIMARY KEY (employee_id) );insert i…...
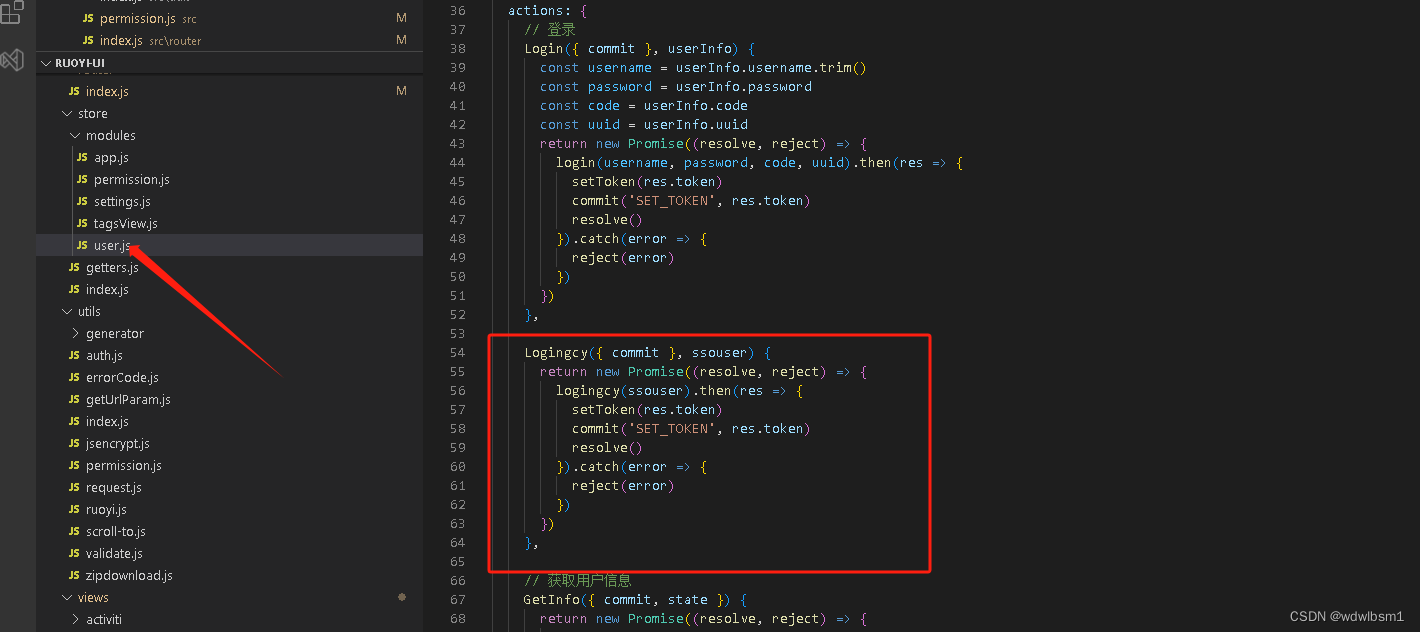
ruoyi 若依框架采用第三方登录
在项目中,前后端分离的若依项目,需要通过统一认证,或者是第三方协带认证信息跳转到本系统的指定页面。需要前后端都做相应的改造,由于第一次实现时已过了很久,再次重写时,发现还是搞了很长时间,…...

dom api
dom的全称为Document Object Model,即文档对象模型.所谓文档就是html页面,对象就是js里的对象,通过这个模型把页面上的元素和js里的对象关联起来. 下面是关于dom api的一些常用方法 1.获取元素 使用querySelector()方法获取一个元素 使用querySelectorAll()方法获取所有元素 当…...
)
音视频项目—基于FFmpeg和SDL的音视频播放器解析(二十一)
介绍 在本系列,我打算花大篇幅讲解我的 gitee 项目音视频播放器,在这个项目,您可以学到音视频解封装,解码,SDL渲染相关的知识。您对源代码感兴趣的话,请查看基于FFmpeg和SDL的音视频播放器 如果您不理解本…...

Qt项目打包发布超详细教程
https://blog.csdn.net/qq_45491628/article/details/129091320...

简单递归题
本来不想用递归做的,最后还是用了 题目如下: 洪尼玛有 n 块长度不同的木板,他想用这些木板拼成一个等边三角形的围栏,好将他的草泥马养在这个围栏里面。现在,给你这 n 块木板的长度,洪尼玛想知道他能否拼…...

再生式收音机踩坑记
下载《A Simple Regen Radio for Beginners》这篇文章也有好几年了,一直没有动手,上周末抽空做了一个,结果相当令人沮丧,一个台也收不到,用示波器测量三极管振荡波形,只有在调节再生电位器R2过程中…...

稻谷飘香金融助力——建行江门市分行助力乡村振兴
7月的台山,稻谷飘香。在大耕户李胜业的农田里,金灿灿的稻谷翻起层层稻浪,收割机在稻浪里来回穿梭,割稻、脱粒、装车等工序一气呵成。空气中弥漫着丰收的喜悦。 夏粮迎丰收的背后,是中国建设银行江门市分行(…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
