研习代码 day39 | 动态规划——完全背包的应用
一、爬楼梯(进阶版)
1.1 题目
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
输入描述
输入共一行,包含两个正整数,分别表示n, m
输出描述
输出一个整数,表示爬到楼顶的方法数。
输入示例
3 2输出示例
31.2 题目链接
57.爬楼梯
1.3 解题思路与过程想法
(1)解题思路
# 分析:这道题是 70.爬楼梯 的进阶版,对于每次爬楼的最多阶数是个不定值 n。是个典型的背包的排列问题。
排列问题:1+2+1 和 2+1+1 是两种不同方法
数组:爬到 i 阶,有 dp[i] 种方法
递推关系:求组成的方法数——————dp[j] += dp[j-i],
求背包装载的最大“价值” ——dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
求背包装载的最少“数量” ——dp[j] = min(dp[j], dp[j-weight[i]]+1)
初始化:求组成的方法数——dp[0] = 1
其他值初始化———初始化不影响覆盖的值,求最大-->初始化最小;
求最小-->初始化无穷大值
遍历顺序:因为是排列问题,所以先遍历背包容量,后遍历物体
此处 weight[i] 对应着 本次爬楼的阶数
value[i] 对应着 一次爬楼
(2)过程想法
比较经典,思路也比较好想,但需注意是排列问题
1.4 代码
def up(n,m) -> int:# 物品是每次爬的楼梯数,可重复---->完全背包# 背包容量 n,物品 1~m# 数组:爬到 i 阶,有 dp[i] 种方法dp = [0] * (n+1)# 递推关系:dp[j] += dp[j-i]# 初始化:求方法数,一般初始化 dp[0] = 1,若是0则后续将全是 0 dp[0] = 1for j in range(1,n+1): # 遍历背包for i in range(1,m+1): # 遍历物体if j >= i:dp[j] += dp[j-i]return dp[n]if __name__ == "__main__":# 从键盘端一次性连续读取两个数字inputs = input()# 将输入拆分为两个数字num1, num2 = map(int, inputs.split())print(up(num1,num2))二、零钱兑换
2.1 题目
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11输出:3解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 2^31 - 10 <= amount <= 10^4
2.2 题目链接
322.零钱兑换
2.3 解题思路与过程想法
(1)解题思路
# 数组:构成总金额 j 所需的最少硬币数 dp[j]
# 初始化:初始一个不会覆盖其他值的原始值(求最小,赋无穷大)
# 递推关系:dp[j] = min(dp[j],dp[j-coin]+1)
# 完全背包的组合问题:先遍历物体,后遍历背包容量
(2)过程想法
针对纯完全背包问题变化不是很大,代码比较好写
2.4 代码
class Solution:def coinChange(self, coins: List[int], amount: int) -> int:# 完全背包:组合问题# 数组:构成总金额 j 所需的最少硬币数 dp[j]# 初始化:初始一个不会覆盖其他值的原始值dp = [float('inf')] * (amount+1)# 递推关系:dp[j] = min(dp[j],dp[j-coin]+1)# 初始化 dp[0] = 0# 举例递推 for coin in coins: # 遍历物品for j in range(coin,amount+1): # 遍历背包dp[j] = min(dp[j],dp[j-coin]+1)return dp[amount] if dp[amount] != float('inf') else -1三、完全平方数
3.1 题目
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12 输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13 输出:2 解释:13 = 4 + 9
提示:
1 <= n <= 10^4
3.2 题目链接
279.完全平方数
3.3 解题思路与过程想法
(1)解题思路
分析:整个题目的变体主要在于“完全平方数”,为了便于遍历,以其需“平方”的数为遍历数。
# 数组:i 最少可由 dp[i] 个完全平方数组成
# 初始化:初始一个不会覆盖其他值的原始值(求最小,赋无穷大)
# 递推关系:dp[j] = min(dp[j],dp[j-i*i]+1)
# 完全背包的组合问题:先遍历物体,后遍历背包容量
(2)过程想法
分析出变化的关系,代码是很好写的
3.4 代码
class Solution:def numSquares(self, n: int) -> int:# 完全背包问题-组合问题# 数组:i 最少可由 dp[i] 个完全平方数组成dp = [float('inf')] * (n+1)# 递推关系:dp[j] = min(dp[j],dp[j-i*i]+1)# 初始化dp[0] = 0for i in range(n//2+1): # 遍历物体for j in range(i*i,n+1): # 遍历背包dp[j] = min(dp[j], dp[j - i*i]+1)# 处理边界情况return dp[n] if n != 1 else 1相关文章:

研习代码 day39 | 动态规划——完全背包的应用
一、爬楼梯(进阶版) 1.1 题目 题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬至多m (1 < m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意:给定 n 是一个正整数。 输入描述 输入共一…...
 - 流控制语句)
Rust语言入门教程(五) - 流控制语句
if 表达式 在Rust中, if语句的判断条件不需要用( )括起来, 它会认为所有在if 和 {之间的表达式就是判断条件,例如: if num 5 {msg "five"; }判断条件的表达式必须返回一个bool型的值, 因为Rust是一个不喜…...

字符串:leetcode1410. HTML 实体解析器
1410. HTML 实体解析器 「HTML 实体解析器」 是一种特殊的解析器,它将 HTML 代码作为输入,并用字符本身替换掉所有这些特殊的字符实体。 HTML 里这些特殊字符和它们对应的字符实体包括: 双引号:字符实体为 " ÿ…...
springboot+vue项目如何集成onlyoffice开源文档组件
一、onlyoffice是什么 ONLYOFFICE 是一个开源的办公套件,适合多人在线协作。由总部位于总部在拉脱维亚的 IT 公司Acensio System SIA 开发。它提供在线协作文档编辑器(包括文档、电子表格、演示文稿和表单),适用于 Windows、Linu…...

Android okhttp3.0配置https信任所有证书
参考: Android okhttp3.0配置https的自签证书和信任所有证书 private OkHttpClient getHttpsClient() {OkHttpClient.Builder okhttpClient new OkHttpClient().newBuilder();//信任所有服务器地址okhttpClient.hostnameVerifier(new HostnameVerifier() {Overridepublic boo…...
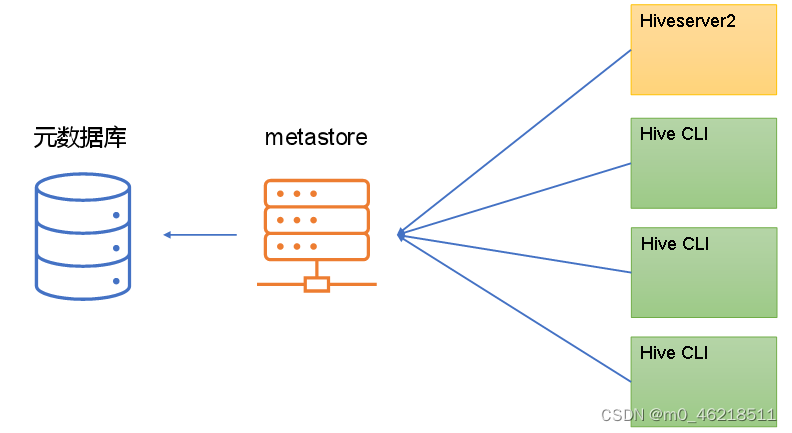
大数据基础设施搭建 - Hive
文章目录 一、上传压缩包二、解压压缩包三、配置环境变量四、初始化元数据库4.1 配置MySQL地址4.2 拷贝MySQL驱动4.3 初始化元数据库4.3.1 创建数据库4.3.2 初始化元数据库 五、启动元数据服务metastore5.1 修改配置文件5.2 启动/关闭metastore服务 六、启动hiveserver2服务6.1…...
手把手教你安装 Visual Studio 2022 及其简单使用
软件下载 打开 Visual Studio 官网,个人选择免费的Community社区版就够用了。 软件安装 双击运行安装程序: 点击继续 即可: 等待加载完成: 可以看到 Visual Studio 2022 对应不同的开发需求提供了若干工作负载,这里以…...

在MySQL中,修改字段A相同的记录的字段B ,要使得字段C小的记录的字段B值等于字段C大的记录的字段B值
例如:更新具有相同电话号码的用户记录,使得updatetime小的记录的name值等于updatetime大的记录的name值。 首先,我们需要创建一个用户表,这个用户表包含以下字段:phone,updatetime, name。以下是创建这个表…...

Java WebSocket 客户端接收大量数据
介绍 WebSocket 是一种基于 TCP 协议的全双工通信协议,它能够在客户端和服务器之间建立一个持久连接,实现实时的双向数据传输。在实际应用中,有时候我们需要处理大量的数据,例如实时监控系统或者实时股票行情等。本文将介绍如何使…...
)
QT 在Windows下实现ping功能(ICMP)
前言 很多时候,我们可能会图省事直接调用系统中的ping命令,但这是很不科学的~ 废话不多说,直接上代码.. .pro文件 在.pro文件末尾添加一行: LIBS -liphlpapi -lws2_32 .h文件 在.h文件中加入: #include <Q…...

harmonyos应用开发者高级认证考试部分答案
1只要使用端云一体化的云端资源就需要支付费用(错) 2所有使用Component修饰的自定义组件都支持onPageShow,onBackPress和onPageHide生命周期函数。(错) 3 HarmonyOS应用可以兼容OpenHarmony生态(对&#…...

基于 STM32Cube.AI 的嵌入式人脸识别算法实现
本文介绍了如何使用 STM32Cube.AI 工具开发嵌入式人脸识别算法。首先,我们将简要介绍 STM32Cube.AI 工具和 STM32F系列单片机的特点。接下来,我们将详细讨论如何使用 STM32Cube.AI 工具链和相关库来进行人脸识别算法的开发和优化。最后,我们提…...

ElasticSearch之cat allocation API
查看各节点上各个shard的硬件使用情况,命令样例如下: curl -X GET "https://localhost:9200/_cat/allocation?vtrue&pretty" --cacert $ES_HOME/config/certs/http_ca.crt -u "elastic:ohCxPHQBEs5*lo7F9"执行结果如下&#x…...
)
Vue + Element UI 实现复制当前行数据功能(复制到新增页面组件值不能更新等问题解决)
1、需求 使用Vue Element UI 实现在列表的操作栏新增一个复制按钮,复制当前行的数据可以打开新增弹窗后亦可以跳转到新增页面,本文实现为跳转到新增页面。 2、实现 1)列表页 index.vue <el-table> <!-- 其他列 --> <el-t…...
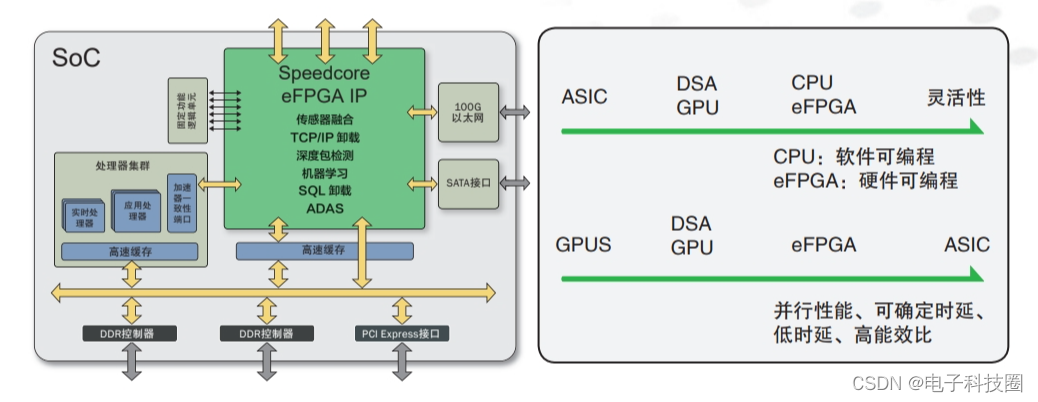
嵌入式FPGA IP正在发现更广阔的用武之地
作者:郭道正, Achronix Semiconductor中国区总经理 在日前落幕的“中国集成电路设计业2023年会暨广州集成电路产业创新发展高峰论坛(ICCAD 2023)”上,Achronix的Speedcore™嵌入式FPGA硅知识产权(eFPGA IP)…...

[点云分割] 条件欧氏聚类分割
介绍 条件欧氏聚类分割是一种基于欧氏距离和条件限制的点云分割方法。它通过计算点云中点与点之间的欧氏距离,并结合一定的条件限制来将点云分割成不同的区域或聚类。 在条件欧氏聚类分割中,通常会定义以下两个条件来判断两个点是否属于同一个聚类&…...

Spring事务粒度优化与传播机制
在Spring事务中,我们通常会为了控制事务粒度,会把它进行拆分,为了避免大事务执行太久,占用资源太多,导致资源利用率低的问题。 我们曾经就遇到老系统因为大事务,把服务打死了。 问题出在一个大事务中有一…...
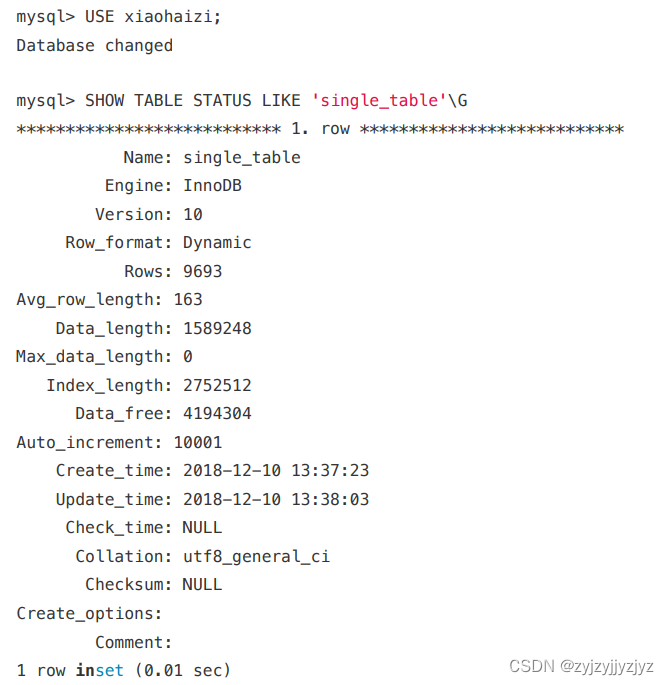
MySQL 基于成本的优化
其实在MySQL中⼀条查询语句的执⾏成本是由下边这两个⽅⾯组成的: I/O成本 我们的表经常使⽤的MyISAM、InnoDB存储引擎都是将数据和索引都存储到磁盘上的,当我们想查询表中的记录时,需要先把数据或者索引加载到内存中 然后再操作。这个从磁盘…...
【maven】【IDEA】idea中使用maven编译项目,报错java: 错误: 找不到符号 【2】
idea中使用maven编译项目,报错java: 错误: 找不到符号 错误状况展示: 如果报这种错,是因为项目中真的找不到报错的方法或者枚举 字段之类的,但实际是 : 点击 File Path...
AIGC,ChatGPT AI绘画 Midjourney 注册流程详细步骤
AI 绘画,Midjourney完成高清图片绘制,轻松掌握AI工具。 前期准备: ① 一个能使用的谷歌账号 ② 可以访问外网 Midjourney注册 1.进入midjourney官网https://www.midjourney.com 点击左下角”Join the Beta”,就可以注册,第一次使用的小伙伴会弹出提示,只需要点击Acc…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
