新手如何买卖可转债,可转债投资基础入门

一、教程描述
什么是可转债?可转债是可转换债券的二次简称,原始全称是可转换公司债券,这是一种可以在特定时间、按特定条件,转换为普通股票的特殊企业债券,可转换债券兼具债权和股权的特征,其英文为convertible bond(或者convertible debenture、convertible note)。本套教程资源,大小2.06G,共有12个文件。
二、教程目录
01.可转债第一课:神奇的可转债.mp4
02.可转债第二课:公司会不还钱么?.mp4
03.可转债第三课:如何赚取可转债的高收益.mp4
04.可转债第四课:转股价真的有这么简单么?.mp4
05.可转债第五课:在绝望中寻找希望-强制赎回.mp4
06.可转债第六课:番外篇之调转股价.mp4
07.可转债第七课:回售条款的秘密.mp4
08.可转债第八课:鸡蛋永远不要放在一个篮子里.mp4
09.可转债第九课:宁缺毋滥,分步建仓.mp4
10.可转债第十课:你真的会打新么?.mp4
11.可转债第十一课:带你从头到尾来实操.mp4
12.可转债第十二课:可转债你不知道的那些事.mp4
三、教程下载
百度一下“宝贝分享网”,站内搜索关键词获取。
相关文章:

新手如何买卖可转债,可转债投资基础入门
一、教程描述 什么是可转债?可转债是可转换债券的二次简称,原始全称是可转换公司债券,这是一种可以在特定时间、按特定条件,转换为普通股票的特殊企业债券,可转换债券兼具债权和股权的特征,其英文为conver…...

研习代码 day39 | 动态规划——完全背包的应用
一、爬楼梯(进阶版) 1.1 题目 题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬至多m (1 < m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意:给定 n 是一个正整数。 输入描述 输入共一…...
 - 流控制语句)
Rust语言入门教程(五) - 流控制语句
if 表达式 在Rust中, if语句的判断条件不需要用( )括起来, 它会认为所有在if 和 {之间的表达式就是判断条件,例如: if num 5 {msg "five"; }判断条件的表达式必须返回一个bool型的值, 因为Rust是一个不喜…...

字符串:leetcode1410. HTML 实体解析器
1410. HTML 实体解析器 「HTML 实体解析器」 是一种特殊的解析器,它将 HTML 代码作为输入,并用字符本身替换掉所有这些特殊的字符实体。 HTML 里这些特殊字符和它们对应的字符实体包括: 双引号:字符实体为 " ÿ…...
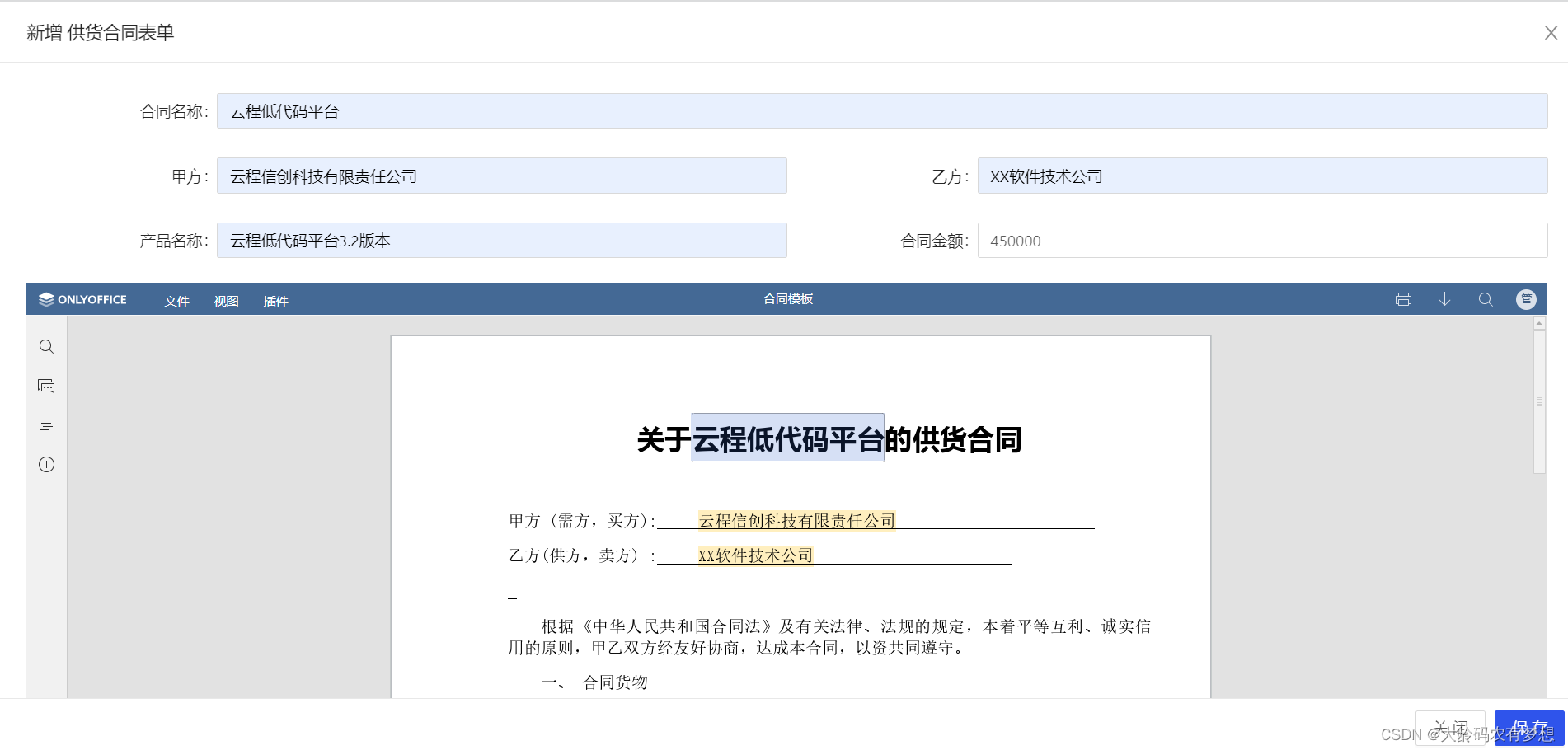
springboot+vue项目如何集成onlyoffice开源文档组件
一、onlyoffice是什么 ONLYOFFICE 是一个开源的办公套件,适合多人在线协作。由总部位于总部在拉脱维亚的 IT 公司Acensio System SIA 开发。它提供在线协作文档编辑器(包括文档、电子表格、演示文稿和表单),适用于 Windows、Linu…...

Android okhttp3.0配置https信任所有证书
参考: Android okhttp3.0配置https的自签证书和信任所有证书 private OkHttpClient getHttpsClient() {OkHttpClient.Builder okhttpClient new OkHttpClient().newBuilder();//信任所有服务器地址okhttpClient.hostnameVerifier(new HostnameVerifier() {Overridepublic boo…...
大数据基础设施搭建 - Hive
文章目录 一、上传压缩包二、解压压缩包三、配置环境变量四、初始化元数据库4.1 配置MySQL地址4.2 拷贝MySQL驱动4.3 初始化元数据库4.3.1 创建数据库4.3.2 初始化元数据库 五、启动元数据服务metastore5.1 修改配置文件5.2 启动/关闭metastore服务 六、启动hiveserver2服务6.1…...
手把手教你安装 Visual Studio 2022 及其简单使用
软件下载 打开 Visual Studio 官网,个人选择免费的Community社区版就够用了。 软件安装 双击运行安装程序: 点击继续 即可: 等待加载完成: 可以看到 Visual Studio 2022 对应不同的开发需求提供了若干工作负载,这里以…...

在MySQL中,修改字段A相同的记录的字段B ,要使得字段C小的记录的字段B值等于字段C大的记录的字段B值
例如:更新具有相同电话号码的用户记录,使得updatetime小的记录的name值等于updatetime大的记录的name值。 首先,我们需要创建一个用户表,这个用户表包含以下字段:phone,updatetime, name。以下是创建这个表…...

Java WebSocket 客户端接收大量数据
介绍 WebSocket 是一种基于 TCP 协议的全双工通信协议,它能够在客户端和服务器之间建立一个持久连接,实现实时的双向数据传输。在实际应用中,有时候我们需要处理大量的数据,例如实时监控系统或者实时股票行情等。本文将介绍如何使…...
)
QT 在Windows下实现ping功能(ICMP)
前言 很多时候,我们可能会图省事直接调用系统中的ping命令,但这是很不科学的~ 废话不多说,直接上代码.. .pro文件 在.pro文件末尾添加一行: LIBS -liphlpapi -lws2_32 .h文件 在.h文件中加入: #include <Q…...

harmonyos应用开发者高级认证考试部分答案
1只要使用端云一体化的云端资源就需要支付费用(错) 2所有使用Component修饰的自定义组件都支持onPageShow,onBackPress和onPageHide生命周期函数。(错) 3 HarmonyOS应用可以兼容OpenHarmony生态(对&#…...

基于 STM32Cube.AI 的嵌入式人脸识别算法实现
本文介绍了如何使用 STM32Cube.AI 工具开发嵌入式人脸识别算法。首先,我们将简要介绍 STM32Cube.AI 工具和 STM32F系列单片机的特点。接下来,我们将详细讨论如何使用 STM32Cube.AI 工具链和相关库来进行人脸识别算法的开发和优化。最后,我们提…...

ElasticSearch之cat allocation API
查看各节点上各个shard的硬件使用情况,命令样例如下: curl -X GET "https://localhost:9200/_cat/allocation?vtrue&pretty" --cacert $ES_HOME/config/certs/http_ca.crt -u "elastic:ohCxPHQBEs5*lo7F9"执行结果如下&#x…...
)
Vue + Element UI 实现复制当前行数据功能(复制到新增页面组件值不能更新等问题解决)
1、需求 使用Vue Element UI 实现在列表的操作栏新增一个复制按钮,复制当前行的数据可以打开新增弹窗后亦可以跳转到新增页面,本文实现为跳转到新增页面。 2、实现 1)列表页 index.vue <el-table> <!-- 其他列 --> <el-t…...
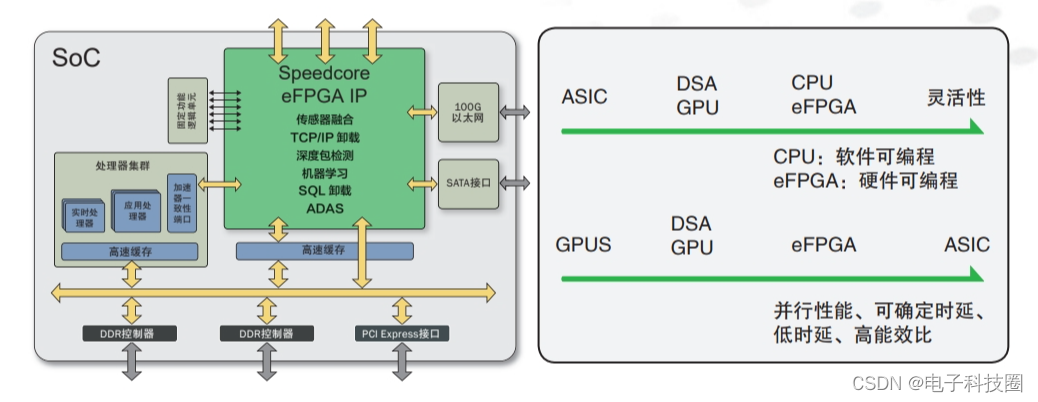
嵌入式FPGA IP正在发现更广阔的用武之地
作者:郭道正, Achronix Semiconductor中国区总经理 在日前落幕的“中国集成电路设计业2023年会暨广州集成电路产业创新发展高峰论坛(ICCAD 2023)”上,Achronix的Speedcore™嵌入式FPGA硅知识产权(eFPGA IP)…...

[点云分割] 条件欧氏聚类分割
介绍 条件欧氏聚类分割是一种基于欧氏距离和条件限制的点云分割方法。它通过计算点云中点与点之间的欧氏距离,并结合一定的条件限制来将点云分割成不同的区域或聚类。 在条件欧氏聚类分割中,通常会定义以下两个条件来判断两个点是否属于同一个聚类&…...

Spring事务粒度优化与传播机制
在Spring事务中,我们通常会为了控制事务粒度,会把它进行拆分,为了避免大事务执行太久,占用资源太多,导致资源利用率低的问题。 我们曾经就遇到老系统因为大事务,把服务打死了。 问题出在一个大事务中有一…...
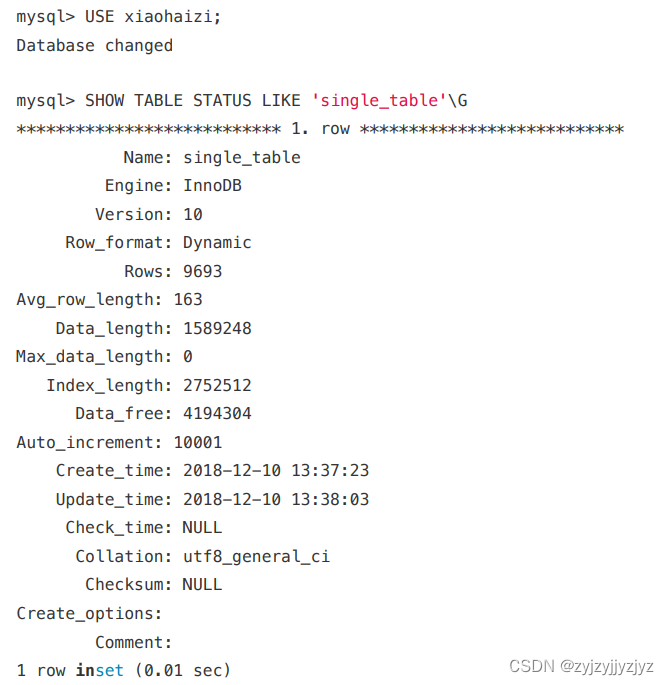
MySQL 基于成本的优化
其实在MySQL中⼀条查询语句的执⾏成本是由下边这两个⽅⾯组成的: I/O成本 我们的表经常使⽤的MyISAM、InnoDB存储引擎都是将数据和索引都存储到磁盘上的,当我们想查询表中的记录时,需要先把数据或者索引加载到内存中 然后再操作。这个从磁盘…...
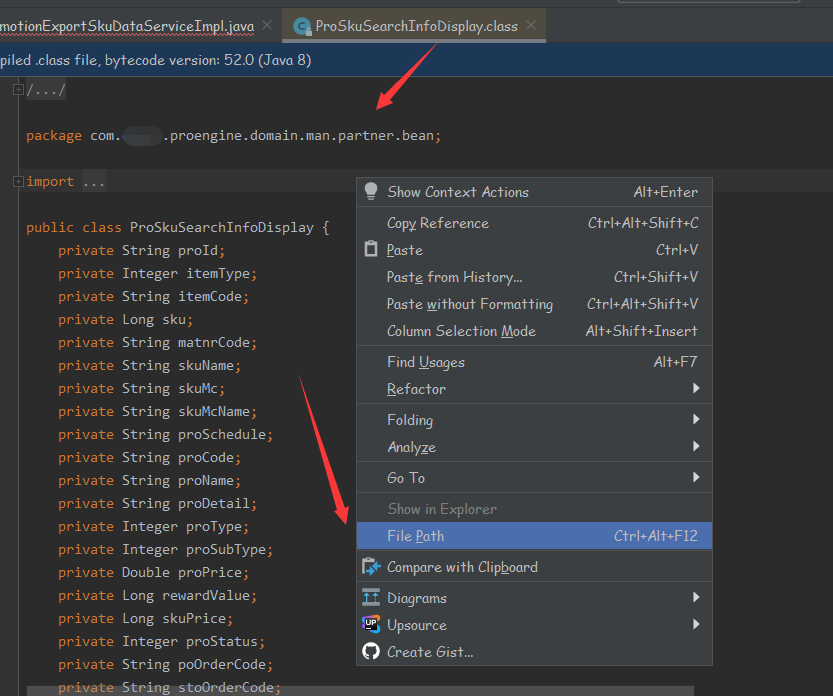
【maven】【IDEA】idea中使用maven编译项目,报错java: 错误: 找不到符号 【2】
idea中使用maven编译项目,报错java: 错误: 找不到符号 错误状况展示: 如果报这种错,是因为项目中真的找不到报错的方法或者枚举 字段之类的,但实际是 : 点击 File Path...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
