日志技术logback
一,日志概括

二,日志技术的特点

三,日志技术的体系


三,入门

四,案例
package XinZheng;import org.slf4j.Logger;
import org.slf4j.LoggerFactory;public class Main58 {//1,创建一个Logger日志对象public static final Logger LOGGER= LoggerFactory.getLogger("Main58");public static void main(String[] args) {try {LOGGER.info("chu方法开始执行");chu(10,20);LOGGER.info("chu方法执行成功");} catch (Exception e) {LOGGER.info("chu方法执行失败");}}public static void chu(int a,int b){LOGGER.info("参数a"+a);LOGGER.info("参数b"+b);int c =a/b;System.out.println("结果是"+c);}
}
五,logbeack .xml(核心配置文件)



六,日志级别
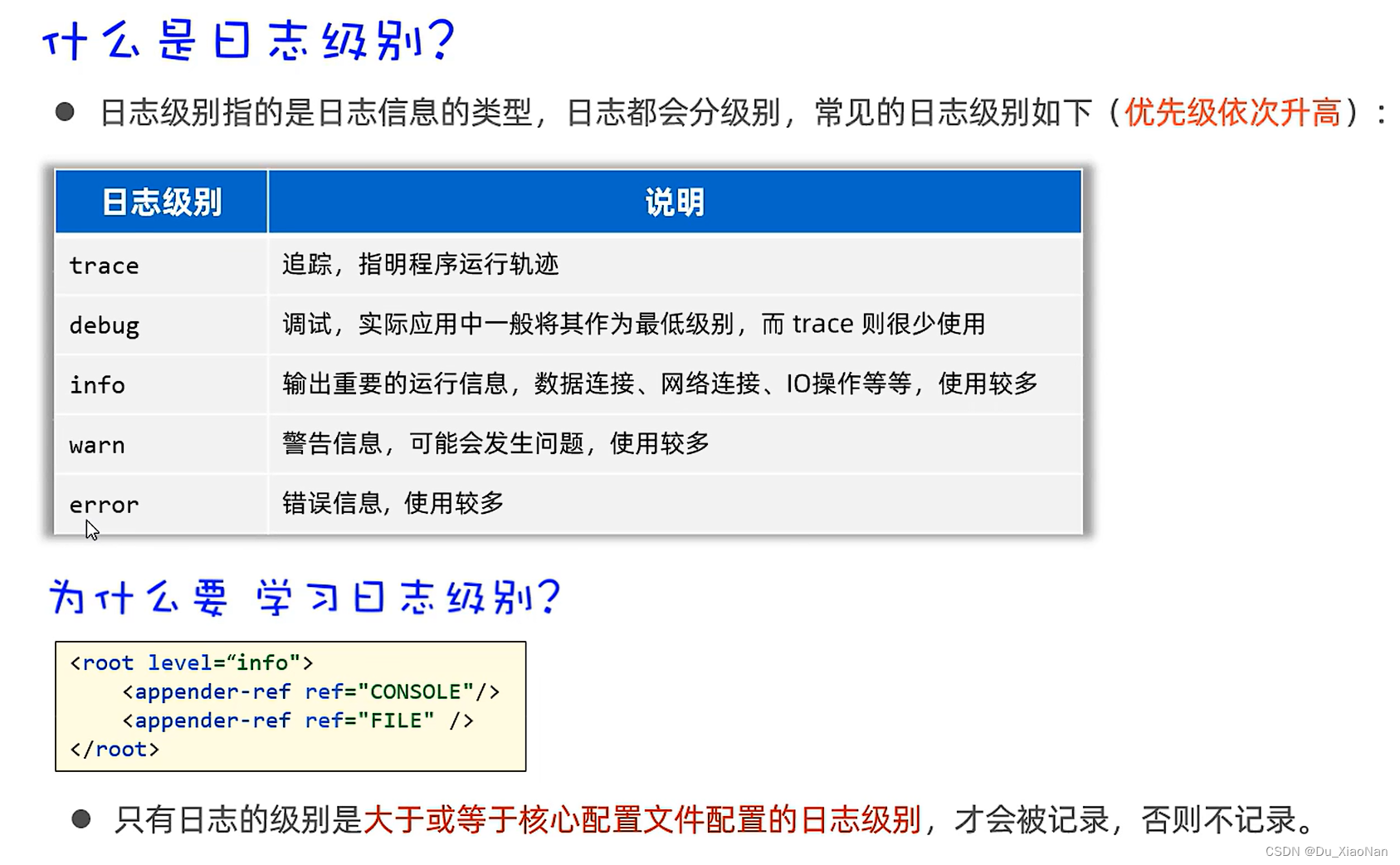
相关文章:

日志技术logback
一,日志概括 二,日志技术的特点 三,日志技术的体系 三,入门 四,案例 package XinZheng;import org.slf4j.Logger; import org.slf4j.LoggerFactory;public class Main58 {//1,创建一个Logger日志对象public static fi…...
之build构建系统基础(一))
linux(1)之build构建系统基础(一)
Linux(1)之buildroot构建系统(一) Author:Onceday Date:2023年11月12日 漫漫长路,才刚刚开始… 参考文档: The Yocto ProjectBuildroot - Making Embedded Linux Easy 文章目录 Linux(1)之buildroot构建系统(一)1. 概述1.1 如…...
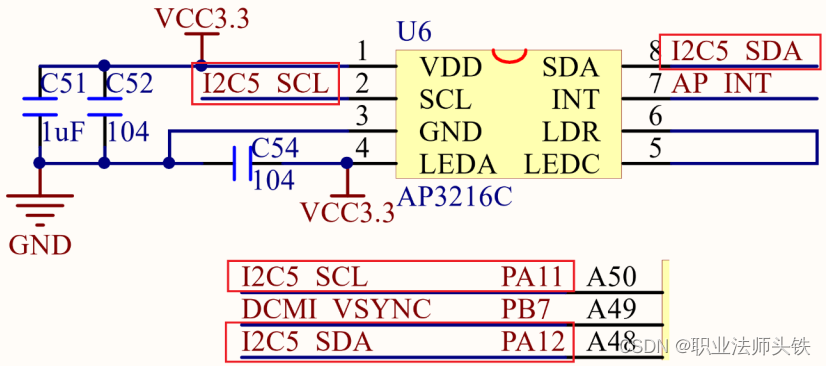
25 Linux I2C 驱动
一、I2C简介 I2C老朋友了,在单片机里面也学过,现在再复习一下。I2C使用两条线在主控制器和从机之间进行数据通信。一条是 SCL(串行时钟线),另外一条是 SDA(串行数据线),这两条数据线需要接上拉电阻,总线空闲的时候 SCL…...

API 设计:使用 Node.js 和 Express.js 的综合教程
API(应用程序编程接口)设计涉及创建一个高效而强大的接口,允许不同的软件应用程序相互交互。 说明 本教程将指导您使用 Node.js 和 Express.js 作为核心技术来规划、设计和构建 API。但是,这些原则可以应用于任何语言或框架。我们…...

vite和webpack的区别和练习
Vite和Webpack都是现代化的前端构建工具,但它们之间存在一些区别: 构建性能:Vite使用ES Modules提高了构建性能,可以在构建时只构建需要的部分,而Webpack则需要在构建时处理整个应用程序。 开发体验:Vite具…...

Python与设计模式--装饰器模式
6-Python与设计模式–装饰器模式 一、快餐点餐系统 又提到了那个快餐点餐系统,不过今天我们只以其中的一个类作为主角:饮料类。 首先,回忆下饮料类: class Beverage():name ""price 0.0type "BEVERAGE"…...
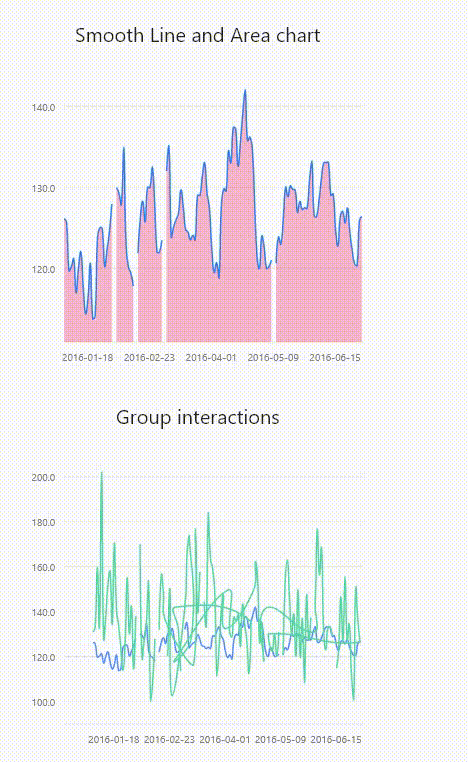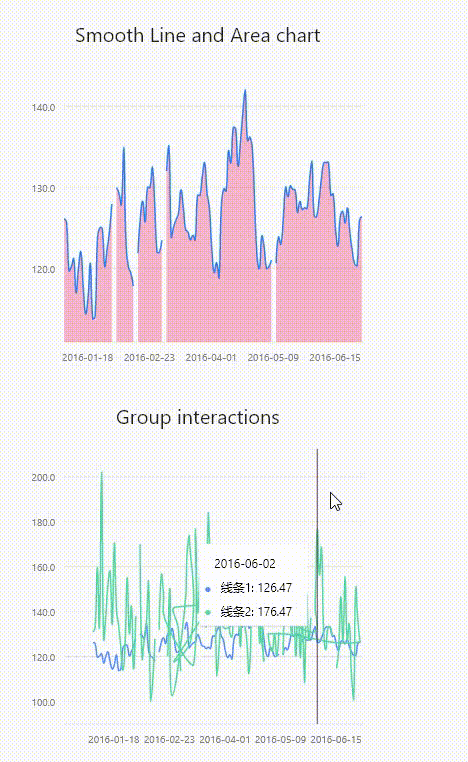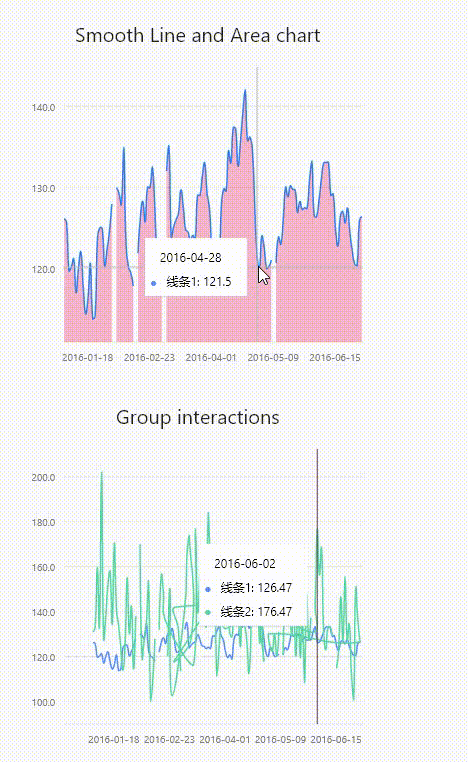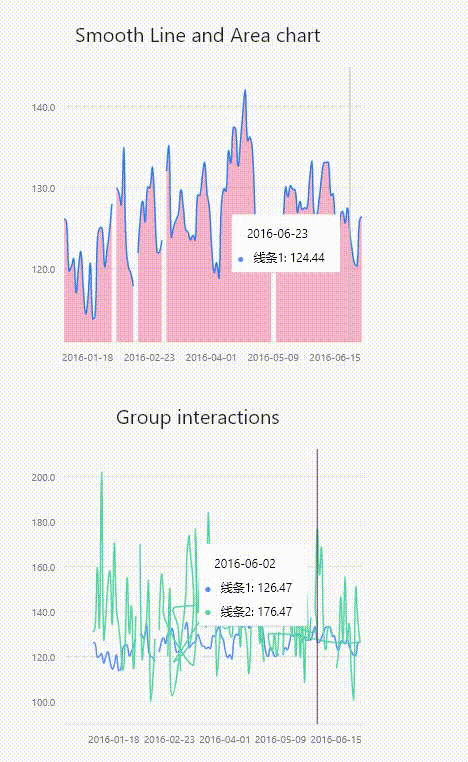
flutter之graphic图表自定义tooltip
renderer graphic中tooltip的TooltipGuide类提供了renderer方法,接收三个参数Size类型,Offset类型,Map<int, Tuple>类型。可查到的文档是真的少,所以只能在源码中扒拉例子,做符合需求的修改。 官方github示例 …...

逆向扒cocosjs安卓包教程-破解加密的js源码
本文只适用于cocosjs引擎打包的游戏apk,针对此类apk进行源码级别的逆向破解,可直接逐个破解工程内的源码部分,让游戏逻辑大白于你的面前,你可以针对js源码进行二次开发。按照我的教程破解过程中遇到什么问题,欢迎留言。 目录 准备apk包 查找加密key 解密jsc文件 方案1…...

Kafka(一)
一:简介 解决高吞吐量项目的需求 是一款为大数据而生的消息中间件,具有百亿级tps的吞吐量,在数据采集、传输、存储的过程中发挥着作用 二:为什么要使用消息队列 一个普通访问量的接口和一个大并发的接口,它们背后的…...
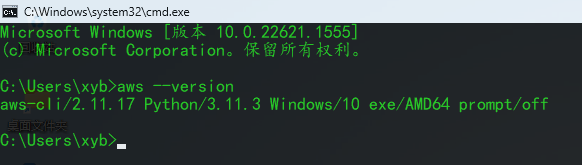
【Amazon】安装卸载AWS CLI操作流程(Windows 、Linux系统)
AWS 命令行界面(AWS CLI)是用于管理 AWS 产品的统一工具。只需要下载和配置一个工具,您就可以使用命令行控制多个 AWS 产品并利用脚本来自动执行这些服务。 AWS CLI v2 提供了多项新功能,包括改进的安装程序、新的配置选项&#…...

Django同时连接多种数据库
我的使用场景需要同时连接达梦数据库和MYSQL数据库,有的功能需要查询达梦,有的功能则需要查询MYSQL。 第一步:在 Django 的 settings.py 文件中,配置多个数据库连接。你可以在 DATABASES 字典中添加多个数据库配置。每个数据库配置…...
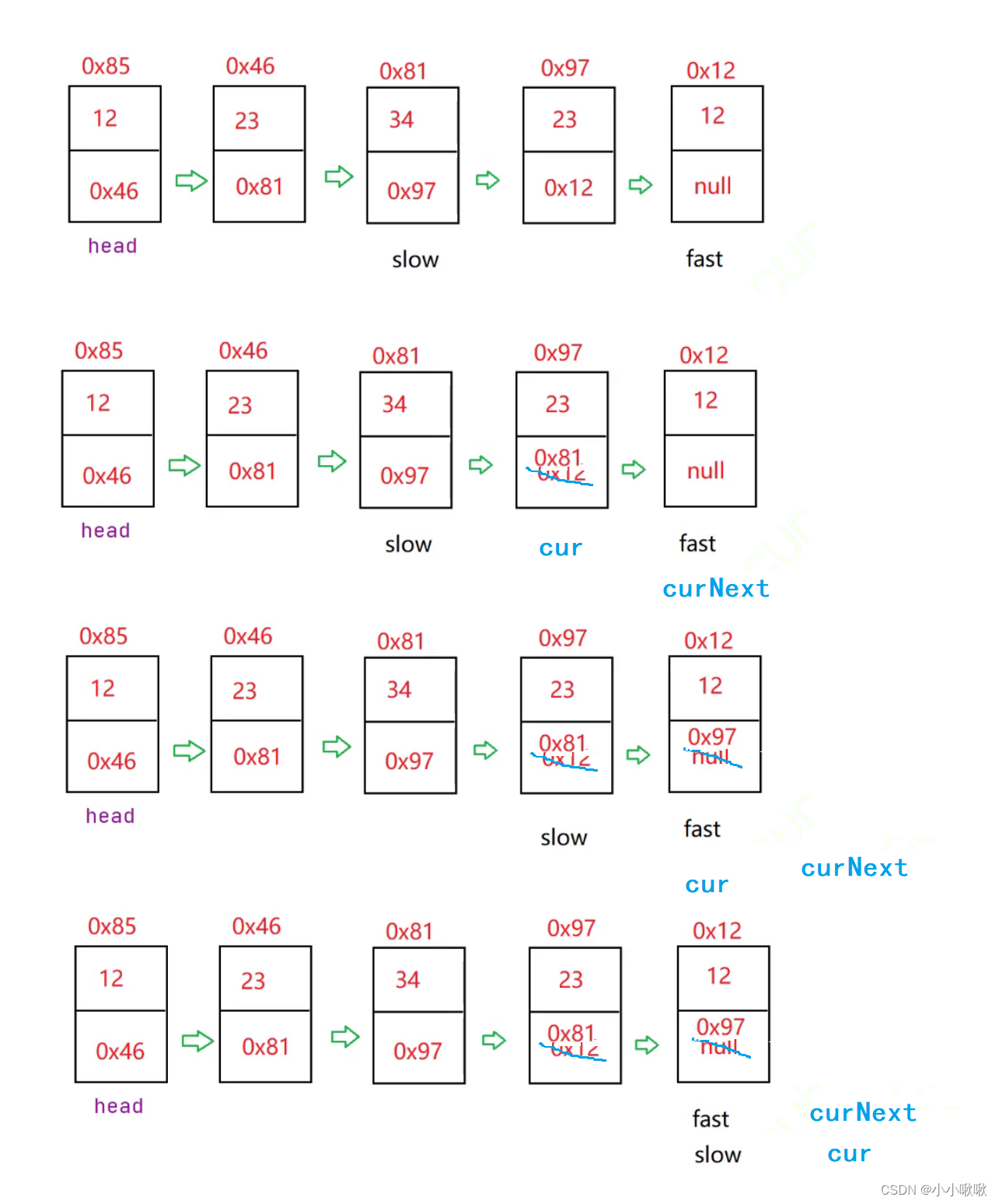
【链表之练习题】
文章目录 翻转链表找到链表的中间节点返回倒数第k个节点合并两个有序链表判断链表是否回文注意 翻转链表 //反转链表//实质上是把每一个节点头插法,原本第一个节点变成最后一个节点public ListNode reverseList(){//链表为空if (head null){return null;}//链表只有一个节点if…...

情感对话机器人的任务体系
人类在处理对话中的情感时,需要先根据对话场景中的蛛丝马迹判断出对方的情感,继而根据对话的主题等信息思考自身用什么情感进行回复,最后结合推理出的情感形成恰当的回复。受人类处理情感对话的启发,情感对话机器人需要完成以下几…...
)
【笔记 Pytorch 08】深度学习模板 (未完)
文章目录 一、声明二、工程结构三、文件内容main.pymodel.pydataset.pyutils.py 四、问题汇总 一、声明 非常感谢这些资料的作者: 【参考1】、【PyTorch速成教程 (by Sung Kim)】 二、工程结构 ├── main.py:实现训练 (train) 、验证(validation)和…...

【如何学习Python自动化测试】—— Cookie 处理
前提 网络通信是当今社会最为普及和繁荣的技术之一,其承载了人们生活中瞬息万变的信息传递和交流。而作为网络通信的核心要素,网络协议、socket、cookie和session则是网络通信的灵魂。 一、网络协议 网络协议是计算机和网络设备之间相互通信的规则和标准…...
IOS+Appium+Python自动化全实战教程
由于公司的产品坐落于不同的平台,如ios、mac、Android、windows、web。因此每次有新需求的时候,开发结束后,留给测试的时间也不多。此外,一些新的功能实现,偶尔会影响其他的模块功能正常的使用。 网上的ios自动化方面的…...
华硕灵耀XPro(UX7602ZM)原装Win11系统恢复安装教程方法
华硕灵耀XPro(UX7602ZM)原装Win11系统恢复安装教程方法: 第一步:需要自备华硕6个底包工厂安装包(EDN.KIT.OFS.SWP.HDI.TLK)或者自己备份的iso/esd/wim等镜像恢复 支持系列: 灵耀系列原装系统 无畏系列原装系统 枪…...
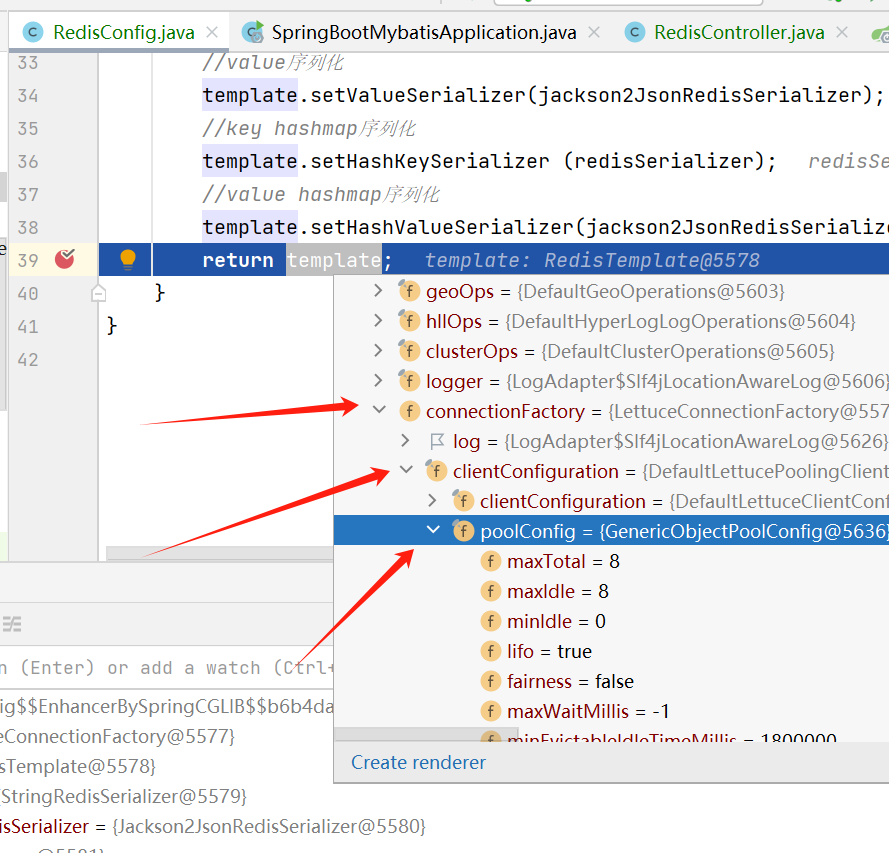
SpringBoot整合Redis,redis连接池和RedisTemplate序列化
SpringBoot整合Redis 1、SpringBoot整合redis1.1 pom.xml1.2 application.yml1.3 配置类RedisConfig,实现RedisTemplate序列化1.4 代码测试 2、SpringBoot整合redis几个疑问?2.1、Redis 连接池讲解2.2、RedisTemplate和StringRedisTemplate 3、RedisTemp…...

学习课题:逐步构建开发播放器【QT5 + FFmpeg6 + SDL2】
目录 一、播放器开发(一):播放器组成大致结构与代码流程设计 二、播放器开发(二):了解FFmpeg与SDL常用对象和函数 三、播放器开发(三):FFmpeg与SDL环境配置 四、播放器开发(四):多线程解复用与解码模块实现 五、播放器开发(五…...

Linux 6.7全面改进x86 CPU微码加载方式
导读最近,社区在清理 Linux 上的 Intel/AMD x86 CPU 微代码加载方面做了大量的工作,这些工作现已合并到 Linux 6.7 中。 由于在启动时加载 CPU 微代码对于减少不断出现的新 CPU 安全漏洞以及有时解决功能问题非常重要,Thomas Gleixner 最近开…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
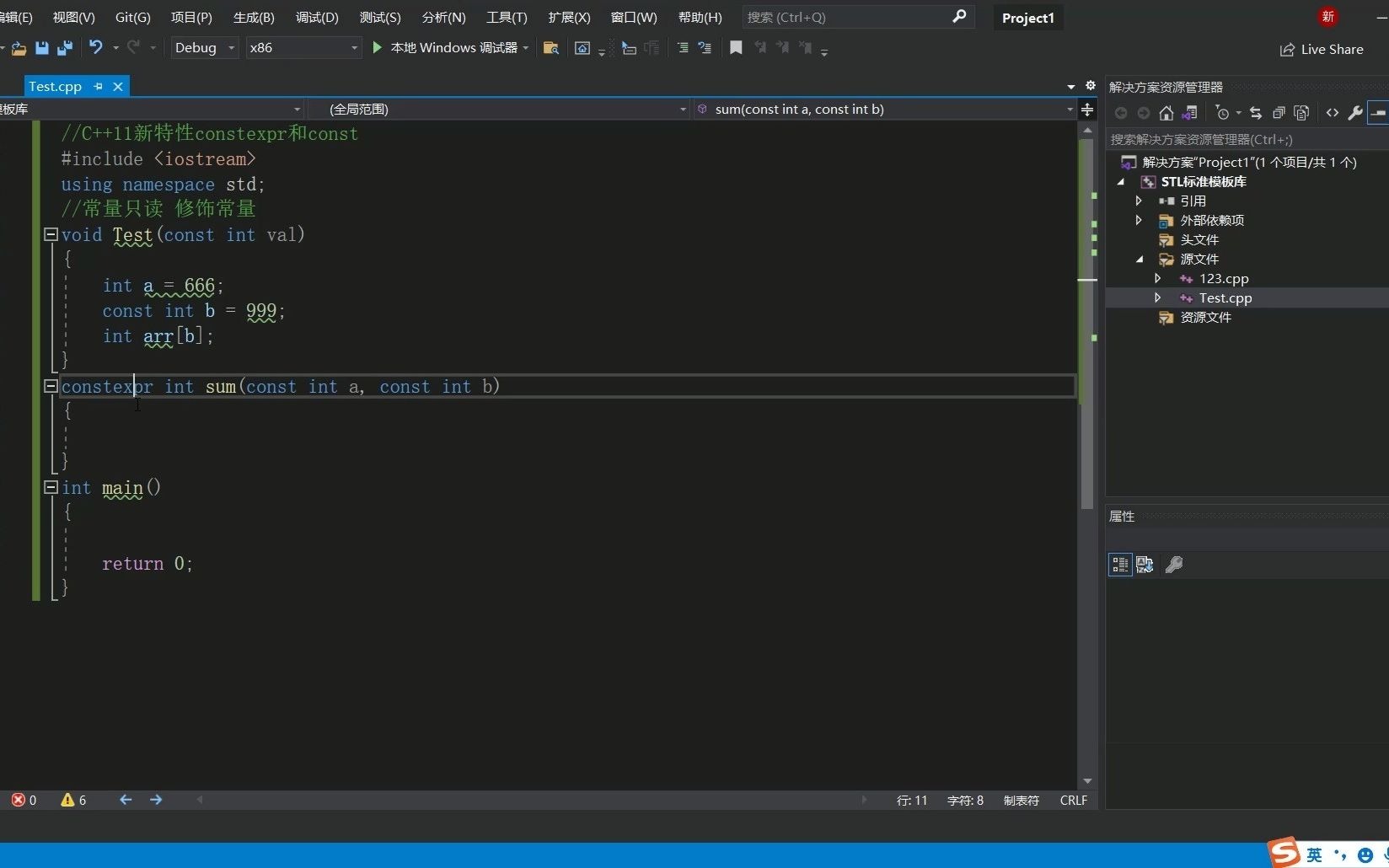
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...
