Linux(Centos)上使用crontab实现定时任务(定时执行脚本)
场景
Windows中通过bat定时执行命令和mysqldump实现数据库备份:
Windows中通过bat定时执行命令和mysqldump实现数据库备份_mysqldump bat-CSDN博客
上面讲windows中使用bat实现定时任务的方式,如果是在linux上可以通过crontab实现。
cron是服务名称。 crond是后台进程,用来执行脚本,在系统中一直会运行。
crontab是一个工具,用来管理定时任务列表,定制好的计划任务,需要启动crond服务(系统默认安装),
crond服务是通过crontab命令实现。
注:
博客:
霸道流氓气质_C#,架构之路,SpringBoot-CSDN博客
实现
1、首先新建一个sh脚本,用来清理指定文件夹下面的文件内容。
在var/test目录下新建clean.sh
touch clean.sh并修改内容如下
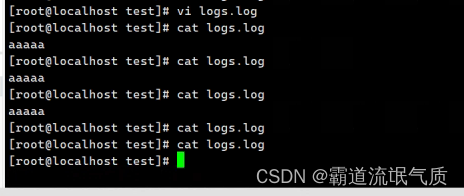
#!/bin/bashcd /var/test>logs.logexit此脚本会清理test目录下logs.log文件的内容。

新建logs.log文件并随便添加内容。
2、然后添加定时任务
设置定时任务,进入编辑模式,和vim操作一样
crontab -e将内容修改如下
* * * * * /var/test/clean.sh
前面跟的是cron表达式,这里代表一分钟执行一次。后面跟的是执行的命令
其它crontab执行表达式可以参考
crontab执行时间计算 - 在线工具
3、保存并退出后,可以在logs.log中添加内容,并一分钟后验证效果
4、如果要查看日志可以
tail -f /var/log/cron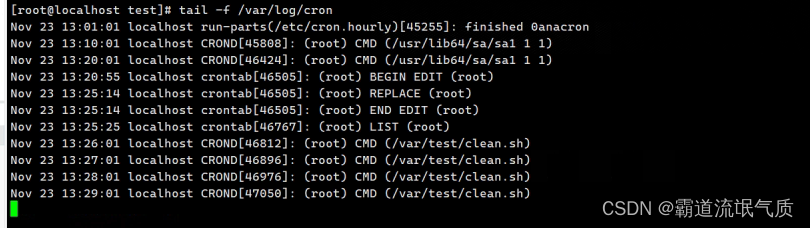
相关文章:

Linux(Centos)上使用crontab实现定时任务(定时执行脚本)
场景 Windows中通过bat定时执行命令和mysqldump实现数据库备份: Windows中通过bat定时执行命令和mysqldump实现数据库备份_mysqldump bat-CSDN博客 上面讲windows中使用bat实现定时任务的方式,如果是在linux上可以通过crontab实现。 cron是服务名称。…...

【Leetcode合集】20. 有效的括号
20. 有效的括号 20. 有效的括号 代码仓库地址: https://github.com/slience-me/Leetcode 个人博客 :https://slienceme.xyz 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串…...
)
OpenGL 绘制线(Qt)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 这里同样对OpenGL中的绘制线操作进行封装,便于后续的操作,很多形状也都是基于线来生成的,如圆形等。 二、实现代码 LineDrawable.h #ifndef LINE_DRAWABLE_H #define LINE_DRAWABLE_H#include...

Java | 多线程并发编程CountDownLatch实践
关注:CodingTechWork 引言 在一次数据割接需求中,数据需要通过编程的方式进行转移割接到新平台,此时若串行化方式,无疑会拉锯此次战斗,所以首当其冲要使用并发编程来降低割接时长。 本次主要考虑使用CountDownLatc…...

分布式定时任务系列6:XXL-job触发日志过大引发的CPU告警
传送门 分布式定时任务系列1:XXL-job安装 分布式定时任务系列2:XXL-job使用 分布式定时任务系列3:任务执行引擎设计 分布式定时任务系列4:任务执行引擎设计续 分布式定时任务系列5:XXL-job中blockingQueue的应用 …...

Spark RDD、DataFrame和Dataset的区别和联系
一、三种数据介绍 是Spark中的三种不同的数据结构,它们都可以用于分布式数据处理,但是它们的实现方式和使用方法略有不同。 RDD(弹性分布式数据集) RDD是Spark最初的核心数据结构,它是一个分布式的、只读的、可容错的…...
代码随想录算法训练营第四十五天|139.单词拆分、背包问题总结
LeetCode 139. 单词拆分 题目链接:139. 单词拆分 - 力扣(LeetCode) 这道题使用完全背包来实现,我们首先考虑字符串是否可以由字符串列表组成,因此dp数组大小为n 1 ,其意义是,在n个位置时是否能…...

深度学习卫星遥感图像检测与识别 -opencv python 目标检测 计算机竞赛
文章目录 0 前言1 课题背景2 实现效果3 Yolov5算法4 数据处理和训练5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **深度学习卫星遥感图像检测与识别 ** 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐…...

wxWidgets 3.2.4发布 —— 发布于2023年11月11日
稳定的3.2系列中的另一个版本现在可以在GitHub上获得。您可以在那里找到包含库源代码和文档的归档文件,以及所选Windows编译器(如Microsoft Visual C、MinGW-w64和TDM-GCC)的二进制文件。您还可以阅读此版本的更新文档,特别是&…...
PyQt6运行QTDesigner生成的ui文件程序
2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~共计18条视频,包括:2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~、第2讲 PyQt6库和工具库Q…...

基于mediapipe的人手21点姿态检测模型—CPU上检测速度惊人
前期的文章,我们介绍了MediaPipe对象检测与对象分类任务,也分享了MediaPipe的人手手势识别。在进行人手手势识别前,MediaPipe首先需要进行人手的检测与人手坐标点的检测,经过以上的检测后,才能把人手的坐标点与手势结合起来,进行相关的手势识别。 MediaPipe人手坐标点检测…...

系统架构设计: 21 论敏捷软件开发方法及其应用
论敏捷软件开发方法及其应用 请围绕“敏捷软件开发方法及其应用”论题,依次从以下三个方面进行论述。 ①简述你所参与开发的运用了敏捷技术的项目,以及你所担任的工作; ②分析并讨论敏捷<...

【深度学习】脸部修复,CodeFormer,论文,实战
代码: https://github.com/sczhou/CodeFormer https://huggingface.co/spaces/sczhou/CodeFormer 论文:https://arxiv.org/abs/2206.11253 Towards Robust Blind Face Restoration with Codebook Lookup Transformer 文章目录 论文摘要1 引言2 相关工…...

OpenGL_Learn14(光照贴图)
1. 漫反射贴图 在光照场景中,它通常叫做一个漫反射贴图(Diffuse Map)(3D艺术家通常都这么叫它),它是一个表现了物体所有的漫反射颜色的纹理图像。 我们会将纹理储存为Material结构体中的一个sampler2D 。我们将之前定义的vec3漫反…...
【JVM精讲与GC调优教程(概述)】
如何理解虚拟机(JVM)跨语言的平台 java虚拟机根本不关心运行在其内部的程序到底是使用何种编程语言编写的,他只关心“字节码”文件。 java不是最强大的语言,但是JVN是最强大的虚拟机。 不存在内存溢出? 内存泄露? JAVA = (C++)–; 垃圾回收机制为我们打理了很多繁琐的…...

蓝桥杯物联网竞赛_STM32L071_2_继电器控制
Stm32l071原理图: PA11与PA12连接着UNL2803 ULN2803是一种集成电路芯片,通常被用作高电压和高电流负载的驱动器。 ULN2803是一个达林顿阵列,当输入引脚(IN1至IN8)被连接到正电源时,相应的输出引脚ÿ…...
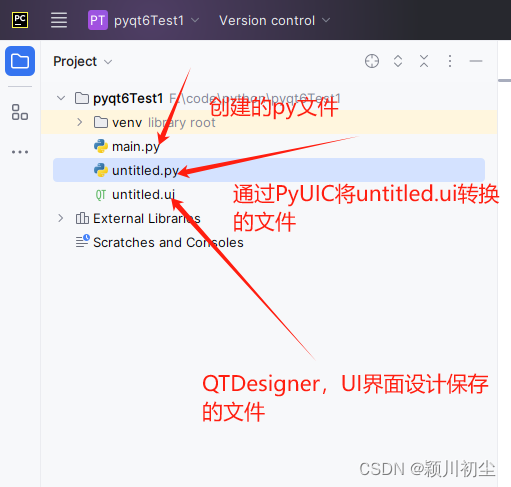
python之pyqt专栏2-项目文件解析
项目结构 在上一篇文章python之pyqt专栏1-环境搭建,创建新的pyqt项目,下面我们来看一下这个项目下的文件。 从下面的文件结构图可以看到,该项目下有3个文件,untitled.ui,untitled.py 以及main.py。 QtDesigner可以UI界面的方式&am…...
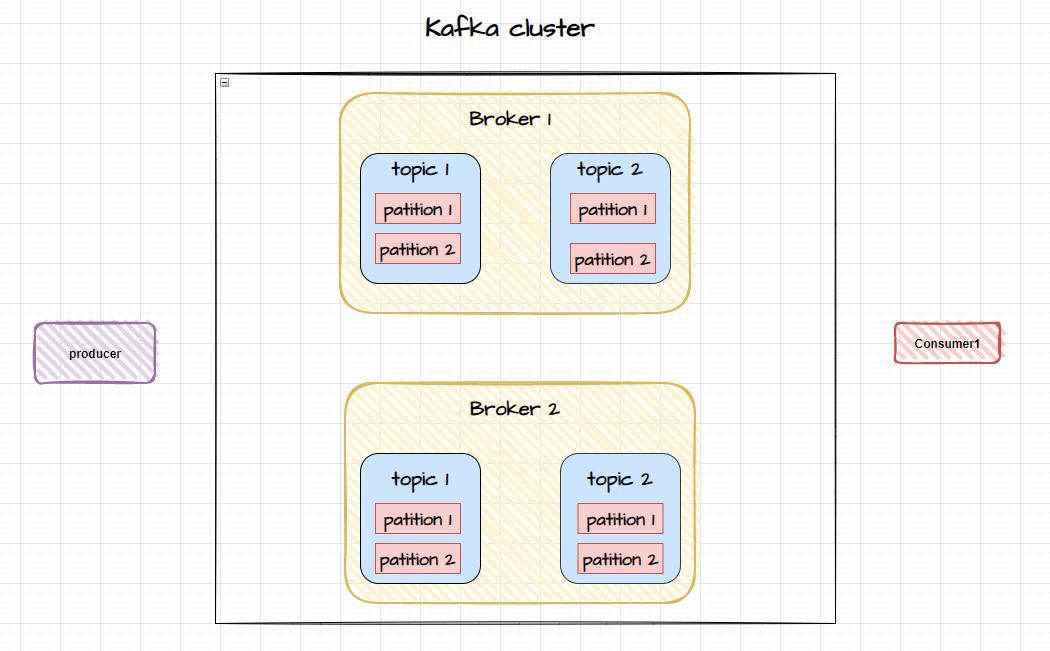
Kafka 集群如何实现数据同步
Kafka 介绍 Kafka 是一个高吞吐的分布式消息系统,不但像传统消息队列(RaabitMQ、RocketMQ等)那样能够【异步处理、流量消峰、服务解耦】 还能够把消息持久化到磁盘上,用于批量消费。除此之外由于 Kafka 被设计成分布式系统&…...
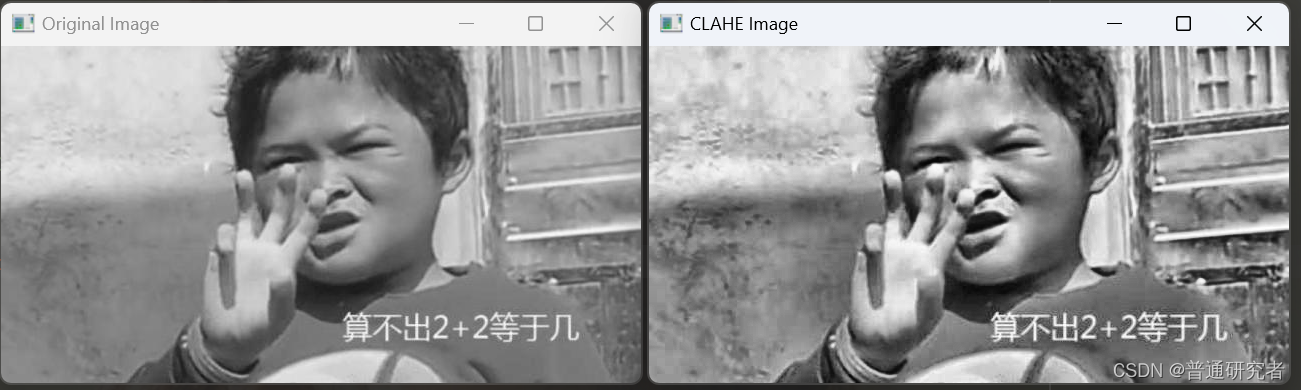
opencv- CLAHE 有限对比适应性直方图均衡化
CLAHE(Contrast Limited Adaptive Histogram Equalization)是一种对比度有限的自适应直方图均衡化技术,它能够提高图像的对比度而又避免过度增强噪声。 在OpenCV中,cv2.createCLAHE() 函数用于创建CLAHE对象,然后可以…...

IOS免签封装打包苹果APP的方法
IOS免签app封装打包苹果APP的方法如下: 准备一个未签名的IPA文件。获取一个企业证书或个人证书,用于签名IPA文件。将证书添加到Keychain Access中。安装iOS App Signer(可以在网上找到相关下载链接)。打开iOS App Signer…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
