尺度为什么是sigma?
我们先看中值滤波和均值滤波。
以前,我认为是一样的,没有区分过。
他们说,均值滤波有使图像模糊的效果。
中值滤波有使图像去椒盐的效果。为什么不同呢?试了一下,果然不同,然后追踪了一下定义。
12345,均值是3,
12345,中值也是3,这就是不加区别的原因。
再看,1,2,7,8,10;均值是?,28/5=5.6
中值显然是7。这就是区别。所以有时二者相等,有时并不同。
中值为什么能去椒盐,椒盐其实就是离谱的噪点,比如1,2,7,8,10中的1,2;其实针对均值5.6,1,10离得更远一些。
所以中值舍去的就是1,2之类,而均值舍去的是1,10之类
那么模糊又是什么意思?其实就是拉平(没有了特色和细节,就像灰色的天空,蓝色天空也行,或者整片白云,应区别噪点,比如云中飞机)了,显然5.6更合适拉平效果,而7有偏颇。
不管是拉平的平原,柏油马路的颜色,这些没有特色的,容易引起审美疲劳。一群同学中没个高个,都差不多,没几个优秀的学生,办学没特色,好中庸!图像中一团黑或白都算!
下面我们用数学公式区分一下这些不着边际的话语,平均值是这样定义的:
u=1/n*,u就是均值,xi代表上面的1,2,7,8,10;n是个数。
我们还学习了一个公式,代表偏离均值程度,sigma*sigma=1/n*。
显然值越大,偏差程度越大。
十月初,想通了一件事,就是,这两个公式是万物基础,高斯函数很牛,也是要靠这两个定义支撑。
高斯函数,在图像处理中,常常用来模糊(平滑)图像,去除噪点,那么他这个模糊和均值模糊有什么差别?
均值模糊更具有一般性,而高斯模糊更具有特殊性,为什么呢?
这个世界可以用连续和离散来概括,而均值概括了连续和离散,而高斯函数针对的是连续空间。
也就是说,均值模糊什么情况下都能用,而高斯模糊,最好在连续空间使用。
我们再看一下高斯函数的来历:
有人为了解简单的微分方程:/f(x)=c*x;
可以推导出:f(x)=K*exp(1/2*x*x*c),k是常数
欲使得:f(x)
=1;这个公式其实就是使其归一化,或者说用概率论来说,在x定义域上必然发生的概率是1,或者说必然有解。
可以推导出:c=-1/(sigma*sigma)
再利用:=
,可以推出,k=1/sigma*1/
。
所以f(x)=高斯函数;因为他是高斯发现的,故以其名字命名。
显然这些推导的成立,都是在连续的基础上。
高斯模糊,靠的就是这个sigma,这个sigma在连续函数上等于偏离均值程度,当函数不连续时,上面那个均值和偏离程度的公式仍然成立,即就是sigma*sigma=1/n*中sigma的定义包含了高斯函数中的sigma。
其实sigma的平滑模糊靠的就是这个均值u。只不过用u模糊平滑时,对x的掌控力度不如sigma好。
也有人把这个sigma叫波长,鞭长或半径,他可以达成不同的模糊程度。
最后,我们来回答,为什么这个sigma摇身一变,成为尺度了?
我在研究sift和canny以及膨胀腐蚀的时候发现,腐蚀可以认为是图像缩小,膨胀可以认为是放大,特别是腐蚀轮廓一圈,一圈消下去一个像素,sigma=0.8,膨胀一圈轮廓,一圈增加一个像素,sigma=1.2。
尺度在图像上是什么?就是放大缩小,从视觉轮廓上的膨胀腐蚀和sigma的变化,我终于想通了尺度就是sigma。
相关文章:
尺度为什么是sigma?
我们先看中值滤波和均值滤波。 以前,我认为是一样的,没有区分过。 他们说,均值滤波有使图像模糊的效果。 中值滤波有使图像去椒盐的效果。为什么不同呢?试了一下,果然不同,然后追踪了一下定义。 12345&…...

迭代器模式
自定义 Counter 结构体类型,并实现迭代器。其他语言的场景,读取数据库行数据时,使用的就是迭代器。我们使用for语言遍历数组,也是一种迭代。 结构体对象实现 Iterator trait,创建自定义的迭代器,只需要实现…...

C++ 修饰符、存储类、运算符、循环、判断
一、C修饰符类型: C允许在char、int、double数据类型前放置修饰符。 数据类型修饰符: ◆ signed:表示变量可以存储负数。对于整型变量来说,signed 可以省略,因为整型变量默认为有符号类型。 ◆ unsigned࿱…...
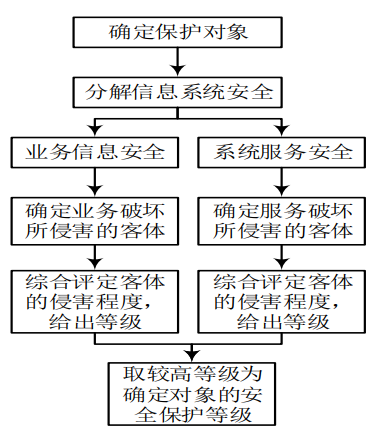
2023 hnust 湖南科技大学 信息安全管理课程 期中考试 复习资料
前言 ※老师没画重点的补充内容★往年试卷中多次出现或老师提过的,很可能考该笔记是奔着及格线去的,不是奔着90由于没有听过课,部分知识点不一定全,答案不一定完全正确 题型 试卷有很多题是原题 判断题(PPTÿ…...

N皇后问题解的个数
暴力递归 #include <stdio.h>int count0,a[15],flag; void queen(int,int); int main(){int n;scanf("%d",&n);queen(n,n);printf("%d",count); } void queen(int n,int n0){if(n<1){flag1;for(int i1;i<n0;i){for(int j1;j<n0;j){if(…...
php订单发起退款(余额和微信支付)
index.html <a class="btn btn-danger btn-change btn-tuikuan btn-disabled" href="javascript:;"><i class="fa fa-tuikuan"></i> 订单退款</a>-->order.js // 为表格绑定事件Table.api.bindevent(table);//退款…...
【SpringCloud】认识微服务、服务拆分以及远程调用
SpringCloud 1.认识微服务 1.1单体架构 单体架构:将业务的所有功能集中在一个项目中开发,打成一个包部署 单体架构的优缺点: 优点: 架构简单,部署成本低 缺点: 耦合度高(维护困难&#x…...
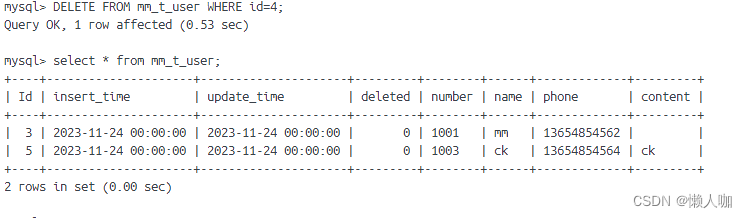
Mysql基础操作(命令行)
文章目录 Mysql基础操作(命令行)背景创建数据库选择数据库查看所有表查看表结构向表插入数据插入第一条插入第二条插入第三条 查询表数据修改表数据删除表数据 Mysql基础操作(命令行) 背景 docker安装mysql8,映射本地…...

网站遇到DDOS攻击怎么办?
最近我的网站不幸又遇到了几乎是我见到过的最大一次 DDoS 攻击,并且几乎是没有反映的时间,直接接到腾讯云的短信通知“运营商封堵”,直接造成几个小时无法访问,解封后再次遭受到大流量 DDoS 攻击,再次被“腾讯云平台封…...

中间件渗透测试-Server2131(解析+环境)
B-10:中间件渗透测试 需要环境的加qq 任务环境说明: 服务器场景:Server2131(关闭链接) 服务器场景操作系统:Linux Flag值格式:Flag{Xxxx123},括…...

探究Kafka原理-2.Kafka基本命令实操
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码、Kafka原理🔥如果感觉博主的文章还不错的话,请ὄ…...

Linux网卡没有eth0显示ens33原因以及解决办法
原因 首先说明一下eth0 与 ens33的关系: 目前的主流网卡为使用以太网络协定所开发出来的以太网卡(Ethernet),因此我们Linux就称呼这种网络接口为ethN(N为数字)。 举个栗子:就是说主机上面有一张以太网卡,因此主机的网络接口就是…...
1.前端--基本概念【2023.11.25】
1.网站与网页 网站是网页集合。 网页是网站中的一“页”,通常是 HTML 格式的文件,它要通过浏览器来阅读。 2.Web的构成 主要包括结构(Structure) 、表现(Presentation)和行为(Behaviorÿ…...

计算机视觉面试题-01
计算机视觉面试通常涉及广泛的主题,包括图像处理、深度学习、目标检测、特征提取、图像分类等。以下是一些可能在计算机视觉面试中遇到的常见问题: 图像处理和计算机视觉基础 图像是如何表示的? 图像在计算机中可以通过不同的表示方法&…...

108. 将有序数组转换为二叉搜索树 --力扣 --JAVA
题目 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。 解题思路 可以采用二分法,每次选数组中间值为…...
Springboot实现增删改差
一、包结构 二、各层代码 (1)数据User public class User {private Integer id;private String userName;private String note;public User() {super();}public User(Integer i, String userName, String note) {super();this.id i;this.userName userName;this.note note;…...
【程序员的自我修养01】编译流程概述
绪论 大家好,欢迎来到【程序员的自我修养】专栏。正如其专栏名,本专栏主要分享学习《程序员的自我修养——链接、装载与库》的知识点以及结合自己的工作经验以及思考。编译原理相关知识本身就比较有难度,我会尽自己最大的努力,争取…...
在PyCharm中正确设置Python项目
大家好,在Mac和Linux都支持Python,但许多开发者发现正确设置Python项目很困难。本文汇总了多平台中运行Python的方法,提高编程的效率,如下所示: 使用命令行运行Python。 在PyCharm(免费社区版)…...
)
scoop bucket qq脚本分析(qq绿色安装包制作)
url字段 以qq.json为例,其对应的scoop配置文件在$env:scoop\buckets\extras\bucket\qq.json 其中的url字段 "url":"https://webcdn.m.qq.com/spcmgr/download/QQ9.7.17.29230.exe#/dl.7z"为qq安装包下载地址,后缀#/dl.7z为自行添加…...
Elasticsearch:将最大内积引入 Lucene
作者:Benjamin Trent 目前,Lucene 限制 dot_product (点积) 只能在标准化向量上使用。 归一化迫使所有向量幅度等于一。 虽然在许多情况下这是可以接受的,但它可能会导致某些数据集的相关性问题。 一个典型的例子是 Cohere 构建的嵌入&#x…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
